-
1.1编委会简介
-
1.2《藏在科幻里的世界》序
-
1.3目录
-
1.4写在前面
-
1.5名家名篇·太阳火
-
1.5.12065年3月18日 北京时间PM 18∶15月球国际天文台
-
1.5.22065年3月18日 北京时间PM18∶30贵州平塘县大窝凼天文台
-
1.5.32065年3月18日 北京时间PM19∶00中学联盟天文台昌平台
-
1.5.42065年3月18日 北京时间PM19∶45月球国际天文台
-
1.5.52065年3月18日 北京时间PM20∶00中学联盟天文台昌平台
-
1.5.62065年3月18日 北京时间PM20∶20贵州平塘县大窝凼天文台
-
1.5.72065年3月18日 北京时间PM20∶40月球国际天文台
-
1.5.82065年3月18日 北京时间PM21∶00中学联盟天文台昌平台
-
1.5.92065年3月18日 北京时间PM21∶30贵州平塘县大窝凼天文台
-
1.5.102065年3月18日 北京时间PM21∶50月球国际天文台
-
1.5.112065年3月18日 北京时间PM22∶00贵州平塘县大窝凼天文台
-
1.5.122065年3月18日 北京时间PM22∶40中学联盟天文台昌平台
-
1.5.132065年3月18日 北京时间PM23∶00月球国际天文台
-
1.5.142065年3月18日 北京时间PM23∶20贵州平塘县大窝凼天文台
-
1.5.152065年3月18日 北京时间PM23∶50月球国际天文台
-
1.5.162065年3月19日 北京时间AM00∶00文昌国际宇航中心ATS计划执行部
-
1.5.172065年3月19日 北京时间AM00∶11月球国际天文台
-
1.5.182065年3月19日 北京时间AM00∶21中学联盟天文台昌平台
-
1.5.192065年3月19日 北京时间AM00∶45贵州平塘县大窝凼天文台
-
1.6宇宙探索·人类“逃离”地球奋斗史
-
1.6.1一、万户的真真假假
-
1.6.2二、眼睛“逃离”地球
-
1.6.2.1望远镜的历史
-
1.6.2.2现代望远镜的发展
-
1.6.3三、从地球到月球
-
1.6.3.1太空竞赛
-
1.6.3.2载人航天计划
-
1.6.3.3阿波罗计划
-
1.6.4四、即将离开太阳系的探测飞船们
-
1.6.4.1先驱者计划
-
1.6.4.2先驱者10号
-
1.6.4.3先驱者11号
-
1.6.4.4行星之旅计划
-
1.6.4.5水手号计划
-
1.6.4.6旅行者计划
-
1.6.4.7旅行者号后续任务
-
1.6.4.8冥王星——柯伊伯带快车
-
1.6.4.9新视野号
-
1.6.4.10新视野号现状
-
1.6.4.11即将飞出太阳系的探测器
-
1.6.4.12它们现在在哪里
-
1.6.4.13飞出太阳系?
-
1.6.4.14新视野号的金唱盘
-
1.6.5五、光速“逃离”地球时代
-
1.6.5.1飞出太阳系的“人造物”
-
1.6.6六、“逃离”地球之后一定会遇到外星人?
-
1.6.7七、等待外星人
-
1.6.8八、与外星人交流?
-
1.7微小说·剪纸
-
1.8微科普·进入高维之门
-
1.8.1超弦理论的发展
-
1.8.2寻找高维空间
-
1.8.3超弦理论里我和你一样
-
1.8.4进入高维空间
-
1.9微小说·没有敌人的战争
-
1.10微科普·文明的级别
-
1.10.1Ⅰ型文明
-
1.10.2Ⅱ级文明
-
1.10.3Ⅲ级文明
-
1.11微小说·小雷音寺
-
1.12微科普·神奇黑洞在哪里?
-
1.12.1黑洞是什么?
-
1.12.2寻找黑洞
-
1.12.3弯曲光线法
-
1.12.4星星在围着谁转圈?
-
1.12.5贪吃的家伙
-
1.12.6引力波法
-
1.12.7制造黑洞
-
1.13微小说·π
-
1.13.1零
-
1.13.2壹
-
1.13.3贰
-
1.13.4叁
-
1.14微科普·π与末日
-
1.14.1何为π
-
1.14.2π的历史
-
1.14.3π与末日
-
1.15微小说·诺亚号
-
1.16微科普·宇宙播种
-
1.16.1星光太刺眼,行星看不见
-
1.16.2天体测量法寻找行星
-
1.16.3径向速度搜星法
-
1.16.4距离是个大问题
-
1.17微小说·二次降临
-
1.17.11
-
1.17.22
-
1.17.33
-
1.17.44
-
1.18微科普·善恶外星人
-
1.18.1充满了恶意的外星人?
-
1.18.2恶意外星人盯上了地球的资源
-
1.18.3外星人防御计划
-
1.19微小说·感受
-
1.19.1一、作品
-
1.19.2二、蚁巢
-
1.19.3三、毁灭
-
1.20微科普·计算中的外星人
-
1.20.1计算外星人
-
1.20.2望而生畏的距离
-
1.20.3时间足够你撞
-
1.20.4寻找外星人
-
1.20.5没有远虑,近忧先至
-
1.21微小说·阿尔吉侬的启示录
-
1.22微科普·存储!存储?
-
1.22.1书本
-
1.22.2各种现代存储介质
-
1.22.3DNA存储
-
1.22.4等不起的DNA存储
-
1.23微小说·无限宇宙
-
1.23.14867号宇宙
-
1.23.24868号宇宙
-
1.23.34869号宇宙
-
1.23.44867号宇宙
-
1.23.54868号宇宙
-
1.23.64869号宇宙
-
1.23.74867号宇宙
-
1.23.84868号宇宙
-
1.23.94869号宇宙
-
1.23.104867号宇宙
-
1.23.114868号宇宙
-
1.23.124869号宇宙
-
1.24微科普·多重宇宙与虫洞
-
1.24.1最初的定义
-
1.24.2“泡泡”多重宇宙
-
1.24.3穿越多重宇宙
-
1.24.4假设叠假设
-
1.25微小说·给安娜的信
-
1.25.1引子
-
1.25.21
-
1.25.32
-
1.25.43
-
1.25.54
-
1.25.65
-
1.25.7尾声
-
1.26微科普·太空中的距离和时间
-
1.26.1时间会膨胀?
-
1.26.2星际旅行中的各种苦恼
-
1.26.3星际理财
-
1.26.4星际贸易
-
1.27微小说·寄生物
-
1.28微科普·寄生?寄生!
-
1.28.1真菌寄生
-
1.28.2线粒体寄生
-
1.29参考文献:
-
1.30外文文献:
1
冲出地球

 割圆术原理
割圆术原理
 π的概念图
π的概念图
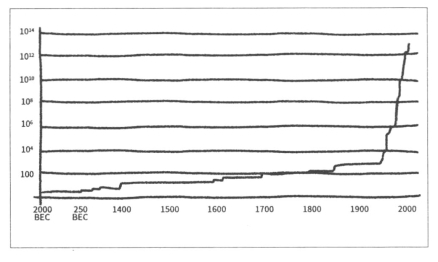
 当数学家发现新的算法、电脑变得普及后,π的精确度一直在提高
当数学家发现新的算法、电脑变得普及后,π的精确度一直在提高