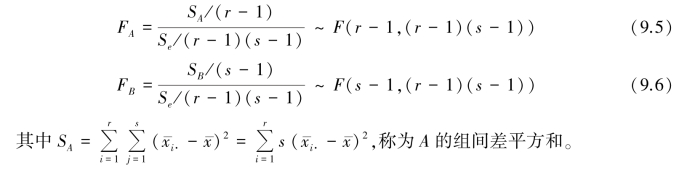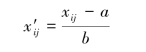社会统计学
-
1.1前言
-
1.2目录
-
1.3第1章 导 论
-
1.3.11.1 社会统计学的研究内容
-
1.3.21.2 社会统计学的研究过程
-
1.3.2.11.2.1 确定研究课题
-
1.3.2.21.2.2 探索性调查
-
1.3.2.31.2.3 理论假设的提出与概念的操作化
-
1.3.2.41.2.4 测量工具的设计
-
1.3.2.51.2.5 调查的实施
-
1.3.2.61.2.6 审核、录入与录入误差的消除
-
1.3.2.71.2.7 统计分析与理论假设的检验
-
1.3.31.3 统计分析方法在社会学研究中的作用
-
1.3.3.11.3.1 统计分析方法应用水平是社会学研究科学性的重要标志
-
1.3.3.21.3.2 统计分析方法是发现和彰显统计规律的有效工具
-
1.3.41.4 统计学在研究过程中的地位
-
1.3.51.5 变量的层次及统计分析方法的选择
-
1.3.5.11.5.1 变量的层次
-
1.3.5.21.5.2 统计分析方法的选择
-
1.3.6【习 题】
-
1.4第2章 社会调查与数据处理
-
1.4.12.1 社会调查研究的类型
-
1.4.1.12.1.1 按研究的目的分
-
1.4.1.22.1.2 按研究的时间维度分
-
1.4.22.2 社会调查研究流程
-
1.4.2.12.2.1 选择研究问题
-
1.4.2.22.2.2 研究设计
-
1.4.2.32.2.3 收集资料
-
1.4.2.42.2.4 资料整理与分析
-
1.4.2.52.2.5 撰写研究报告
-
1.4.32.3 社会调查资料的特点
-
1.4.3.12.3.1 随机性
-
1.4.3.22.3.2 统计规律性
-
1.4.42.4 问卷调查资料的整理
-
1.4.4.12.4.1 问卷调查资料的审核
-
1.4.4.22.4.2 问卷资料的编码
-
1.4.4.32.4.3 编码的原则
-
1.4.4.42.4.4 特殊类型客观题的编码
-
1.4.4.52.4.5 数据录入
-
1.4.5【习 题】
-
1.5第3章 单变量的描述统计分析
-
1.5.13.1 单变量的分布及其描述方法
-
1.5.1.13.1.1 变量及其分布
-
1.5.1.23.1.2 统计表
-
1.5.1.33.1.3 统计图
-
1.5.23.2 集中趋势
-
1.5.2.13.2.1 众数
-
1.5.2.23.2.2 中位数
-
1.5.2.33.2.3 算术平均值
-
1.5.2.43.2.4 众数、中位数和算术平均值的比较
-
1.5.33.3 离散趋势
-
1.5.3.13.3.1 异众比率
-
1.5.3.23.3.2 极差(全距)
-
1.5.3.33.3.3 四分位差
-
1.5.3.43.3.4 方差与标准差
-
1.5.4【习 题】
-
1.6第4章 两个类别变量关系的描述统计
-
1.6.14.1 列联表分析
-
1.6.1.14.1.1 两个类别变量相关的概念
-
1.6.1.24.1.2 列联表的结构
-
1.6.1.34.1.3 列联表的种类
-
1.6.1.44.1.4 列联表中的分布
-
1.6.1.54.1.5 列联表中变量的相互独立性
-
1.6.24.2 分类图
-
1.6.2.14.2.1 分类条形图
-
1.6.2.24.2.2 分类饼图
-
1.6.2.34.2.3 折线图
-
1.6.34.3 列联相关系数
-
1.6.3.14.3.1 消减误差比例的统计思想
-
1.6.3.24.3.2 λ 系数
-
1.6.3.34.3.3 系数
-
1.6.44.4 等级相关系数
-
1.6.4.14.4.1 等级相关的概念
-
1.6.4.24.4.2 斯皮尔曼等级相关系数rs
-
1.6.4.34.4.3 Gamma 等级相关系数
-
1.6.4.44.4.4 肯德尔系数
-
1.6.4.54.4.5 Somer’s d 系数
-
1.6.5【习 题】
-
1.7第5章 两个尺度变量关系的描述统计
-
1.7.15.1 相关分析
-
1.7.1.15.1.1 相关的概念
-
1.7.1.25.1.2 散点图
-
1.7.1.35.1.3 相关系数
-
1.7.25.2 回归分析
-
1.7.2.15.2.1 回归分析的统计思想
-
1.7.2.25.2.2 线性回归
-
1.7.2.35.2.3 非线性回归
-
1.7.2.45.2.4 回归分析的应用
-
1.7.35.3 相关与回归的比较
-
1.7.4【习 题】
-
1.8第6章 类别变量与尺度变量关系的描述统计
-
1.8.16.1 平均值比较分析
-
1.8.1.16.1.1 平均值比较分析的统计思想
-
1.8.1.26.1.2 统计表、条形图与折线图
-
1.8.26.2 相关比率
-
1.8.2.16.2.1 相关比率的构建思想
-
1.8.2.26.2.2 相关比率的计算
-
1.8.3【习 题】
-
1.9第7章 参数估计
-
1.9.17.1 参数估计的基本原理
-
1.9.1.17.1.1 估计量与估计值
-
1.9.1.27.1.2 点估计与区间估计
-
1.9.1.37.1.3 评价估计量的标准
-
1.9.27.2 一个总体参数的区间估计
-
1.9.2.17.2.1 单正态总体、方差已知,或非正态总体、大样本
-
1.9.2.27.2.2 正态总体、方差未知、小样本
-
1.9.37.3 两个总体参数的区间估计
-
1.9.3.17.3.1 双正态总体均值之差的置信区间估计
-
1.9.3.27.3.2 两个总体方差比的区间估计
-
1.9.47.4 样本量的确定
-
1.9.4.17.4.1 估计总体均值时样本量的确定
-
1.9.4.27.4.2 估计总体比例时样本量的确定
-
1.9.5【习 题】
-
1.10第8章 假设检验
-
1.10.18.1 假设检验的基本概念与原理
-
1.10.1.18.1.1 假设检验的基本原理与概念
-
1.10.1.28.1.2 假设检验的一般步骤
-
1.10.1.38.1.3 假设检验的两类错误
-
1.10.1.48.1.4 双侧假设检验与单侧假设检验
-
1.10.28.2 正态总体均值与方差的假设检验
-
1.10.2.18.2.1 单个总体N(μ,σ2)均值μ 与方差σ2 的检验
-
1.10.2.28.2.2 两个正态总体均值与方差的检验
-
1.10.2.38.2.3 基于成对数据的检验(t 检验)
-
1.10.2.48.2.4 区间估计与假设检验的关系
-
1.10.38.3 非正态总体参数的假设检验
-
1.10.3.18.3.1 概率p 的假设检验
-
1.10.3.28.3.2 非正态总体均值的大样本检验
-
1.10.48.4 应用案例
-
1.10.4.18.4.1 硝化棉含水量的检验
-
1.10.4.28.4.2 评委打分中为什么要去掉最高分和最低分
-
1.10.5【习 题】
-
1.11第9章 方差分析
-
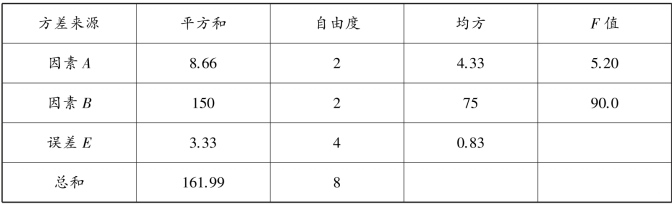
1.11.19.1 一元方差分析
-
1.11.1.19.1.1 基本概念
-
1.11.1.29.1.2 分析步骤
-
1.11.29.2 二元方差分析
-
1.11.2.19.2.1 双因素方差分析
-
1.11.2.29.2.2 理想的独立模型——无交互作用的双因素方差分析
-
1.11.2.39.2.3 有交互作用的双因素方差分析
-
1.11.3【习 题】
-
1.12第10章 多元线性回归
-
1.12.110.1 回归研究的对象
-
1.12.1.110.1.1 回归是研究定距变量与定距变量之间的非确定关系的
-
1.12.1.210.1.2 多元线性回归的假设
-
1.12.1.310.1.3 多元回归模型与回归方程
-
1.12.1.410.1.4 确定性关系与非确定性关系
-
1.12.1.510.1.5 多元回归系数的估计——最小二乘法
-
1.12.1.610.1.6 最小二乘法(OLS)估计量的性质
-
1.12.210.2 多元回归方程的拟合优度
-
1.12.2.110.2.1 多元判定系数R2 与复相关系数R
-
1.12.2.210.2.2 R2 与矫正R2
-
1.12.310.3 显著性检验
-
1.12.3.110.3.1 回归方程的总体显著性检验
-
1.12.3.210.3.2 关于偏回归系数的假设检验
-
1.12.410.4 多重共线性
-
1.12.4.110.4.1 多重共线性的定义
-
1.12.4.210.4.2 多重共线性导致的可能结果
-
1.12.4.310.4.3 多重共线性的判别与处理
-
1.12.510.5 用回归方程进行预测
-
1.12.6【习 题】
-
1.13第11章 时间序列分析
-
1.13.111.1 时间序列及平稳性与检验
-
1.13.1.111.1.1 时间序列的定义
-
1.13.1.211.1.2 平稳时间序列与非平稳随机序列
-
1.13.1.311.1.3 平稳性数字特征
-
1.13.211.2 平稳时间序列的统计性质
-
1.13.2.111.2.1 平稳时间序列统计性质
-
1.13.2.211.2.2 平稳时间序列的意义
-
1.13.2.311.2.3 平稳性的检验
-
1.13.311.3 纯随机性检验
-
1.13.3.111.3.1 纯随机序列的定义
-
1.13.3.211.3.2 白噪声序列的性质
-
1.13.3.311.3.3 纯随机性检验
-
1.13.411.4 时间序列预测的步骤
-
1.13.4.111.4.1 平稳序列的预测
-
1.13.4.211.4.2 非平稳时间序列数据预测
-
1.13.5【习 题】
-
1.14附 录
-
1.15参考文献