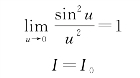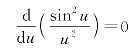-
1.1前言
-
1.2目录
-
1.3第一章 光的干涉
-
1.3.1第一节 光波
-
1.3.1.1一、光是一种电磁波
-
1.3.1.2二、光波的数学表达式
-
1.3.1.3三、原子发光机理
-
1.3.2第二节 光波的叠加
-
1.3.2.1一、光波的叠加
-
1.3.2.2二、光程和光程差
-
1.3.3第三节 干涉现象和相干条件
-
1.3.3.1一、相干条件
-
1.3.3.2二、干涉条纹的可见度
-
1.3.4第四节 分波面法产生的干涉
-
1.3.4.1一、杨氏双缝实验
-
1.3.4.2二、菲涅耳双平面镜
-
1.3.4.3三、洛埃镜
-
1.3.5第五节 光场的时间相干性和空间相干性
-
1.3.5.1一、光场的时间相干性
-
1.3.5.2二、光场的空间相干性
-
1.3.6第六节 分振幅法产生的干涉
-
1.3.6.1一、薄膜干涉的光程差
-
1.3.6.2二、等倾干涉
-
1.3.6.3三、等厚干涉
-
1.3.7第七节 劈尖 牛顿环
-
1.3.7.1一、劈尖的干涉
-
1.3.7.2二、牛顿环
-
1.3.7.3三、薄膜干涉的一些应用
-
1.3.8第八节 迈克尔逊干涉仪
-
1.3.9习题
-
1.4第二章 光的衍射
-
1.4.1第一节 光的衍射现象
-
1.4.2第二节 惠更斯-菲涅耳原理
-
1.4.3第三节 菲涅耳衍射
-
1.4.3.1一、菲涅耳半波带法
-
1.4.3.2二、菲涅耳圆孔衍射
-
1.4.3.3三、菲涅耳圆屏衍射
-
1.4.4第四节 夫琅和费单缝衍射
-
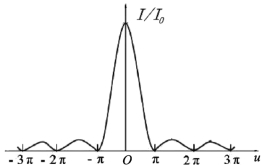
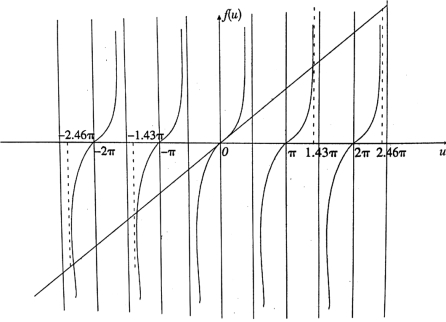
1.4.4.1一、实验装置和光强分布公式推导
-
1.4.4.2二、衍射花样
-
1.4.5第五节 夫琅和费圆孔衍射
-
1.4.6第六节 光学系统的分辨本领
-
1.4.7第七节 衍射光栅
-
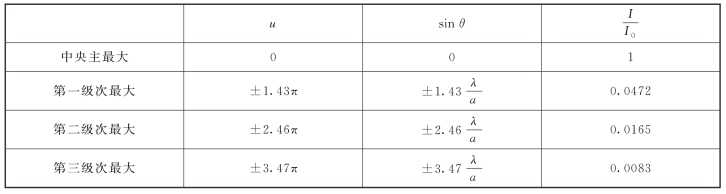
1.4.7.1一、光强分布公式
-
1.4.7.2二、衍射花样
-
1.4.7.3三、光栅方程
-
1.4.7.4四、光栅光谱
-
1.4.7.5五、光栅的色散本领和色分辨本领
-
1.4.8第八节 晶体对X射线的衍射
-
1.4.9习题
-
1.5第三章 光的偏振
-
1.5.1第一节 自然光与偏振光
-
1.5.2第二节 偏振片
-
1.5.3第三节 光在反射和折射时的偏振
-
1.5.3.1一、反射时的偏振现象
-
1.5.3.2二、折射时的偏振现象
-
1.5.4第四节 光通过各向异性晶体时的双折射现象
-
1.5.4.1一、双折射
-
1.5.4.2二、光轴与主截面
-
1.5.4.3三、o光和e光的相对光强度
-
1.5.4.4四、单轴晶体内o光与e光的波阵面
-
1.5.4.5五、单轴晶体内o光与e光的传播
-
1.5.5第五节 偏振棱镜
-
1.5.5.1一、尼科耳棱镜
-
1.5.5.2二、渥拉斯顿棱镜
-
1.5.6第六节 椭圆偏振光
-
1.5.6.1一、椭圆偏振光的产生
-
1.5.6.2二、波片
-
1.5.6.3三、圆偏振光和椭圆偏振光的检定
-
1.5.7第七节 偏振光的干涉
-
1.5.8第八节 旋光现象
-
1.5.9习题
-
1.6第四章 几何光学的基本原理
-
1.6.1第一节 几何光学的基本定律
-
1.6.2第二节 费马原理
-
1.6.3第三节 全反射
-
1.6.4第四节 棱镜
-
1.6.5第五节 有关成像问题的基本概念
-
1.6.6第六节 光在平面上的反射和折射
-
1.6.6.1一、光在平面上的反射
-
1.6.6.2二、光在平面上的折射
-
1.6.7第七节 光在球面上的折射和反射
-
1.6.7.1一、符号法则
-
1.6.7.2二、光在球面上的折射
-
1.6.7.3三、光在球面上的反射
-
1.6.8第八节 近轴物体经球面折射和反射成像
-
1.6.8.1一、近轴物体经球面折射成像
-
1.6.8.2二、近轴物体经球面反射成像
-
1.6.9第九节 透镜
-
1.6.9.1一、厚透镜成像
-
1.6.9.2二、薄透镜成像公式
-
1.6.9.3三、薄透镜作图求像法
-
1.6.10第十节 共轴光具组的基点基面
-
1.6.10.1一、焦点和焦平面
-
1.6.10.2二、主点和主平面
-
1.6.10.3三、节点
-
1.6.11第十一节 共轴光具组的成像
-
1.6.11.1一、共轴光具组的作图求像法
-
1.6.11.2二、光具组的物像公式
-
1.6.12习题
-
1.7第五章 光学仪器的基本原理
-
1.7.1第一节 眼睛
-
1.7.1.1一、人眼的结构和调节
-
1.7.1.2二、非正常眼的矫正
-
1.7.2第二节 助视仪器的放大率
-
1.7.3第三节 放大镜 目镜
-
1.7.3.1一、放大镜
-
1.7.3.2二、目镜
-
1.7.4第四节 显微镜
-
1.7.5第五节 望远镜
-
1.7.5.1一、天文望远镜
-
1.7.5.2二、伽利略望远镜
-
1.7.6第六节 光度学基础
-
1.7.6.1一、辐射通量
-
1.7.6.2二、视见函数
-
1.7.6.3三、光通量
-
1.7.6.4四、发光强度
-
1.7.6.5五、照度
-
1.7.6.6六、亮度
-
1.7.7习题
-
1.8第六章 光与物质的相互作用
-
1.8.1第一节 光的吸收
-
1.8.1.1一、光的吸收定律
-
1.8.1.2二、一般吸收和选择吸收
-
1.8.1.3三、吸收光谱
-
1.8.2第二节 光的散射
-
1.8.2.1一、瑞利散射
-
1.8.2.2二、米氏散射
-
1.8.2.3三、拉曼散射
-
1.8.2.4四、布里渊散射
-
1.8.3第三节 光的色散
-
1.8.3.1一、光的色散
-
1.8.3.2二、正常色散
-
1.8.3.3三、反常色散
-
1.8.3.4四、色散观察
-
1.8.4习题
-
1.9第七章 光的量子性
-
1.9.1第一节 热辐射 基尔霍夫辐射定律
-
1.9.1.1一、热辐射
-
1.9.1.2二、基尔霍夫辐射定律
-
1.9.2第二节 黑体及黑体辐射实验定律
-
1.9.2.1一、黑体
-
1.9.2.2二、绝对黑体的辐射实验定律
-
1.9.3第三节 普朗克公式 能量子
-
1.9.3.1一、维恩公式和瑞利-金斯公式
-
1.9.3.2二、普朗克公式与能量子假设
-
1.9.4第四节 光电效应
-
1.9.4.1一、光电效应实验装置
-
1.9.4.2二、光电效应的实验规律
-
1.9.4.3三、光电效应与光的波动论的矛盾
-
1.9.4.4四、爱因斯坦假说
-
1.9.4.5五、爱因斯坦光电效应方程
-
1.9.4.6六、爱因斯坦方程对光电效应实验规律的解释
-
1.9.5第五节 康普顿效应
-
1.9.5.1一、康普顿效应的实验规律
-
1.9.6第六节 光的波粒二象性
-
1.9.6.1一、光的波粒二象性
-
1.9.6.2二、实物粒子的波粒二象性
-
1.9.7习题
-
1.10第八章 激光
-
1.10.1第一节 光的吸收与辐射
-
1.10.2第二节 产生激光的条件
-
1.10.2.1一、粒子数反转
-
1.10.2.2二、光学谐振腔
-
1.10.3第三节 红宝石激光器
-
1.10.4第四节 氦氖激光器
-
1.10.5第五节 激光的特点和应用
-
1.10.5.1一、方向性好
-
1.10.5.2二、高亮度
-
1.10.5.3三、单色性好
-
1.10.5.4四、相干性好
-
1.10.6第六节 全息照相
-
1.10.7习题
1
光学教程