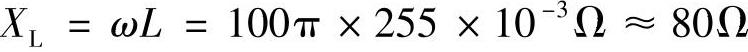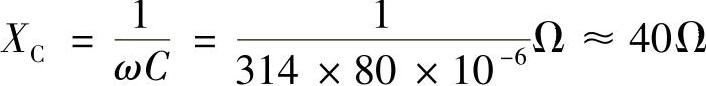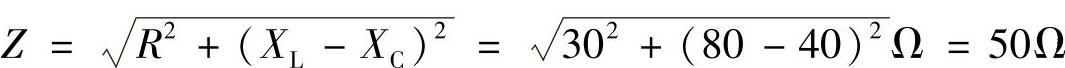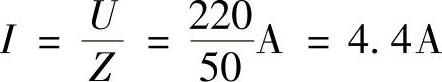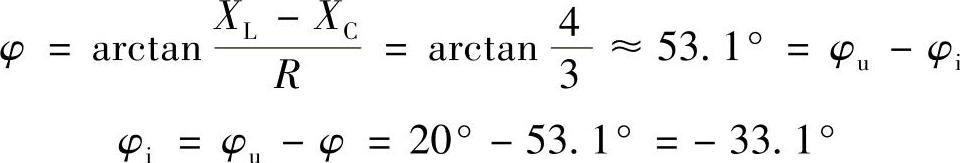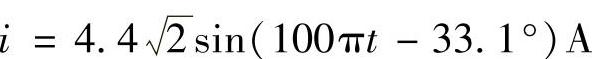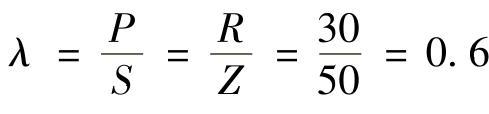-
1.1前言
-
1.2目录
-
1.3单元一 直流电路基础知识
-
1.3.1第一节 库仑定律
-
1.3.1.1一、电荷
-
1.3.1.2二、库仑定律的内容及其应用
-
1.3.1.3课后练习
-
1.3.2第二节 电场和电场强度
-
1.3.2.1一、电场
-
1.3.2.2二、电场强度
-
1.3.2.3三、电力线
-
1.3.2.4课后练习
-
1.3.3第三节 电流
-
1.3.3.1一、电流的认识
-
1.3.3.2二、电流形成的条件
-
1.3.3.3三、电流的大小
-
1.3.3.4四、电流的方向
-
1.3.3.5五、直流电流的测量
-
1.3.3.6课后练习
-
1.3.4第四节 电压和电位
-
1.3.4.1一、电场对电荷的做功
-
1.3.4.2二、电压
-
1.3.4.3三、电位
-
1.3.4.4四、电压的方向
-
1.3.4.5五、电压的测量
-
1.3.4.6六、常见的几种电压值
-
1.3.4.7课后练习
-
1.3.5第五节 电源和电动势
-
1.3.5.1一、电源
-
1.3.5.2二、电源电动势
-
1.3.5.3课后练习
-
1.3.6第六节 电阻和电阻定律
-
1.3.6.1一、电阻
-
1.3.6.2二、电阻定律
-
1.3.6.3三、电阻器
-
1.3.6.4四、用万用表测量电阻
-
1.3.6.5课后练习
-
1.3.7第七节 电路和欧姆定律
-
1.3.7.1一、电路
-
1.3.7.2二、欧姆定律
-
1.3.7.3三、电源的外特性
-
1.3.7.4课后练习
-
1.3.8第八节 电能和电功率
-
1.3.8.1一、电能
-
1.3.8.2二、电功率
-
1.3.8.3三、电气设备的额定值
-
1.3.8.4四、电流的热效应
-
1.3.8.5五、电路中的功率平衡
-
1.3.8.6课后练习
-
1.3.9第九节 电源的最大输出功率
-
1.3.9.1课后练习
-
1.3.10本单元知识要点
-
1.3.10.1一、电场
-
1.3.10.2二、电路
-
1.3.10.3三、常用物理量
-
1.3.10.4四、定律和定理
-
1.3.11知识能力自测题
-
1.3.11.1一、填空题
-
1.3.11.2二、选择题
-
1.3.11.3三、计算题
-
1.3.11.4四、实验题
-
1.4单元二 直流电路
-
1.4.1第一节 电阻串联电路
-
1.4.1.1一、电阻串联电路的定义
-
1.4.1.2二、电阻串联电路的特点
-
1.4.1.3三、电阻串联电路的应用
-
1.4.1.4课后练习
-
1.4.2第二节 电阻并联电路
-
1.4.2.1一、电阻并联电路的定义
-
1.4.2.2二、电阻并联电路的特点
-
1.4.2.3三、电阻并联电路的应用
-
1.4.2.4课后练习
-
1.4.3第三节 电阻混联电路
-
1.4.3.1课后练习
-
1.4.4第四节 电池的连接
-
1.4.4.1一、电池的串联
-
1.4.4.2二、电池的并联
-
1.4.4.3三、电池的混联
-
1.4.4.4课后练习
-
1.4.5第五节 电路中各点电位的计算
-
1.4.5.1一、电位参考点的选择
-
1.4.5.2二、计算电路中某点电位的方法和步骤
-
1.4.5.3三、利用电位概念简化电路的画法
-
1.4.5.4课后练习
-
1.4.6第六节 基尔霍夫定律
-
1.4.6.1一、复杂电路中的几个名词
-
1.4.6.2二、基尔霍夫定律的内容
-
1.4.6.3课后练习
-
1.4.7第七节 支路电流法
-
1.4.7.1一、支路电流法的定义
-
1.4.7.2二、支路电流法解题步骤
-
1.4.7.3课后练习
-
1.4.8第八节 电压源与电流源及其等效变换
-
1.4.8.1一、电压源
-
1.4.8.2二、电流源
-
1.4.8.3三、两种实际电源模型之间的等效变换
-
1.4.8.4课后练习
-
1.4.9第九节 戴维南定理
-
1.4.9.1一、二端网络的有关概念
-
1.4.9.2二、戴维南定理的内容
-
1.4.9.3课后练习
-
1.4.10第十节 叠加定理
-
1.4.10.1一、叠加定理的内容
-
1.4.10.2二、叠加定理应注意的问题
-
1.4.10.3课后练习
-
1.4.11本单元知识要点
-
1.4.11.1一、电阻串、并联电路
-
1.4.11.2二、电池的连接
-
1.4.11.3三、电路中各点电位的计算
-
1.4.11.4四、基尔霍夫定律
-
1.4.11.5五、支路电流法
-
1.4.11.6六、电压源与电流源及其等效变换
-
1.4.11.7七、戴维南定理
-
1.4.11.8八、叠加定理
-
1.4.12知识能力自测题
-
1.4.12.1一、填空题
-
1.4.12.2二、选择题
-
1.4.12.3三、计算题
-
1.4.12.4四、实验题
-
1.5单元三 电容器
-
1.5.1第一节 电容器与电容
-
1.5.1.1一、电容器
-
1.5.1.2二、电容
-
1.5.1.3三、平行板电容器
-
1.5.1.4课后练习
-
1.5.2第二节 电容器的参数和种类
-
1.5.2.1一、电容器的参数
-
1.5.2.2二、电容器的种类
-
1.5.2.3课后练习
-
1.5.3第三节 电容器的连接
-
1.5.3.1一、电容器的串联
-
1.5.3.2二、电容器的并联
-
1.5.3.3课后练习
-
1.5.4第四节 电容器中的电场能
-
1.5.4.1一、电容器的充电和放电
-
1.5.4.2二、电容器质量的判别
-
1.5.4.3三、电容器中的电场能
-
1.5.4.4课后练习
-
1.5.5本单元知识要点
-
1.5.5.11.电容器与电容
-
1.5.5.22.电容器的参数和种类
-
1.5.5.33.电容器的连接
-
1.5.5.44.电容器中的电场能
-
1.5.6知识能力自测题
-
1.5.6.1一、判断题
-
1.5.6.2二、填空题
-
1.5.6.3三、选择题
-
1.5.6.4四、计算题
-
1.6单元四 磁与电磁感应
-
1.6.1第一节 磁感应强度与磁通
-
1.6.1.1一、磁体、磁极、磁场和磁感线
-
1.6.1.2二、电流的磁效应
-
1.6.1.3三、磁感应强度与磁通的内容
-
1.6.1.4课后练习
-
1.6.2第二节 磁场强度
-
1.6.2.1一、磁导率
-
1.6.2.2二、磁场强度的内容
-
1.6.2.3三、几种常见载流导体的磁场强度
-
1.6.2.4课后练习
-
1.6.3第三节 铁磁性物质的磁化
-
1.6.3.1一、铁磁性物质的磁化知识
-
1.6.3.2二、磁化曲线
-
1.6.3.3三、磁滞回线
-
1.6.3.4四、铁磁材料的分类
-
1.6.3.5五、磁化和退磁方法
-
1.6.3.6课后练习
-
1.6.4第四节 磁场对电流的作用
-
1.6.4.1一、磁场对载流直导体的作用力
-
1.6.4.2二、磁场对通电矩形线圈的力矩
-
1.6.4.3三、磁场对运动电荷的作用力
-
1.6.4.4课后练习
-
1.6.5第五节 电磁感应现象
-
1.6.5.1一、电磁感应实验
-
1.6.5.2二、产生感应电流的条件
-
1.6.5.3三、感应电流的方向
-
1.6.5.4课后练习
-
1.6.6第六节 电磁感应定律
-
1.6.6.1一、产生感应电动势的一般条件
-
1.6.6.2二、感应电动势的大小
-
1.6.6.3三、感应电流的大小
-
1.6.6.4课后练习
-
1.6.7第七节 电感器
-
1.6.7.1课后练习
-
1.6.8第八节 自感与互感
-
1.6.8.1一、自感
-
1.6.8.2二、互感
-
1.6.8.3三、涡流
-
1.6.8.4课后练习
-
1.6.9第九节 互感线圈的同名端
-
1.6.9.1一、同名端
-
1.6.9.2二、同名端的判定方法
-
1.6.9.3课后练习
-
1.6.10第十节 线圈中的磁场能
-
1.6.10.1课后练习
-
1.6.11本单元知识要点
-
1.6.11.11.基本物理量(表4-3)
-
1.6.11.22.电流的磁效应
-
1.6.11.33.铁磁性物质的磁化
-
1.6.11.44.磁场对电流的作用
-
1.6.11.55.电磁感应
-
1.6.11.66.电感器
-
1.6.11.77.自感和自感电动势
-
1.6.11.88.互感线圈的同名端
-
1.6.11.99.线圈中的磁场能
-
1.6.12知识能力自测题
-
1.6.12.1一、填充题
-
1.6.12.2二、选择题
-
1.6.12.3三、计算题
-
1.7单元五 正弦交流电路
-
1.7.1第一节 正弦交流电的基础知识
-
1.7.1.1一、正弦交流电的产生
-
1.7.1.2二、正弦交流电的周期、频率和角频率
-
1.7.1.3三、正弦交流电的相位和相位差
-
1.7.1.4四、正弦交流电的瞬时值、最大值和有效值
-
1.7.1.5五、正弦交流电的三要素
-
1.7.1.6课后练习
-
1.7.2第二节 旋转矢量
-
1.7.2.1一、解析式
-
1.7.2.2二、波形图
-
1.7.2.3三、旋转矢量的内容
-
1.7.2.4课后练习
-
1.7.3第三节 纯电阻电路
-
1.7.3.1一、电流和电压的数量关系
-
1.7.3.2二、电流和电压的相位关系
-
1.7.3.3三、纯电阻交流电路的功率
-
1.7.3.4课后练习
-
1.7.4第四节 纯电感电路
-
1.7.4.1一、电流和电压的数量关系
-
1.7.4.2二、电流和电压的相位关系
-
1.7.4.3三、纯电感交流电路的功率
-
1.7.4.4课后练习
-
1.7.5第五节 纯电容电路
-
1.7.5.1一、电流和电压的数量关系
-
1.7.5.2二、电流和电压的相位关系
-
1.7.5.3三、纯电容交流电路的功率
-
1.7.5.4课后练习
-
1.7.6第六节 RL串联电路
-
1.7.6.1一、RL串联电路电压间的关系
-
1.7.6.2二、RL串联电路的阻抗
-
1.7.6.3三、RL串联电路的功率
-
1.7.6.4课后练习
-
1.7.7第七节 RC串联电路
-
1.7.7.1一、RC串联电路电压间的关系
-
1.7.7.2二、RC串联电路的阻抗
-
1.7.7.3三、RC串联电路的功率
-
1.7.7.4课后练习
-
1.7.8第八节 RLC串联电路
-
1.7.8.1一、RLC串联电路电压间的关系
-
1.7.8.2二、RLC串联电路的阻抗
-
1.7.8.3三、RLC串联电路的功率
-
1.7.8.4课后练习
-
1.7.9第九节 RLC串联谐振电路
-
1.7.9.1一、谐振条件与谐振频率
-
1.7.9.2二、谐振参数
-
1.7.9.3三、谐振特点
-
1.7.9.4四、串联谐振电路的选择性和通频带
-
1.7.9.5五、调谐原理
-
1.7.9.6课后练习
-
1.7.10第十节 RLC并联电路
-
1.7.10.1一、RLC并联电路知识
-
1.7.10.2二、RLC并联谐振电路
-
1.7.10.3课后练习
-
1.7.11第十一节 实际线圈与电容并联电路
-
1.7.11.1课后练习
-
1.7.12第十二节 提高功率因数的意义和方法
-
1.7.12.1一、提高功率因数的意义
-
1.7.12.2二、提高功率因数的方法
-
1.7.12.3课后练习
-
1.7.13本单元知识要点
-
1.7.13.1一、R、L、C纯电路
-
1.7.13.2二、RLC串、并联电路
-
1.7.13.3三、RLC串、并联谐振电路
-
1.7.13.4四、提高功率因数的方法
-
1.7.14知识能力自测题
-
1.7.14.1一、填空题
-
1.7.14.2二、计算题
-
1.8单元六 三相交流电路
-
1.8.1第一节 三相交流电源
-
1.8.1.1一、三相交流电动势的产生
-
1.8.1.2二、相序
-
1.8.1.3三、三相电源的连接
-
1.8.1.4四、相电压和线电压
-
1.8.1.5课后练习
-
1.8.2第二节 三相负载的连接
-
1.8.2.1一、连接方式
-
1.8.2.2二、符号和规定
-
1.8.2.3三、电路计算
-
1.8.2.4课后练习
-
1.8.3第三节 三相交流电路的功率
-
1.8.3.1课后练习
-
1.8.4第四节 安全用电
-
1.8.4.1一、触电与救护
-
1.8.4.2二、防止触电的技术措施
-
1.8.4.3三、采用各种安全保护用具
-
1.8.4.4课后练习
-
1.8.5本单元知识要点
-
1.8.5.1一、三相交流电源
-
1.8.5.2二、三相负载的接法
-
1.8.5.3三、三相电路的功率
-
1.8.5.4四、安全用电
-
1.8.6知识能力自测题
-
1.8.6.1一、填空题
-
1.8.6.2二、选择题
-
1.8.6.3三、计算题
-
1.8.6.4四、回答问题
-
1.9单元七 变压器和交流电动机
-
1.9.1第一节 变压器
-
1.9.1.1一、变压器的构造和分类
-
1.9.1.2二、变压器的工作原理
-
1.9.1.3三、变压器的功率和效率
-
1.9.1.4四、变压器的铭牌和额定值
-
1.9.1.5课后练习
-
1.9.2第二节 交流电动机
-
1.9.2.1一、三相笼型异步电动机的构造
-
1.9.2.2二、三相异步电动机的工作原理
-
1.9.2.3三、三相异步电动机的控制
-
1.9.2.4四、三相异步电动机的铭牌数据
-
1.9.2.5课后练习
-
1.9.3本单元知识要点
-
1.9.3.1一、变压器
-
1.9.3.2二、交流电动机
-
1.9.4知识能力自测题
-
1.9.4.1一、填空题
-
1.9.4.2二、判断题
-
1.9.4.3三、选择题
-
1.9.4.4四、计算题
-
1.10参考答案
-
1.10.1单元一 直流电路基础知识
-
1.10.2单元二 直流电路
-
1.10.3单元三 电容器
-
1.10.4单元四 磁与电磁感应
-
1.10.5单元五 正弦交流电路
-
1.10.6单元六 三相交流电路
-
1.10.7单元七 变压器和交流电动机
-
1.11参考文献
1
电工基础
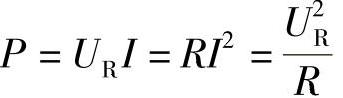
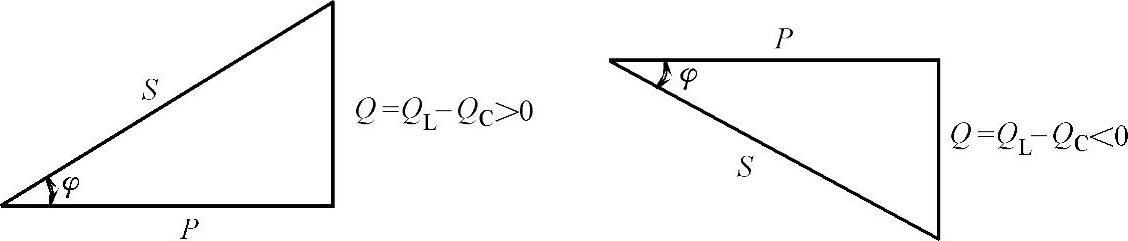

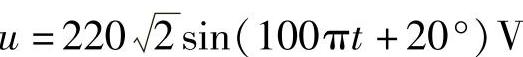 的电源上,求:
的电源上,求: