不定方程的概率解法

结论：

(1) 方程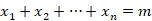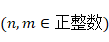， 的正整数解共有 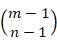个；

(2) 方程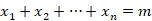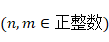， 的非负整数解共有 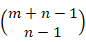个；

问题：(原文出处：https://blog.csdn.net/u012074597/article/details/79702140)

先从一个问题引入：假如一个湖里有4种鱼，而我总共钓上来了10条鱼，请问鱼的组合共有多少种可能？（注意这个问题里某种鱼的条数可以为0）。

更一般地，我们可以假设有n种鱼，且一共钓到了 m条，那可能的结果数就是满足：

，

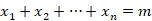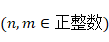
的非负整数向量 (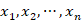) 的个数。

生活中经常会碰到类似的问题，所以就称呼为“不定方程非负整数解个数”问题。

解法：

要计算非负整数向量的个数，我们可以先考虑正整数向量(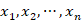)的个数。我们假设有m个连续的数值1排成一行：

111⋯11

注意，总共有m-1个间隔，我们需要将n-1个加号放到这些间隔中。例如，如果m=8，n=3，那么选择

1+1111+111

对应解。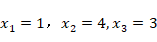

故结论(1)成立。

为了得到非负整数解（而不是正整数解）的个数，注意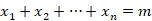，的非负整数解个数与

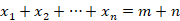
的正整数解个数是相同的（令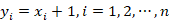）。因此得到结论(2)

所以回到最开始的问题，总共有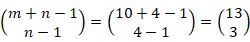=286中可能的情况。