正态分布与幂律分布
https://shanguangyu.com/articles/distribution/
在我们的日常生活中,总是会被各式各样的现象所包围,小到人们的身高分布,大到国家的财富分布。久而久之,人们抽象出了两个通用的模型来解释这些现象,一个叫做正态分布,另一个叫做幂律分布。
#正态分布
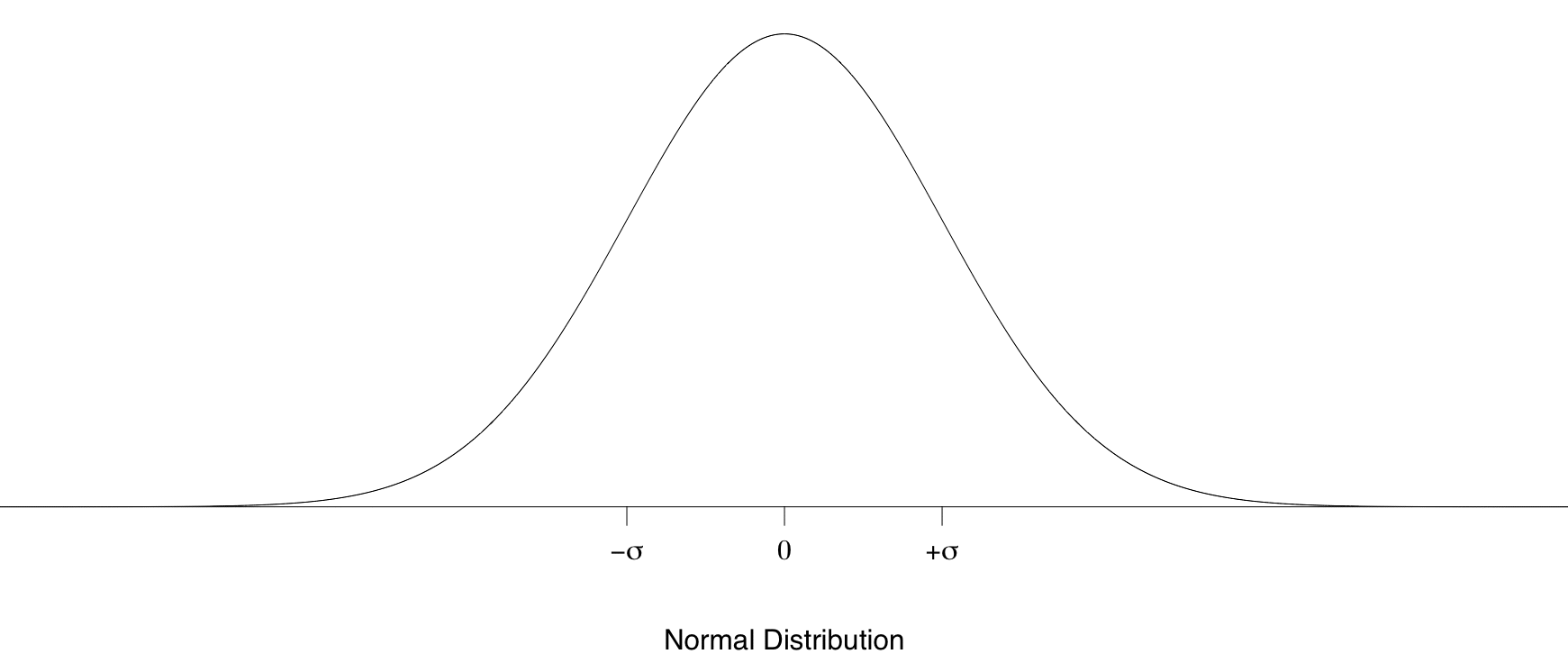
正态分布 (normal distribution) 又叫高斯分布 (Gaussian distribution),是重要的概率分布之一,其概率密度函数为
φμ,σ(x)=1√2πσe−(x−μ)22σ2
由于形似钟形,又经常称之为钟形曲线。在生产与科学实验中,很多随机变量的概率分布都可以近似用正态分布描述。例如生物体的身长、体重,地区降水量等等。除此之外,还有一些常见的概率分布是由它直接导出的,例如对数正态分布、t分布、F分布等等,导致经常遇到这种情况:
要使用xx检验,必须满足正态分布。
有人说过:直线属于人类,曲线属于上帝。每个人追求的曲线也许不同,男人追求不断向上的曲线,女人追求玲珑浮凸的曲线,而真正的上帝曲线应该是这个形似钟形的神秘曲线,无影无形,却又无处不在。
#幂律分布
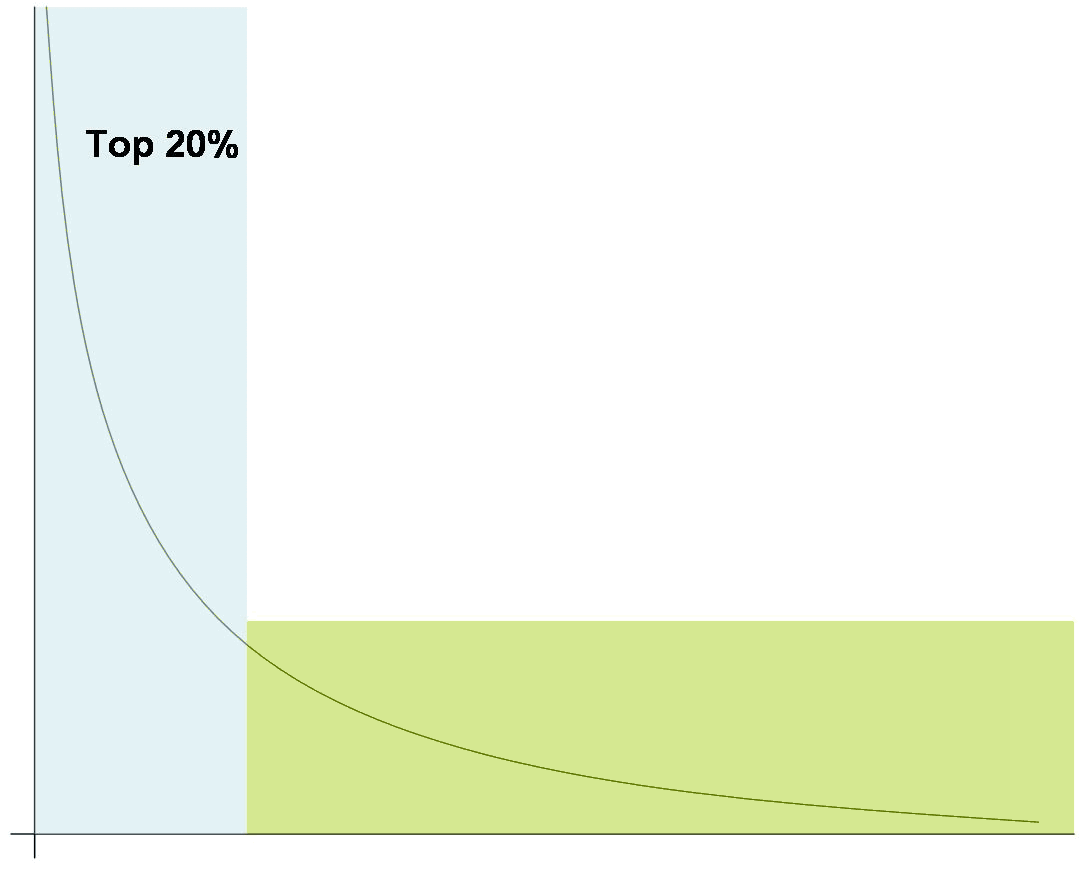
很早就知道二八法则的概念,最早是说社会上 20% 的人占有 80% 的社会财富,强调世界充满了重要的少数与琐碎的多数,这个法则在管理学、社会学等很多方面都有体现,再往上走一步,这种概率分布可以用一种更加科学的名词来表征,叫做幂律分布。
幂律分布 (power law distribution) 是一种常见的统计现象,简单地说就是两个变量为幂函数的关系,而这种简单的关系却能够与很多领域的实际情况相吻合,尤其是生物学、生态学这类典型的无标度网络。与随机网络不同,这种无标度网络的度常常是集散分布,大部分节点只有较少的连接,而少数节点有大量的连接。这类无标度网络的特性是:当节点意外失效或改变时,对网络的影响一般很小,只有 hub 节点受到改变,才会让网络产生剧烈的震荡。对于目前的中国,Mr. Xi 就是一个典型的 hub 节点。
复杂系统入门必修课——幂律分布
http://swarma.org/%E5%A4%8D%E6%9D%82%E7%B3%BB%E7%BB%9F%E5%85%A5%E9%97%A8%E5%BF%85%E4%BF%AE%E8%AF%BE-%E5%B9%82%E5%BE%8B%E5%88%86%E5%B8%83-%E5%85%A8%E7%BD%91%E7%8B%AC%E5%AE%B6/
统计学出身的我,持有这样一个观点:真实的数据不会说谎。
然而,我们接触到的收入数据却似乎存在着一些问题。
根据国家统计局的数据,2017年全国居民人均可支配收入是2.6万元,如果是正态分布的话,收入超过6万的人会很少。但实际上,早在2016年,就已经有20%居民的可支配收入超过了5.9万!(数据来源:国家统计局2017年统计年鉴)

最近几年,当统计数据显示北上广深的平均月薪近万或者过万时,都会引发大量北上广深年轻人“我又拖国家后腿”的吐槽。
而拥有可投资资产在1000万以上的“高净值人口”,在中国有10万人。
十万个千万富翁?富人比你想象的多很多!
富人为什么这么多?带着这个问题我请教了北师大系统科学学院的陈清华老师,终于了解到了真相。
原来,答案就在于幂律分布。

实际上,人们的收入服从幂律分布,而不是正态分布。这意味着用平均去代表整体的水平,是有严重偏差的。
一方面,人们的收入是不均匀的,根据幂律分布中的二八准则,20%的人掌握着80%的财富。
另一方面,这种不均匀极其严重。2016年,仅仅是最富有的8个人的财富,就超过了最贫穷的一半人口(36亿)的财富总和。(数据来源 新华社 http://www.xinhuanet.com/fortune/2017-01/17/c_1120324056.htm)
哈,富人不仅仅多,而且比你想象得更富!
在被现实一次次打脸后,我终于知道了原来幂律分布是这个样子,原来真实世界如此残酷!
更让我惊奇的是,陈老师还让我了解到,这些复杂系统中的问题竟然都和幂律分布有关:
二八准则、马太效应、黑天鹅、长尾理论、胖尾、无标度,它们之间究竟有什么区别和联系?
我一脸懵逼,学了四年的统计,幂律分布这么重要的普适规律,老师竟然没教过我?
真不明白为什么幂律分布仍然没有被列进统计学教科书 ?!
为了让更多像我一样的同学不再万脸懵懂,我果断出手,以集智学园课程大侦探的特殊身份——
划重点 !!!
▼
▼
邀请到北京师范大学陈清华老师、张江老师联手为大家来系统讲解这门复杂系统的入门必修课——
《复杂系统中的幂律分布》