生成随机数

原文出处：https://zhuanlan.zhihu.com/p/28133598 

真正的随机数是使用武力现象产生的，这里介绍的是由计算机按照一定数学方法生成的伪随机数，这里的“伪”是有规律的意思，因为用数学方法产生的随机数列是根据确定的算法推算出来的，严格说来并不是随机的。主要函数如下：

Y=rand %生成一个服从[0,1]上均匀分布的随机数
Y=rand(n)%生成n*n的随机数矩阵
Y=rand(m,n)%生成m*n的随机数矩阵

MATLAB统计工具箱中函数名以rnd结尾的函数用来生成常见分布的随机数。

R=binornd(N,p,m,n)%二项分布
R=chi2rnd(V,m,n)%卡方分布
R=evrnd(mu,sigma)%极值分布
R=exprnd(mu,m,n)%指数分布
R=frnd(V1,V2,m,n)%F分布
R=gamrnd(A,B,m,n)%Gamma分布
R=geornd(P,m,n)%几何分布
R=gprnd(K,sigma,theta,M,N....)%广义帕累托分布
R=hygernd(M,K,N)%超几何分布
r=logrnd(quantiles,m,n)%对数正态分布
R=normrnd(mu,sigma)%正态分布
R=poissrnd(lambda,m,n)%泊松分布
R=trnd(V,m,n)%t分布
R=unifrnd(A,B,m,n)%连续均匀分布

m,n均为矩阵维度，mu和sigma为均值和标准差。

举例：

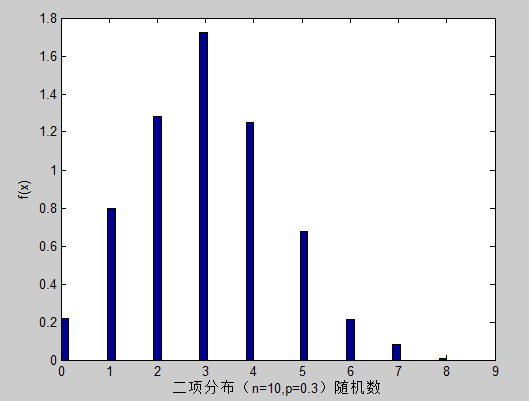
%调用random函数生成1000行1列的随机数向量x,元素服从二项分布B(10,0.3)
x=random('bino',10,0.3,1000,1);
[fp,xp]=ecdf(x);
ecdfhist(fp,xp,50);
xlabel('二项分布（n=10,p=0.3）随机数');
ylabel('f(x)');

生成多元分布随机数

MATLAB自带多元分布随机函数有mnrnd（多项分布）,mvnrnd,mvtrnd,wishrnd等。

三项分布：如果做一件事情有三种情况，第一种情况k1出现的概率为p1，第二种情况k2出现的概率为p2，第三种情况k3出现的概率为p3

则这种情况发生的总共的可能种数有：A=C（k1+k2+k3，k1）*C(k2+k3 , k2)*C(k3 , k3)

C（n ， k)表示从n个抽出k个的组合总数。

则概率为：P=A*p1^k1*p2^k2*p3^k3.

n=100; %多项分布的参数n
p=[0.2 0.3 0.5];%多项分布的参数p
%调用mnrnd函数生成10组3项分布随机数
r=mnrnd(n,p,10)
r =

    14    30    56
    16    31    53
    21    25    54
    22    26    52
    13    38    49
    17    27    56
    15    43    42
    19    35    46
    18    30    52
    21    33    46
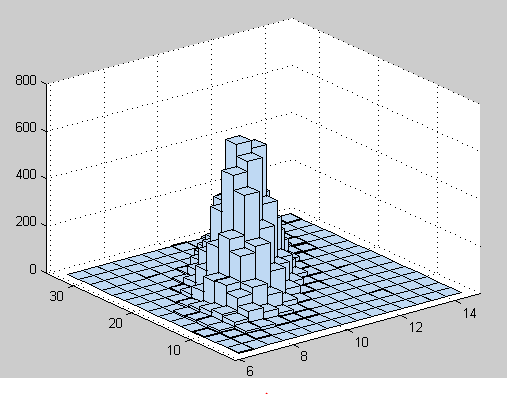
%调用mnrnd函数生成10000组3项分布随机数
r=mnrnd(n,p,10000);
hist3(r(:,1:2),[50,50])%绘制前两维的频数直方图

二元正态分布

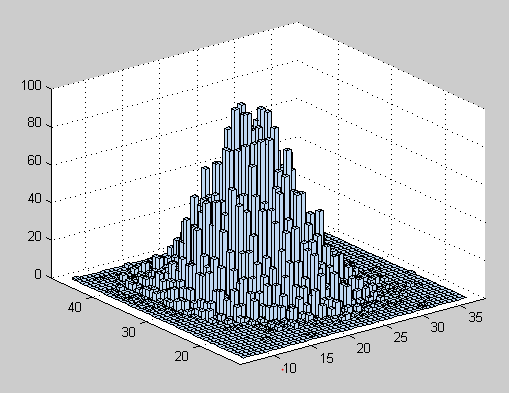
mu=[10 20];    %二元正态分布的均指向量
sigma=[1 3;3 16] %二元正态分布的协方差矩阵
%调用mvrnd函数生成10000组二元正太分布随机数
xy=mvnrnd(mu,sigma,10000);
hist3(xy,[15,15]); %绘制二元正太缝补随机数的频率直方图