三段论与演绎推理

在日常生活和科学研究中，我们经常需要对很多的事情做出科学合理的判断，如明天是否要下雨？火车能否继续提速？相等的角是否是对顶角？函数是否单调递增？宇宙飞船的速度达到多少才能飞出地球？等等。我们常说，只要前提条件满足，一切皆有可能。如阿基米德说，“给我一个支点，我将可以撬起地球。

这些判断是否正确就需要做出合情合理的逻辑推理，演绎推理就是其中一种应用普遍、结构简单、条理清楚、科学合理的逻辑推理，而演绎推理的基础就是三段论推理。

1.三段论推理的概念

那么什么是三段论推理呢？我们先来看一个故事：

三段论推理的理论最早是由两千多年前的古希腊先哲亚里士多德提出的。一天，亚里士多德和自己的学生在校园里散步，学生们提出请老师给他们讲讲什么是三段论，亚里士多德不紧不慢地说：“你的钱包在你身上，你的钱在你的钱包里，那么你的钱就一定在你身上，这就是三段论。”亚里士多德的话通俗易懂，学生们频频点头。

亚里士多德

亚里士多德（Aristotle，公元前384—前322），古希腊人，古代先哲，世界古代史上伟大的哲学家、科学家和教育家之一，堪称希腊哲学的集大成者。他是柏拉图的学生，亚历山大的老师。

公元前335年，他在雅典创办了一所叫吕克昂的学校，构建了自己的学派，这个学派的老师和学生们习惯在花园中边散步边讨论问题，因此被称为逍遥学派。亚里士多德一生勤奋治学，从事的学术研究涉及逻辑学、修辞学、物理学、生物学、教育学、心理学、政治学、经济学、美学、博物学等，写下了大量的著作，他的写作也涉及了伦理学、形而上学、心理学、经济学、神学、政治学、修辞学、自然科学、教育学、诗歌、风俗，以及雅典法律等。作为一位百科全书式的科学家，他几乎对每个学科都作出了重要贡献。马克思曾称亚里士多德是古希腊哲学家中最博学的人物，恩格斯称他是“古代的黑格尔”。亚里士多德的著作构建了西方哲学的第一个广泛系统，他的著作也是古代的百科全书。

亚里士多德的思想对人类的发展产生了极其深远的影响。他不但创立了形式逻辑学，还丰富和发展了哲学的各个分支学科，对科学的许多领域都作出了巨大的贡献，是最早论证地球是球形的人。

亚里士多德提出的三段论推理就是形式逻辑的基础，是演绎推理中的一种简单判断推理。

那么，什么是三段论推理呢？

简单地说，就是判断一个命题是否成立，需要做出三个步骤。

第一个步骤是给出一个一般性的原则，称为“大前提”；

第二个步骤是说明一个条件是附属于前面大前提的特殊化陈述，称为“小前提”；

第三个步骤是由此可以引申出一个特殊化的陈述，即为“结论”（符合一般性原则的结论）。

也就是说，三段论推理包含两个直言命题构成的前提（大前提、小前提），和一个直言命题构成的结论。

而且任何一个三段论都有而且仅有三个性质命题构成，其中两个是前提，一个是结论。

大前提：包含大项的前提。

小前提：包含小项的前提。

结论：包含小项和大项的命题。

每个项在其中两个不同的命题中各出现一次。

即一个正确的三段论有且仅有三个词项，其中联系大小前提的词项叫“中项”，在前提中出现两次；出现在大前提中，又在结论中做谓项的词项叫“大项”；出现在小前提中，又在结论中做主项的词项叫“小项”。如：

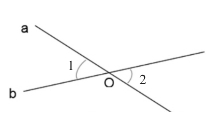
图1

所有的偶蹄目动物都是脊椎动物（大前提），

牛是偶蹄目动物（小前提）；

所以牛是脊椎动物（结论）。

又如：

所有的对顶角都相等（大前提），

如图1，∠1与∠2是对顶角（小前提）；

所以∠1与∠2相等（结论）。

上面的三段论推理中，“偶蹄目动物”是连接大小前提的中项，“脊椎动物”是出现在大前提中又在结论中做谓项的“大项”；“牛”是出现在小前提中又在结论中做主项的“小项”。

同样，“对顶角”是连接大小前提的中项，“相等”是出现在大前提中又在结论中做谓项的“大项”；“∠1与∠2”是出现在小前提中又在结论中做主项的“小项”。

三段论的特征就是通过中项在前提中的媒介作用把大项和小项连接起来，从而推出结论。

所以，三段论的实质是一种词项的外延关系的理论，是由两个性质命题推出一个新命题的过渡，之所以能过渡，是根据事物类的包含和排斥关系所进行的逻辑推导。也就是说，如果对一类事物的全部有所断定，那么对它的部分也就有所断定。如果对一类事物的全部有所否定，那么对它的部分也就有所否定。

三段论推理也是一种公理。公理的涵义就是要求公理具有明显的直观真理性，能够不证自明，公理内部前后要有严密的一致性、无矛盾性。

三段论的公理性在于：如果一类对象的全部都是什么，那么，它的小类，即部分对象也必然是什么；如果一类对象的全部都不是什么，那么，它的小类，即部分对象也必然不是什么。这就是说，如果对某类对象的全部都有所断定，那么，对它的部分对象也就有所断定。

三段论的大前提、小前提、结论这三个部分，从逻辑结构上说，是缺一不可的。但三段论的每一段式并非都是有效的，事实上，三段论式中的大部分可能是无效的，或者是可有可无的。因此，三段论在日常语言的表达中，就可以省略其中的某个部分。

在日常语言的表达中省略了大前提或者小前提或者结论的三段论，就称为三段论的省略式，也可以称为省略三段论。

值得注意的是，省略三段论所省略的，只是语言表达，而不是它的逻辑结构。也就是说，省略三段论所省略的部分，在逻辑结构上，仍是它的必要部分，只不过没有把它在语言上表达出来而已。

省略三段论有三种形式：

第一，省略大前提。省略的大前提往往是得到了普遍承认的一般性原理；

第二，省略小前提。省略的小前提往往是不言而喻的事实；

第三，省略结论。省略的结论，因为其显而易见，不说出来往往比说出来更有力。

下面举例加以说明：

（1）省略大前提

①你是数学学院的学生，你应当学好数学；

②在三角形ABC中，∠A+∠B=90°，则三角形ABC是直角三角形。

例①省略了大前提“凡是数学学院的学生都应该学好数学”。例②省略了大前提：“凡是三角形中有两个角之和为90°，则这个三角形是直角三角形”。

（2）省略小前提

①凡是在校学生都应该好好学习，张三同学也不例外；

②这个三角形不是等边三角形，因为等边三角形是三条边都相等的三角形。

例①省略了小前提“张三是在校学生”。

恢复其三段论完整式是：“凡是在校学生都应该好好学习，张三是在校学生，张三同学也不例外”。

例②省略的小前提是“这个三角形有两边不相等”。

恢复其完整式是“三条边都相等的三角形是等边三角形，这个三角形有两边不相等，这个三角形不是等边三角形”。

（3）省略结论

①业余办学形式是群众所欢迎的，函授教育就是一种业余办学形式。

②三个角都相等的三角形是等边三角形，三角形ABC就是这样的三角形。

例①省略的结论是“函授教育形式是群众所欢迎的”。

例②省略的结论是“三角形ABC是等边三角形”。

三段论省略式也有弱点，一些前提虚假或推理错误的三段论，经省略后，很可能使这些毛病掩盖起来，不易察觉。因此，在判定省略三段论的有效性时，有时就需要先把省略部分补充进去，把省略三段论恢复成完整形式。

省略三段论的恢复，有以下步骤：

首先，确定结论是否被省略。在结论前，通常以“因此”“所以”这样的联词，根据是否有这样的联词，容易断定结论是否被省略。

其次，如果结论没有被省略，那么，根据结论就可以确定大、小项。如果大项没有在省略式的前提中出现，则说明省略的是大前提。如果小项没有在前提中出现，则说省略的是小前提。

最后，把省略的部分补充进去，并进行适当的整理，就得到了省略三段论的完整形式。

在恢复省略三段论时，要注意两点：

第一，不违反省略三段论的原意。一般地说，省略三段论的被省略部分的内容，是显而易见的，正因为如此，它才可以省略。要按照省略三段论这种明显的原意进行恢复，不能为了避免省略三段论恢复后出现形式错误而违反它的原意进行恢复。

第二，如果对省略三段论原意的理解存在歧义，那么，在恢复时所补充的判断，应该力求是真实的。如果不违背原意去补充一个真实的判断作为前提或结论，却补充了一个虚假的判断，这就失去了恢复省略三段论的意义。

三段论必须是有效的，所谓推理的有效性，就是通过推理，从真的前提必然只能得到真的结论，如果一个推理形式能从真前提推出假结论，那么这个推理形式是无效的，三段论推理也是如此。

2.三段论的推理规则

人们根据三段论公理，总结出三段论的一般推理规则，使之成为判定三段论是否有效的标准。三段论的一般规则共有七条，前三条是关于词项的规则，后四条是关于前提与结论的规则。

（1）一个正确的三段论，有且只有三个不同的词项。

例如：①同位角相等，相等的角是同位角，所以同位角是同位角。

②运动是永恒的，足球运动是运动；所以足球运动是永恒的。

上述推论①仅有两个词项，造成了无意义的同语反复，不可能推出什么新的断定。②是错误的，其中的项“运动”在大小前提中表达的不是同一概念，大前提中的“运动”是哲学意义上概念，指物质的根本属性之一。小前提中的“运动”指“体育运动”，这种表面上是三个词项，实质是四个词项的错误，就叫做“四词项错误”。

（2）三段论的中项至少要周延一次。

如果中项不周延，我们看会是什么情况。

例如：大学教授是知识分子，博士生是知识分子，所以，博士生是大学教授。

由于作为中项的大学教授没有周延，所以得出的结论没有依据也不可靠。

又如：某系同学都是共青团员，某班同学都是共青团员，所以，某班同学都是某系的学生。

上面的中项两次不周延的推理显然无法得出结论，因为某班同学也可能是某系的学生，也可能不是。

所以，三段论的中项至少要周延一次。

例如：有一个三角形，它的三条边分别是3cm、4cm、5cm，判断这是什么三角形？

由勾股定理可知：

凡是三角形一边的平方等于其他两边的平方之和（中项），那么这个三角形都是直角三角形；

已知的三角形（三条边分别是3cm、4cm、5cm）的一边平方等于其他两边平方之和（中项）；

所以这个三角形是直角三角形。（符合规则2，所以结论是正确的）

如果中项周延一次，那么就会有一个中项的全部外延和大项或小项发生了肯定或否定的关系，从而产生媒介作用，使大小前提发生联系推出必然结论。

又如：①知识分子是劳动者，李教授是知识分子，所以李教授是劳动者。

②知识分子不是剥削者，李教授是知识分子，所以李教授不是剥削者。

上述例子都是仅有一个中项是周延的，它们都能推出必然结论，大小前提与结论的联系都是必然的。

如果中项周延两次，只要大小前提不都是否定的，那么，中项的全部外延就会分别与大项、小项发生联系，起到联结大小项的作用，从而使三段论推出必然的结论。

例如：

①分数是有理数，分数也是实数，所以有的实数是有理数；

②π不是有理数，π是实数，所以，有的实数不是有理数；

③π不是有理数，π不是代数数（指任何整系数多项式的复根），所以，不是有理数的数就不是代数数。

上述三个例子，前两个都是正确的，第三个是错误的。前两个的前提或都是肯定的，或一个肯定一个否定，这样，中项与大小项均发生了联系，中项就起到联结大小前提的作用，从而使这两个三段论推出必然结论。第三个例子，中项虽然周延两次，但两个前提都是否定的，中项无法起到联结大小前提的作用，因此不能推出结论。

（3）在前提中不周延的词项，在结论中也不得周延。

如果前提中的大项或小项是不周延的，那么它们的大项或小项的外延就没有被全部断定，若结论中的大项或小项变为周延的，那么就等于断定了大项或小项的全部外延。这样，造成了前后不一致，所推出的结论当然是不可靠的，其结论也不是由前提必然推出的。违反这条规则，所犯的逻辑错误称为“大项不当扩大”或“小项不当扩大”。

例如：

①先进工作者都是工作有成绩的人，老王不是先进工作者，所以老王不是工作有成绩的人。

②黄马是马，白马不是黄马，所以，白马不是马。

③某人是教授，某人是北京大学的，所以，北京大学的都是教授。

④高尔基没有上过大学，高尔基是作家，所以，作家都没有上过大学。

上面的例子①、②所犯的逻辑错误是“大项不当扩大”；例③、④所犯的逻辑错误是“小项不当扩大”。从上面的例子来看，违反本条规则所推出的结论是不可靠的。

（4）两个否定前提不能推出结论。

如果两个前提都是否定的，那么中项同大小项发生排斥。这样，中项就无法起到联结大小前提的作用，小项同大项的关系也就无法确定，因而推不出结论。

例如：①A≠B，A≠C，所以B≠C。

②羊不是肉食动物，而虎不是羊，所以虎不是肉食动物。

上面两例，前提都是真实的，但由于形式无效，所以推出的结论有或然性。

（5）前提有一个是否定的，其结论必是否定的；若结论是否定的，则前提必有一个是否定的。

例如：若三角形不是直角三角形，则这个三角形不可能有两个角互余。

又如：A≠B，A=C，则B≠C。

该规则是导出规则。若一个三段论的大前提是否定的，那么，中项与大项这两者的外延就必然是互相排斥的，所以小前提就只能是肯定的。这样，通过中项的媒介作用，小项就会与大项的外延相排斥，从而推出必然性结论。同理，若小前提是否定的，那么，中项与小项的外延相排斥，大前提只能是肯定的，则中项与大项的外延就必然具有相容关系。

又如：任何有神论都不是唯物论，所有宗教神学都是有神论，所以所有宗教神学都不是唯物论。（正确）

（6）两个特称前提推不出结论。

如：有些工人是先进工作者，有些教师是先进工作者，所以，有些工人是教师（没有必然性）。

又如：x=1是方程x2-1=0的解，x=-1也是方程x2-1=0的解，则-1=1，得出错误结论。

（7）前提中有一个是特称的，结论必须也是特称的。

如：所有的学生党员都是成绩优秀者，我们班有些同学是党员。所以，我们班有些同学是成绩优秀者。

又如：对所有的实数x，f（x）=x2+x+1>0恒成立，因为x=-5是实数，则f（-5）>0。

所以，不同形式、结构的三段论，必须符合相应的规则，才能得出必然的结论。

下面我们来看看什么是逻辑推理，重点讨论一下演绎推理。

逻辑推理是人们正确的做事和对事情做出正确判断所必需的思维基础。常见的逻辑推理就有类比推理，归纳推理和演绎推理。

类比推理亦称“类推”，根据两个对象在某些属性上相同或相似，通过比较而推断出它们在其他属性上也相同的推理过程。它是从观察个别现象开始的，因而近似归纳推理，但它又不是由特殊到一般的推理，而是由特殊到特殊的推理。

例如：在平面几何中，如果三角形ABC是直角三角形（如图2），∠C是直角，由勾股定理可知，其三边满足AC2+BC2=AB2；

那么，在空间几何中，给出一个直角三棱锥V-ABC（如图3），其中∠AVB=∠BVC=∠CVA=90°，你能得出什么结论？

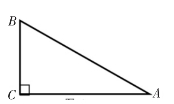
图2

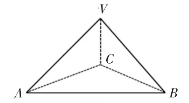
图3

类比勾股定理，线和面对应，我们就可得到：

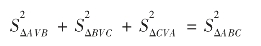
经过证明，结论是正确的。

归纳推理，就是根据一类事物的部分对象具有某种性质，推出这类事物的所有对象都具有这种性质的推理，叫做归纳推理（简称归纳）。归纳推理是从特殊到一般的推理。

如：在一个平面内，直角三角形内角和是180°；锐角三角形内角和是180°；钝角三角形内角和是180°；直角三角形，锐角三角形和钝角三角形是全部的三角形；所以，平面内的一切三角形内角和都是180°。这是完全归纳法，因为三角形按角分只有这三类，所以结论是正确的。

又如著名的哥德巴赫猜想，对于大于4的偶数，都可以表示为一个素数加一个素数，如：6=3+3，8=5+3，10=3+7=5+5，12=5+7，…，100=3+97=11+89=17+83=29+71=41+59=47+53，等等。

由此可以断定，对所有大于4的偶数，都可以表示为一个素数加一个素数。这是不完全归纳法，不可能把所有的偶数都加以验证，所以得到的结论只能算是猜想，正确与否还需进行严格的证明（哥德巴赫猜想直到现在还没有被完全证明，但也没有被否定）。

所谓演绎推理，就是从一般性的前提出发，通过推导即“演绎”，得出具体的陈述或个别结论的过程，前面我们说过，三段论就是演绎推理的基础。

关于演绎推理，还可以有以下几种说法：

①演绎推理是由一般到特殊的推理；

②演绎推理是前提蕴涵结论的推理；

③演绎推理是前提和结论之间具有必然联系的推理；

④演绎推理就是前提与结论之间具有充分条件或充分必要条件联系的必然性推理。

演绎推理的逻辑形式对于理性的重要意义在于，它对人的思维保持严密性；演绎推理的最典型、最重要的应用，通常存在于逻辑和数学证明中。

亚里士多德是古代知识的集大成者，他是主张进行有组织的研究演绎推理的第一人。

作为自然科学史上第一个思想体系的光辉的例子是欧几里得（Euclid）的几何学。欧几里得是古希腊的伟大数学家，他是以他的《几何原本》而著称于世的。欧几里得的巨大历史功勋不仅在于建立了一种几何学，而是在于他首创了一种系统的逻辑研究方法，这种方法带给后人的贡献，甚至超过了几何学本身。

欧几里得也是第一个将亚里士多德用三段论形式表述的演绎法用于构建实际知识体系的人，欧几里得的几何学正是一门严密的演绎体系，它从为数不多的公理出发推导出众多的定理，再用这些定理去解决实际问题。事实上，欧几里得本人对它的几何学的实际应用并不关心，他关心的是他的几何体系内在逻辑的严密性。欧几里得的几何学是人类知识史上的一座丰碑，它为人类对知识的整理、系统阐述提供了一种模式。从此以后，将人类的知识整理为从基本概念、公理或定律出发的严密的演绎体系成为人类的梦想。直到今天，他所创建的这种演绎系统和公理化方法，仍然是科学工作者离不开的东西。如后来的科学巨人麦克斯韦（James Clerk Maxwell，1831—1879）、牛顿（Isaac Newton，1642—1727）、爱因斯坦（Albert Einstein，1879—1955）等，在创建自己的科学体系时，无不是对这种方法的成功运用。

演绎推理可以分为三段论推理、假言推理、选言推理、关系推理等形式。

三段论推理前面已有详述，就不在此赘述。

3.演绎推理的其他几种形式

（1）假言推理

假言推理是以假言判断为前提的推理。假言推理分为充分条件假言推理和必要条件假言推理两种。

1）充分条件假言推理的基本原则是：小前提肯定大前提的前件，结论就肯定大前提的后件；小前提否定大前提的后件，结论就否定大前提的前件。如下面的两个例子：

①如果一个数的末位是0，那么这个数能被5整除；760这个数的末位是0，所以这个数能被5整除；

②如果一个图形是正方形，那么它的四边相等；这个图形四边不相等，所以，它不是正方形。

两个例子中的大前提都是一个假言判断，所以这种推理尽管与三段论有相似的地方，但它不是三段论。

2）必要条件假言推理的基本原则是：小前提肯定大前提的后件，结论就要肯定大前提的前件；小前提否定大前提的前件，结论就要否定大前提的后件。如下面的两个例子：

①只有肥料足，菜才长得好；这块地的菜长得好，所以，这块地肥料足。

②育种时，只有达到一定的温度，种子才能发芽；这次育种没有达到一定的温度，所以种子没有发芽。

（2）选言推理

是以选言判断为前提的推理。选言推理分为相容的选言推理和不相容的选言推理两种。

1）相容的选言推理的基本原则是：大前提是一个相容的选言判断，小前提否定了其中一个（或一部分）选言支，结论就要肯定剩下的一个选言支。

例如：这个三段论的错误，或者是前提不正确，或者是推理不符合规则；这个三段论的前提是正确的，所以，这个三段论的错误是推理不符合规则。

2）不相容的选言推理的基本原则是：大前提是个不相容的选言判断，小前提肯定其中的一个选言支，结论则否定其他选言支；小前提否定除其中一个以外的选言支，结论则肯定剩下的那个选言支。例如下面的两个例子：

①一个词，要么是褒义的、要么是贬义的，要么是中性的。“结果”是个中性词，所以，“结果”不是褒义词，也不是贬义词。

②一个三角形，要么是锐角三角形，要么是钝角三角形，要么是直角三角形。这个三角形不是锐角三角形和直角三角形，所以，它是个钝角三角形。

（3）关系推理

关系推理是前提中至少有一个是关系命题的推理。

下面简单举例说明几种常用的关系推理：

1）对称性关系推理，如1米=100厘米，所以100厘米=1米；

2）反对称性关系推理，a大于b，所以b小于a；

3）传递性关系推理，a>b，b>c，所以a>c。

演绎推理是严格的逻辑推理，演绎推理的基本要求是：一是大、小前提的判断必须是真实的；二是推理过程必须符合正确的逻辑形式和规则。演绎推理的正确与否首先取决于大前提的正确与否，如果大前提错了，结论自然不会正确。

同样，逻辑推理能力也是一种根据给出的条件，找出其内在的逻辑关系从而推理出符合逻辑关系的结论的能力。只有具备了逻辑推理能力，才能对事物做出符合逻辑关系的正确判断，因此逻辑推理能力也是每个人的重要的基本素质之一。