历法与日历中的数学
2017年6月7日,是一个非常重要的日子,全国940万高三毕业生走向高考考场,参加一年一度的全国高考。高考促进人的发展,高考改变人的命运,2017年也是“文革”后恢复全国高考40周年纪念日。
从中我们可以看出,公元纪年、日期、时间已经深深扎根于我们的日常生活,我们研究人类文明,研究人类历史,设计人类未来都离不开纪年、日期与时间,没有纪年、日期、时间是不可想象的,这就是我们通常所说的历法。
比如历法中的日历(也包括月历、年历)就已经是我们日常生活、生产中必不可少的工具。我们聪明的祖先,在几千年前就根据日月星辰的变化规律,制定了这个记载时间流逝的工具。今天,就让我们一起来探索历法与日历中的一些简单规律吧!
我们先来看一道与古历法有关的趣题。
题目是:“当年苏武去北边,不知去了几多年。分明记得天边月,二百三十五番圆。”这是我国明代数学家程大位在其《算法统宗》中的一道题目。
苏武是西汉的使者,在公元100年奉命出使匈奴,被匈奴扣留并多方威胁诱降,苏武始终坚贞不屈,大义凛然。后被流放北海(今贝加尔湖)牧羊,生活非常艰苦,不知过了多少年月才被释放,只记得天上月亮整整圆了235次,问苏武被流放了多少年?
我们知道,月亮每个月圆一次,一年有12个月,月亮一年圆12次,所以要求苏武流放了多少年,就是要求235里面有几个12。
由于235÷12=19(年)……7(月)
需要注意的是,不能认为商是19,余数是7,就是19年另7个月。
古人通过长期观测得出的数据是,“一岁三百六十五日四分日之一”,即一年为365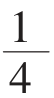 天,同时得出一月为
天,同时得出一月为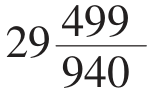 天(这也是我国古算经《周脾算经》中记载的古历法)。
天(这也是我国古算经《周脾算经》中记载的古历法)。
这样一年应该有

这说明19年中应有7个闰月(中国农历)。
所以,苏武在北海流放了235个月,正好就是19年。
那我们今天所使用的历法又是如何形成的,又是如何规定的呢?
我们知道,一年有12个月,共计365天,一天有24小时,年有闰年,月有闰月,月有大小,这些都是如何规定的,有什么依据和规律,人们是如何计算这些时间的,这就是天文历法所要研究的内容。
世界上的历法共有三类:
分为阳历、阴历和阴阳合历,三种。
阳历亦即太阳历,其历年为一个回归年,就是以地球绕太阳运转一圈的时间为一年,年的月数和月的日数可以人为规定,现时国际通用的公历(格里高利历)和中国的干支历即属于太阳历这一类。
阴历亦称月亮历,或称太阴历,其历月是一个朔望月,就是以月球绕地球运转一圈的时间为一个月,只有年的月数可以人为地规定,历年为12个朔望月,其大月30天,小月29天,伊斯兰历即为阴历的一种。
阴阳历是既兼顾了阳历的回归年又兼顾了阴历的朔望月,有非常明显的平年和闰年之分,年天数差异较大。历月为朔望月,因为12个朔望月与回归年存在一定的差别(少11天左右),所以阴阳历中设置了闰月,用以协调回归年和朔望月之间的关系,存在闰月的年份中一年为十三个月(朔望月),也是闰年。因此这种历法既与月球绕地球运转周期相符,又与地球绕太阳周期运动相符合。如中国的汉历(农历)、藏历等。所以,中国的汉历并不是阴历,而是阴阳合历,也叫农历。
农历中的阴历成分和阳历成分各有用处。
阴历可以指明月亮的盈亏,还可以预告潮汐的大小。
阳历的用处更大,二十四节气就是中国古代的一大发明,它表明了地球在轨道上的位置,反映了太阳的周年运动,最适合指导农事活动,因此作为阴阳合历的中国传统历法就叫做农历。
中国始有历法大约在四千多年以前。根据甲骨文中的一页甲骨历,证明殷代的历法已具有相当的水平,这一页甲骨历是全人类最古老的历书实物,这页甲骨历也就叫日历。
中国最早的纪年是干支历。其形成有一个过程,它由纪日开始。干支纪日早在中国商代的时候就已经出现,春秋战国时期已采用十二地支纪月。西汉末至今,一直用干支来纪年。唐以后,五代历书月名开始注以干支,北宋时又将十天干支、十二地支配合以纪时,至此年、月、日、时分别全以干支注记,干支历日趋完整。
干支历以立春为岁首,年长即回归年,用二十四节气划分出十二个月(即寅月、卯月、辰月等),每个月含有两个节气,没有闰月。干支历与地球环绕太阳的周期运动有关,它能反映出一年四季的气候变化。自古以来,干支历一直为中国官方和民间所普遍认识,应用于天文、风水、命理、选择术和中医等学科上,并为历朝官方历书(即黄历)所记载。如《红楼梦》第九十五回:“是年甲寅年十二月十八日立春,元春薨日是十二月十九日,己交卯年寅月”。又如1894年(甲午年)的“甲午战争”,1898年的“戊戌变法”等,这里更是明确地指出干支历在纪年纪月时的特点。
而农历和干支历是两种不同的历法,两者在年份起点、月份划分规则、每年天数等皆不同。
太阳、月亮是人们挂在天上的日历。年复一年,地球围绕着太阳不停运转,地球上的万物也在日月轮回中生息繁衍。
那我们来看中国的农历是如何具体规定的。
我们知道,地球绕太阳转一圈的时间是365天5小时48分46秒,约3 65.2422天;月亮绕地球一周的时间为27天7小时43分11.51秒。每个月的时间应该是365.242的十二分之一,即30天10小时29秒,而按月历是月亮绕地球一圈为一个月,因此这其中就有误差。那么如何弥补这些误差呢?
农历是按照月亮的圆缺即朔望月安排大月和小月。一个朔望月的平均长度是29.5306日,是月相盈亏的周期。农历规定,大月30天,小月29天,这样一年12个月共354天,这样十二个朔望月构成汉历年,长度为29.5306×12=354.3672日,比回归年(地球绕太阳一周的时间)365.2422日少10.88天(将近11天),每个月少0.91天(近1天)。
如果按上述规定制定历法,就会出现天时与历法不合、时序错乱颠倒的现象。
为了克服这一缺点,我们的祖先在天文观测的基础上,找出了“闰月”的办法,保证我国农历年的正月到三月为春季,四月到六月为夏季,七月到九月为秋季,十月到腊月为冬季,也同时保证了农历岁首在冬末春初。
闰月计算法:农历年中月以朔望月长度29.5306日为基础,所以大月为30日,小月为29日。为保证每月的头一天(初一)必须是朔日,就使得大小月的安排不固定,而需要通过严格的观测和计算来确定。因此,农历中连续两个月是大月或是小月的事是常有的,甚至还出现过如1990年三、四月是小月,九、十、十一、十二连续四个月是大月的罕见特例。如春节的前一天常称为大年三十,但有不少年的农历十二月只有29天。
那么多长时间加一个闰月呢?最好的办法就是求出回归年日数与朔望月的日数的最小公倍数。
我们希望m个回归年的天数与n个朔望月的天数相等,也就是应有等式:
m×365.2422=n×29.5306
在这个等式中我们不能直接求出m和n,但可以求出它们的比例。
其近似值为: =
=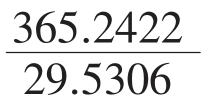 =12.368262≈
=12.368262≈
由此可知,19个回归年中必须加7个闰月。
19个回归年中加7个闰月的结果比较:
19个回归年=19×365.2422=6939.6018(天)
一个朔望月有29.5306天,19年加7个闰月共有235个朔望月,则
235个朔望月=235×29.5306=6939.6910(天)
19个回归年中加7个闰月后,矛盾消除得只差:
6939.6910-6939.6018=0.0892(天)
即2小时9分多,这已经是够精确的了。
所以,农历就采用了19年加7个闰月的办法,即“十九年七闰法”,把回归年与农历年很好地协调起来,使农历的元旦(春节)总保持在冬末春初。古人把235个朔望月称之为“闰周”。
农历置闰的方法可以使农历年的平均长度接近回归年,而农历中的月又有鲜明的月相特征,保持了阳历和阴历两全其美的特点。
农历闰哪个月,决定于一年中的二十四个节气。
我国农历将二十四个节气分为十二个节气和十二个中气。
现在的置闰方法是两个冬至之间,如仅有12个月则不置闰,若有13个月即置闰。置闰的月从“冬至”开始,当出现第一个没有“中气”的月份,这个月就是闰月,其名称是在前个月的前面加一个“闰”字。
一般每过两年多就有一个没有中气的月,这正好和需要加闰月的年头相符。所以农历就规定把没有中气的那个月作为闰月。
例如2001年5月21日,农历四月二十九日,是中气小满,再隔一个月后,6月21日农历五月初一才是下一个中气夏至,而当中这一个月(2001年5月22日—2001年6月20日)没有中气,就定为闰月。因为它跟在四月后面,所以叫“闰四月”。
农历闰月年份的天数一般长达384天,这样的年份在所有农历闰月的年份当中是最常见的,出现率很高,例如在2001年至2100年这100年当中,一共有37个农历闰月的年份,其中长达384天的就有34个,例如,2001年、2004年、2009年、2012年、2014年、2017年、2020年、2023年等,出现率高达92%。
有少数农历闰月年份的天数比较短,这样的农历闰月年份的天数也长达383天。从1534年至2134年这600年里,一共只有17次,分别是1550年、1558年、1585年、1648年、1710年、1743年、1805年、1808年、1841年、1868年、1903年、1930年、1957年、1965年、1993年、2055年、2088年。
最长的农历闰月年份的天数可长达385天,这样的农历闰月年份是很罕见的。从公元前221年至公元2100年的2321年里,一共只有12次。其中,从1501年至2100年这600年里出现了7次,分别是1580年、1599年、1661年、1925年、1944年、1987年和2006年。
如果一年闰正月,原则上春节、元宵节是过第一个正月的,到了闰正月的时候则不过节。
如果一年闰腊月,那么,除夕过第二个腊月的最后一天,因为第二个腊月的最后一天才是整个农历年的最后一天。
月序的确定,是以冬至所在月为子,依照地支顺序,下一个月为丑,再下一个月为寅,如此类推,到下一个冬至所在月又回到了子。由于汉以后的历法都是建寅,以寅月为正月,这样冬至所在月必然是十一月。
中国的农历中有很多大家熟悉的传统节日,像春节(大年初一)、元宵节(正月十五)、端午节(五月初五)、中秋节(八月十五)、重阳节(九月初九)、腊八节(十二月初八)等都是农历的节日。每个月的初一是新月出现的那一天,月圆的那一天则在十五左右。而立春等节气是依据阳历的。
为此,唐代诗人李贺还专门写了一首闰月的诗:
闰月
[唐]李贺
帝重光,年重时。
七十二候回环推,
天官玉管灰剩飞。
今岁何长来岁迟,
王母移桃献天子,
羲氏和氏迂龙辔。
——《全唐诗·卷二八至六三》
下面我们来看公历的发展与制定规则。
我们知道,公历一年的时间是365天5小时48分46秒,约为365.242天,若平均分成12个月,则每个月的时间是365.242的十二分之一,即30天10小时29秒。但实际操作上是取整,平年为365天,“闰年”为366天。这种历法是一种太阳历,也是国际上通用的历法。
公历,可追溯到公元前46年古罗马凯撒大帝的历法改革,将一年定为365天,闰年366天,一年分为12个月,每四年加一天为闰日,这样算起来平均一年是365.25日。凯撒的名字叫儒略·凯撒(Julian Ceasar),所以由凯撒确立的这种历法又叫“儒略历”(Julian Calendar)。
从儒略历开始,为了弥补因人为历法规定造成的年度天数与地球实际公转周期的时间差,就设置了闰年,其中补上时间差的年份为闰年。
先看月份的设置,月份分大月小月,其中大月每月31天,有1,3,5,7,8,10,12月;小月每月30天,有4,6,9,11月;只有2月是28天(闰年的2月份为29天)。
年有平年闰年,其中平年一年365天,闰年一年366天(2月份增加1天,是29天)。
通常我们所说的一年有多少天多少小时多少分,但取整数365天还有多余的,累积达到24小时后,就多加一天的年是闰年。公历的平年只有365日,比回归年短约0.2422日,所余下的时间约为每四年累计一天,故第四年于2月末加1天(即2月29日),使当年的历年长度为366日,这一年就为闰年,也就是4年一闰。
为什么规定公历的2月是28天?这是古罗马在制定日历时,起初设想月份的单数为31天,双数为30天。但这样一年是366天,比365天多出一天,必须从12个月中抠出一天。因为在古罗马,执行死刑都在2月份,所以都认为这个月不吉利,那就从2月中抠出一天,成了29天。当时一罗马大帝出生在有30天的8月,比上一任出生在有31天的7月的大帝少一天。他就又从2月份中抠出一天,加到8月份。从此公历的2月就成了28天,本应是30天的8月份成了31天。
在凯撒建立新的历法时,还没有耶稣基督,所以那时候的年号与现如今是不同的,采用罗马建城纪年。现如今日历上公元元年的确立是在公元525年由东罗马皇帝迪奥(Dionysius Exiguus)开始,迪奥为了能够方便计算耶稣的复活日,于是将耶稣诞生的那一年定为公元元年。
现今国际通用的历法,即公历是“格里高利历”,由罗马天主教皇格里高利十三世(Pope Gregory 13)于公元1582年10月15日启用。格里高利历是在儒略历的基础上,对闰年设置作了一些调整,按儒略历,每四百年中有一百个闰日,格里高利历将一百个闰日减为九十七个。格里高利十三世作这个调整是出于宗教原因,是为了精确计算耶稣复活日。但实际上一个回归年为365.24219日,儒略历到公元1582年已经累计了十天误差(多了十天,或者说与实际季节相比慢了十天)。所以格里高利十三世下令公元1582年10月4日(儒略历)的下一天为公元1582年10月15日(格里高利历),星期保持连续不变。经过这样的调整之后,便完成了从儒略历到格里高利历的更替。但是这样产生了一个效应,便是从历史上看来公元1582年10月5日至14日这十天“凭空消失”了。其实是因为两种历法版本的更替,这十天从来也没有存在过,所以又称作“消失的十天”。目的是为了消除掉积累的误差。格里高利还重新修改了置闰法则,修改之后的格里高利历的平均历年长度已经达到了365.2422日。这就已经非常接近于真实的回归年长度了,可以说已经相当精确了。
格里高利重新修改后的置闰的法则是:
每400年有97个闰年。按照每四年一个闰年计算,平均每年就要多算出0.0078天,这样经过四百年就会多算出大约3天来。因此每四百年中要减少三个闰年。由于当时没有了解到每年要多算出0.0078天的问题,从公元前46年,到16世纪,一共累计多出了10天。这就是教皇格列高利十三世当时为什么将1582年10月5日人为规定为10月15日,并开始了新闰年规定。规定公历年份是整百数的,必须是400的倍数才是闰年,不是400的倍数的就是平年,即使是4的倍数也不是闰年。
这就是通常所说的,四年一闰,百年不闰,四百年再闰。比如,1700年、1800年和1900年为平年,2000年为闰年。
我们来看1950—2050年间的闰年:
1952,1956,1960,1964,1968,1972,1976,1980,1984,1988,1992,1996,2000,2004,2008,2012,2016,2020,2024,2028,2032,2036,2040,2044,2048。
今天,格里高利历已被世界广泛采用,也就是通常说的公历,已成为国际通用历法。
中国使用格里高利历是在公元1912年1月1日。但由于历史原因,依旧使用中华民国纪年。类似的情况如日本至今还保持着天皇年号纪年,比如平成某某年。
公元1949年10月1日,中华人民共和国成立,正式采用公元纪年法。
由于地球的自转速度逐渐降低,而公转速度则相对更加稳定,所以上述的系统经过更长的周期也会发生微小的误差。据计算,每8000年会有一天的误差,所以英国的天文学家John Herschel提议公元4000为平年,以后类推12000年,20000年亦为平年。但此提议从未被正式采纳。原因是到了4000年,地球自转的精确速度并非如今可以预测,所以届时参照真实数据方可作出判断。因此,在长远的将来,针对闰年的微小调整应该不是由预定的系统决定,而是随时间的变化而确定的。
下面我们来看一个小例子。
小芳今年10周岁,可她说她的生日一共才过了2次,你说可能吗?
答案是肯定的,因为她的生日2月29日是闰日,由于正常情况下四年一闰,也就是说,小芳每4年才能过一次生日。
我们现在常用的公历纪年表示方法多是用月历呈现的,也称日历。
日历是一种日常使用的物品,用于记载日期等相关信息。每页显示一日信息的叫日历,每页显示一个月信息的叫月历,每页显示全年信息的叫年历。
日历里面也隐藏着很多的数学规律。
让我们来看一张普通的日历,初步探索、了解一些特殊的规律。
(1)由于一个星期是7天,所以每个月的日历均分布在5行7列中,每行是连续自然数;每列成等差数列,公差是7;

(2)主对角线(左高右低)规律:如,7,15,23,31,是公差为8的一列数,次对角线是公差为6的一列数;
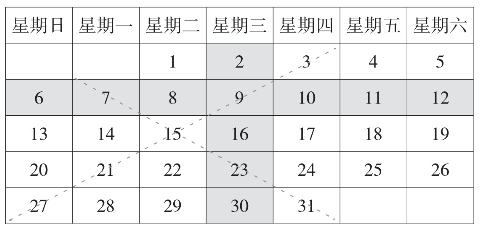
(3)如果设日历中的某一个数是A,那么日历中的所有数都可以用A的代数式来表示,如图:
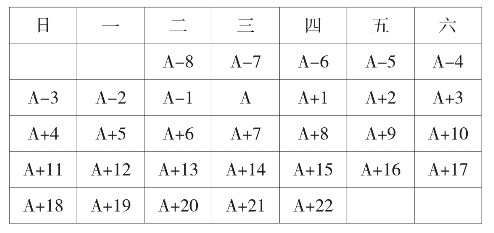
(4)用正方形在日历中任意框出4×4个数中,四个角上的4个数、中心2×2的4个数、两条对角线上的4个数以及来自不同行不同列的4个数之和都相等,而且是这16个数总和的四分之一;
对于正方形框出的2×2个数中,其对角线的数字之和相等,其4个数之和与不同行不同列的4个数的和也相等;
对于正方形框出的3×3个数中,也就是日历中的任意九宫格,只要知道中间一个数a,就可知道九宫格的其余8个数。而且经过中心a的行、列、对角线上的数字和均相等,并且是中心数的3倍。这九个数的和是中心数的九倍,即9a。
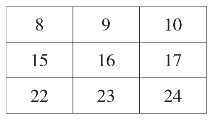
例题:用正方形在日历中框出4×4个数,在这4×4个数中,圈出不同行不同列的4个数字。
(1)若这4个数的和是72,请你写出这个方形;
(2)若这4个数的和是68,已知其中一个数是6,另一个数是21,则其他两个数分别是?
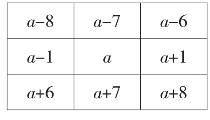
解(1):先写出中心2×2的4个数,设其中一个数是a,则这4个数的分布是

由于这4个数的和也是72,所以
a+a+1+a+7+a+8=4a+16=72
故,a=14
所以,框出的4×4正方形是:

(2)若这4个数的和是68,则所框出的4×4正方形是:
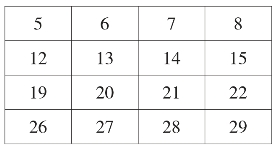
所以,已知其中一个数是6,另一个数是21,则其他两个数分别是12,29;或15,26。
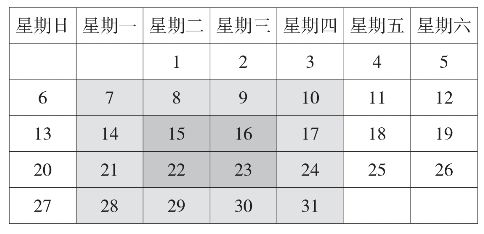
最后,我们来看国际魔术大师刘谦利用月历曾经表演过的一个魔术,叫“猜心术”。
随便取出一张月历如图,请一位观众在月历中任意画出一个4×4的正方形框,框内有16个数字。然后刘谦在一张纸上秘密写下一个数字,装入一个信封内。接下来,刘谦让这位观众在方框内任取一个数字,把这个数字所在的行和列上的其他数字都画掉,只留下这个数字;继续在方框内留下的数字中任选一个数字,把这个数字所在的行和列上的其他数字都画掉,只留下这个数字。以此类推,继续这样做下去,方框内就只剩下4个数字,刘谦请观众计算一下这4个数字之和,然后刘谦拿出信封内写在纸上的数字,就是这4个数字之和。观众茫然称奇。由于观众选取数字是随意的,这个和刘谦事先是怎么知道的呢?
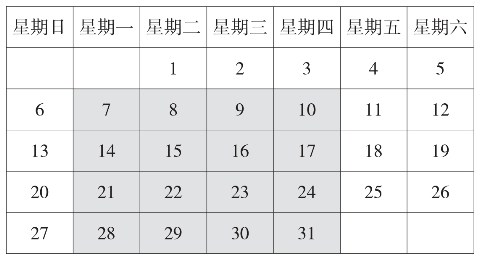
实际上,当观众选好4×4的正方形框后,刘谦只需记住左上角的第一个数字就可以了,比如图中的7,然后用4×7+48=76,在纸上写下76就可以了。此时观众选出的4个数字由于是来自正方形框内不同的行和列,可以证明,不管你如何选,这4个数字的和都是76。这也体现了日历表中蕴含的数字奥秘。
下面,我们给出一般关系的推证。
对于任意选取的4×4的正方形框,我们设左上角的第一个数字为N,如下表:
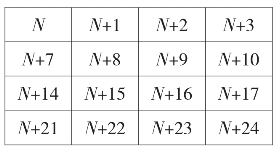
每一横行成等差数列,公差为1;每一纵列也成等差数列,公差为7。
而来自不同行、不同列的四个数字之和,相当于第一列的数字之和再加上1,2,3,即
(N+N+7+N+14+N+21)+1+2+3=4N+48
因此,只要知道左上角的第一个数字N,就可知道来自不同行、不同列的四个数字之和是4N+48。
当然,也可记住表中的其他数字,同样可以得出所求的和。如果设右上角的第一个数字是n,则所求数字之和是4n+36,等等。
而且来自不同行、不同列的四个数字之和与四个角上的四个数字之和、中心的四个数字之和也都相等。
人们的日常生活离不开日历,日历也不只是简单的记时记事,日历中的数学关系与规律对我们记住历史、研究历史、预测未来、训练思维都是必不可少的,其中的无穷奥秘还需要智者的不断探索,让日历为人类的文明发展发挥其更多更大的作用。
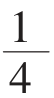 天,同时得出一月为
天,同时得出一月为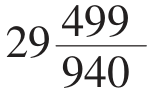 天(这也是我国古算经《周脾算经》中记载的古历法)。
天(这也是我国古算经《周脾算经》中记载的古历法)。
 =
=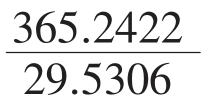 =12.368262≈
=12.368262≈










