河图洛书与幻方
数学中的智力游戏,思维含量高,趣味性强,是人们在智力活动中特别青睐的内容之一。如我们经常见到的九宫格游戏,就是其中一个著名的例子。也就是如何把1,2,3,4,5,6,7,8,9九个数字填入九宫格中,组成一个三行三列的矩阵(如图1所示),使其横行、纵列、对角线的和都相等。
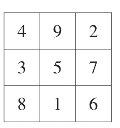
图1
其实这样一个简单的游戏,它的源头却是来自于古老的传说“河图”与“洛书”。“河图”与“洛书”也是华夏文化的源头之一。
相传,上古伏羲氏时代,在洛阳东北孟津县境内的黄河中浮出龙马,背负“河图”,献给伏羲。伏羲依此而演成八卦。后来周文王又依据伏羲八卦研究成文王八卦和六十四卦,并分别写了卦辞,后为儒家经典《周易》之来源。
又相传,古代大禹治水时,洛阳西洛宁县洛河中浮出神龟,其甲壳上有一图像,结构是载九履一,左三右七,二四为肩,六八为足,以五居中,五方白圈皆阳数,四隅黑点为阴数,时称“洛书”,献给大禹,古代也称此为龟书。大禹得到“洛书”以后,启示了他的灵感,所以把中国的水患平定了下来。大禹依此治水成功,遂划天下为九州。在中国文化的发展中,大禹功不可没,因他治水以后,中国九州才开始以农业立国,一直传承了几千年,大禹还依此定九章大法,来治理社会。
《易·系辞上》说:“河出图,洛出书,圣人则之”,指的就是这两件事,“图书”一词也源于此。
河图与洛书是中国古代流传下来的两幅神秘图案,历来被认为是河洛文化的源头。河图、洛书的数学价值也很高,根据河图画出的八卦实际上就是最早的二进制。18世纪德国数学家莱布尼茨创立二进制时,就是受八卦的启发,他还坦言创立二进制不过是重新发现了中国古代数学的秘密而已。洛书是现代组合数学中最古老的例子,是训练思维的数学幻方,如今在程序设计、图论等方面都有广泛的应用。
2014年11月11日,河图洛书传说,经国务院批准列入第四批国家级非物质文化遗产名录。
河图、洛书最早记录在《尚书》之中,其次在《易传》之中,诸子百家也多有记述。宋代理学大家朱熹在其易学著作《周易本义》中,第一次把“河图”“洛书”单列出来,并将其图置于卷首,以九为河图,十为洛书。河图洛书才正式流传于世。
看似简单而古老的河图洛书,却包含着神秘的数理关系。
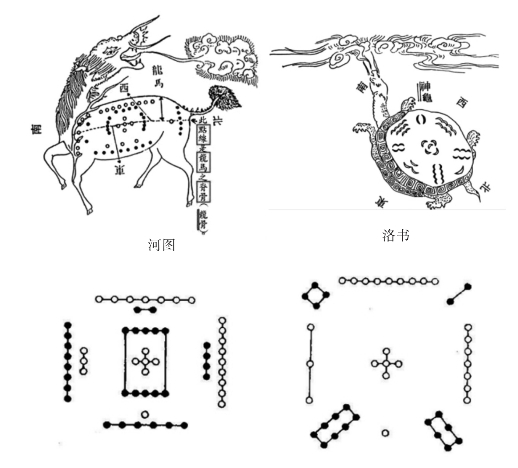
河图与洛书
1.河图包含的数理关系
(1)等和关系。除中间一组数(5,10)之外,纵向或横向的四个数字,其偶数之和等于奇数之和。
纵向数字:7,2;1,6;7+1=2+6
横向数字:8,3;4,9;8+4=3+9
并进一步得出推论:河图中,除中间一组数(5,10)之外,其余数字中奇数之和等于偶数之和,其和为20。
(2)等差关系。四侧或居中的两数之差相等。上(7—2);下(6—1);左(8—3);右(9—4);中(10—5),其差均为5。
(3)天地之数:河图共有10个数,1,2,3,4,5,6,7,8,9,10。其中1,3,5,7,9为阳,2、4、6、8、10为阴。阳数相加为25,阴数相加得30,阴阳相加共为55数。所以古人说:“天地之数五十有五”,即万物之数皆由天地之数化生而已。
2.洛书包含的数理关系
(1)等和关系。非常明显地表现为各个纵向、横向和对角线上的三数之和相等,其和为15。
(2)等差关系。细加辨别,洛书隐含着等差数理逻辑关系。
①洛书四边的三个数中,均有相邻两数之差为5,且各个数字均不重复。
上边[4,9,2],有9-4=5;
下边[8,1,6],有6-1=5;
左边[4,3,8],有8-3=5;
右边[2,7,6],有7-2=5。
显然这个特点与河图一样,反映出洛书与河图有着一定的内在联系。
②通过中数5的纵向、横向或对角线上的三个数,数5与其他两数之差的绝对值相等。
纵向│5-9│=│5-1│或9-5=5-1;
横向│5-3│=│5-7│或5-3=7-5;
右对角线│5-2│=│5-8│或5-2=8-5;
左对角线│5-4│=│5-6│或5-4=6-5。
综合以上分析,我们可以清楚地发现,其数理关系中对称性是河图、洛书图的基本特点,河图洛书还包含着基本的“和或差”的算术逻辑关系,尽管两者有所差别,但是它们表示的数理关系却有很多相似和共同之处。
世界万事万物都有其内在的规律和尚不知晓的奥秘,河图洛书的神秘传说,其实还蕴含着很多数理关系,这些关系也是现代数学的一些萌芽。如洛书实际上就是下面一个九宫格表(如图2),其每一行、每一列及两条对角线上的数字之和都相等(等于15)。这也就是现代所说的幻方。
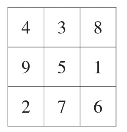
图2
幻方(Magic Square)是一种将1到n的若干个自然数数字安排在正方形格子中,使每行、每列和对角线上的数字和都相等的方法。
一般地,n阶幻方是指用前n2(n的2次方)个自然数组成的一个n阶方阵,其各行、各列及两条对角线所含的n个数的和均相等,这个和称为幻和。
如上面的洛书,就可以看作是一个三阶幻方,由1,2,3,4,5,6,7,8,9九个数字排成,幻和为15,中心数为5。
3.三阶幻方的构造
三阶幻方,又叫九宫格,这是幻方中最简单的一个幻方,因为2阶幻方是不存在的。
三阶幻方的构造方式有很多种,下面介绍几种供参考。
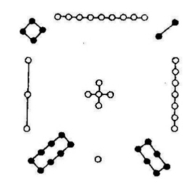
方法一:由于三阶幻方的幻和是15,而每行又有三个数,故中心数必须是5,含5的行、列、两对角线只能从下列四个算式中选取:1+9=10,2+8=10,3+7=10,4+6=10。这每对数的和再加上中心格的5都等于15,这四组数应分别填在横、竖和对角线的位置上。先填四个角,若填两对奇数,那么因三个奇数的和才可能得奇数,四边上的格里已不可再填奇数。若四个角分别填一对偶数,一对奇数,也行不通。因此,判定四个角上必须填两对偶数。对角线上的数填好后,其余格里再填奇数就很容易了。
方法二:古代南宋数学家杨辉概括的构造方法为:
九子斜排(把1,2,3;4,5,6;7,8,9斜排成三行,如图3),
上下对易(交换1和9的位置,如图4),
左右相更(交换7和3的位置,如图4),
四维挺进(把3,1,7,9插入所在行列中,完成幻方,如图5)。
其具体方法如图所示:
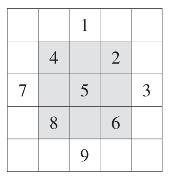
图3
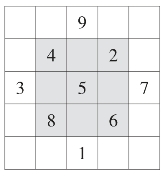
图4
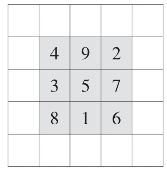
图5
方法三:中国古代九宫格的填法口诀是:
九宫之义,法以灵龟,
二四为肩,六八为足,
左七右三,戴九履一,
五居中央(如图6)。
朱熹在《易图》中也说“洛书盖取龟象,故其数戴九履一,左七右三,二四为肩,六八为足。”
方法四:有诗为证(如图7):
四海三山八仙洞(4,3,8),
九龙王子一枝莲(9,5,1),
二七六郎赏月半(2,7,6),
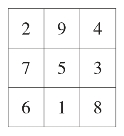
图6
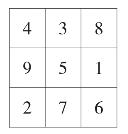
图7
周围十五月团圆(幻和15)。
三阶幻方虽然构造方法很多,但本质上是一种。不同的排法实际上是通过旋转、对称变换得到的。
三阶幻方也可以做一些推广。如对任意9个数组成的等差数列,都可以由1~9的每个数乘以X,再加Y,得到。
继续按照原先的从小到大的顺序排列,幻方仍然成立。
例如要用6、9、12、15、18、21、24、27、30构造三阶幻方:
把1~9构成的3阶幻方的每个数乘以3,再加3就可得到要求的幻方。
如图8,其中,幻和=54。
幻方也是一种中国传统游戏。
幻方的种类很多,但构造起来还是比较困难的。下面我们分别介绍几种常见的、特殊的幻方构造方法。
4.四阶幻方的构造
方法一:对角线倒排法。如图9,先把数字1~16按顺序填入四方格内,只需把两对角线的数字排列顺序颠倒一下即可,如主对角线上的1,6,11,16,换成16,11,6,1,副对角线也如法操作即可。
如图10即为一个四阶幻方,幻和是34。
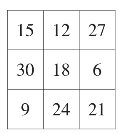
图8
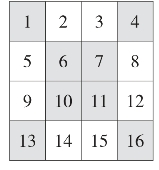
图9
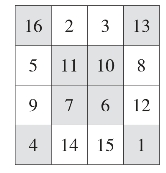
图10
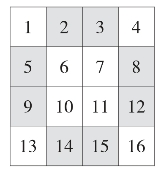
图11
方法二:中心对称交换法。如图11,先把1~16个数字按顺序填入四方格内,(2,15)、(3,14)、(5,12)、(9,8)关于中心对称,相互交换位置即得一个四阶幻方,如图12。
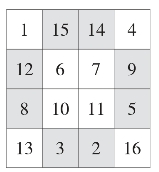
图12
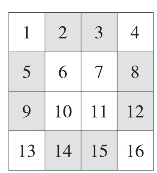
图13
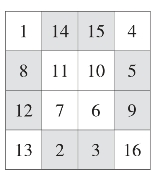
图14
方法三:平行对称法。如图13,先把数字1~16按如下顺序填入四方格内,则2,3与14,15关于横向轴对称;6,7与10,11也横向对称,类似的还有纵向对称。平行交换其位置即可得一个四阶幻方,如图14。
5.五阶幻方的构造
方法一:杨辉构造法。杨辉是我国古代著名的数学家和数学教育家,南宋钱塘人。杨辉对“九宫图”也就是三阶幻方进行了深入的研究,并把它命名为《纵横图》,并从三阶推广到高阶,取得了一系列重要的成果。

图15

图16
杨辉的方法是:二十五子斜排(如图15),上下对易(1与25,6与24,2与20交换),左右相更(同上,如图16),四维挺进(24、20挺进,25插入12与8中间,其余三维同法操作),即得到一个五阶幻方(如图17)。

图17 杨辉构造法
同样,用杨辉构造法,也可以类似地排出四阶幻方,方法如下(如图18):

图18
注意:中间虚线正方形内的数字也要进行上下对易、左右相更的变换。
方法二:劳伯尔构造法。
首先,把1放入第一行正中央的方格内,依次向右上方格內填入2,3,4,…,25。如果要填的数字的方格上出框,则往最下填(如2),右出框则往最左边放(如4),如果右上方已有数字,则在原方格向下移一格继续填(如6),依次填满25格。即可得到一个五阶幻方(如图19)。
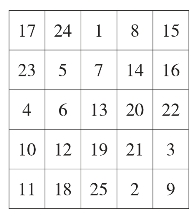
图19 劳伯尔构造法
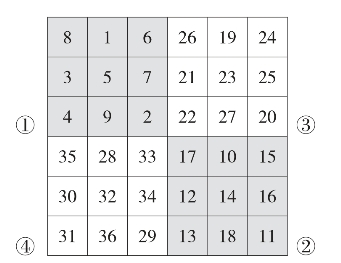
图20
此两种构造方法对奇数阶幻方均可适用。
6.六阶幻方的构造
方法一:我们可以把六阶大方阵分解为4个三阶子方阵,如图20。
按上述奇数阶幻方给出的劳伯尔构造法,分别给4个子方阵对应赋值。
子方阵由小到大依次为上左子阵①,下右子阵②,上右子阵③,下左子阵④。
4个子方阵对应的元素相差9,如上左子阵①第一行中间的数是1,下右子阵②第一行中间的数就是10,上右子阵③第一行中间的数是19,下左子阵④第一行中间的数是28,此时每一列的和均为幻和111(如图20),然后只需在同一列作对应元素的适当交换,交换原则使行列及对角线上元素之和均为111,由此得到六阶幻方(如图21)。
方法二:仿照四阶幻方的对角线倒排法。如图22,先把1~36个数字按顺序填入六六方格内,然后把两对角线的数字排列顺序颠倒一下,再根据幻和是111,分别对行、列进行一个微调即可完成六阶幻方(如图23)。

图21
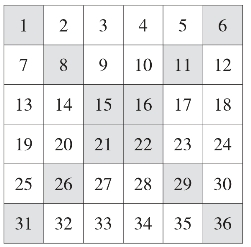
图22
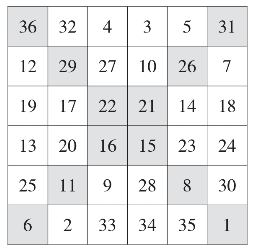
图23
更高阶的幻方,均可以仿照类似的方法来构造。
通过对幻方的研究,可以证明,二阶幻方是不存在的。三阶幻方本质上也只有一种。但四阶幻方就有880种,五阶幻方有2亿多种,而八阶幻方已超过10亿种。可见幻方的魅力还是很大的。
据记载,目前已经排出了125阶幻方。
7.其他幻方
(1)反幻方:在一个由若干个排列整齐的数组成的正方形中,图中任意一横行、一纵行及对角线的几个数之和都不相等,具有这种性质的图表,称为“反幻方”。
反幻方与正幻方最大的不同点是幻和不同,正幻方所有幻和都相同,而反幻方所有幻和都不同。如图24就是一个三阶反幻方。
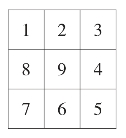
图24
(2)清末民初数学家寿孝天构造的“六六幻方”:
①每行、每列及两条对角线上的六个数之和都是111。
②“二次幻方”。第一行和第六行六个数字的平方和是相等的,都是3095。第一列和第六列也是如此,平方和等于2947。这是这块“六六幻方”非常独特的地方。
③“回整幻方”。去掉“六六幻方”最外一层数字,剩下部分是一个四阶幻方(如图25阴影部分),其每行、每列及两条对角线上的4个数之和都是74。
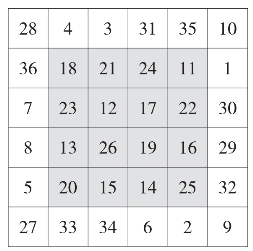
图25 六六幻方
④“完美幻方”。上述四阶幻方各条“泛对角线”上的4个数之和也都是74。例如,23+26+14+11,15+19+22+18,23+21+14+16等。
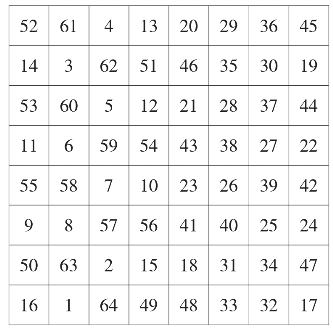
图26
(3)美国科学家富兰克林的8阶幻方(如图26):
这个八阶幻方,它也有一些独特的性质:
①幻方中的64个数字是从1至64,幻和是260。
②每半行、半列上各数和分别相等,均为半幻和130。
③幻方四个角上的四个数与最中心的四个数的和也等于幻和值260,即:52+45+16+17+54+43+10+23=260。
④从16到10,再从23到17所成折线“∧”上八个数字之和也为260;且平行这种折线的诸折线“∧”上的八个数字和也为260。
(4)魔鬼幻方
如将幻方看成是无限伸展的图形,则任何一个相邻的n×n方格内的数字都可以组成一个幻方。则称该幻方为魔鬼幻方。如图27的幻方更是魔鬼幻方,因为对于任意四个在相邻两行两列上的数字,他们的和都是34。如第一行、第二行、第二列、第三列上的四个数字是10,3,5,16,则10+3+5+16=34。
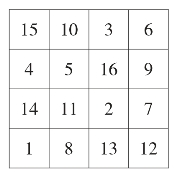
图27
(5)十二阶完美幻方:幻和是858,而且每个2*2的子矩阵其和均为286。
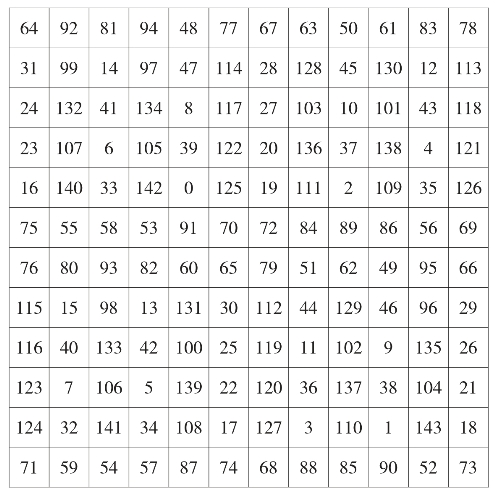
图28
(6)杨辉聚九图
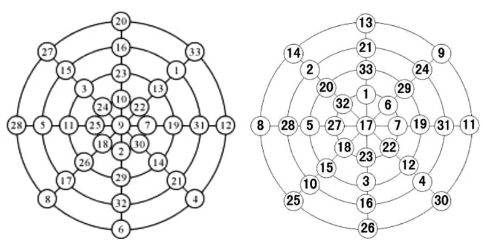
图29
说明:图29中的数字由1,2,3,4,…,33组成,其构成性质有:
①四个同心圆上的八个数字之和均相等;
②四条直径上的数字之和也相等;
③八条半径上的数字之和也相等;
④四条直径若去掉中心数(如9),其和与同心圆周上的数字之和也相等。
(7)六角幻方
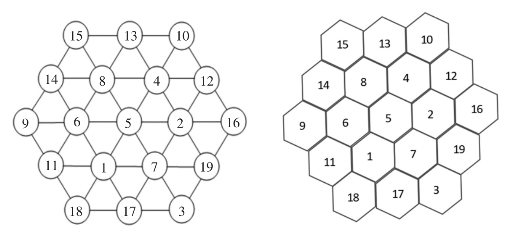
图30
1910年,美国有一位名叫阿当斯的铁路公司阅览室青年职员,对六角幻方很感兴趣,他排出了一个由1~19个数组成的3阶六角幻方(如图30)。
他一有空闲时间,便在纸上或地上画六角图,再把19块上面写有1到19这19个数的硬纸板在图上摆来摆去。就这样,一天又一天,一年又一年,漫漫的47个春秋过去了,这时的阿当斯已成了两鬓斑白的老人。面对无数次的失败与挫折,阿当斯的兴趣依然不减。1957年的一天,患病在床的阿当斯终于排列成功了。他连忙找纸把它记录下来,不幸的是,当他病愈出院回到家中时,却发现那张记录六角幻方的纸竟不见了。阿当斯并不因此灰心丧气,又奋斗了5年后,在1962年12月的一天,重新找到了那个丢失的图形。这个图形有个奇特的性质,就是横的五行及斜的十行上各自数字的和都是38。阿当斯对于耗费自己毕生心血而得来的六角幻方视如珍宝,并把它拿给幻方专家马丁·加德纳鉴赏。面对这巧夺天工的珍宝,马丁·加德纳博士顿感眼界大开,并为此写信给智慧超群的数学游戏专家特里格。特里格惊奇万分并深受鼓舞,决心在阿当斯六角幻方的基础上,对层数作出突破。他经过反复研究,终于惊奇地发现:三阶以上的六角幻方根本不存在。这就是说,普通的幻方可能有千千万万种排法,但六角幻方却只能有阿当斯这一个。
有关幻方的研究,不只是数学家、数学爱好者的一种智力游戏,其中也包含了一定的数学知识和对数学思维的训练,也是对人们智力的一种挑战。因此,人们研究幻方的热情总是不减。































