三角形内角和可以不是180度
在我们学过的平面几何中,我们都知道以下定理:
(1)三角形内角和是180°;
(2)过直线外一点只能作唯一一条直线和已知直线平行;
(3)与已知直线等距离且在该直线同侧的三点在同一直线上;
(4)同一直线的垂线和斜线必相交;
(5)存在两个相似而不全等的三角形;
(6)任意三角形存在一个外接圆,等等。
在大家看来这些命题是无可非议的,结论肯定是正确的。但这些只能是建立在欧氏几何体系里的结论,如果用非欧几何来衡量,这些结论就不一定是正确的。也就是说在非欧几何里,三角形的内角和可以小于180度,三角形内角和还可以大于180度等。
我们先来看看欧几里得与欧氏几何。
欧几里得(希腊文:Ευκλειδηζ,公元前330年—公元前275年),古希腊著名的数学家、欧氏几何学的开创者。

欧几里得画像
欧几里得(Euclid)出生于雅典,当时的雅典就是古希腊文明的中心,浓郁的文化气氛深深地感染了欧几里得,当他还是个十几岁的少年时,就迫不及待地想进入柏拉图学园学习。一天,一群年轻人来到位于雅典城郊外林荫中的柏拉图学园,只见学园的大门紧闭着,门口挂着一块木牌,上面写着:“不懂几何者,不得入内!”这是当年柏拉图亲自立下的规矩,为的是让学生们知道他对数学的重视,然而却把前来求教的年轻人给闹糊涂了。有人在想,正是因为我不懂数学,才要来这儿求教的呀,如果懂了,还来这儿做什么?正在人们面面相觑,不知是进是退的时候,欧几里得从人群中走了出来,只见他整了整衣冠,看了看那块牌子,然后果断地推开了学园大门,头也没有回地走了进去。
从此,欧几里得刻苦钻研,最终成了亚历山大大学的一个著名教授。亚历山大大学是希腊文化最后集中的地方,这个大学也是当时全世界最优秀的大学。欧几里得最著名的著作就是《几何原本》,这大概是一个课本,书中提出了著名的五大公理,并建立了系统、严谨的几何学体系,被后人称为欧氏几何,欧几里得也因此被称为“几何之父”。
几何学最早兴起于公元前7世纪的古埃及,后经古希腊等人传到古希腊的都城,又借毕达哥拉斯学派系统奠基,已经积累了许多几何学的知识。然而这些知识当中,存在一个很大的缺点和不足,就是缺乏系统性,大多数只是片断的、零碎的知识。公理与公理之间、证明与证明之间并没有什么很强的联系性,更不要说对公式和定理进行严格的逻辑论证和说明。
但是,随着社会经济的繁荣和发展,特别是随着农林畜牧业的发展、土地开发和利用的增多,把这些几何学的知识加以条理化和系统化,成为一整套可以自圆其说、前后贯通的知识体系,已经是刻不容缓,并成为科学进步的大势所趋。
正是在这样的背景下,欧几里得通过早期对柏拉图数学思想,尤其是几何学理论系统而周详的研究,已敏锐地察觉到了几何学理论的发展趋势。他下定决心,要在有生之年完成这一工作,成为系统几何第一人。为了完成这一重任,欧几里得不辞辛苦,长途跋涉,从爱琴海边的雅典古城,来到尼罗河流域的埃及新埠——亚历山大城,为的就是在这座新兴的、文化蕴藏丰富的异域城市来实现自己的初衷。在此地的无数个日日夜夜里,他一边收集以往的数学专著和手稿,向有关学者请教,一边试着著书立说,阐明自己对几何学的理解。经过欧几里得忘我的劳动,终于在公元前300年结出丰硕的果实,这就是几经易稿而最终定形的《几何原本》一书。这是一部传世之作,几何学正是有了它,不仅第一次实现了系统化、条理化,而且又孕育出一个全新的研究领域——欧几里得几何学,简称欧氏几何。直到今天,欧几里得所创作的《几何原本》仍然是世界各国学校里的必修课,从小学、初中、大学,再到现代高等学科都有他所创作的定律、理论和公式的应用。
《几何原本》是一部集前人思想和欧几里得个人创造性于一体的不朽之作。这部书已经基本囊括了几何学从公元前7世纪的古希腊,一直到公元前4世纪,前后总共400多年的数学发展历史。它不仅保存了许多古希腊早期的几何学理论,而且通过欧几里得开创性的系统整理和完整阐述,使这些远古的数学思想发扬光大。它也开创了古典数论的研究,在一系列公理、定义、公设的基础上,创立了欧几里得几何学体系,使其成为用公理化方法建立起来的数学演绎体系的最早典范。
按照欧氏几何学的体系,所有的定理都是从一些确定的、不需证明而礴然为真的基本命题即公理演绎出来的。在这种演绎推理中,对定理的每个证明必须或者以公理为前提,或者以先前就已被证明了的定理为前提,最后做出结论。
全书共分13卷。书中包含了5条“公理”,5条“公设”,23个定义和467个命题。在每一卷内容当中,欧几里得都采用了与前人完全不同的叙述方式,即先提出公理、公设和定义,然后再由简到繁地证明它们。这使得全书的论述更加紧凑和明快。而在整部书的内容安排上,也同样贯彻了他的这种独具匠心的安排。它由浅到深,从简至繁,先后论述了直边形、圆、比例论、相似形、数、立体几何以及穷竭法等内容,其中有关穷竭法的讨论,成为了近代微积分思想的来源。
欧几里得使用的公理化的方法,后来成了建立任何知识体系的典范,在差不多两千年间,被奉为必须遵守的严密思维的范例。
藏于牛津大学自然历史博物馆的《几何学发展概要》中,就记载着这样一则故事,说的是数学在欧几里得的推动下,逐渐成为人们生活中的一个时髦话题,以至于当时亚里山大国王托勒密一世也想赶这一时髦,准备学点几何学。虽然这位国王见多识广,但欧氏几何却令他学得很吃力。于是,他问欧几里得“学习几何学有没有什么捷径可走?”,欧几里得笑道:“抱歉,陛下!学习数学和学习一切科学一样,是没有什么捷径可走的。学习数学,人人都得独立思考,就像种庄稼一样,不耕耘是不会有收获的。在这一方面,国王和普通老百姓是一样的。”从此,“在几何学里,没有专为国王铺设的大道。”这句话成为了千古传诵的学习箴言。
还有一则故事。那时候,人们建造了高大的金字塔,可是谁也不知道金字塔究竟有多高。有人这么说:“要想测量金字塔的高度,比登天还难!”这话传到欧几里得耳朵里。他笑着告诉别人:“这有什么难的呢?当你的影子跟你的身体一样长的时候,你去量一下金字塔的影子有多长,那长度便等于金字塔的高度!”
来拜欧几里得为师,学习几何的人,越来越多。有的人是来凑热闹的,看到别人学几何,他也学几何。有一位学生曾这样问欧几里得:“老师,学习几何会使我得到什么好处?”欧几里得思索了一下,请仆人拿点钱给这位学生。欧几里得说:给他三个钱币,因为他想在学习中获取实利。
欧几里得是古希腊最负盛名、最有影响的数学家之一。欧几里得的《几何原本》对于几何学、数学和科学的未来发展,对于西方人的整个思维方法都有极大的影响,《几何原本》是古希腊数学发展的顶峰。欧几里得将几何整理在严密的逻辑系统运算之中,使几何学成为一门独立的、演绎的科学。欧几里得的《几何原本》,被广泛认为是历史上最成功的教科书,也是欧洲数学的基础。
欧几里得还写了一些关于透视、圆锥曲线、球面几何学及数论的作品。除了《几何原本》之外,他还有不少著作,可惜大都失传。欧几里得流传至今还有另外五本著作。如《已知数》《圆形的分割》《反射光学》《现象》《光学》等,它们与《几何原本》一样,内容都包含定义、定理及证明。
欧几里得在《几何原本》中为推演出几何学的所有命题,一开头就给出了五个公理(适用于所有科学)和五个公设(只应用于几何学),作为逻辑推演的前提。
五个公理是:
用数学语言来描述就是(设a,b,c,d皆为正数):
(1)与同一个量相等的两个量相等;即若a=c且b=c,则a=b(等量代换公理)。
(2)等量加等量和相等;即若a=b且c=d,则a+c=b+d(等量加法公理)。
(3)等量减等量差相等;即若a=b且c=d,则a-c=b-d(等量减法公理)。
(4)完全重合的两个图形是全等的(全等公理)。
(5)全量大于分量,即a+b>a(全量大于分量公理)。
五个公设,用现代语言描述就是:
(1)过相异两点,能作且只能作一条直线(直线公理)。
(2)任意线段能无限延伸成一条直线(线段公理)。
(3)给定任意线段,可以以其一个端点为圆心,以该线段长为半径作一个圆(圆公理)。
(4)凡是直角都相等(角公理)。
(5)两条直线被第三条直线所截,如果同侧两内角(同旁内角)和小于两个直角,则这两条直线在这一边必定相交(平行公理)。
《几何原本》的注释者和评述者们对五个公理和前四个公设都是很满意的,也没有什么异议,唯独对第五个公设(即平行公理)提出了质疑。
第五公设是论及平行线的。它说的是:“如果一直线和两直线相交,且所构成的两个同旁内角之和小于两直角,那么,把这两直线延长,它们一定在那两内角的一侧相交。”数学家们并不怀疑这个命题的真实性,而是认为它无论在语句的长度,还是在内容上都不大像是个公设,而倒像是个可以证明的定理,只是由于欧几里得没能找到它的证明,才不得不把它放在公设之列。
后来人们又给出了第五公设的等价命题——普列菲尔公理:
“过平面上直线外一点,只能引一条直线与已知直线不相交(平行)。”
为了给出第五公设的证明,完成欧几里得没能完成的工作,自公元前 3世纪起到 19 世纪初的 1800 年间,数学家们投入了无穷无尽的精力,试图都尝试用欧几里得几何中的其他公理来证明欧几里得的平行公理,还尝试了各种可能的方法,但是结果都归于失败。
19 世纪,德国数学家高斯、俄国数学家罗巴切夫斯基、匈牙利数学家波尔约等人各自独立地认识到 这种证明是不可能的。也就是说,平行公理是独立于其 他公理的,并且 可以用不同的“平行公理”来 替代它 ,这也就 是 后来产生的非欧几何。
高斯关于非欧几何研究的信件和笔记在他生前一直没敢公开发表,只是在他 1885 年去世后,后人在整理高斯遗著出版时才引起了人们的注意。
但是,俄国数学家罗巴切夫斯基,就大胆地否定欧氏的第五公设,提出
“过平面上直线外一点,至少可引两条直线与已知直线不相交。”
也就是说三角形内角和可以小于 180 度,并由此可以建立一个全新的非欧几何体系。

罗巴切夫斯基
尼古拉斯·伊万诺维奇·罗巴切夫斯基(Никола й Ива нович Лобаче вский, 英 文 Nikolas lvanovich Lobachevsky,1792 年 12 月 1 日—1856 年 2 月 24 日),俄罗斯数学家,非欧几何的早期发现人之一。罗巴切夫斯基于 1807 年进入喀山大学,1811 年获得物理数学硕士学位,并留校工作,1814 年任教授助理,1816 年升为额外教授,1822 年成为常任教授。1827 年,大学校委会选举他担任喀山大学校长,1846 年以后任喀山学区副督学,直至逝世。
罗巴切夫斯基在尝试证明平行公理时发现以前所有的证明都无法逃脱循环论证的错误。于是,他作出假定:过直线外一点,可以作无数条直线与已知直线平行。如果这假定被否定,则就证明了平行公理。然而,他不仅没有能否定这个命题,而且用它同其他欧氏几何中与平行公理无关的命题一起展开推论,得到了一个逻辑关系合理的新的几何体系——非欧几里得几何学,这就是后来人们所说的罗氏几何。
依照这个逻辑思路,罗巴切夫斯基对第五公设的等价命题“过平面上直线外一点,只能引一条直线与已知直线不相交”作以否定,得到的否定命题就是:
“过平面上直线外一点,至少可引两条直线与已知直线不相交。”
罗巴切夫斯基把它作为一条新的公理,并在推演过程中,得到一连串古怪、非常不合乎常理的命题,如:
(1)任意三角形的内角和小于180°;
(2)平面上一直线的垂线和斜线不一定相交;
(3)相似而不全等的三角形不存在;
(4)存在无外接圆的三角形;
(5)在平面上与已知直线等距离且在该直线同侧的点的轨迹是一曲线,它上面的任何三点不在同一直线上,等等。
罗巴切夫斯基经过仔细审查,却没有发现它们之间存在任何逻辑矛盾。于是,远见卓识的罗巴切夫斯基大胆断言,这个“在结果中并不存在任何矛盾”的新公理系统可构成一种新的几何,它的逻辑完整性和严密性可以和欧几里得几何相媲美。而这个无矛盾的新几何的存在,就是对第五公设可证性的反驳,也就是对第五公设不可证性的逻辑证明。由于尚未找到新几何在现实世界的原型和类比物,罗巴切夫斯基慎重地把这个新几何称之为“想象几何”。
1826年2月23日,罗巴切夫斯基于喀山大学物理数学系学术会议上,宣读了他的第一篇关于非欧几何的论文:《几何学原理及平行线定理严格证明的摘要》,在这篇论文里,罗巴切夫斯基用自己的“平行公理”替代了欧几里得的平行公理,即在一个平面上,过已知直线外一点至少有两条直线与该直线不相交,并由此可演绎出一系列全无矛盾的结论,如三角形的内角和小于两直角等许多不同于欧氏几何的定理。这篇首创性论文的问世,标志着非欧几何的诞生。
罗巴切夫斯基几何的公理系统和欧几里得几何不同的地方仅仅是否定了欧式几何的平行公理,其他公理基本相同。由于平行公理的不同,经过演绎推理却引出了一连串和欧式几何内容不同的新的几何命题。
在罗氏几何中,除了一个平行公理之外,其余全采用了欧式几何的一切公理。因此,凡是不涉及平行公理的几何命题,在欧式几何中如果是正确的,在罗氏几何中也同样是正确的。
在欧式几何中,凡涉及平行公理的命题,在罗氏几何中都不成立,他们都相应地含有新的意义。所以罗氏几何中的一些几何事实没有像欧式几何那样容易被接受。所以,这一重大成果刚一公之于世,就遭到正统数学家的冷漠和反对。
在创立和发展非欧几何的艰难历程上,罗巴切夫斯基始终没能遇到他的公开支持者,就连非欧几何的另一位发现者德国的大数学家高斯也不肯公开支持他的工作。但是罗巴切夫斯基勇敢地面对研究非欧几何带来的怀疑、嘲笑,甚至是不断的打压,他坚持真理,坚持自己对非欧几何的发现、研究和传播。
后来,数学家们又经过研究,提出可以用我们习惯的欧式几何中的事实作一个直观“模型”来解释罗氏几何是正确的。如图1中在双曲面上的几何图形就可以解释罗氏几何。
罗氏几何的创立对几何学和整个数学的发展起了巨大的作用,虽然一开始并没有引起重视,直到罗巴切夫斯基去世12年后才逐渐被广泛认同。但是罗巴切夫斯基的独创性研究和对非欧几何的贡献,后来也得到了学术界的高度评价和一致赞美,这时的罗巴切夫斯基已经被人们赞誉为“几何学中的哥白尼”。
在科学探索的征途上,一个人经得住一时的挫折和打击并不难,难的是勇于长期甚至终生在逆境中奋斗。罗巴切夫斯基就是在逆境中奋斗终生的勇士。
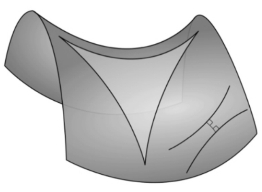
图1
继罗氏几何后,德国数学家黎曼在1854年又提出了既不是欧氏几何也不是罗氏几何的新的非欧几何。

黎曼
波恩哈德·黎曼(公元1826—1866),是德国著名的数学家,他在数学分析和微分几何方面作出过重要贡献,他开创了黎曼几何,并且给后来爱因斯坦的广义相对论提供了数学基础。
这种几何采用了如下的公理替代欧几里得平行公理:
同一平面上的任何两直线一定相交。
同时,还对欧氏几何的其他公理做了部分改动,在这种几何里可以得到:
三角形的内角和大于180度。
人们把这种几何称为椭圆几何或黎曼几何。
黎曼是在1851年所作的一篇论文《论几何学作为基础的假设》中明确地提出另一种几何学的存在,由此开创了几何学的另一片新的广阔领域,创立了黎曼几何学。
黎曼几何中的一条基本规定是:在同一平面内任何两条直线都有公共点。在黎曼几何学中不承认平行线的存在。
它的另一条公设是:直线可以无限延长,但总的长度是有限的。黎曼几何的模型就是一个经过适当“改进”的球面,所以黎曼几何又称椭圆几何。
附:黎曼几何、罗氏几何、欧氏几何模型图(如图2):

图2
在近代,黎曼几何在广义相对论里得到了重要的应用,尤其是在物理学家爱因斯坦的广义相对论中的空间几何就是黎曼几何。在广义相对论里,爱因斯坦放弃了关于时空均匀性的观念,他认为时空只是在充分小的空间里以一种近似性而均匀的,但是整个时空却是不均匀的,在物理学中的这种解释,恰恰与黎曼几何的观念是相似的。
此外,黎曼几何在数学中也是一个重要的工具。它不仅是微分几何的基础,也应用在微分方程、变分法和复变函数论等方面。
黎曼是世界数学史上最具独创精神的数学家之一,黎曼的著作不多,但却异常深刻,极富于对概念的创造与想象。他对偏微分方程及其在物理学中的应用有重大贡献。甚至对物理学本身,如对热学、电磁非超距作用和激波理论等也作出重要贡献。
黎曼的工作直接影响了19世纪后半期的数学发展,许多杰出的数学家重新论证黎曼断言过的定理,在黎曼思想的影响下数学许多分支取得了辉煌成就。
以他的名字命名的众多数学概念如:黎曼ζ函数,黎曼积分,黎曼引理,黎曼流形,黎曼空间,黎曼映照定理,黎曼-希尔伯特问题,柯西-黎曼方程,黎曼思路回环矩阵等出现在各种数学教科书中。
非欧几何是人类认识史上一个富有创造性的伟大成果。它的创立,不仅带来了近百年来数学的巨大进步,而且对现代物理学、天文学以及人类时空观念的变革都产生了深远的影响。
非欧几何的产生与发展,在客观上对研究了2000多年的第五公设作了总结,它引起了人们对数学本质的深入探讨,影响着现代自然科学、现代数学和数学哲学的发展:
其一,随着非欧几何的产生,引起了数学家们对几何基础的研究,从而从根本上改变了人们的几何观念,扩大了几何学的研究对象,使几何学的研究对象由图形的性质进入到抽象空间,即更一般的空间形式,使几何的发展进入了一个以抽象为特征的崭新阶段。可以说,非欧几何的产生是数学以直观为基础的时代进入以理性为基础的时代的重要标志。
其二,非欧几何的产生,引起了一些重要数学分支的产生。数学家们围绕着几何的基础问题、几何的真实性问题或者说几何的应用可靠性问题等的讨论,在完善数学基础的过程中,相继出现了一些新的数学分支,如数的概念、分析基础、数学基础、数理逻辑等,公理化方法也获得了进一步的完善。
其三,非欧几何学的创立为爱因斯坦发展广义相对论提供了思想基础和有力工具,而相对论给物理学带来了一场深刻的革命,动摇了牛顿力学在物理学中的统治地位,使人们对客观世界的认识产生了质的飞跃。
其四,非欧几何学使数学哲学的研究进入了一个崭新的历史时期。18世纪和19世纪前半期最具影响的康德哲学,它的自然科学基础支柱之一是欧几里得空间。非欧几何的创立,冲破了传统观念并破除了千百年来的思想习惯,给康德的唯心主义哲学以有力一击,使数学从传统的形而上学的束缚下解放出来,用康托尔的话说“数学的本质在于其自由”。
非欧几何也不是一蹴而就的,每一个重大问题的解决,往往需要许多代人的共同努力,才能取得成功,而后人总是“站在前人的肩膀上”的。




