没有规矩不成方圆
俗话说,没有规矩不成方圆。也就是说,作圆必须用圆规,如果没有圆规或没有画圆的工具就不能作圆。同样,作方也就是作矩形或正方形等必须用直尺和圆规,没有直尺同样做不出矩形和正方形。此话后来的意思已经映射到做人做事,意为一个人如果没有规矩(不遵守规则),就不能成为一个有用的人,它告诉我们一个重要的道理——做任何事都要有规矩,懂规矩,守规矩。
“不以规矩,不能成方圆”出自《孟子》的《离娄章句上》,孟子要求当政者要实施仁政。具体落实到两个方面,一是“法先王”,二是“选贤才”。所以“不以规矩,不能成方圆”的说法成为了人们在生活中常用的格言警句。
而数学中用直尺和圆规作图是几何学的重要内容之一。数学中的很多图形都可以用直尺和圆规作出,如三角形、四边形、多边形、圆以及部分正多边形等。
凡是能用直尺(这里指无刻度的直尺)和圆规作出的图形,都称为尺规图形,其作图过程就叫做尺规作图。
尺规作图是起源于古希腊的重要数学课题。古希腊时的数学比较发达,古希腊人比较重视规、矩在数学中训练思维和智力的作用,而不太重视规矩的实用价值。因此,在作图中对规、矩的使用方法加以很多限制,提出了尺规作图问题。所谓尺规作图,就是指有限次地使用没有刻度的直尺和圆规进行作图。
古希腊的哲学家安那萨哥拉斯首先提出作图要有尺规限制。他因政治上的纠葛,被关进监狱,并被判处死刑。在监狱里,他思考改圆成方以及其他有关问题,用来打发令人苦恼的无所事事的监狱生活。他不可能有规范的作图工具,只能用一根绳子画圆,用随便找来的破木棍作直尺,当然这些尺子上不可能有刻度。另外,对他来说,时间是不多了,因此他很自然地想到要有限次地使用尺规来解决问题。后来以理论的形式具体明确这个规定的是欧几里得的《几何原本》。
尺规作图的两点基本要求:
(1)直尺必须没有刻度,无限长,且只能使用直尺的固定一侧。只可以用它来将两个点连在一起,并且只准许使用有限次;
(2)圆规可以开至无限宽,但上面亦不能有刻度。它只可以拉开成之前构造过的长度。
当然,尺规作图也有严格的定义和要求。
基于“作图公法”的定义如下:
承认以下五项前提,有限次运用以下五项公法而完成的作图方法,就是合法的尺规作图:
五项前提是:
(1)允许在平面上、直线上、圆弧线上已确定的范围内任意选定一点(所谓“确定范围”,依下面的四条规则);
(2)可以判断同一直线上不同点的位置次序;
(3)可以判断同一圆弧线上不同点的位置次序;
(4)可以判断平面上一点在直线的哪一侧;
(5)可以判断平面上一点在圆的内部还是外部。
尺规作图的基本方法,也称为作图公法,任何尺规作图的步骤均可分解为以下五种方法:
(1)通过两个已知点可作一条直线;
(2)已知圆心和半径可作一个圆;
(3)若两已知直线相交,可求其交点;
(4)若已知直线和一已知圆相交,可求其交点;
(5)若已知两圆相交,可求其交点。
八种基本作图:
(1)作一条线段等于已知线段;
(2)作一个角等于已知角;
(3)作已知线段的垂直平分线;
(4)作已知角的角平分线;
(5)过一点作已知直线的垂线;
(6)已知一角、一边作等腰三角形;
(7)已知两角、一边作三角形;
(8)已知一角、两边作三角形。
下面来看尺规作图中的两个最著名的问题:
1.尺规作正多边形
在各种图形中,正多边形是大家比较感兴趣的一类。由于圆规可以画圆,而所有正多边形都可以内接于圆,因此它的所有顶点都在圆周上。这样看来,正多边形应该很有希望用尺规作图。而且,前几个正多边形的作图方法很快就构造出来了,步骤也不算复杂,如正三角形、正四边形、正五边形、正六边形、正八边形等。然而还是有很多正多边形没有找到尺规作图的方法,如正七边形、正九边形等。人们自然要问,是否存在不可能尺规作图的正多边形?
相对于同时期的其他文明,古希腊数学更富思辨精神。尽管当时的数学问题都是源于生活,但古希腊人并不立足于解决生活问题,而是考虑一般的理想情形。边数较多的多边形在实际问题中几乎不会出现,但他们仍然对这些多边形的尺规作图很感兴趣,并且还执着地规定直尺不能带刻度。
那么,只使用直尺和圆规,可以做哪些正多边形呢?又不能做哪些正多边形呢?
如我们已经作过的正四边形、正五边形、正六边形等。
只使用直尺和圆规,能否作出正七边形?这个看上去非常简单的题目,曾经使许多著名数学家都束手无策,最终证明,正七边形是不能由尺规作出的。
同样,只使用直尺和圆规,作正九边形也不能作出来,因为单用直尺和圆规,是不足以把一个角分成三等份的。
那么,只使用直尺和圆规,到底可以作出哪些正多边形呢?
用尺规作正偶边形如4,6,8,10,12等正多边形并非难事,但做正14边形、18边形就比较困难。对于正奇边形如7,9,11,13,15等的作图,在当时也是件困难的事,而且并非全都可以用尺规作图。
这个问题在经过漫长的两千多年后,才最终被天才的数学家高斯在24岁时完全解决。1798年,德国数学家高斯只有19岁,在读大学二年级时就给出了正十七边形的尺规作图法的依据,并且在24岁时还给出了可用尺规作图的正多边形的条件:“能用尺规作出的正多边形,其边数目必须是2的非负整数次幂和不同的费马素数的积”(费马素数是指形如F(n)=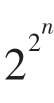 +1的质数,其中n是非负整数),这才解决了两千年来悬而未决的难题。
+1的质数,其中n是非负整数),这才解决了两千年来悬而未决的难题。
高斯虽然给出了判断方法,但高斯本人实际上并不会做正十七边形。第一个真正的正十七边形尺规作图法直到1825年才由约翰尼斯·厄钦格(Johannes Erchinger)给出。当高斯去世后,人们为了纪念这位伟大的数学家,在他的纪念碑上刻了一个正17边形(一说是刻了一个正十七角形)。
对于费马素数F(n)=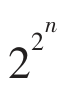 +1,只有当n=0,1,2,3,4时,
+1,只有当n=0,1,2,3,4时,
F=3,5,17,257,65537。
它们都是质数,但一般猜测n>4时,费马数都不是质数(现在也只是猜想)。如n=5时,F5=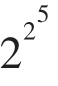 +1=232+1=4294967297=641×6700417就不是质数。
+1=232+1=4294967297=641×6700417就不是质数。
根据高斯的结论,一个正多边形可以尺规作图,当且仅当边数是费马素数或者两个不同的费马素数的乘积,或者是这些数的2的乘幂倍(即2倍,4倍,8倍,16倍,等)。高斯的结论给出的是一个充分必要条件,换句话说,费马素数的数量决定了能尺规作图的奇数边正多边形的个数。由于我们现在所知道的只有五个费马质数存在,所以用圆规可以作出的正奇边形是3,5,17,257,65537,以及这五个数的两两相乘的积。如3×5,3×17,5×17×257等共31个,而最大的正奇边形的边数是3×5×17×257×65537。
根据高斯的结论,边数小于100,可以用尺规作图的正多边形边数如下:
3,4,5,6,8,10,12,15,16,17,20,24,30,32,34,40,48,51,60,64,68,80,85,96(24个)。
不过,高斯的证明只是针对存在性,而没有给出具体的作图方法,包括著名的正十七边形的作法,也不是他亲自作出来的。
下面我们以正五边形为例,如图1,看看如何用尺规作出正五边形。
(1)在平面内作一圆,圆心为O;
(2)在圆O上取一点A,连接AO并延长交圆O于另一点B(假设令AB=4);

图1
(3)过点O作CD⊥AB,交圆O于C、D两点(此时CD=4);
(4)作OB的垂直平分线MN,交OB于E点,交圆O于M,N(此时OE=BE=1);
(5)以点E为圆心,EC长为半径作弧,交BO延长线于点F;(此时EC=EF=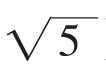 )
)
(6)以点B为圆心,BF长为半径作弧,交圆O分别于G、H两点
(此时BF=EF+BE=1+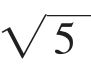 ,由此可知
,由此可知
cos∠ABG=(EF+BE)/AB=(1+ )/4=cos 36°,
)/4=cos 36°,
而∠AOG=2∠ABG=72°=360°/5(边所对的圆心角),
此时便得到了圆周上的五等份点的其中三个A、G、H。
(7)以点G为圆心,GA长为半径作弧,交圆O于P点;
(8)以点H为圆心,HA长为半径作弧,交圆O于Q点;
(9)连接AG、GP、PQ、QH、HA,则五边形AGPQH即为正五边形。
下面我们分别来看一下其他正多边形的作图过程。
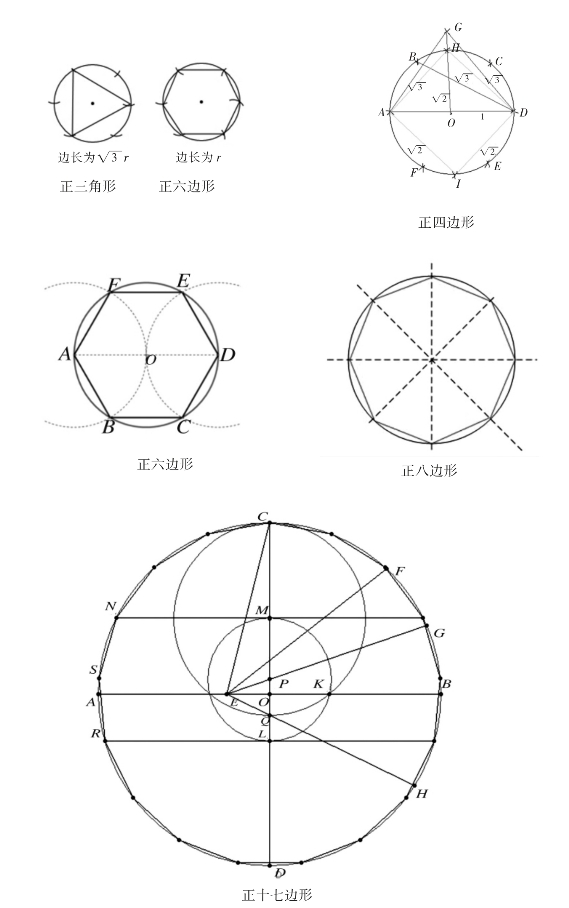
图2
由于,
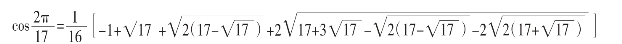
它是有理数的加、减、乘、除、平方根的组合,是无理数,但不是超越数,故正17边形可用尺规作出(高斯结论)。
作法:
(1)给一圆O,作两垂直的直径AB、CD;
(2)在OA上作E点,使OE=(1/4)AO,连结CE;
(3)作∠CEB的平分线EF交圆于F;
(4)作∠FEB的平分线EG,交CO于P;
(5)作∠GEH=45°,交CD于Q;
(6)以CQ为直径作圆,交OB于K;
(7)以P为圆心,PK为半径作圆,交CD于L、M;
(8)分别过M、L作CD的垂线,交圆O于N、R;
(9)作弧NR的中点S,以SN为半径就可将圆O分成17等份。
2.四等分圆周
只准许使用圆规,将一个已知圆心的圆周四等分。这个问题传言是拿破仑·波拿巴出的,曾向全法国的数学家挑战。
又说,此题目原是由意大利数学家罗兰索·马歇罗尼(Lorenzo Mascheroni)向拿破仑·波拿巴提出的,但不知道他是否有解出这个问题。此题目后来又更加进化,变成只给定一圆,不知道圆心,只用圆规将此圆四等分,在这种情况下,必须先用圆规作图找到圆心。
以上两种问题都被称为拿破仑问题。
第一个问题:已知一个圆,只用圆规找出其圆心。
作法(如图3):
(1)在已知圆上任取一点A,以A为圆心,适当长为半径作圆A,分别交已知圆于B,C两点;
(2)在圆A上,以AB的长为半径,从点B开始,逆时针依次画弧,截取弧BD,弧DE,弧EF;
(3)分别以F,A为圆心,以FC的长为半径画弧交于点G;
(4)再以G为圆心,以FC的长为半径画弧,交圆A于点H;
(5)分别以B,A为圆心,以BH的长为半径作弧,两弧交于点O,则点O就是要求作的已知圆的圆心。
若想证明点O就是圆心,只要证出点O到A,C,B三点的距离相等即可。
证明:由作法可知,△BAD,△AED,△EAF均为等边三角形,
则∠BAD+∠DAE+∠EAF=180°,
即点B,A,F三点共线。
又AG=FG=GH=FC,AF=AH,
则:△HAG≌△FAG(SSS),
所以,∠HAG=∠FAG;
又AB=AH,则∠ABH=∠AHB;
即∠FAH=2∠ABH,
由此可知∠FAG=ABH=∠AHB=∠HAG;
∴△FAG∽△BHA,AF/BH=AG/AB=FG/AH
又BO=AO=BH,FC=FG,
则:AF/BO=AC/AO=FC/AB,
得△AFC∽△OBA,∠FAC=∠BOA;
∴∠OAC=180°-∠FAC-∠BAO=180°-∠BOA-∠ABO=∠BAO;
又AB=AC,AO=AO,则△OAC≌△OAB(SAS);
得OC=OB=OA;
故点O为已知圆的圆心。
第二个问题:四等分圆周长。
这个问题也可以变形为:只用圆规,不许用直尺,在平面圆上构造四个点,使之成为某个正方形的顶点。当然这个问题后来被证明是有解的。
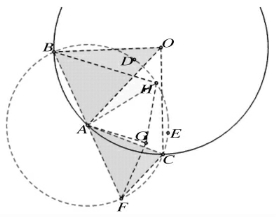
图3
思路:设半径为1。可算出其内接正方形边长为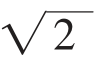 ,也就是说用这个长度去等分圆周即可,我们的任务就是作出这个长度。先作出六等份圆周,这时会出现一个
,也就是说用这个长度去等分圆周即可,我们的任务就是作出这个长度。先作出六等份圆周,这时会出现一个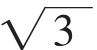 的长度。设法构造斜边为
的长度。设法构造斜边为 ,一直角边为1的直角三角形,
,一直角边为1的直角三角形,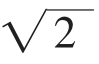 的长度自然就出来了。
的长度自然就出来了。
(1)如图4,取已知圆O上任一点A,以A为一个分点把⊙O六等分,分点依次为A、B、C、D、E、F;
(2)分别以A、D为圆心,AC、BD为半径作圆交于G(若设圆的半径为1,此时AC=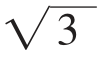 ,OG=
,OG=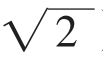 );
);
(3)以A为圆心,OG为半径作圆,交⊙O于M、N,则点A、M、D、N即四等分⊙O的圆周。
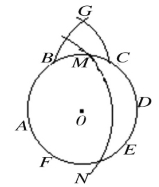
图4

图5
第三个问题:四等分圆的面积。
(1)如图5,以A为圆心,OA长为半径画弧,交⊙O于两点,取⊙O上在点A顺时针方向的点为点E;
(2)以E为圆心,OA长为半径画弧,把点O与点A用圆弧相连;
(3)以同样的方法作出弧OM、OD、ON,则这四条弧把⊙O的面积四等分。
在中国古代,对尺规作图也有一定的研究,并取得了突出的成绩。
“规”就是圆规,是用来画圆的工具,在我国古代甲骨文中就有“规”这个字。“矩”就像木工使用的角尺,由长短两尺相交成直角而成,两者间用木杠连接以使其牢固,其中短尺叫勾,长尺叫股。
矩的使用是我国古代的一个发明,山东历城武梁祠石室造像中就有“伏羲氏手执矩,女娲氏手执规”之图形。矩不仅可以画直线、直角,加上刻度可以测量,还可以代替圆规。甲骨文中也有矩字,这可追溯到大禹治水(公元前2000年)前。
《史记》卷二记载大禹治水时“左准绳,右规矩”。赵爽注《周髀算经》中有“禹治洪水,……望山川之形,定高下之势,……乃勾股之所由生也。”意即大禹治洪水,要先测量地势的高低,就必定要用勾股的道理。这也说明矩起源于很远的中国古代。
春秋时代也有不少著作涉及规矩的论述,《墨子》卷七中说“轮匠(制造车子的工匠)执其规矩,以度天下之方圆。”《孟子》卷四中说“离娄(传说中目力非常强的人)之明,公输子(即鲁班,传说木匠的祖师)之巧,不以规矩,不能成方圆。”可见,在春秋战国时期,规矩已被广泛地用于作图、制作器具了。由于我国古代的矩上已有刻度,因此使用范围较广,具有较大的实用性。
当然,也有很多几何作图问题是无法用尺规来完成的,称为“尺规作图不能问题”。
由于《几何原本》的巨大影响,希腊人所崇尚的尺规作图规则也一直被遵守并流传下来。由于对尺规作图的严格限制,使得一些貌似简单的几何作图问题却无法解决。
最著名的是被称为几何三大问题的三个古希腊古典作图难题:
这三大问题的具体内容为:
(1)立方倍积问题:作一个立方体,使它的体积是已知立方体体积的两倍;
(2)化圆为方问题:作一个正方形,使它的面积等于已知圆的面积;
(3)三等分任意角问题:作一个角,将其分为三个相等的部分。
以上三个问题在2400年前的古希腊就已被提出,当时很多有名的希腊数学家,都曾着力于研究这三大问题,但由于尺规作图的限制,却一直未能如愿以偿。以后两千多年来,无数数学家为之绞尽脑汁,都以失败而告终。直到1637年笛卡尔创立了解析几何,关于尺规作图的可能性问题才有了准则。直至1837年法国数学家万芝尔才首先证明“立方倍积”问题和“三等分任意角”问题都属于尺规作图不可能问题。而后在1882年德国数学家林德曼证明了π是超越数后,“化圆为方”问题也被证明为尺规作图不能问题,这才结束了历时两千年的数学难题公案。
几何三大作图难题虽然已经有了结论,但结论“不可能”,其前提是尺规作图。
如果不限于尺规,借助于其他工具或曲线,这三大难题就完全会成为可能。
比如引进抛物线,就可以作出“倍立方问题”。

图6
设已知立方体的棱长为a,体积为a3,则倍立方的体积为2a3,棱长为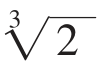 a。
a。
给出两条抛物线x2=ay和y2=2ax,如图6,设它们的交点为A,则A点的横坐标为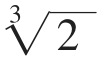 a,即OB=
a,即OB=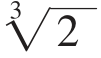 a,即为所求的倍立方的棱长。
a,即为所求的倍立方的棱长。
对于三等分角问题,指的是不能三等分“任意角”,对于某些特殊的角如90°,它就是可以三等分的。如果跳出尺规作图法则的限制,比如引入双曲线,则“三等分角”就是可能的。
再比如引入圆积线,也可以解决“化圆为方问题”。
总之,几何作图三大问题经历了两千余年,凝聚了无数数学家的心血,最终在解析几何工具下得到解决。
几何三大问题也促进了对圆锥曲线的研究,发现了一些有价值的特殊曲线,提出了尺规作图的判别准则,这些都比几何三大问题本身的意义深远得多。
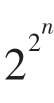 +1的质数,其中n是非负整数),这才解决了两千年来悬而未决的难题。
+1的质数,其中n是非负整数),这才解决了两千年来悬而未决的难题。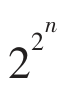 +1,只有当n=0,1,2,3,4时,
+1,只有当n=0,1,2,3,4时,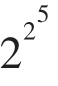 +1=2
+1=2
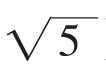 )
)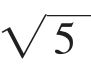 ,由此可知
,由此可知 )/4=cos 36°,
)/4=cos 36°,

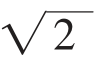 ,也就是说用这个长度去等分圆周即可,我们的任务就是作出这个长度。先作出六等份圆周,这时会出现一个
,也就是说用这个长度去等分圆周即可,我们的任务就是作出这个长度。先作出六等份圆周,这时会出现一个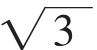 的长度。设法构造斜边为
的长度。设法构造斜边为 ,一直角边为1的直角三角形,
,一直角边为1的直角三角形,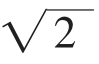 的长度自然就出来了。
的长度自然就出来了。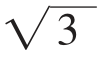 ,OG=
,OG=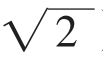 );
);


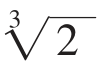 a。
a。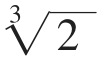 a,即OB=
a,即OB=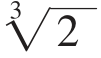 a,即为所求的倍立方的棱长。
a,即为所求的倍立方的棱长。