三角形到底有多少“心”?
三角形是由三条线段顺次首尾相连,组成的一个闭合的平面图形,它是边数最少的多边形,是平面图形中最基本也是最重要的图形,在生产和生活中有着十分广泛的应用。
一个简单的三角形,却蕴含着无数丰富且奇妙的性质。下面我们就谈谈三角形的一些基本性质和三角形的“五心”“费马点”、九点圆及圆心的确定等。
一个三角形,一般用大写英语字母表示顶点,用小写英语字母表示边,用阿拉伯数字表示角,如图1所示。
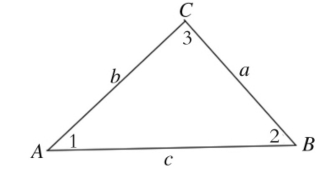
图1
各种各样的三角形,如图2所示。
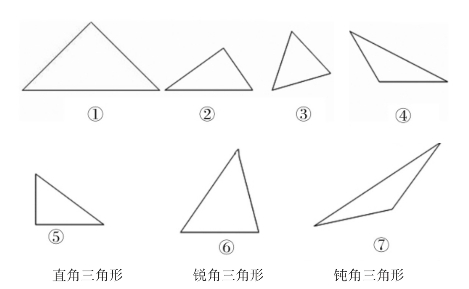
图2
1.三角形的分类
(1)按角度分:
a.锐角三角形:三个角都小于90度的三角形;
b.直角三角形:简称Rt△,其中有一个角等于90度;
c.钝角三角形:有一个角大于90度,但小于180度的三角形。
其中锐角三角形和钝角三角形统称为斜三角形。
(2)按边分:
a.不等边三角形:3条边互不相等的三角形;
b.等腰三角形:有2条边相等的三角形;
c.等边三角形:3条边都相等的三角形,也叫正三角形。
2.三角形的一些基本性质
(1)三角形三个内角的和等于180度;
(2)三角形的一个外角等于与它不相邻的两个内角的和;
(3)三角形的外角和是360°;
(4)三角形任何两边之和大于第三边;
(5)三角形任意两边之差小于第三边;
(6)等腰三角形的顶角平分线,底边的中线,底边的高重合,即三线合一;
(7)直角三角形的两个锐角互余(和为90度);
(8)直角三角形斜边的中线等于斜边的一半;
(9)三角形的任意一条中线将这个三角形分为两个面积相等的三角形;
(10)三角形具有稳定性,不易变形等。
3.三角形的基本定理
(1)中位线定理:三角形的中位线平行于第三边且等于第三边的一半。
(2)中线定理:三角形一条中线两侧所对边的平方和等于底边的平方的一半与该边中线平方的2倍的和;三角形三条中线的长度的平方和等于它的三边长度的平方和的3/4。
设△ABC的三边为:a,b,c,c边上的中线长为lc,则中线定理的数学表达式为:a2+b2=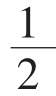 c2+
c2+
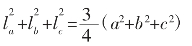
(3)勾股定理(毕达哥拉斯定理):在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方。
几何语言:若△ABC满足∠ABC=90°,则AB2+BC2=AC2。
(4)勾股定理的逆定理也成立,即两条边长的平方之和等于第三边长的平方,则这个三角形是直角三角形。
(5)射影定理:在任何一个直角三角形中,作出斜边上的高,则斜边上高的平方等于两直角边在斜边上的射影长的乘积。
几何语言:若△ABC满足∠ACB=90°,作CD⊥AB,则CD2=AD×BD。
(6)射影定理的拓展:如图3,若△ABC满足∠ACB=90°,作CD⊥AB,则
①AC2=AD·AB
②BC2=BD·AB
③AC×BC=AB×CD
(7)正弦定理:在任何一个三角形中,每个边与所对角的正弦之比都相等且等于三角形外接圆的直径。
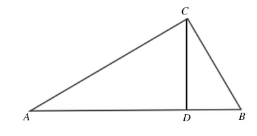
图3
几何语言:在△ABC中,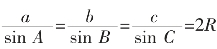 (R是外接圆半径)。
(R是外接圆半径)。
(8)结合三角形面积公式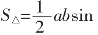 C,正弦定理可以变形为:
C,正弦定理可以变形为:

(9)设三角形的三条边长、外接圆的半径、面积分别为a、b、c、R、S△,
则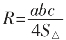
(10)余弦定理:在任何一个三角形中,任意一边的平方等于另外两边的平方和减去这两边的2倍乘以它们夹角的余弦。
几何语言:在△ABC中,a2=b2+c2-2bc×cos A;
此定理可以变形为:cos A=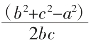 。
。
(11)梅涅劳斯定理:梅涅劳斯(Menelaus)定理是由古希腊数学家梅涅劳斯首先证明的。它指出:如果一条直线与△ABC的三边AB、BC、CA或其延长线交于F、D、E点,那么
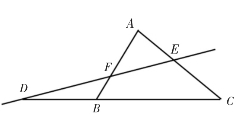
图4
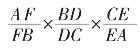 =1(如图4)
=1(如图4)
它的逆定理也成立:
若有三点F、D、E分别在的边AB、BC、CA或其延长线上,且满足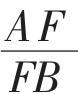 ×
×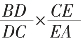 =1,则F、D、E三点共线。
=1,则F、D、E三点共线。
利用这个逆定理,可以判断三点共线。
(12)塞瓦定理:设O是△ABC内任意一点,AO、BO、CO分别交对边于D、E、F,则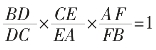 。
。
利用塞瓦定理的逆定理也可以证明三角形三条高线必交于一点。
4.三角形的“五心”
三角形的“五心”分别为:重心、外心、内心、垂心、旁心。
(1)三角形的重心
三角形的三条中线相交于一点,交点叫做三角形的重心(如图5)。
相关性质:
①重心到顶点的距离与重心到对边中点的距离之比为2∶1。设三角形重心为O,BC边中点为D,则有AO=2OD;
②在平面直角坐标系中,重心的坐标是顶点坐标的算术平均数。
设三角形三个顶点的坐标分别为(x1,y1),(x2,y2),(x3,y3),
其重心坐标为:[(x1+x2+x3)/3,(y1+y2+y3)/3];
③三角形的重心与三顶点的连线所构成的三个三角形面积相等;
④三角形的重心也是它三边的中点所连成的三角形的重心;
⑤重心到三角形三个顶点的距离平方之和最小;
⑥以重心为起点,以三角形三顶点为终点的三条向量之和等于零向量。
(2)三角形的外心
三角形三边的垂直平分线相交于一点,交点称为三角形的外心(如图6)。
相关性质:
①外心到三角形三顶点的距离相等;
②过三角形各顶点的圆叫做三角形的外接圆,外接圆的圆心即三角形的外心,这个三角形叫做这个圆的内接三角形,三角形有且只有一个外接圆;

图5

图6
③当三角形为锐角三角形时,外心在三角形内部;当三角形为钝角三角形时,外心在三角形外部;当三角形为直角三角形时,外心在斜边上,与斜边的中点重合。
(3)三角形的内心
三角形三条内角平分线相交于一点,交点称为三角形内心(如图7)。
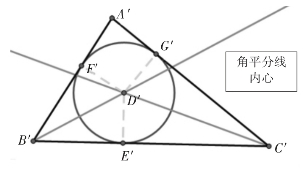
图7
相关性质:
①内心到三角形三边的距离相等;
②与三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心即是三角形内心,这个三角形叫做圆的外切三角形,三角形有且只有一个内切圆。
(4)三角形的垂心
三角形三边上的三条高或其延长线相交于一点,交点称为三角形的垂心(如图8)。
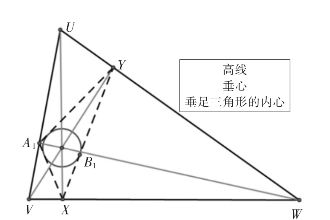
图8
相关性质:
①锐角三角形的垂心在三角形内;直角三角形的垂心在直角的顶点;钝角三角形的垂心在三角形外;
②三角形的垂心与三顶点这四点中,任一点是其余三点所构成的三角形的垂心;
③垂心关于三边的对称点,均在△ABC的外接圆上;
④锐角三角形的内接三角形(顶点在原三角形的边上)中,以垂足三角形的周长为最短;

图9
⑤三角形三个顶点,三个垂足,垂心这7个点可以得到6个四点共圆;
⑥垂心分每条高线的两部分乘积相等。
(5)三角形的旁心
三角形的一条内角平分线与其他两个角的外角平分线相交于一点,交点称为三角形的旁心(如图9)。
相关性质:
①与三角形的一边及其他两边的延长线都相切的圆叫做三角形的旁切圆,旁切圆的圆心就是三角形的旁心;
②旁心到三角形一边及其他两边延长线的距离相等;
③三角形有三个旁切圆,三个旁心。这三个旁心到三角形三条边或其延长线的距离都相等;
④直角三角形斜边上的旁切圆的半径等于三角形周长的一半。
(6)三角形的中心
只有正三角形才有中心,这时重心,内心,外心,垂心,四心合一。
(7)“五心”之间也有很多密切的联系,还有许多重要的性质:
①三角形的内心、旁心到三边的距离都相等;
②锐角三角形的垂心是它垂足三角形的内心;
③三角形的内心是它旁心三角形的垂心;
④三角形的外心是它的中点三角形的垂心;
⑤三角形的中点三角形的外心也是其垂足三角形的外心;
⑥三角形的任一顶点到垂心的距离,等于外心到对边的距离的二倍;
⑦锐角三角形的垂心到三顶点的距离之和等于其内切圆与外接圆半径之和的2倍;
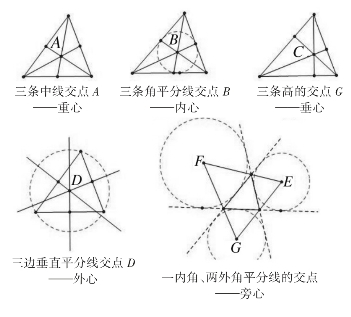
图10
⑧三角形一内角平分线与其外接圆的交点到另两顶点的距离与到内心的距离相等;
⑨(欧拉定理)在△ABC中,R和r分别为外接圆和内切圆的半径,O和I分别为其外心和内心,则OI2=R2-2Rr;
⑩三角形外心O、重心G和垂心H三点共线,且OG﹕GH=1﹕2。(此直线称为三角形的欧拉线,或三角形的外心、重心、九点圆圆心、垂心,依次位于同一直线上,这条直线也叫三角形的欧拉线。
5.三角形的费马点(等角中心)
费马是17世纪法国的一位律师和政府的公务员,但却是一位数学天才。他利用闲暇的时间研究数学,取得了非凡的成就,被称为业余数学之王,他几乎与同时代的所有欧洲的大数学家保持着通信联系。在当时,费马就是欧洲所有数学研究进展的交换中心。
有一天,他要回答一个收到的问题,“要找出三角形里最小点的位置,这个最小点是指这点到三个顶点的距离总和为最短”。也就是说,“在平面上找一个点,使此点到已知三角形三个顶点的距离之和为最小”,费马找到了这个点,这个点就是后来命名的“费马点”。这个问题有着非常实际的应用,例如有三个城市,然后要盖一个交通中心,希望到这三个城市的距离之和最短这一类的问题。
如图11,给定一个三角形△ABC,是否存在一点P到三角形的三个顶点A、B、C的距离之和比从其他点算起来的都要小,这个点就称为三角形的费马点。费马证明了这个特殊的点对于每个给定的三角形不但存在而且只有一个。
下面分两种情况来讨论费马点的确定。
(1)若三角形三个内角均小于120°,那么费马点到三顶点的距离连线正好三等分费马点所在的周角,即该点所对三角形三边的张角相等,即∠BPC=∠BPA=∠APC=120°。所以三角形的费马点也称为三角形的等角中心。
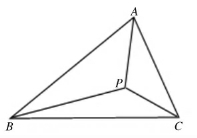
图11
(2)若三角形有一内角大于等于120°,则此钝角的顶点就是距离和最小的费马点。
如何用尺规作图法找到费马点呢?
只考虑三角形的三个内角均小于120°的情况。
方法一:
对于每一个角都小于120°的三角形ABC,以每一条边为底边,向外作正三角形,然后作这三个正三角形的外接圆。这三个外接圆会有一个共同的交点O,而这个交点O就是所要求的费马点(如图12)。
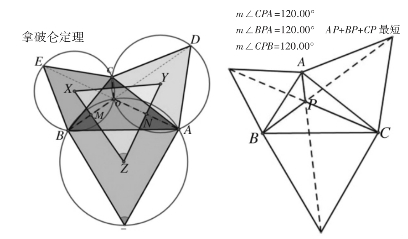
图12
在此方法中,三个等边三角形的中心X、Y、Z也构成等边三角形,据说是拿破仑发现的,故称为拿破仑三角形。
方法二:
①以三角形任意一边a向外作等边三角形BCD;
②找出该等边三角形的外心,并作出外接圆;
③连结a边所对的两个顶点(连接AD);
④该连线与外接圆的交点P即为该三角形的费马点。
证明一:如图13,P,B,D,C四点共圆,∠BDC=60°,所以∠BPC=180°-∠BDC=120°
又弧BD所对的圆周角∠BPD=∠BCD=60°,所以∠APB=120°
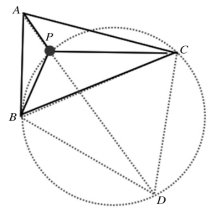
图13
所以,∠APC=120°
故点P就是所求的费马点。
证明二:在△ABC内任取一点P,如图14,向外作正△ABA′,
再作一正△PBP′,P′与C相对于BP,
容易看出,∠1=∠2,A′B=AB,P′B=PB,
则△APB≌△A′P′B,进而PA=P′A′。
即PA+PB+PC=P′A′+P′P+PC。
A′和C是定点,若要使距离和最小,则需要P′P在直线A′C上。
此时,∠3=180°-60°=120°,则∠4=∠3=120°,因此P、A、B、A′四点共圆。
同理可证其余各角都是120°。
这就是说,向△ABC外作正△ABA′,作其外接圆交A′C于P,P就是费马点。
而且,P到三角形三个顶点距离之和的最小值就是A′C。
方法三:
①以三角形的两边向外分别做等边三角形;
②连接两边相对的两个顶点;
③该连线的交点即为所求的费马点。
如图15,以△ABC的两边为底边向外作等边△ABD、△ACE,
连接CD、BE交于点O,O是费马点。
证明:在△ACD、△AEB中,
AD=AB
∠DAC=∠BAE
AC=AE
∴△ADC≌△ABE(SAS)
∴∠ADC=∠ABE
∴A、D、B、O四点共圆。
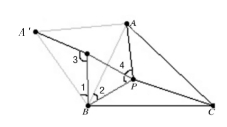
图14

图15
∴∠AOB=120°(对角互补)。
同理可得,∠AOC=120°
所以,∠AOB=∠AOC=∠BOC=120°
所以,点O是费马点。
那如何证明费马点到三角形三个顶点的距离之和最小呢?
如图16,已知在△ABC中,P是费马点,M为其三角形中任意一点。连接AM,BM,CM。
以点B为旋转中心,将BM逆时针旋转60°到BQ,得到正△BMQ
在△BMC与△BQA′中,
BM=BQ,BC=BA′,∠MBC=∠QBA′
所以,△MBC≌△QBA′(SAS)
所以,MC=QA′
因此,MA+MB+MC=AM+MQ+QA′
而,PA+PB+PC=AA′(前面已证)
所以MA+MB+MC>PA+PB+PC=AA′(两点之间的折线段大于直线段)
由此可知PA+PB+PC最小。
现在来看三角形三个内角中有一个大于或等于120°的情况。
证明:不妨假设在△ABC中有一个内角
∠BAC≥120°。
如图17所示,设P为△ABC内任一点,
将△APC绕A点逆时针旋转,使C转到BA的延长线上的C′点,P转到P′。
此时,AP=AP′,PC=P′C′,AC=AC′
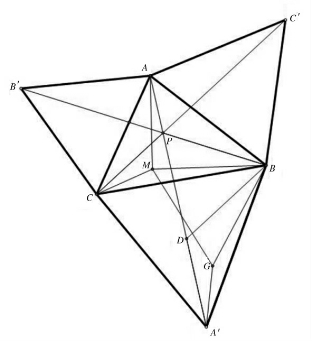
图16
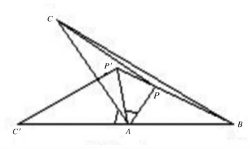
图17
由于旋转的角度为180°-∠BAC≤60°,所以∠AP′P≥60°
所以PP′≤AP。
于是PA+PB+PC≥BP+PP′+P′C′≥BC′=AB+AC
上式等号当且仅当P点与A点重合时成立。
这就是说,当∠BAC≥120°时,极值点P是顶点A,也就是费马点。
例1:已知正方形ABCD内一动点E到A、B、C三点的距离之和的最小值为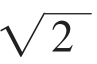 +
+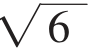 ,求此正方形的边长。
,求此正方形的边长。
分析:如图18,连接AC,发现点E到A、B、C三点的距离之和就是到△ABC三个顶点的距离之和,这实际上就是费马点问题的变形。
解:如图18,连接AC,点E就是△ABC的费马点,由于ABC是等腰直角三角形,故可知点E在正方形ABCD的对角线BD上。
以AC边为底边向外做等边三角形ACG,则B、E、O、D、G五点共线,所以BG就是费马距离,也就是说EA+EB+EC=BG=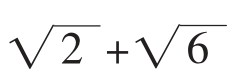 。
。
设正方形的边长为a,那么BO=OC=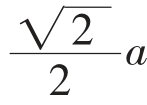 ,
,
所以OG=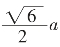 ,
,
所以,BG=BO+OG=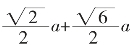
即,

图18
解得,a=2
故,所求正方形的边长为2。
三角形中这些特殊的“心”或“点”都有着广泛的实际应用。
如果有三个村庄A、B、C不在同一条直线上,村与村之间有直线公路相连。
①若取一点P打水井,使从水井P到三村庄A、B、C所铺设的输水管总长度最小,则此时满足条件的点P就是“费马点”;
②如果要求水井P到三村庄A、B、C的距离相等,此时满足条件的点P就是“外心”;
③如果取一点P建道路维修站,要求维修站到三条公路的距离都相等,此时满足条件的点P就是“内心”。
最后我们来看一个三角形中著名的九点共圆问题。
6.三角形的九点圆心
任意一个三角形三边的中点,三高的垂足和三个欧拉点(连结三角形各顶点与垂心所得三线段的中点),这九个点共圆。通常称这个圆为九点圆,或欧拉圆、费尔巴哈圆等(如图19)。
九点圆是几何学史上的一个著名问题,最早提出九点圆的是英国的培亚敏·俾几(Benjamin Beven),问题发表在1804年的一本英国杂志上。第一个完全证明此定理的是法国数学家彭赛列(1788—1867)。一位高中教师费尔巴哈(1800—1834)也曾研究了九点圆,他的证明发表在1822年的《直边三角形的一些特殊点的性质》一文里,文中费尔巴哈还获得了九点圆的一些重要性质,故有人称九点圆为费尔巴哈圆。
九点圆具有许多有趣的性质,例如:
①三角形的九点圆的半径是三角形的外接圆半径之半;
②九点圆的圆心在欧拉线上,且恰为垂心与外心连线的中点;
③三角形的九点圆与三角形的内切圆,三个旁切圆均相切(费尔巴哈定理);
④九点圆心(V),重心(G),垂心(H),外心(O)四点共线,且HG=2OG,OG=2VG,OH=2OV。
那如何证明九点共圆呢?
如图,设△ABC的BC边垂足为D,BC边中点为L,AC边垂足为E,AC边中点为M,AB边垂足为F,AB边中点为N,垂心为H,AH、BH、CH的中点分别为P,Q,R。只需证明所有的点都在以PL为直径的圆上,亦即证明其他的点与PL所张的角为90°,比如∠PEL=90°等。
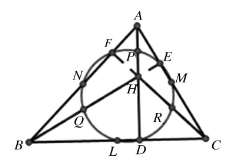
图19
证明:由于P、M分别是AH、AC的中点,所以中位线PM∥CH,
同理LM∥AB,又CH⊥AB,所以PM⊥LM,
又PD⊥LD,所以PMDL共圆。
同样由中位线知PR∥AC,LR∥BH,BH⊥AC,所以PR⊥LR
所以PMRDL五点共圆。
又因为,PE为直角△AHE斜边的中线,∠PEA=∠PAE,
同理∠LEC等于∠LCE,所以∠PEL=180°-∠PEA-∠LEC=90°,
所以,PEMRDL六点共圆;
同理以PL为直径,可知PFNQL五点共圆,进而可知PEMRDLQNF九点共圆。
由于九点圆以PL为直径,所以PL的中点(设为V)就是圆心。
总之,三角形虽然是平面几何中最简单、最基本的图形,也是实际生活中最常用的图形,但是三角形中却蕴藏着数不清的奥秘与规律,就是高科技飞速发展的现在,也许还有很多我们还不知道的规律与奥秘在等待人们去进一步发现。


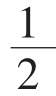 c
c



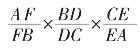 =1(如图4)
=1(如图4)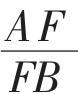 ×
×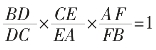 。
。












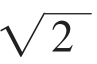 +
+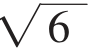 ,求此正方形的边长。
,求此正方形的边长。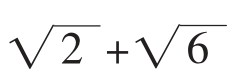 。
。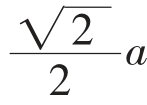 ,
,
