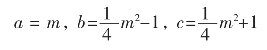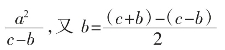千古第一定理——勾股定理
三角形是平面几何中最简单的直边封闭图形,也是应用最为广泛的基本几何图形。而直角三角形又是三角形中一类非常重要的特殊三角形,其直角三角形的性质也是数学家们研究的重点,特别是反映三边关系的勾股定理就是其中一个极为重要的定理。德国天文学家、物理学家、数学家约翰尼斯·开普勒曾说过,“几何学有两大珍宝,一个是毕达哥拉斯定理(也就是勾股定理),另一个是黄金分割,前者我们可比之为黄金,后者我们可称之为宝石”。因此,勾股定理也号称千古第一定理。
勾股定理的基本内容是:直角三角形两直角边(即“勾”“股”)边长的平方和等于斜边(即“弦”)边长的平方。
用数学符号语言叙述就是:
勾股定理:设直角三角形两直角边的长分别为a和b,斜边长为c,
那么a2+b2=c2。
勾股定理是人类早期发现并证明的重要数学定理之一,是用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一。世界上各文明古国都对勾股定理的发现和研究作出过重要贡献。
我国古代对这个定理的发现、应用和研究也具有自己明显的特色,如“勾三、股四、弦五”就是我国古代研究勾股定理的一个最著名的例子。
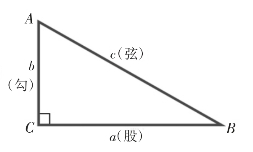
图1
大约在公元前十一世纪,周朝数学家商高就给出了“勾三、股四、弦五”这样一个特殊的直角三角形。事情是这样的,在中国古代早期的经典《周髀算经》中,就记录着商高同周公的一段对话。在研究测量问题时,商高对周公说:“……故折矩以为勾广三,股修四,经隅五”。这句话的意思为:当直角三角形的两条直角边分别为3(勾)和4(股)时,径隅(弦)则为5。这是一个最基本的直角三角形,也是古人确定直角的一种方法,认为边长为3、4、5的三角形一定是直角三角形。所以,以后人们就简单地把这个事实说成“勾三、股四、弦五”。根据该典故,此定理在中国就被称为“勾股定理”或商高定理。
公元三世纪,三国时代吴国的数学家赵爽,曾经对《周髀算经》内的勾股定理作出了详细注释,记录于《九章算术》之中。《九章算术》也是我国古代一部重要的数学著作,书中专设“勾股章”,正式提出了勾股定理,书中说:“勾股各自乘,并而开方除之,即弦”。即:
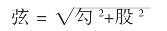
中国古代的数学家们不仅很早就发现并应用勾股定理,而且很早就尝试对勾股定理作理论的证明。最早对勾股定理进行证明的,就是数学家赵爽。赵爽创制了一幅“勾股圆方图”,用形数结合得到方法,给出了勾股定理的详细证明。
在这幅“勾股圆方图”中,以弦为边长得到的正方形是由4个相等的直角三角形再加上中间的小正方形组成的。
由图2可以看出,大正方形面积等于四个全等的直角三角形面积与小正方形面积的和。即
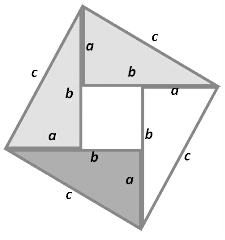
图2
整理得:a2+b2=c2
赵爽的这个证明极富创新意识。他用几何图形的截、割、拼、补来证明代数式之间的恒等关系,既具严密性,又具直观性,为中国古代以形证数、形数统一、代数和几何紧密结合、互不可分的独特风格树立了一个典范。以后的数学家大多继承了这一风格并且代有发展。
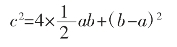
与赵爽同时代的三国数学家刘徽,在注《九章算术》中亦证明了勾股定理。刘徽在证明勾股定理时,也是用的以形证数的方法,只是具体图形的分合移补略有不同而已。
刘徽是公元三世纪世界上最杰出的数学家,他在公元263年撰写的著作《九章算术注》以及后来的《海岛算经》,都是我国最宝贵的数学遗产,从而奠定了他在中国数学史上的不朽地位。
数学家刘徽证明勾股定理用的是“以盈补虚,出入相补”的“割补术”,其方法富有东方智慧,特色鲜明、通俗易懂。
刘徽描述此图时说,“勾自乘为朱方,股自乘为青方,令出入相补,各从其类,因就其余不动也,合成弦方之幂。开方除之,即弦也”。其大意为,一个任意直角三角形,以勾宽作红色正方形即朱方,以股长作青色正方形即青方。将朱方、青方两个正方形对齐底边排列,再进行割补——以盈补虚,分割线内不动,线外则“各从其类”,以合成弦的正方形即弦方,弦方开方即为弦长。所构造的图被称为“青朱出入图”,也很好地解决了勾股定理的证明。如图3:
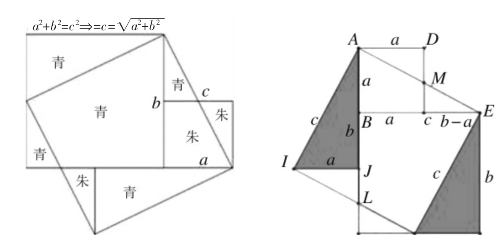
图3
中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位。尤其是其中体现出来的“形数统一”的思想方法,更具有科学创新的重大意义。事实上,“形数统一”的思想方法正是数学发展的一个极其重要的条件。正如当代中国数学家吴文俊所说:“在中国的传统数学中,数量关系与空间形式往往是形影不离地并肩发展着的。”
当然,勾股定理在古世界文明中也有着特殊的魅力。远在公元前约三千年的古巴比伦人就知道和应用勾股定理,他们还知道许多勾股数组。古埃及人在建筑宏伟的金字塔和尼罗河泛滥后测量土地时,也应用过勾股定理。
在西方,最早提出并证明此定理的,为公元前6世纪的古希腊数学家毕达哥拉斯,他用演绎法证明了直角三角形斜边平方等于两直角边平方之和,因而西方人都习惯地称这个定理为“毕达哥拉斯定理”。为了庆祝这一定理的发现与证明,毕达哥拉斯学派杀了一百头牛酬谢供奉神灵,以示庆贺,因此这个定理又有人叫做“百牛定理”。
毕达哥拉斯(Pythagoras,约公元前580年—约前500(490)年)古希腊数学家、哲学家。出生在爱琴海中的萨摩斯岛(今希腊东部小岛)的贵族家庭,自幼聪明好学,曾在名师门下学习几何学、自然科学和哲学。因为向往东方的智慧,经过万水千山,游历了当时世界上两个文化水准极高的文明古国——巴比伦和印度,吸收了阿拉伯文明和印度文明的文化。后来他就到意大利的南部传授数学及宣传他的哲学思想,并和他的信徒们组成了一个所谓“毕达哥拉斯学派”的政治和宗教团体。毕达哥拉斯对数学和哲学的贡献巨大,认为“万物皆数”,“数是万物的本质”,对数论、几何作出了突出的贡献,发现了自然数的很多性质,还发现了黄金分割和勾股定理,他还坚持数学论证必须从“假设”出发,开创了演绎逻辑思想,对数学发展影响很大。

毕达哥拉斯像
据说,毕达哥拉斯发现勾股定理还有一个有趣的故事。一天,毕达哥拉斯应邀参加一位富有政要的餐会,这位主人豪华宫殿般的餐厅铺的是美丽的正方形大理石地砖,由于大餐迟迟不上桌,这些饥肠辘辘的贵宾颇有怨言,但这位善于观察和理解的数学家却凝视着脚下这些排列规则、美丽的方形瓷砖。但毕达哥拉斯不只是欣赏瓷砖的美丽,而是想到它们和“数”之间的关系,于是拿了画笔并且蹲在地板上,选了一块瓷砖以它的对角线为边画了一个正方形,他发现这个正方形面积恰好等于两块瓷砖的面积和(如图4)。他很好奇,于是再以两块瓷砖拼成的矩形之对角线作另一个正方形,他发现这个正方形之面积等于5块瓷砖的面积,也就是以两股为边作正方形的面积之和。至此毕达哥拉斯作了大胆的假设:
任何直角三角形,其斜边的平方恰好等于另两边平方之和。
那一顿饭,这位古希腊数学大师,视线都一直没有离开过地面。从此,毕达哥拉斯定理闻名于世。
在古希腊,勾股定理最典型的证法是古希腊数学家欧几里得在《几何原本》中给出的证法,这个证明是平面几何中的经典内容,两千多年来多次被收入世界各国的教科书,至今都经久不衰。欧几里得给出的证法是:
如图5所示,以直角三角形ABC的三边AB,BC,CA,分别向外作正方形ABED,BCGK,ACHF,连接FB、CD,过点C作CL⊥DE交AB于M,交DE于L。
由图可以看出,
△FAB≌△CAD(边角边)。
△FAB的面积等于△CAD的面积等于矩形ADLM的面积的一半(同底等高),所以,矩形ADLM的面积=b2。
同理,矩形BELM的面积=a2,而正方形ADEB的面积=c2,所以,c2=a2+b2。
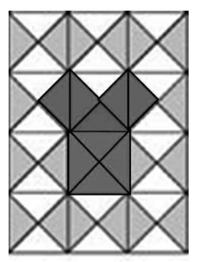
图4
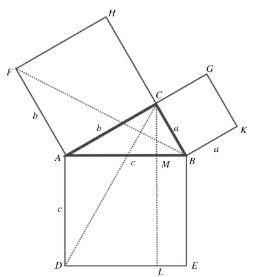
图5
根据欧几里得证明勾股定理时所画的图形,反复操作此画法,画出来的图形很像一棵大树,这棵树据说是由毕达哥拉斯根据勾股定理所画出来的一个可以无限重复的图形(如图6)。又因为重复数次后的形状好似一棵树,所以被称为毕达哥拉斯树。由直角三角形两个直角边平方的和等于斜边的平方,可得两个相邻的小正方形面积的和等于相邻的一个大正方形的面积。
据不完全统计,勾股定理现发现有400余种证明方法,是数学定理中证明方法最多的定理之一。
下面再给出几种较典型的证明思路。
证明思路一(据说是毕达哥拉斯给出的证明):
用全等的四个直角三角形拼成下列两种图形。从图上可以看出,两个正方形的边长均为a+b,所以面积相等,即
2ab+a2+b2=4× ab+c2
ab+c2
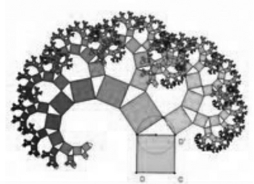
图6
整理得:a2+b2=c2
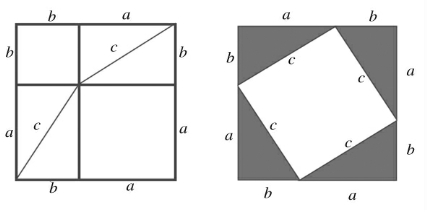
图7
证明思路二(构造法证明或邹元治证法):
由图8可以看出,大正方形面积等于四个全等的直角三角形面积与小正方形面积的和。即
(a+b)2=4×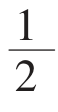 ab+c2
ab+c2
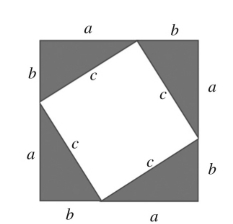
图8
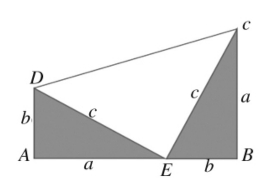
图9
整理得:a2+b2=c2
证明思路三(1876年第20届美国总统加菲尔德证法):
把两个全等的直角三角形拼成如图9的一个直角梯形,其中A、E、B在一条直线上,则由梯形的面积公式和三个直角三角形的面积和得到:
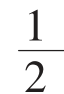 (b+a)(a+b)=2×
(b+a)(a+b)=2×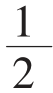 ab+
ab+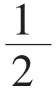 c2
c2
整理得:c2=a2+b2
证明思路四(迈克尔·哈代证法):
利用圆内接直角三角形,根据相似三角形对应边成比例得(如图10):
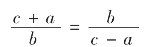

图10
整理得:a2+b2=c2
证明思路五(巧用射影定理证明):
如图11,在直角三角形ABC中,过C作CD垂直AB于D,则
△CAD∽△BAC
所以,AC2=AD×AB

图11
又△CBD∽△ABC
所以,CB2=BD×BA
所以,AC2+CB2=AD×AB+BD×BA=AB(AD+BD)=AB2,
即c2=a2+b2
“勾股数”:勾股定理也可以看作是三元二次不定方程,而且当整数a,b,c满足a2+b2=c2这个条件时,(a,b,c)叫做勾股数组。
常见的勾股数组有(3,4,5)(5,12,13)(6,8,10)(7,24,25)等。
如果(a,b,c)是一组勾股数,则对于任意正整数k,(ka,kb,kc)也是一组勾股数,这说明勾股数有无穷多组。
如何求勾股数,勾股数有没有一个表达式?答案是肯定的。
对于任意一组勾股数(a,b,c),可以表示的形式有:
(1)毕达哥拉斯表达式:
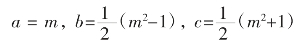
其中,m为奇数。
(2)柏拉图表达式:
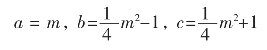
(3)丢番图表达式:
若m,n是两个正整数,且2mn是完全平方数,则有
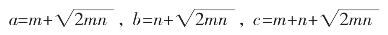
(4)刘徽表达式:

其中m,n均为正整数,且m>n。
显然,勾股数不定方程有无数多组正整数解。
(5)印度数学家也给出了勾股数的统一表达式
a=2mn,b=m2-n2,c=m2+n2
而且在勾股数中,必有一个是3的倍数,也必有一个是4的倍数,还有一个是5的倍数。因此,“勾三、股四、弦五”也就成了勾股定理的代名词。
勾股定理的推广:
(1)余弦定理:在一般三角形ABC中,
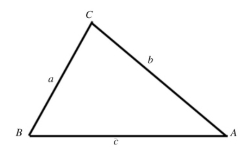
图12
a2=b2+c2-2bc cos A
b2=a2+c2-2ac cos B
c2=a2+b2-2ab cos C
当C为直角时,cos C=0,则c2=a2+b2。
所以,勾股定理是余弦定理中的一个特例。
(2)勾股定理也可推广到空间几何体,如在顶角均为直角的三棱锥P-ABC中,即∠APB=∠BPC=∠APC=90°。
可证得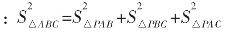
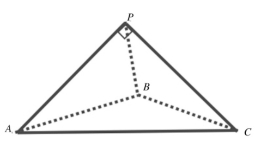
图13
(S△ABC表示三角形ABC的面积)
(3)费马大定理:不存在正整数x、y、z,使得当n>2(n是正整数)时,xn+yn=zn成立。
显然,只有当n=2时(n=1除外),方程xn+yn=zn才有正整数解,此时的解即为勾股数。
【勾股定理的逆定理】如果一个三角形ABC的三边a、b、c满足a2+b2=c2,那么三角形ABC为直角三角形。
勾股定理的用途:
(1)已知直角三角形任意两边长求解第三边;
(2)利用勾股定理可以求矩形的对角线长度;
(3)利用勾股定理可以求长方体的对角线长度;
(4)已知三角形的三边长度,可以判断该三角形是否为直角三角形;
(5)在实际问题中,利用勾股定理求线段长度、距离、高度等,这是勾股定理的最基本运用。
例1:如明朝数学家程大位在其《算法统宗》中有一道“戏放风筝”的题目:
三月清明节气,蒙童戏放风筝;
托量九十五尺绳,被风刮起空中;
量得上下相应,七十六尺无零;
纵横甚法问先生,算了多少为平?
答曰:五十七尺。
这是一个简单的勾股定理应用题。
题目的意思是:托量九十五尺绳,指绳长95尺,也就是斜边c;
量得上下相应,七十六尺无零,是指风筝的高度76尺,也就是b;
纵横甚法问先生,算了多少为平?是问风筝在地面上的投影到蒙童之间的距离a是多少尺?

图14
解:由勾股定理a2+b2=c2
得a2=c2-b2
所以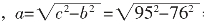 =57(尺)
=57(尺)
所以,风筝在地面上的投影到蒙童之间的距离是57尺。
例2:中国名典《九章算术》中记载了一道“葭生中央”的数学题:
今有池一方,葭生其中央,出水刚一尺。引葭赴岸,适与岸齐。问水深、葭长各几何(如图15)?
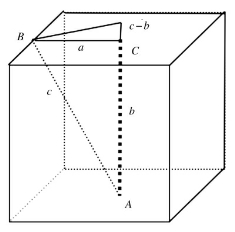
图15
答曰:水深一丈二尺;葭长一丈三尺。
葭是指初生的芦苇。现有一个一丈见方的池塘,芦苇生在其中央,露出水面刚一尺,把芦苇引到池边,芦苇的顶端刚好与水面持平。问水深、芦苇长各是多少?
术曰:半尺方自乘,以出水一尺自乘,减之,余,倍出水除之,既得水深,加出水数,得葭长。
分析:设半尺方是a,水深是b,葭长为弦c,则古人的算法就是下面的公式:
即: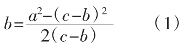
对于(1),由勾股定理可知
a2=c2-b2=(c-b)(c+b)
c+b=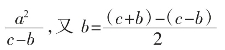
所以,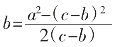
把a=5,c-b=1代入上式得
b=12(尺),c=13(尺)
勾股定理的历史意义:
(1)勾股定理是证明方法最多的一个定理,据公开发表的证明方法有近四百余种;
(2)勾股定理是历史上第一个把数与形联系起来的定理,即它是第一个把几何与代数联系起来的定理,没有勾股定理,就不可能有平面上两点间的距离公式;
(3)勾股定理导致了无理数的发现,引起了第一次数学危机,大大加深了人们对数的理解,促进了数系的发展;
(4)勾股定理是历史上第一个给出了完全解答的不定方程,由它引出了费马大定理等各式各样的不定方程的研究;
(5)勾股定理是欧氏几何的基础定理,并有巨大的实用价值。这条定理不仅在几何学中是一颗光彩夺目的明珠,被誉为“几何学的基石”,而且在高等数学和其他科学领域也有着广泛的应用;
(6)1971年5月15日,尼加拉瓜发行了一套题为“改变世界面貌的十个数学公式”邮票,这十个数学公式由著名数学家选出的,勾股定理是其中之首。






 ab+c
ab+c

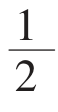 ab+c
ab+c

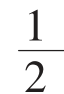 (b+a)(a+b)=2×
(b+a)(a+b)=2×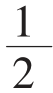 ab+
ab+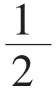 c
c