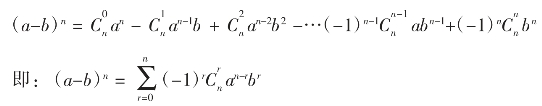杨辉三角形与二项式定理
运算能力是数学的三大能力之一,数学运算不但有数的运算,还有代数式的运算。如代数运算中的二项式(a+b)n(a、b不为零,n是自然数)的展开式,就是中学代数运算的重要内容之一。对二项式运算来说,随着指数n的不断增加,其二项展开式的规律也就成为人们研究的重要课题,而其中众多的规律也就被人们逐渐所熟知。我们来看下面的二项展开式:
(a+b)0=1
(a+b)1=a+b
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
(a+b)6=a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+b6
……
分析其右边的各项展开式可知:
(1)(a+b)n的展开式有n+1项;
(2)展开式中字母a的次数按降幂排列,从n,n-1,n-2,…一直到3,2,1,0。字母b按升幂排列,每一项的单项式次数均为n;
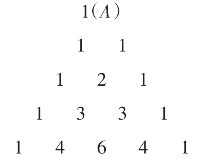
(3)展开式的系数规律排列如下:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
……
由此可以看出,二项式系数的排列类似于几何中的三角形。
上面数字排列最本质的特征是,它的两条腰边都是由数字1组成的,而其余的数则是等于它肩上的两个数之和。只要知道上一行展开式的系数,即可轻松得到下一行的展开式的系数,从而可以得到更多层的三角形。
这个规律最早由我国南宋数学家杨辉于1261年介绍面世的,后人称之为杨辉三角形。
杨辉,字谦光,南宋时期著名数学家。他在1261年所著的《详解九章算法》一书中,辑录了二项展开式的三角形数表,称之为“开方作法本源”图,后被称为杨辉三角形。这也是多项式(a+b)n打开括号后的各个项的二项式系数的规律。下面的图表就出自《详解九章算法》一书,这又是我国数学史上的一个伟大成就。
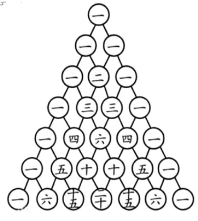
上表虽出自杨辉的《详解九章算法》,但杨辉却说明此表引自11世纪中叶(约公元1050年)贾宪的《释锁算术》,杨辉做了改进并绘画了“古法七乘方图”。故此,杨辉三角又被称为“贾宪三角”。在欧洲直到1623年以后,法国科学家帕斯卡才发现了这个三角形。帕斯卡在1655年的著作中介绍了几个关于此三角形的结果,并以此解决一些概率论上的问题,影响面广泛,所以欧洲一些科学家都用帕斯卡来称呼这个三角形,把这个表叫做“帕斯卡三角形”。这比杨辉要迟393年,比贾宪迟600年。中国古代数学家在数学的许多重要领域中都处于世界遥遥领先的地位,而杨辉三角的发现就是十分精彩的一页。进入20世纪以来,国外也逐渐承认这项成果属于中国,所以有些书上称这是“中国三角形”。
杨辉三角形有很多独特的性质:
(1)第一行1个数,第二行2个数,第三行3个数,……第n行n个数;
(2)每一行的第一个数和最后一个数均为1。其他的数都等于其肩上两个数(也就是上一行相邻的两个数)的和。如第五行中5=1+4,10=4+6等;
(3)每一行的数均具有对称性,开始时从小到大,中间有一个或两个数最大,然后由大到小。与第一项和最后一项等距离的两个数均相等;
(4)每一行的数字之和均是2的n次方,第n行的和即为2n;
1=20
1+1=21
1+2+1=22
1+3+3+1=23
1+4+6+4+1=24
1+5+10+10+5+1=25
1+6+15+20+15+6+1=26
……
(5)每一行(除去第一行)差、和相间的计算结果都是0;
1-1=0
1-2+1=0
1-3+3-1=0
1-4+6-4+1=0
1-5+10-10+5-1=0
1-6+15-20+15-6+1=0
……
(6)将杨辉三角左对齐,成如图所示排列,将同一斜行的数加起来。
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
即得斐波那契数列:1,1,2,3,5,8,13,…
可见,杨辉三角形与斐波那契数列也有着特殊的联系。由此让我们感受到了杨辉三角形蕴含着的无穷奥秘。当然,也还有很多奥秘需等你来发现。
我们来看一个有趣的例子。
假如我们在一个城里散步或开车兜风,假定这个城市是由一些方方正正的街区组成的,其中有一半的街道是从西北通向东南,而另一半的街道是由东北通向西南,两者十字交叉路口均畅通。当你沿着如图所示的那条锯齿状道路向前走时,从开始的A到末尾的P,经过了十个街区,在这个街道网络里,当然还有一些别的、也有十个街区那么长的、介于这两个端点之间的道路,但是比它更短的道路是不会有的。
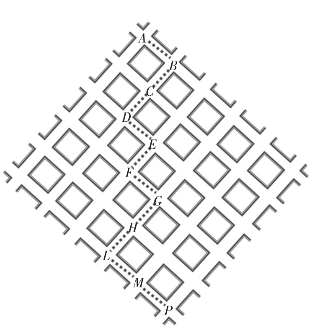
请问,在网络道路里找出从开始的A到末尾的P两点之间的不同的最短道路的数目。
归纳法是数学思维的一种重要方法,它引导我们由特殊情况去寻找一般的规律。我们先从最近的点开始数一数不同的走法数目。如从开始的A到B,只经过一条街道,显然只有1种方法;接下来从A到C,需要经过两条街道,显然有2种方法(既可以从A的左边走,也可以从A的右边走);再接下来从A到D,需要经过三条街道,数一数有3种方法。如此进行下去,如果我们标上从最开始的A到达每一个格点的走法数目,我们就得到了如下一列数表。
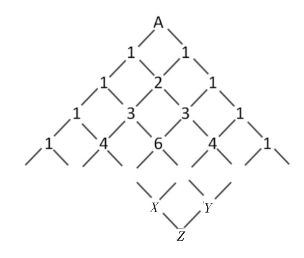
很显然这就是杨辉三角形。其实,道理很简单,在网络道路里,考虑三个街角,点X,Y和Z,他们的互相位置如图所示。在我们选择的最短道路从A到达Z,就必须经过X,或者经过Y,一旦到了X,再进一步到Z也只有一条路,到Y也一样,所以从A到Z最短道路的总数是两部分的和,也就是从A到X的道路数目加上从A到Y的道路数目。这就是我们观察到的结果,也是这个问题的一般规律。由此扩展杨辉三角形,选择我们需要的菱形区域,就可以得到最下面的P所对应的数目是252,也就是从最开始的A到最末尾的P共有252种最短道路数目。

这也是杨辉三角形的一个基本应用。
显然,有了杨辉三角形,我们对于次数不高的二项展开式,就能很方便的写出其结果。尤其是项数或次数在10以内的运算,就比较方便。若次数较高(比如20次,30次,任意n次等),或者要研究展开式的其中某几项等,只用杨辉三角形是远远不够的。因此,人们还得寻找更一般的规律,这也就是我们现在所看到的二项式定理。
二项式定理(Binomial theorem),又称牛顿二项式定理,由英国伟大的数学家、物理学家、天文学家和自然哲学家艾萨克·牛顿于1664年、1665年间提出,该定理给出了两个数之和的整数次幂展开项之和的一般恒等式。
二项式定理可以用以下公式表示:
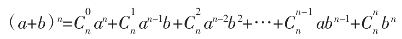
即:(a+b)n=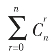 an-rbr,其中
an-rbr,其中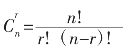
(n!=n(n-1)(n-2)…3×2×1)
其中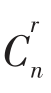 称为二项式系数,也是一个组合数。
称为二项式系数,也是一个组合数。
二项式定理的一些相关性质:
(1)(a+b)n展开式的项数共有n+1项;
(2)展开式的每一项a与b的指数之和为n,即二项展开式各项的次数等于二项式的次数n,字母a的指数依次降幂排列,指数由n逐次减1直到0,字母b按升幂排列,指数从0起逐项加1到n;
(3)其任意一项均可用公式表示为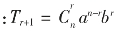 ;距首末两项等距离的二项式系数相等,即
;距首末两项等距离的二项式系数相等,即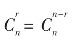 ;
;
(4)二项式系数的中间一项或中间两项的二项式系数最大:当n为偶数时,中间一项的二项式系数最大;当n为奇数时,中间两项的二项式系数相等且最大;
(5)在二项展开式中各项的二项式系数和为2n,
即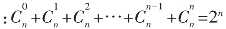 ,(在定理中只需令a=1,b=1即可);
,(在定理中只需令a=1,b=1即可);
(6)在二项展开式中,奇数项二项式系数的和等于偶数项二项式系数的和,都等于2n-1,即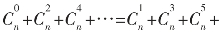 …=2n-1(令a=1,b=-1)。
…=2n-1(令a=1,b=-1)。
同样我们还可以得到:
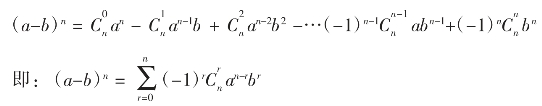
例:展开(x+1)10,则
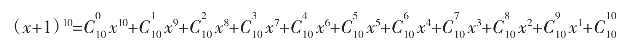
=x10+10x9+45x8+120x7+210x6+252x5+210x4+120x3+45x2+10x+1
在上式中,令x=1,则得到:
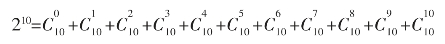
=1+10+45+120+210+252++210+120+45+10+1
二项式定理与杨辉三角形是一对天然的数形趣遇,它把数形结合带进了计算数学。求二项式展开式系数的问题,实际上是一种组合数的计算问题。用系数通项公式来计算,称为“式算”,用杨辉三角形来计算,称作“图算”。
牛顿还把二项式定理推广到任意的实数次幂,即广义的二项式定理,这些将在高等数学里可以学到。
下面,我们把杨辉三角形做一个推广,来看一下所谓的三项式系数表。
0 1 0
0 1 1 1 0
0 1 2 3 2 1 0
0 1 3 6 7 6 3 1 0
0 1 4 10 16 19 16 10 4 1 0
0 1 5 15 30 45 51 45 30 15 5 1 0
……
首先,我们来看看这张表是怎么构成的。
上表中,每一行的数都是三项式(1+x+x2)n的展开式中x方幂的系数。这也就是三项式系数名称的由来。看看下面的算式:
(1+x+x2)0=1
(1+x+x2)1=1+x+x2
(1+x+x2)2=1+2x+3x2+2x3+x4
(1+x+x2)3=1+3x+6x2+7x3+6x4+3x5+x6
(1+x+x2)4=1+4x+10x2+16x3+19x4+16x5+10x6+4x7+x8
……
再看三项式系数表都有那些性质:
(1)每一行都以0,1开始,以1,0结束;
(2)第n行里有2n+1个数,关于中间数左右对称,整个表也是中轴对称;
(3)每行除0,1和1,0外,每一个数都等于上一行上的三个数——西北、正北和东北三个相邻的和,例如,16=3+6+7,45=10+16+19;
(4)每行的系数和是3的方次幂;
1=30
1+1+1=31
1+2+3+2+1=32
1+3+6+7+6+3+1=33
1+4+10+16+19+16+10+4+1=34
1+5+15+30+45+51+45+30+15+5+1=35
……
(5)每行系数的差、和相间求和是定值1。
1=1
1-1+1=1
1-2+3-2+1=1
1-3+6-7+6-3+1=1
1-4+10-16+19-16+10-4+1=1
1-5+15-30+45-51+45-30+15-5+1=1
……
当然,此表中还有很多有趣的性质,如每行的系数的平方与三项式系数的关系,此表与杨辉三角形的关系等,读者有兴趣也可做深入研究。
最后,我们再来看一个应用的例子。
有一年,中国科技大学在一次招收少年班的测试中,给出了这样一道题目:
“今天是星期天,再过10的100次方天是星期几?”
此题形式简单,思路清楚,主要考查学生的变通能力、归纳能力和求简能力。若直接运算,计算量还是较大的,因此也难倒了不少学生。但也有不少同学给出了奇妙的解法,现摘录几例与大家分享:
方法一:由于星期的周期是7天,要解决此问题,也就是要求10100除以7的余数问题。有同学就想到了二项式定理,利用二项式定理解决求余数问题简单快捷。
因少年班招收的多是高中没毕业的学生,多数学生还没有学过二项式定理(此内容是高二的数学内容),只有少数同学自学过二项式定理或看过相关的内容,才有可能用此方法解决。
其解决思路是:
10100=(7+3)100
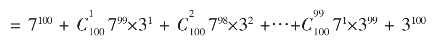
由此可以看出,展开式中除最后一项外,其余的各项均能被7整除。因而问题等价为求3100除以7的余数,而3100=950=(7+2)50;
以此类推,只需求250除以7的余数,而250=3210=(4×7+4)10;
继续求410除以7的余数。因410=165=(2×7+2)5;
只需求25除以7的余数即可,故所求余数为4。
所以10100除以7的余数为4,由于星期的周期是7,所以再过10100天与再过4天等价,因此最后答案是星期四。
方法二:也有同学选用归纳的方法,寻找10n除以7的余数的变化规律,最终获得答案。
解答如下:
10的1次方除以7,余数是—3;
10的2次方除以7,余数是—2;
10的3次方除以7,余数是—6;
10的4次方除以7,余数是—4;
10的5次方除以7,余数是—5;
10的6次方除以7,余数是—1;
10的7次方除以7,余数是—3;
10的8次方除以7,余数是—2;
……
由此看出,10的n次方除以7的余数是一个循环过程,余数依次为3-2-6-4-5-1,6个数一循环,不断往复。因为
100÷6=16……4
也就是10的100次方与10的4次方同余,10的4次方除以7余4,故10的100次方除以7也余4。
所以,再过10的100次方天是星期四。
方法三:也有同学试图用普通除法计算,如果能坚持算下去,也会找到循环规律。10的100次方,即为1后面连续有100个0,除以7的算式如下:
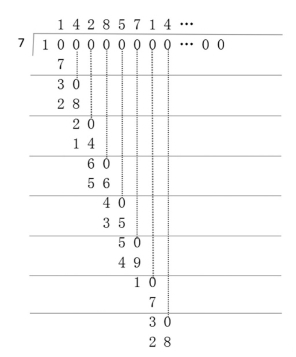
由此可以看出,商的结果是14285714285714…,商也是每6个数一循环,因为10的100次方是1后面有100个0,所以,100÷6=16…4。
也就是排除前面反复循环的,后面还有4个0,因此只需求10000除以7的余数即可,由上式可知余数是4。
所以,再过10的100次方天是星期四。
【小资料】
中国科学技术大学少年班
1978年3月9日,在著名物理学家、诺贝尔物理奖获得者李政道先生的大力倡导和热心支持下,在邓小平、方毅等国家领导人的支持和推动下,中国科学技术大学创建了少年班,主要招收尚未完成常规中学教育,但成绩优异的青少年接受大学教育。成立少年班的目的就是探索中国优秀人才培养的规律,培养在科学技术等领域出类拔萃的优秀人才,推动中国科技、教育和经济建设事业的发展。在2008年中国科学技术大学少年班创办30周年之际,中国科学技术大学将原少年班管委会(系级建制)升格为少年班学院。自少年班创立以来,中国科学技术大学不断探索和改善教学管理模式,倾力保证少年班教学和管理的开展。三十多年的经验积累,凝练成了“因材施教”“教学相长”“基础与创新并重”的办学理念和重基础、“轻”专业的宽口径个性化培养模式。秉承中国科大的办学理念,目标定位为培养未来10~20年后中国乃至世界上学术界、产业界科技创新的领军人物。
中国科学技术大学少年班创办30多年来,根据智力早慧少年的特点,探索了一条通识教育和因材施教相结合、专业教育与全面素质教育协调发展的培养模式,培养出一批最年轻的国内外著名学术机构的博士、教授,初步实现了少年班早出人才、出高质量人才的办学目标。通过对少年班毕业生追踪调查情况,统计数据表明:少年班毕业生中,考取研究生的占91%,64%获得博士学位。据不完全统计,他们中约20%选择学术研究作为自己的终身职业,许多人已成为国际著名科学家。有超过70%的少年班毕业生活跃在海内外经济、IT、金融、制造等领域,其中在世界500强企业任职的约35%。在国际学术前沿,少年班毕业生同样取得突出成绩,已知有多人在西方一流研究型大学任正教授,有多人当选IEEE(电气与电子工程师协会)会员,多人当选美国物理学会会员,另有数人入选美国医疗信息科学院、美国光学学会等会员,有多人获得海外华人物理学会优秀青年科学家奖,新加坡李光耀顶尖科研奖,美国Sloan研究奖,青年科学家总统奖,杰出青年电子工程师奖,国家自然基金成就奖,材料学会青年科学家奖,Parkard科学和工程奖等国际知名大奖。在北大、清华、中国科大、复旦等一流名校担任教授的就有20余人。





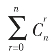 a
a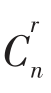 称为二项式系数,也是一个组合数。
称为二项式系数,也是一个组合数。