最大与最小,最远与最近
高斯说:“数学是科学之王”,一切科学研究与生活实践都离不开数学,尤其是当今世界随着科技的高速发展,大数据时代的来临,数学已经成为现代人最基本的素养,不懂数学就如文盲一样可怕。所以学习数学不只是一种计算、一种形式、一种逻辑游戏,更多的是科技实用、工作必用、生活有用。
在应用数学知识解决日常生活中的一些实际问题时,经常会出现解决方案不止一种,有时还会有无数种的情况。在这种情况下,我们往往需要找到最优的解决方案,如最大与最小、最远与最近等。下面分类举一些实例。
问题一:现有长度为1米的隔离护栏30个,在公园内围成一个矩形花坛,要使围成的面积最大,则长和宽应各是多少米?
分析:由于每个护栏的长度都是1米,所以围成的矩形长和宽必须都是整数(自然数),且长和宽这两个整数的和必是15。
问题转化为:两个整数的和是15,要使两个整数的乘积最大,这两个整数各是多少?
将两个整数的和为15的所有情况都列出来,考虑到加法与乘法都符合交换律,所以共有下面7种情况:
15=1+14,1×14=14;15=2+13,2×13=26;15=3+12,3×12=36;15=4+11,4×11=44;15=5+10,5×10=50;15=6+9,6×9=54;15=7+8,7×8=56。
由此可知把15分成7与8之和,则这两数的乘积最大。
也就是围成的矩形花坛长是8米(8个护栏),宽是7米(7个护栏),面积最大,最大面积是56平方米。
由此可得到如下的结论:
“如果两个整数的和一定,那么这两个整数的差越小,他们的乘积越大。特别地,当这两个数相等时(如果可以相等),他们的乘积最大。”
例如两个数的和是16,那么分成的两个数均为8时其乘积最大,即8×8=64。而其他的乘积如:7×9=63,6×10=60,5×11=55等,显然都比64要小。
变式一:如果在上述问题中,周长是30米的护栏可以任意弯折,则围成的矩形长和宽都是7.5米时,即围成的矩形是正方形时,面积最大,最大面积是:7.5×7.5=56.25(平方米)
所以,周长一定的长方形中,以正方形面积为最大。
证明如下:
设a+b=s(s是定值),由均值不等式,可知,
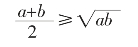
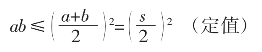
当且仅当a=b时,ab取得最大值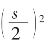 。
。
变式二:如果上述问题的30个护栏围成一个正六边形花坛,则其每边的长为5个护栏,即边长是5米,此时正六边形的面积是(如图1):
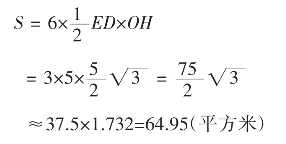
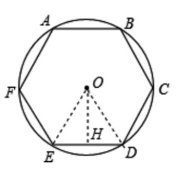
图1
显然,周长一定,正六边形的面积要比正方形的面积大一些。
变式三:如继续构造正多边形,如正十二边形,周长30米不变,此时正十二边形的面积是(如图2):
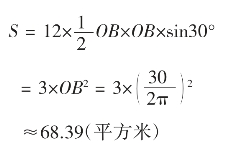
由此可知,周长一定时,正十二边形的面积大于正六边形的面积。所以,周长一定时,正多边形的边数越多面积越大。由极限的思想可知,当正多边形的边数无限增加时,正多边形的面积就趋于圆的面积。
此时圆的面积是:S=πR2=π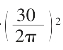 =71.62(平方米)
=71.62(平方米)
图2
有此,可得到结论:
周长一定时,所围成的图形中,以圆的面积为最大。
下面再看几个“最大”的例子。
例1:1~8这八个数字各用一次,分别写成两个四位数,使这两个数相乘的乘积最大,那么这两个四位数各是多少?
分析:高位数字越大,乘积越大,所以它们的千位分别是8,7,百位则分别是6,5。因为两数和一定时,这两个数越接近,乘积越大,所以一个数的前两位应是85,另一个数的前两位就是76。同理可确定十位数和个位数,则所求的两个四位数是8531和7642,它们的乘积是最大的。最大乘积为:
8531×7624=65040344
若是8624×7531=64947344,显然要小很多。
例2:把17分成几个自然数的和,怎样分才能使它们的乘积最大?
分析:假设分成的自然数中有1,a是分成的另一个自然数,因为1×a<1+a,也就是说,将1+a作为分成的一个自然数要比分成1和a两个自然数好,所以分成的自然数中不应该有1。如果分成的自然数中有大于4的数,那么将这个数分成两个最接近的整数,这两个数的乘积大于原来的自然数。例如,5=2+3<2×3,8=3+5<3×5。也就是说,只要有大于4的数,这个数就可以再分,所以分成的自然数中不应该有大于4的数。如果分成的自然数中有4,因为4=2+2=2×2,所以可以将4分成两个2。由上面的分析得到,分成的自然数中只有2和3两种。因为2+2+2=6,2×2×2=8,3+3=6,3×3=9,说明虽然三个2与两个3的和都是6,但两个3的乘积大于三个2的乘积,所以分成的自然数中最多有两个2,其余都是3。由此得到,将17分为五个3与一个2时乘积最大,最大值为:
3×3×3×3×3×2=486
结论:整数分拆的原则:不拆1,少拆2,多拆3。
例3:有一类自然数,各位上的数字从第三个数字开始,每个数字都恰好是它前面两个数字之和,直至不能再写为止,如358,1347等,这类数中最大的自然数是多少?
这个数应该是:10112358
分析:要想使自然数尽量大,数位就要尽量多,所以数位高的数值应尽量小,故最高位应取1,第二位也应尽量小,故可取0,因此最大的自然数应是10112358。如果最前面的两个数字越大,则按规则构造的数的位数较少,所以最前面两个数字尽可能地小,故取1与0即可。
例4:有一块边长为a的正方形铁皮,四个角各剪去一个相等的小正方形,围成一个无盖的正四棱柱盒子,怎样剪裁小正方形,才能使盒子容积最大?(如图3)
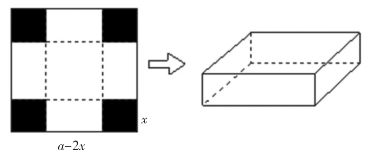
图3
分析:设剪去的小正方形边长为x,则做成的正四棱柱盒子的底部正方形边长为a-2x,令盒子的容积为V,则
V=(a-2x)2x
由均值不等式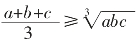 (当且仅当a=b=c时取“=”号)
(当且仅当a=b=c时取“=”号)
可知V=(a-2x)2x=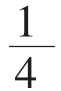 (a-2x)(24x)
(a-2x)(24x)
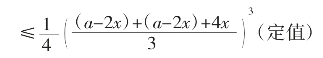
当且仅当a-2x=4x,即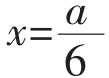 时,V有最大值,最大值是
时,V有最大值,最大值是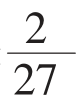 a3。
a3。
由此可得出结论,若n个正数的和一定,则这n个正数相等时,它们的乘积最大。
问题二:制作一个圆柱形易拉罐(有底有盖),当容积一定时,尺寸如何设计,才能使制作用料最省(如图4)。
分析:问题实质上是求圆柱的容积一定时,何时圆柱体表面积取最小值?
设圆柱的底面半径为r,高为h,容积为V(定值),
则V=πr2h
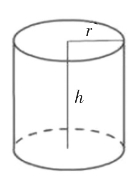
图4
圆柱表面积为S=2πr2+2πrh=2π(r2+rh)
由均值不等式可知
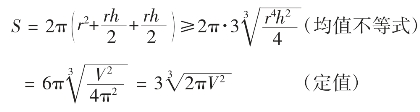
上式当且仅当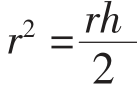 ,即h=2r时,也就是圆柱的高和底面直径相等时,S取最小值,此时用料最省。
,即h=2r时,也就是圆柱的高和底面直径相等时,S取最小值,此时用料最省。
用料最省、成本最低,实际上就是在数学关系上求最小值问题。
又例如:体积一定的正方体、等边圆柱(轴截面是正方形)、球中,表面积最小的是球。
例5:两个自然数的积是48,这两个自然数是什么值时,它们的和最小?
分析:48的约数从小到大依次是1,2,3,4,6,8,12,16,24,48。所以,两个自然数的乘积是48与其和的情形,共有以下5种:
48=1×48,1+48=49;48=2×24,2+24=26;
48=3×16,3+16=19;48=4×12,4+12=16;48=6×8,6+8=14。
显然,两个因数之和最小的是6+8=14。
结论:两个自然数的乘积一定时,两个自然数的差越小,这两个自然数的和也越小。特别的,如果两个数能相等时,这两个数的和最小。
在上面的问题中,如果不要求是自然数时,则当且仅当分成的两个数都是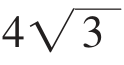 时,其和最小,最小是
时,其和最小,最小是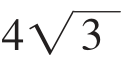 +
+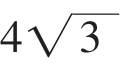 =
=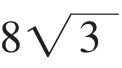 ≈13.856,而
≈13.856,而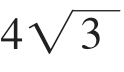 ×
×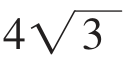 =48。
=48。
这个问题还可以推广,也就是说,n个正数的乘积是定值,则n个正数的和一定有最小值。即:
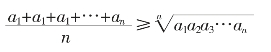
其中a1,a2,a3,…,an都是正数。
当且仅当a1=a2=a3=…=an时,上式取“=”。
此时,a1+a2+a3+…+an取最小值,最小值为na1。
例如,体积一定的长方体中,正方体的表面积最小。
设长方体的长、宽、高分别为a,b,c,则体积为abc=V(定值),
那么其表面积为:S=2(ab+bc+ac)
因为S=2(ab+bc+ac)≥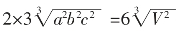
当且仅当ab=bc=ac,即a=b=c时,S取最小值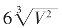 ,此时长方体为正方体。
,此时长方体为正方体。
例6:有一类自然数,它的各个数位上的数字之和为2018,那么这类自然数中最小的是几?
分析:一个自然数的值要最小,首先要求它的位数最少,其次要求高位的数值尽可能地小。由于各个数位上的和固定为2018,要想数位最少,各个位数上的数就要尽可能多地取9,
而2018÷9=224……2
所以满足条件的最小自然数的最高位数应该是2,其后为224个9,
即
问题三:如图5,一条两岸基本平行的河流,河的两岸有A、B两个村庄,现在河上架一座桥,并分别修一条通向村庄的公路。试问大桥建在何处,使得从A到B的路程最短?
分析:如图5,大桥若建在EF处,EF垂直于河岸,EF也是河的宽度,则从A到B的总路程为:AF+FE+EB,
此时大桥FE的长度是不变的,变化的是AF和EB。
问题转化为AF+FE+EB何时最短?
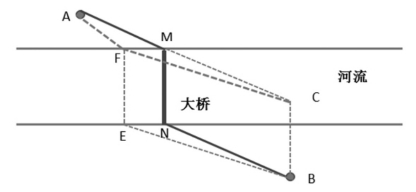
图5
方法一:过B点做线段BC垂直于河岸,且BC=EF,连接AC交河岸一侧于M,做MN垂直于河岸交另一河岸于N,再连接NB,
则只需把大桥建在MN处,则从A到B的路程AM+MN+NB最短。
因为在图中,FE=MN,FC=EB,MC=NB,
所以,AF+FE+EB=AF+MN+FC≥AC+MN=AM+MC+MN=AM+MN+NB
所以,AM+MN+NB就是最短的距离。
方法二:如图6,做A点关于河岸L1的对称点A′,同样过B点作关于整个河流的对称点B′(即BB′垂直于河的两岸,且B′、B,到各自河岸的距离相等),连接A′B′,交河岸L1于M点,过点M作MN垂直于河岸交河岸L2于N点,MN即为建桥的位置,连接AM、NB,则从A到B的最短路程为AM+MN+NB。
证明方法参考方法一。
类似的,如果有两个村庄在一条河的同岸,如图7中的A、B,要在与村庄同侧的河岸边修建一个水塔,使其到两个村庄的距离之和最短,那么水塔应该修在何处?
同样的方法,做B点关于河岸L的对称点C,连接AC,交河岸L于P点,P点即为所求。也就是说AP+PB最短,这是因为:
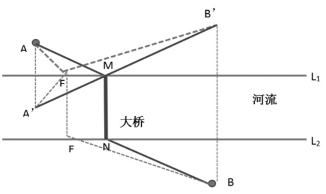
图6
若水塔建在M点,则AP+PB=AP+PC=AC≤AM+MC=AM+MB
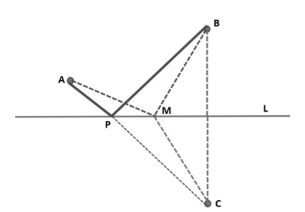
图7
所以,AP+PB最短。
例7:聪明的蜘蛛。如图8,在一个长、宽、高分别为4、3、2的长方体盒子中,一只蜘蛛从A点出发,沿长方体表面爬到C′点,蜘蛛总是走的路程最短,你知道蜘蛛是怎样走的吗?最短路程是多少?
分析:如图,在长方体ABCDA′B′C′D′中,AD=4,DC=3,CC′=2。
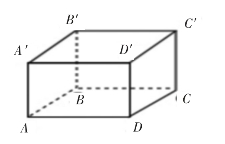
图8
要求蜘蛛爬行的最短路程,需将长方体的侧面展开,进而根据“两点之间线段最短”得出结果。
下面分三种情况把长方体剪开,来分别研究它们的路程。
解:第一种情况,如图9,把长方体剪开,拼成长方形ACC′A′,宽为AA′=2,长为AD+DC=4+3=7,连接AC′即为蜘蛛可能走的路线之一,因为ACC′构成直角三角形,由勾股定理得:
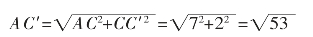
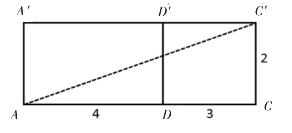
图9
这是不是最短距离呢?还不一定。
第二种情况,如图10,把长方体剪开拼成长方形ADC′B′,宽为AD=4,长为DD′+D′C′=5,连接AC′,则A、D、C′构成直角三角形,同理,由勾股定理,得AC′= 。
。
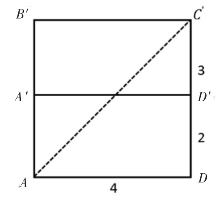
图10
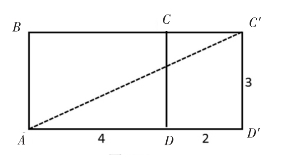
图11
第三种情况,如图11,把长方体剪开拼成长方形AD′C′B,宽为AB=3,长为AD+DD′=6,连接AC′,则A、D′、C′构成直角三角形,同理,由勾股定理,得AC′= =3
=3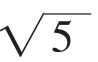 。
。
∴蜘蛛从A点出发穿过A′D′到达C′点路程最短,最短路程是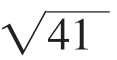 。
。
因此,不管在什么背景下,有关线段之和的最短问题,总是化归到“两点之间的所有连线中,线段最短”,而转化的方法大都是借助于“轴对称点”的几何模型,或通过展开成平面图形找最短的线段。
例8:如图12,圆锥的底面半径为1,母线长为4,一只蚂蚁要从底面圆周上一点B出发,沿圆锥侧面爬行一圈再回到点B,问它爬行的最短路线长是多少?
分析:将圆锥的侧面展开,展开图为扇形ABB′,如图所示。
如果蚂蚁沿底面爬一周回到B点,其路线为展开图中的BB′弧。在展开图中,连接BB′,显然BB′为蚂蚁爬行的最短路线(因为BB′是直线段)。
因为,圆锥的底面半径为1,母线长为4,
所以,∠BAB′=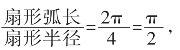
所以△ABB′是直角三角形。
由勾股定理可知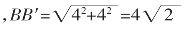
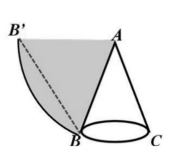
图12
因此,蚂蚁爬行的最短路线长为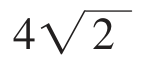 。
。
最后我们再来看一个实际问题。
例9:某地有甲、乙、丙三个不在同一直线上的村庄,当地政府计划修建一座水塔向三个村庄集中供水,试问水塔修建在何处,可使铺设的总输水管道最省?
用数学问题表述就是:在三角形内找一点,使其到三个顶点的距离之和最短。
即:已知△ABC,在其中确定一点P,使P到三顶点的距离之和PA+PB+PC最小。
费马曾最早提出过这个问题,并给出了解决方案,所以人们称这个点为“费马点”。
费马还证明这个特殊的点对于每个给定的三角形不但存在而且只有一个。
那么如何确定费马点呢?
下面分两种情况来说明费马点的确定。
(1)若三角形三个内角均小于120°,那么费马点到三顶点的距离连线正好三等分费马点所在的周角,即该点所对三角形三边的张角相等,即∠BPC=∠BPA=∠APC=120°。所以三角形的费马点也称为三角形的等角中心。
(2)若三角形有一内角大于等于120°,则此钝角的顶点就是距离和最小的费马点。
那么如何用尺规作图法找到费马点呢?
我们只考虑三角形的三个内角均小于120°的情况。
解法如下:分别以AB、AC为边向外侧作正三角形ABD、ACE,连结CD、BE交于一点P,则点P即为所求的点。
证明:如图13所示,连结PA、PB、PC,在△ABE和△ACD中,
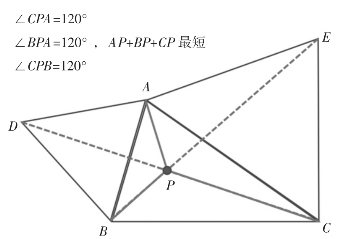
图13
AB=AD,AE=AC,∠BAE=∠BAC+60°,∠DAC=∠BAC+60°,
∴∠BAE=∠DAC
∴△ABE≌△ADC
∴∠ABE=∠ADC从而A、D、B、P四点共圆
∴∠APD=∠ABD=60°,∠APB=120°,
同理:∠APC=∠BPC=120°。
所以,此时的点P就是费马点。
前面我们已经证明了费马点到三角形三个顶点的距离之和最小。因此水塔只需修在费马点的位置上,可使铺设的总输水管道最省。
总之,数学来源于生活,又服务于生活,又高于生活。数学的发展是科技发展的前提,也是人类文明发展的基础,尤其是当今的大数据时代,数学有着其无法替代的作用,也是现代人必备的、重要的基本素养之一。
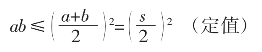
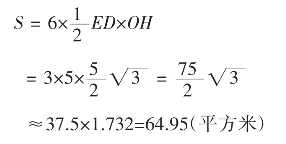

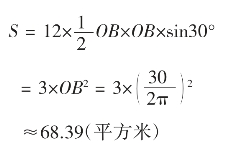
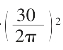 =71.62(平方米)
=71.62(平方米)

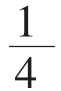 (a-2x)(
(a-2x)(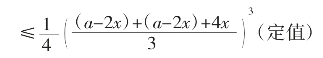
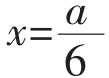 时,V有最大值,最大值是
时,V有最大值,最大值是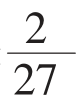 a
a
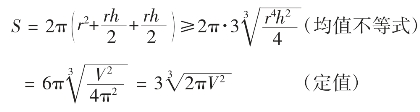
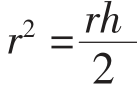 ,即h=2r时,也就是圆柱的高和底面直径相等时,S取最小值,此时用料最省。
,即h=2r时,也就是圆柱的高和底面直径相等时,S取最小值,此时用料最省。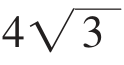 时,其和最小,最小是
时,其和最小,最小是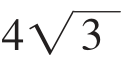 +
+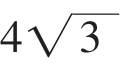 =
=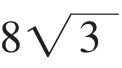 ≈13.856,而
≈13.856,而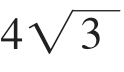 ×
×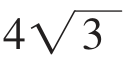 =48。
=48。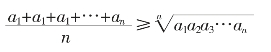





 。
。

 =3
=3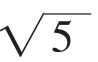 。
。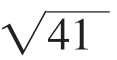 。
。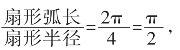

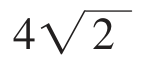 。
。