全屏显示专题章节

自然数的四则运算是算术中最基本的数学运算，也是我国小学数学的主要内容。在我国，两位数以上的四则运算，多以列竖式从低位到高位的运算顺序来进行，这也是很多国家最常用的运算方法。但自然数的运算中也有其无穷的奥妙，有很多运算，算法巧妙，运算速度快，甚至无需列竖式，直接口算即可，如印度数学的计算体系中就包含着很多巧妙的算法。

古印度是世界四大文明古国之一，从公元前2500年至公元1500年之间创造了灿烂的印度河文明。印度数学的起源也和其他古老民族的数学起源一样，是在生产实际需要的基础上产生的。但是，古代印度人有着超人的数学天赋，他们发明了现今世界通用的阿拉伯数字，还首先发现使用了数字“0”，构建了比较完整的算术运算体系，使算术运算变得简单明了，大大提高了运算效率。与此同时，印度人还创造了从高位到低位的快速运算方法和一些特殊的运算技巧。如计算75×75=？你能瞬间算出这道数学题的答案吗？了解了印度数学的计算方法，2秒钟就可以给出答案。也许你会惊讶，“这是数学还是魔术？”但是，真的就这么神奇！事实上，至今印度人的数学能力在全世界都是首屈一指的。

印度的数学来源于古代印度的《吠陀算经》，所以又称吠陀数学。印度数学家在《吠陀算经》的基础上重构了数学计算体系，并将其传播到世界各地。吠陀数学最大的特点是快速而准确，比一般的计算方法快10～15倍，其结构连贯、完美、准确且容易计算。理解了吠陀数学的运算法则，便可以创造出自己的解题方法。

本篇重点以两位数的运算为例来阐述印度数学的算法，可谓是吠陀数学的入门篇。如果你能把这些简单又神奇的法则熟记于心，这将会成为以后进行熟练运算的基础，也可能会使你成为最酷的数学达人！

1.速算加法我们通常的加法运算是从右侧个位数加起，逢十进一，这种算法较慢。而印度数学是从左侧算起，不用考虑进位，大大提高了运算的速度与准确度。

例1：计算87+65。

计算方法：首先十位加十位，即8+6=14，然后个位加个位，7+5=12，

所得的结果再错位相加即得。即4在十位，2在个位，其和为152。

用竖式直观表示如下：

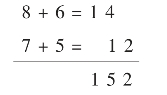
或87+65=（80+60）+（7+5）=140+12=152。

例2：计算467+358。

4+3=7，6+5=11，7+8=15，7在百位，1在十位，5在个位，其和为825；

或467+358=467+300+50+8=767+50+8=817+8=825。

例3：补数运算法。能将一个数凑成整十、整百、整千之类的数的数，称为补数。如2就是98的补数，和是100。6是994的补数，和是1000。运用补数是印度数学运算的一个重要秘诀，可以提高运算的速度和准确率。

如：98+67=（98+2）+65=100+65=165

　　295+468=（295+5）+463=763

主要是需要借位的减法速算，其算法是：

①将被减数分解成两部分：整十、整百或整千（小于被减数）和余下的数（余数）；

②将减数也分成两部分：整十倍的数（大于减数）和补数；

③将前两步的整十倍数相减，将余数和补数相加，把这两个结果相加即得。

例1：计算54-28。

被减数分成50和4，减数分成30和2，50-30=20，4+2=6，

结果是：20+6=26，即54-28=26。

例2：92-54=（90-60）+（2+6）=38

例3：713-396=（700-400）+（13+4）=317

3.速算两位数的乘法

类型1：个位数是5的两位数的平方。

如计算352，只需用十位数3乘以比它大1的数4得12，作为最高位的两位数，然后并上个位数5的平方25即得其结果，即352=1225。

又如计算752，7×8=56，5×5=25，所以752=5625。

同样，952=9025。

原理：设个位数是5的两位数为10a+5（a是1～9的自然数），

则（10a+5）2=100a2+100a+52=100a（a+1）+25。

推广：1052，10×11=110，所以1052=11025；

　　　1152=？因为11×12=132，1152=13225。

下面我们来看大家都十分熟悉的一道有名的算式：

1+2+3+4+5+…+100=5050

但是对于算式13+23+33+43+53+…+1003=？

我们也有一个著名的关系式：

13+23+33+43+53+…+1003=（1+2+3+4+5+…+100）2

而对于50502，我们就可以用以上简便的方法得到。用50×51=2550，502=2500，所以，50502=25502500。

即13+23+33+43+53+…+1003=25502500

类型2：十位数字相同、个位数字之和为10的两位数的乘法。

如23×27，十位数字都是2，个位数字之和是3+7=10，其计算方法是：十位数字乘以比它大1的数，即2×3=6，作为最高位数字，然后并上个位数字相乘所得的积，即3×7=21，即为所求的积，也就是23×27=621；

又如42×48，4×5=20，2×8=16，所以42×48=2016；

再比如74×76，7×8=56，4×6=24，所以，74×76=5624。

同样，93×97=9021，91×99=9009。

原理：设满足条件的两个两位数分别为10a+b，10a+（10-b），

则，（10a+b）［10a+（10-b）］=100a2+10ab+100a-10ab+10b-b2

　　　　　　　　　　　　　　=100a（a+1）+b（10-b）

类型3：任意两位数的平方（除去个位数是5的）。

分两类来处理，一类是个位数小于5的，被10除所得的余数就称为“余数”，如34的余数为4。另一类是个位数大于5的，其个位数加几后就能被10整除的数称为“补数”，如47的补数是3。具体计算方法是：

①情形1：个位数小于5的，如342=？

其算法是，本数加余数，乘以本数的整十，再加上余数的平方即得所求的结果。

即，342=（34+余数）×30（整十的数）+42（个位数的平方）=1156；

又如：532=（53+3）×50+32=2809，722=（72+2）×70+22=5184

②情形2：个位数大于5的，如262=？

其算法是，本数减补数，乘以本数加补数的整十，再加上补数的平方即可得。

即，262=（26-补数）×30（补数后的整十）+42（补数的平方）=676；

又如：482=（48-2）×50+22=2304

　　　872=（87-3）×90+32=7569

类型4：两位数的十位数字相同，个位数字任意。

其算法是：第一个数加上第二个数的个位数（交换两数的位置也可），乘以两位数的整十，再加上两数的个位数相乘，其结果便是所求的积。

即，23×28=（23+8）×20+3×8=620+24=644。

再看几例：43×49=（43+9）×40+3×9=2107，

或43×49=（49+3）×40+3×9=2107 74×73=（74+3）×70+3×4=5402

类型5：任意数和11相乘。

口诀：“两边一拉，邻位相加”。即把和11相乘的数的首位和末位数字拆开，中间留出若干空位；然后把这个数各个数位上相邻的数字依次相加；再把步骤2求出的和依次填写在步骤1留出的空位上。如果相邻数字之和大于10，就向前进一位。

把和11相乘的数的首位和末位数字拉开，中间留出一个空位，即1（）2，然后把这个数各个数位上相邻的数字相加，即1+2=3，把3填写在步骤1留出的空位上，即得132，也就是12×11=132。

也有人把这种算法总结为“两边一拉，中间相加”。

把58拉开，留出一个空位，即5（）8，而5+8=13，括号内填3，1向前进一位，得58×11=638。

推广：213×11=？

把和213的首位和末位数字拉开，中间留出2个空位，即2（）（）3，再把这个数各个数位上的数字依次相加，即2+1=3；1+3=4，把求出的和依次填写在上面留出的空位上，即得2343，亦即213×11=2343。

由上面几例可以看出，两位数乘11，两边拉开后中间空一位，三位数拉开后空两位，以此类推，四位数拉开后空三位，等等。

例3：72586×11=？

把和11相乘的数的首位和末位数字拉开，中间空出四位，即7（）（）（）（）6，把这个数各个数位上的数字依次相加，即7+2=9；2+5=7；5+8=13；8+6=14，把求出的和依次填写在留出的空位上，超过10的向上进一位，即得：798446，也就是72586×11=798446。

类型6：个位是5的数与偶数相乘。

①偶数除以2或4或8；

②个位是5的数相应地乘以2或4或8；

③将前两步的结果相乘。

第一步，22除以2，得22÷2=11；

第二步，用2×15=30；

第三部，将前两步的结果相乘。

例如：24×25=6×4×25=6×100=600

36×35=9×2×2×35=9×2×70=2×630=1260

推广：48×125=6×8×125=6×1000=6000

36×225=9×4×225=9×900=8100

类型7：两个数的平均数是整十的两位数相乘。

①找到被乘数和乘数的平均数，也就是那个整十，并求这个数的平方；

②求被乘数（或乘数）与平均数的差，并求差的平方；

③将前两步的结果相减即得。

例如：79×81，79与81的平均数是80，80的平方是6400，81与80的差是1，1的平方还是1，故79×81=6400-1=6399。

又如：38×42=（40+2）（40-2）=402-22=1596

推广：95×105=（100-5）（100+5）=1002-52=9975 998×1002=10002-22=999996

上面的运算其实就是初中平方差公式的运用，

即（a+b）（a-b）=a2-b2

类型8：至少有一个乘数接近100的两位数乘法。

①以100为基数，分别找到被乘数和乘数的补数；

②用被乘数减去乘数的补数，或者乘数减去被乘数的补数，把差写下来；

③两个补数相乘；

④将步骤3的得数直接写在步骤2的得数后面即可，如超过100可向前进一位。

分别找到被乘数和乘数关于100的补数，即100-78=22，100-97=3；

用被乘数减去乘数的补数，或者乘数减去被乘数的补数，即78-3=75，然后两个补数相乘，即22×3=66；将66直接写在75的后面即可，即7566，也就是78×97=7566。

又如：64×89，64（被乘数）-11（89的补数）=53，补数相乘36×11=396，则乘积结果是5696；

26×98，由于26-2=24，74×2=148，所以26×98=2548。

类型9：100~110之间的整数的乘法。

①被乘数加上乘数个位上的数字；

②个位上的数字相乘；

③将步骤2的得数直接写在步骤1的得数后面。

被乘数加上乘数个位上的数字，即104+7=111；个位上的数字相乘，4×7=28；将两数并写，即得11128，也就是104×107=11128。

又如：102×108，102+8=110，2×8=16，所以，102×108=11016；

107×107，107+7=114，7×7=49，107×107=11449。

下面让我们来欣赏几组特殊的运算：

上式的特点是，左边是只有1组成的数字的平方，右边的结果是“回文数”。

上式左面的被乘数12345679叫做“缺8数”，这个“缺8数”有许多让人惊讶的特点，如上面用9的倍数与它相乘，乘积竟会是由同一个数字组成的，人们把这叫做“清一色”。

③你知道123456789通过什么样的运算就可以倒过来吗？

即变为987654321，请看下面的算式：

123456789×8+9=987654321

神奇的运算还有很多，我们来看两则小故事。

4.印度速算超人拉马努金

斯里尼瓦瑟·拉马努金（泰米尔语：1887年12月22日—1920年4月26日）是印度历史上非常璀璨耀眼的、最著名的数学家之一。他没受过正规的高等数学教育，但沉迷于数论，尤爱牵涉π、质数等数学常数的求和公式，以及整数分拆。惯以直觉跳跃导出公式，他留下的那些没有证明的公式，引发了后来的大量研究。

拉马努金生于印度东南部泰米尔纳德邦的埃罗德，和大文豪泰戈尔是同乡。在1898年十岁的时候，进入贡伯戈讷姆一所中学，在那里他似乎第一次接触到正规的数学。在11岁时，他已经掌握了住在他家的房客的数学知识，他们是政府大学的学生，到13岁，他就掌握了借来的高等三角学的书里的知识，他的天才在14岁时开始显露。

1913年，拉马努金发了一长串复杂的定理给剑桥的三个学术界著名人士贝克（H.F.Baker）、霍布森（E.W.Hobson）和哈代（G.H.Hardy），但只有三一学院的院士、英国著名数学家哈代注意到了拉马努金定理中所展示的天才。虽然哈代是当时著名的数学家，而且是拉马努金所写的众多定理中几个领域中的专家，但他还是说很多定理“完全打败了我”，“我从没见过任何像这样的东西。”他还说：“只要看它们一眼就知道只有第一流的数学家才能写下它们。”哈代说他自己对数学最伟大的贡献就是发现了拉马努金，并把拉马努金的天才比作至少和数学巨人欧拉和雅可比相当。拉马努金后来也成为剑桥三一学院的院士，并得到了科学界最高级别的荣誉——英国皇家学会会员（FRS）。

拉马努金是印度在过去一千年中所出的非常伟大的数学家。他的直觉的跳跃甚至令今天的数学家也感到迷惑，他的定理被应用到很多很难想象到的众多领域。

一次，拉马努金身患重病，哈代前往探望。哈代说：“我乘计程车来，车牌号码是1729，这个数真没趣，希望不是不祥之兆。”拉马努金答道：“不，那是个很有趣的数字，可以用两个立方之和来表达，而且只有两种这样的表达方式，且用这种方式表示的数之中，1729是最小的，即1729=13+123=93+103。”后来这类数被称为的士数。拉马努金超强的心算能力，令哈代大为吃惊，他惊叹道：“每个自然数都是拉马努金的朋友。”

印度人惊人的数学才能得益于这个民族对数学的特别领悟和印度吠陀数学神奇的计算方法。

再来看一个有趣的故事。

5.数学魔女沙贡塔娜

1981年的一个夏日，在印度举行了一场心算比赛。一位教授走上讲台，简短的致词后，在黑板上写下了一个201位的大数，心算的要求是：在短时间内算出这个数字的23次方根。挑战者是37岁的沙贡塔娜，她是印度的一位普通妇女，沙贡塔娜上台了，当天，她要以惊人的心算能力，与一台先进的电子计算机展开竞赛。

教授用4分钟写完这个大数。然后，沙贡塔娜便开始心算。与此同时，电子计算机也进行工作。沙贡塔娜仅用50秒完成了心算题目，向观众报出了正确的答案。而计算机恰恰相反，为了算出得数，它必须输入两万多条指令，才能开始计算，时间自然比沙贡塔娜慢得多。

大厅中爆发出暴风雨般的掌声和热烈的欢呼声，人们祝贺沙贡塔娜所取得的成功。这一奇闻，曾在国际上引起了轰动，沙贡塔娜被称为“数学魔术家”。