银行利率与自然常数e
居民在银行存款是最常见、最普遍的理财方式之一。银行存款的方式有多种形式,利率也各不相同,如活期存款、整存整取、零存整取等,当然也还有专门的理财产品。熟悉银行的存款方式,会进行银行利息的计算,对于居民合理选择存款来增加收益非常重要,这是生活中最典型的数学应用之一。
存入银行的钱叫做本金,取款时银行多支付的钱叫做利息,利息与本钱的比值叫做利率。
利率通常用百分比表示,按年计算则称为年利率,按月计算则称为月利率。
其计算公式是: 。
。
乘100%是为了将数字切换成百分率,与乘1的意思相同,计算中可不加,只需记住即可。关于时间,大多数银行是按每月30天、每年360天来计算的。
如果用i表示利率、用l表示利息额、用p表示本金,t表示存入时间,则利率可用公式表示为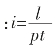 。
。
若t表示月数,则公式计算的结果是月利率,若t表示年数,则计算结果是年利率。
如存入本金1000元,三年后得本息和是1127元,则可知当年的三年定期利率是:
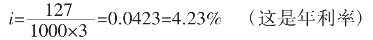
一般来说,利率根据计量的期限标准不同,表示方法有:年利率、月利率、日利率等。
根据国家的经济发展水平,利率也会进行适时的调整。
我们来看日常存款利息的计算方法。
1.存款本利计算方法
(1)整存整取
整存整取是指开户时约定存期,一次性存入,届时一次性支取本息的一种个人存款方式。50元起存,外汇起存金额为等值于人民币100元的外汇。计息按存入时的约定利率计算,利随本清。
人民币存期(定期)分为三个月、六个月、一年、两年、三年、五年六个档次。外币存期分为一个月、三个月、六个月、一年、两年五个档次。
整存整取存款本息可以在到期日自动转存,也可根据客户意愿到期办理约定转存。
整存整取利息计算公式为:
利息=本金×利率×实际月数/12。
假如存入一万元人民币,某一个时期的利率是:
三个月是2.85%,半年是3.05%,一年是3.25%,二年是4.4%,三年是5.0%,五年是5.5%;其利息的计算结果是:
三个月的利息计算公式=10000×2.85%×3÷12=71.25元;
半年的利息计算公式=10000×3.05%×6÷12=152.50元;
一年的利息计算公式=10000×3.25%×1=325元;
二年的利息计算公式=10000×4.4%×2=880元;
三年的利息计算公式=10000×5.0%×3=1500元;
五年的利息计算公式=10000×5.5%×5=2750元。
在此需要说明的是,上述公式中所说的“利率”一般可分为年利率、月利率和日利率。年利率用百分之几表示,月利率用千分之几表示,日利率用万分之几表示。其中:
日利率(‰0)=年利率(%)÷360
月利率(‰)=年利率(%)÷12
另外,在日常生活中,利率也经常用分、厘、毫表示,那么我们该如何理解呢?
如:“年息9厘”其实就是说“年利率9%”,即每百元存款1年利息9元;“月息1分”其实就是说“月利率10‰”,即每千元存款1月利息10元;“日息1厘5毫”其实就是说“日息1.5‰0”,即每万元存款每日利息1元5角。
(2)零存整取利息的计算
零存整取是居民普遍采用的存款方法之一。零存整取的余额是逐月递增的,因而我们不能简单地采用整存整取的计算利息的方式,只能用单利年金方式计算,公式如下:
Sn=A(1+R)+A(1+2R)+…+A(1+nR)=nA+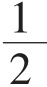 n(n+1)AR
n(n+1)AR
其中,A表示每期存入的本金,R是利率,Sn是n期后的本利和,Sn又可称为单利年金终值。上式中,nA是所储蓄的本金的总额,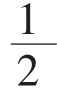 n(n+1)AR是所获得的利息的总数额。
n(n+1)AR是所获得的利息的总数额。
通常,零存整取是每月存入一次,且存入金额每次都相同,因此,为了方便起见,我们将存期可化为常数如下:
如果存期是1年,那么令D=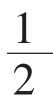 n(n+1)=
n(n+1)=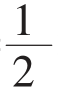 ×12×(12+1)=78,同样,如果存期为2年,则常数由上式可算出D=300,如果存期为3年,则常数为D=666。
×12×(12+1)=78,同样,如果存期为2年,则常数由上式可算出D=300,如果存期为3年,则常数为D=666。
这样算来,就有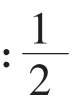 n(n+1)AR=DAR,即零存整取利息。
n(n+1)AR=DAR,即零存整取利息。
例如:你每月存入1000元。存期为1年,存入月利率若为1.425‰(根据银行当年的利息标准为依据,不同时期标准会有变化),则期满年利息为:1000×78×1.425‰=111.15(元)。
零存整取还有另外一种计算利息的方法,这就是定额计息法。
所谓定额计息法,就是用积数法计算出每元的利息化为定额息,再以每元的定额息乘以到期结存余额,就得到利息额。
每元定额息=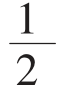 n(n+1)AR÷nA=
n(n+1)AR÷nA=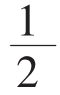 (n+1)R
(n+1)R
如果,银行一年期的零存整取的月息为1.425‰。那么,我们可以计算出每元的定额息为:1/2×(12+1)×1.425‰=0.0092625。
假如你每月存入1000元,此到期余额为:1000×12=12000(元)
则利息为:12000×0.0092625=111.15(元)。
同样,人们在发展生产、改善生活中也离不开贷款,如贷款建厂、贷款建房、贷款买车、贷款买房等。那么贷款利息又是如何计算的呢?
2.贷款利息计算方法
以涉及千家万户的房贷为例,看看个人住房按揭贷款是如何计算的。个人住房按揭贷款,其还本付息方法通常有两种。
(1)等额本息还款计算方法
等额本息贷款的还款方法,即把按揭贷款的本金总额与利息总额相加,然后平均分摊到还款期限的每个月中,每个月的还款额是固定的,但每月还款额中的本金比重逐月递增、利息比重逐月递减。其计算公式为:
每月还款金额(简称每月本息)=
还款月数=贷款年限×12
月利率=年利率/12。
下面给出两种简单的推导方法。
方法一:设贷款本金为A,月利率为r,还款月数为n,每月还款金额为x,那么,每月所还款的本利和累计为在约定期内贷款的本利和,即
x+x(1+r)+x(1+r)2+…+x(1+r)n-1=A(1+r)n
∴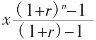 =A(1+r)n
=A(1+r)n
所以,x=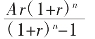
方法二:设Bk为第k个月末还款后尚欠银行的本利和,则
B1=A(1+r)-x
B2=B1(1+r)-x=A(1+r)2-x(1+r)-x
B3=B2(1+r)-x=A(1+r)3-x(1+r)2-x(1+r)-x
……
Bn=Bn-1(1+r)-x=A(1+r)n-x(1+r)n-1-…-x(1+r)-x
=A(1+r)n-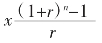
因Bn=0,得
本息还款法的计算原则:银行从每月月供款中,先收剩余本金利息,后收本金。利息在月供款中的比例中随剩余本金的减少而降低,本金在月供款中的比例因增加而升高,但月供总额保持不变。
特点:本金逐渐增加。
所谓等额本息还款,就是指贷款期限内每月以相等的金额偿还贷款本息,直至结清贷款。即借款人归还的利息和本金之和每月都相等,利息和本金占计划月还款额的比例每次都发生变化,开始时由于本金较多,因而利息占的比重较大,当期应还本金=计划月还款额-当期应还利息,随着还款次数的增多,本金所占比重逐渐增加。
以贷款20万元20年还清为例,按年利率7.47%计算,月均还款为

支付总利息达185942.8元,还款总额共计385942.8元。
(2)等额本金还款计算方法
即借款人每月按相等的本金额(贷款金额/贷款月数)偿还贷款本金,每月贷款利息按月初剩余贷款本金计算并逐月结清,两者合计即为每月的还款额。其计算公式为:
每月还款金额= +(本金-累计已还本金额)×月利率
+(本金-累计已还本金额)×月利率
累计已还本金=已经归还贷款的月数×贷款本金/还款月数
等额本金利息计算原则:每月归还的本金额始终不变,利息会随剩余本金的减少而减少。
特点:利息由多渐少。
等额本金还款方式则指每月等额偿还本金,贷款利息随本金减少逐月递减直至结清贷款。即每月归还本金的数额相等,利息=当期剩余本金×月利率,每月的还款额并不固定,而是随着每月本金的减少而递减,随着还款次数的增多,利息由多逐渐减少。
同样以贷款20万元20年还清为例,按年利率7.47%算,第一个月还款本金为833.33,利息为1245,共计还款2078.33元。第二个月还款为2073.14元,以后每月递减,最后一个月还清时还款838.52元。支付总利息为150022.5元,还贷总额为350022.5元(显然要比等额本息还款少3万5千余元)。
这两种计算方法不尽相同,也就是说,等额本息还款法实际上是等比数列,等额本金还款法是等差数列。等额本息还款采用的是复合利率计算,在每期还款的结算时刻,剩余本金所产生的利息要和剩余的本金(贷款余额)一起被计息,也就是说未付的利息也要计息。
然而,等额本金贷款采用的是简单利率方式计算利息。在每期还款的结算时刻,它只对剩余的本金(贷款余额)计息,且未支付的贷款利息不与未支付的贷款余额一起作利息计算,而只有本金才作利息计算。
贷款周期越长,等额本息贷款就要比等额本金贷款产生越多的利息。所以,贷款周期越长的借款人,应该优先选择等额本金贷款。
两种方式,各有优势。
同样20万元还20年,等额本息还款利息比等额本金还款多35782.2元。如果贷款100万,那就会多出178911元。显然,“本金”的利息明显低于“本息”,可是,是否“本金”还款是最佳选择呢?
银行分析人士说,“本息”还款优点是每月偿还金额相等,还款压力均衡,便于借款人合理安排家庭收支计划,对于精通投资、善于理财的家庭,无疑是最好的选择。只要投资回报率高于贷款利率,则占用资金的时间越长越好,这种还款法还适合未来收入比较稳定或略有增加的借款人,如部分年轻人、资金较为紧缺,但未来有能力提前还贷,这样利息也会相对减少。
“本金”还款法在贷款初期月还款额大,还贷压力较重,尤其是在贷款总额比较大的情况下,相差上千元。但是,随着时间推移,还款负担逐渐减轻。适合收入较高,有一定的经济基础,但是预计将来负担会加重的人群。
等额本息还款法,之所以利息比较高,实际上是一种“复利”计算方法。
3.复利
所谓的复利是指在每经过一个计息期后,都要将所生利息加入本金,以计算下期的利息。这样,在每一个计息期,上一个计息期的利息都将成为生息的本金,即以利生利,也就是俗称的“利滚利”。
复利计算的特点是:把上期末的本利和作为下一期的本金,在计算时每一期本金的数额是不同的。复利的计算公式是:
S=p(1+i)n
其中,S表示复利终值(本利和),p表示本金,n表示计息期数,i表示利率。
假设本金1000元,在年利率为5%的情况下每半年计息一次,问在复利计息的情况下,二年后本利和是多少?
其计算方法是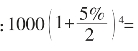 1103.81元。这就是过去所谓的利滚利。
1103.81元。这就是过去所谓的利滚利。
很多投资项目,多以复利进行计算。一方面是复利的高回报率,另一方面投资也有风险,需谨慎行事。
例如:一个投资者第一年将积蓄的50000元进行投资,每年都能获得的利率或者投资回报率为3%,他将这些本利之和连同年金(5万)再投入新一轮的投资,投资年限为30年(相当于零存整取,但是复利计算利息),那么,30年后所获得的本利收入,也就是按复利计算公式来计算本利和(终值),他的资产总值将变为:
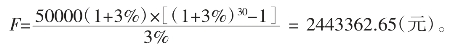
复利的计算与一个重要的常数e有着密切的关系。
我们来举一个复利变化的例子,即如何得到复利的最大化。
假设我们考虑一年的定期存款,初始存款为1万元,假如年利率为100%,当然利率不可能是100%,我们只是为了计算方便,你也可以设置其他的利率,或者真实的利率均可,这不影响我们的计算方法。
第一年结束后,按照所给的利率,本金是1万,利息是1万,总收益是2万;假如半年单独结算一次,利率降低到50%,那么半年后的利息是0.5万元,本利和是1.5万,以此为本金,下半年结束后,所得利息是0.75万元,也就是一年后由最初的1万元增加到了2.25万元。通过半年计算一次利息,比一年结一次利息多出了0.25万元。如果初始存款100万,我们便多出25万的收益。
由此可以看出,在一年的时间里,如果结息的周期缩短,我们将获得更多的收益。不妨将一年划分成四个季度,每个季度结一次息,利率将变成25%,通过复利计算,一年后我们将得到的本利和是(1+25%)4=2.44141万元。我们的收益在增加,再一次说明结息周期越短,我们获得的收益也越大。设想,我们可以将结息周期划分成月,划分成星期,划分成天,划分成小时、分、秒等,是否我们的钱也会无限增长吗?我们会变成百万富翁吗?我们来看下表:
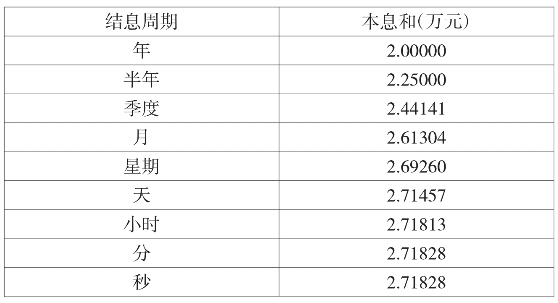
这虽是一个无限递增的过程,但最终使本息和停留在某一个常数上。这个常数,也就是这个极限值被数学家称之为e。e的近似值为2.71828。
和π一样,e既是无理数,也是超越数,是一个非常重要的数学常数,也是数学三大常数之一(圆周率、黄金分割、自然常数),一般我们称其为自然常数。虽然自然常数e的知名度比圆周率π低很多,原因是圆周率更容易在实际生活中遇到,而自然常数e在日常生活中看似不太常用,但是经济增长规律、植物生长规律、动物种群变化等都与e有关,所以俗称“自然数”。e的重要作用还在于数学中的利率计算、对数计算、复数计算中,尤其是在高等数学中更是有着不可忽视的重要作用。
比如融合e、π、i、1、0的最完美的欧拉公式:
eπi+1=0
就是自然常数e的数学价值的最高体现。
那么,我们如何给自然常数e找一个精确的表达式呢?
受复利计算的启发,数学家们得到了一个精确的表达式是:
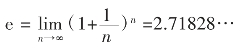
这是一个无限不循环小数,既是无理数,也是超越数。有时也称e为欧拉数(Euler number),是以瑞士大数学家欧拉命名的。
e的小数点后前100位是:
“e≈2.71828 18284 59045 23536 02874 71352 66249 77572 47093 69995 95749 66967 62772 40766 30353 54759 45713 82178 52516 64274”
因为e=2.718281828…,极为接近循环小数2.71828(1828循环),那就把循环小数化为分数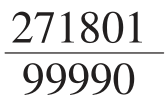 ,所以可以用
,所以可以用 表示为e的最接近的有理数约率,精确度高达99.9999999%。如果限定分子分母都是两位数的话,e的最佳近似值是
表示为e的最接近的有理数约率,精确度高达99.9999999%。如果限定分子分母都是两位数的话,e的最佳近似值是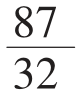 。有趣的是,如果将分母和分子限定到三位数,则最佳近似是
。有趣的是,如果将分母和分子限定到三位数,则最佳近似是 。第二个分数恰好为第一个分数的一个回文展开数。
。第二个分数恰好为第一个分数的一个回文展开数。
e作为重要的数学常数,也是其自然对数的底数。对数中最重要、最常用的两个对数就是自然对数和常用对数,它们的关系是:

即 lg x=lg e·ln x
数学家们还发现,自然常数e还有其他一些表示方法:
如:欧拉首先发现了e的连分数表示:
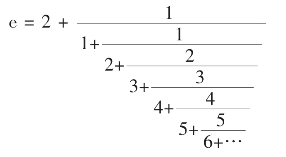
e还有一个著名的展开式(泰勒展开式):

下面让我们简单回顾一下自然常数e的发现历程:
1618年,第一次提到常数e,是约翰·纳皮尔(John Napier)于1618年出版的对数著作附录中的一张表。但它没有记录这常数,只有由它为底计算出的一张自然对数列表。
1683年,第一次把e看为常数的是数学家族中的雅各布·伯努利(Jacob Bernoulli),他在研究复利问题时用到此常数。
1690年,第一次使用常数e,是莱布尼茨于1690年和1691年给惠更斯的通信,当时是用b表示。
1727年,欧拉开始用字母e来表示这个常数。而e第一次在出版物中用到,是1736年欧拉的《力学》(Mechanica)。虽然以后也有研究者用字母c表示,但e最常用,终于成为标准。所以有时也称e为欧拉数。
1737年,欧拉证明了e是无理数。1748年,欧拉将e计算到了小数点后23位;大概在同一时期,欧拉还发现了著名的欧拉公式:eπi+1=0。
1873年,法国数学家埃尔米特证明了e是超越数,这是第一个获证的超越数。9年之后,德国数学家林德曼沿用埃尔米特的方法证明了π是超越数,这个问题更引人注目。
从遇到自然常数e到基本认识e,数学家们也是经过了两百多年的探索和研究。
π和e之间也有着某些特殊的关系,eπ和πe的值非常接近,而且容易证明:eπ>πe,当然,只需用计算器计算一下便可知道,而它们的近似值也分别为:eπ≈23.14069,πe≈22.45916
这其中,数字eπ也是一个重要的常数,称为盖尔范德常数,并且已被证明了是超越数。但πe还没有人证明它是无理数。
e也可以用在函数当中,如很多增长或衰减过程都可以用指数函数来表示。比如说经济增长和人口增长,还有放射性衰变等。而用e做底数的指数函数就是一个重要函数,其重要方面,还在于它是唯一的函数与其导数相等的函数,即
指数函数是y=ex,其导数是y′=ex。
这个函数也被称为是最美的函数,它也是函数的一个中心角色。
而以自然常数为底的自然对数函数,在求导时,也非常简单,如:
对数函数是y=ln x,其导数是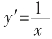 。
。
当然,数字e也出现在与增长无关的地方。有一个例子,说的是一群人去聚餐吃饭,吃完后在离开时随机拿起一顶帽子(假设每个人都有一顶不同的帽子),那么没有人拿到自己帽子的概率有多大?
可以证明这个概率是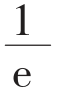 (大约37%),所以至少有一人拿到了自己的帽子的概率为
(大约37%),所以至少有一人拿到了自己的帽子的概率为 (63%)。这也只是在概率的众多运用中的一个例子。还有在统计学中,正态分布的“钟形曲线”涉及e;在工程学中,悬索桥缆索的曲线基于e。这方面的内容可以说是无穷无尽。
(63%)。这也只是在概率的众多运用中的一个例子。还有在统计学中,正态分布的“钟形曲线”涉及e;在工程学中,悬索桥缆索的曲线基于e。这方面的内容可以说是无穷无尽。
由此可以看出,e的重要性是不言而喻的,e也是无可代替的,数学家对其的探究从来就没有停止过,因为它是数学中最自然的数字。
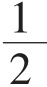 n(n+1)AR
n(n+1)AR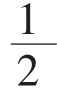 n(n+1)AR是所获得的利息的总数额。
n(n+1)AR是所获得的利息的总数额。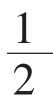 n(n+1)=
n(n+1)=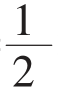 ×12×(12+1)=78,同样,如果存期为2年,则常数由上式可算出D=300,如果存期为3年,则常数为D=666。
×12×(12+1)=78,同样,如果存期为2年,则常数由上式可算出D=300,如果存期为3年,则常数为D=666。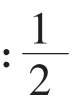 n(n+1)AR=DAR,即零存整取利息。
n(n+1)AR=DAR,即零存整取利息。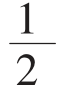 n(n+1)AR÷nA=
n(n+1)AR÷nA=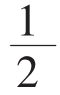 (n+1)R
(n+1)R

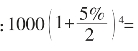 1103.81元。这就是过去所谓的利滚利。
1103.81元。这就是过去所谓的利滚利。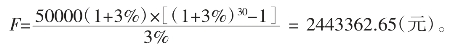

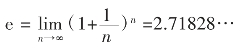
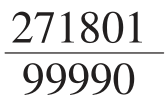 ,所以可以用
,所以可以用 表示为e的最接近的有理数约率,精确度高达99.9999999%。如果限定分子分母都是两位数的话,e的最佳近似值是
表示为e的最接近的有理数约率,精确度高达99.9999999%。如果限定分子分母都是两位数的话,e的最佳近似值是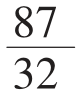 。有趣的是,如果将分母和分子限定到三位数,则最佳近似是
。有趣的是,如果将分母和分子限定到三位数,则最佳近似是 。第二个分数恰好为第一个分数的一个回文展开数。
。第二个分数恰好为第一个分数的一个回文展开数。


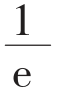 (大约37%),所以至少有一人拿到了自己的帽子的概率为
(大约37%),所以至少有一人拿到了自己的帽子的概率为 (63%)。这也只是在概率的众多运用中的一个例子。还有在统计学中,正态分布的“钟形曲线”涉及e;在工程学中,悬索桥缆索的曲线基于e。这方面的内容可以说是无穷无尽。
(63%)。这也只是在概率的众多运用中的一个例子。还有在统计学中,正态分布的“钟形曲线”涉及e;在工程学中,悬索桥缆索的曲线基于e。这方面的内容可以说是无穷无尽。