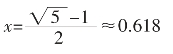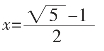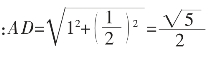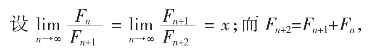黄金分割与华罗庚优选法

有一种特殊的比例关系，在工艺美术和日用品的设计中，经常被采用；在建筑艺术、造型艺术中也具有很高的美学价值。因为按这个比例设计能够引起人们的美感，如古希腊神庙、古埃及金字塔、法国的巴黎圣母院等。这个比例在实际生活中的应用也非常广泛，如国旗的长宽之比，蒙娜丽莎画像的布局，还有舞台上的报幕员并不是站在舞台的正中央，而是偏在台上一侧，以站在舞台宽度的特殊比例点时位置最美观，声音传播得也最好，就连植物界也有很多自然现象也有与此比例相似的地方。如从一棵嫩枝的顶端向下看，就会看到叶子就是按照这种比例的规律排列着的；还有人们在抽签参加比赛时，抽到的排序位置在中间稍靠后一点获奖的几率最大等。在很多科学实验中，这种比例关系，也可以使我们合理地安排较少的试验次数找到科学的配方和合适的工艺条件。正因为这样的比例关系在建筑、艺术、日常生活、工农业生产和科学实验中有着广泛而重要的应用，所以人们把这种特殊的比例称为“黄金分割”。由于黄金分割的普遍性和美丽的比例关系，科学家把它称之为几何学的两大珍宝之一，并认为黄金分割是珍宝中的瑰宝。那么什么是黄金分割呢？

黄金分割（Golden Section）：黄金分割其实是一种特殊的比例关系，是指将整体一分为二，较大部分与整体部分的比值等于较小部分与较大部分的比值，其比值是一个无理数，约为0.618。或者说，把一条线段分为两部分，长段与短段之比恰恰等于整条线段与长段之比，约为1.618∶1或1∶0.618，也就是说长段的平方等于全长与短段的乘积。这种关系具有严格的比例性、艺术性、和谐性，蕴藏着丰富的美学价值。这个比例被公认为是最能引起美感的比例，因此被称为黄金分割。黄金分割数是一个无理数，应用时一般取0.618或1.618，就像圆周率在应用时取3.14一样。

0.618，用数学关系来描述黄金分割，可以得到如下的定义和算式：

已知线段为AB，设其长度AB=1，C是线段AB上的点，

又设AC=x，则CB=1-x，

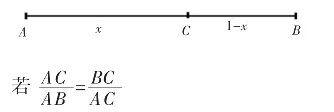
则点C称为线段AB的黄金分割点。

由上式可得x∶1=（1-x）∶x

则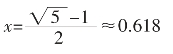

由上面的计算可知，黄金分割的精确值为：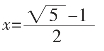

另外x还可用黄金连分数表示：

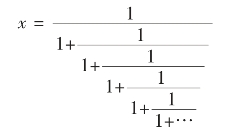
黄金分割数小数点后前32位为：

0.61803398874989484820458683436565

一般应用中，通常取近似值为0.618。

0.618还有一些有趣的运算关系：

1÷0.618≈1.618

（1-0.618）÷0.618≈0.618

1÷（1+0.618）≈0.618

黄金分割值，也称黄金比、黄金数等。

据说黄金分割还有一个古老的传说。在古希腊时代，有一天，古希腊著名学者毕达哥拉斯走在街上，在经过铁匠铺前他听到铁匠打铁的声音非常好听，于是驻足倾听。他发现铁匠打铁节奏很有规律，这个声音的比例被毕达哥拉斯用数学的方式表达出来，就是我们现在所说的黄金分割。

黄金分割最早的记录在公元前6世纪，关于黄金分割比例的发现，大多认为来自古希腊的毕达哥拉斯学派。公元前4世纪，古希腊数学家欧多克索斯第一个系统研究了这一问题，并建立起比例理论。公元前300年左右欧几里得吸收了欧多克索斯的研究成果，进一步系统论述了黄金分割，其《几何原本》成为最早的有关黄金分割的论著。

下面我们来看与黄金分割有关的几个概念和性质。

黄金分割点：是指一条线段分为两部分，使得线段中较长的那部分跟原来整条线段的长的比为黄金比的点称为黄金分割点。一条线段上有两个这样的点。

利用线段上的两个黄金分割点，可以作出正五角星、正五边形等。

我们先看如何用尺规作图得到黄金分割点。

（1）设已知线段为AB，过点B作BD⊥AB，且BD=AB/2；

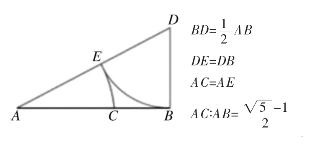
（2）连结AD；

（3）以D为圆心，DB为半径作弧，交AD于E；

（4）以A为圆心，AE为半径作弧，交AB于C，则点C就是AB的黄金分割点。

理由如下：

可设AB=1，则BD=1/2，DE=1/2，

由勾股定理得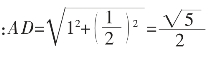

所以，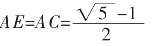

所以C是AB的黄金分割点。

黄金矩形（Golden Rectangle）：如果一个矩形长宽之比是黄金比，也就是矩形的短边比上长边等于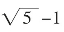（）/2≈0.618，此时长边为短边的1.618倍，就称这个矩形为黄金矩形。事实上，在一个黄金矩形中，以矩形的较短边为边作一个内接正方形，这时，原矩形分成两部分，一个正方形，一个小的新矩形，而这个矩形仍然是一个黄金矩形（如矩形ECDF），这个操作可以无限重复下去，就会产生无数个黄金矩形（如：ECHG，EIKG，JLKG，…）。

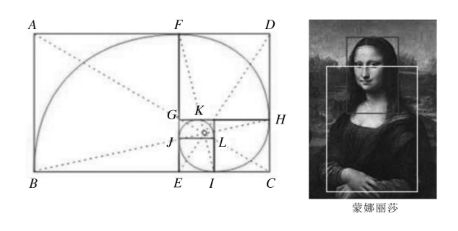
黄金矩形能够给画面带来美感，令人愉悦。在很多艺术品以及大自然中都能找到它，希腊雅典的巴特农神庙就是一个很好的例子。

画家们还发现，按0.618∶1来设计的比例，画出的画最优美，在达·芬奇的作品《维特鲁威人》《蒙娜丽莎》，还有《最后的晚餐》中都运用了黄金分割比。

尤其是《蒙娜丽莎》更是艺术美的完美体现。

黄金分割数列（斐波那契数列）：设一个数列，它的最前面的两个数是1，1，后面的每个数都是它前面的两个数之和。

即：1，1，2，3，5，8，13，21，34，55，89，144，…

这个数列称为“斐波那契数列”，这些数被称为“斐波那契数”。

经计算发现，相邻两个斐波那契数的比值是随序号的增加而逐渐逼近黄金分割比，即f（n）/f（n+1）→0.618…。由于斐波那契数都是整数，两个整数相除之商是有理数，而黄金分割是无理数，所以只是不断逼近黄金分割。但是当我们继续计算出后面更大的斐波那契数时，就会发现相邻两数之比越来越接近黄金分割比。

观察下面的计算：

1÷1=1，1÷2=0.5，2÷3=0.666…，3÷5=0.6，5÷8=0.625，55÷89=0.617977…，144÷233=0.618025…，46368÷75025=0.6180339886…

越到后面，这些比值越接近黄金比，当这个计算趋向于无穷时，

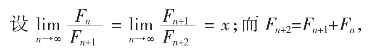
可以得到：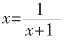

解得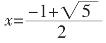，这正是黄金比。

由于其极限是黄金分割比，因此，斐波那契数列又称黄金分割数列。

黄金三角形：所谓黄金三角形是指一个等腰三角形，其底边的长度与腰的长度比为黄金比值，即底与腰的比为（）/2，此三角形被称为黄金三角形。

黄金三角形有2种：

等腰三角形，两个底角为72°，顶角为36°；这种三角形既美观又标准。这样的三角形的底与一腰之长之比为黄金比。

等腰三角形，两个底角为36°，顶角为108°；这样的三角形的一腰与底长之比为黄金比。

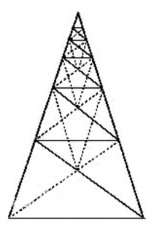
顶角为36°的黄金三角形是一个等腰三角形，它的底与它的腰成黄金比。当底角被平分时，两角平分线分对边也成黄金比，并形成两个较小的黄金三角形，这两个三角形相似于原三角形，类似的也可以产生无数个黄金三角形（如右图）。

正五角星：将一个正五边形的所有对角线连接起来就得到一个正五角星，五角星是非常美丽的图形，中国的国旗上就有五颗，还有不少国家的国旗也用五角星，这是为什么？因为在五角星中可以找到的所有线段之间的长度关系都是符合黄金分割比的，如C点就是AB的黄金分割点。而且五角星里面的所有三角形都是黄金三角形。

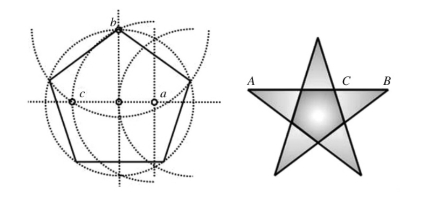
黄金分割线：直线L将一个面积为S的图形分成两部分，这两部分的面积分别为S1、S，如果S1∶S=S2∶S1，那么称直线L为该图形的黄金分割线。

世界万事万物充满了黄金分割比。

画家们发现，按0.618∶1来设计腿长与身高的比例，画出的人体身材最优美，如古希腊维纳斯女神塑像及太阳神阿波罗的形象等双腿与身高的比值均为0.618，从而创造了艺术美。

音乐家还发现，二胡演奏中，“千金”分弦的比符合0.618∶1时，奏出来的音调最和谐、最悦耳。

在建筑艺术中，黄金分割被认为是建筑和艺术中最理想的比例。建筑师们对数字0.618特别偏爱，无论是古埃及的金字塔，还是巴黎的圣母院，或者是近世纪的法国埃菲尔铁塔，都有与0.618有关的数据。0.618，被认为是建筑和艺术中最理想的比例。

地球表面的纬度范围是0°～90°，对其进行黄金分割，则34.38°～55.62°正是地球的黄金地带。无论从平均气温、年日照时数、年降水量、相对湿度等方面都是具备适于人类生活的最佳地区。说来也巧，这一地区几乎囊括了世界上所有的发达国家，如美国、加拿大、英国、法国、德国、日本、韩国等。

人体美学中，黄金分割与人的关系也相当密切。只有整体的和谐、比例的协调，才能称得上是一种完整的美。

为什么人们对这样的比例，会本能地感到美的存在？其实这与人类的演化和人体正常发育密切相关。据研究，从猿到人的进化过程中，人体结构中有许多比例关系非常接近0.618，从而使人体美在几十万年的历史积淀中固定下来。人类最熟悉自己，势必将人体美作为最高的审美标准，凡是与人体相似的物体就喜欢它，就觉得美。于是黄金分割律作为一种重要形式美法则，成为世代相传的审美经典规律，至今不衰！

在研究黄金分割与人体关系时，人们发现了人体结构中有众多的“黄金分割点”“黄金矩形”和“黄金指数”（两物体间的比例关系为0.618）。

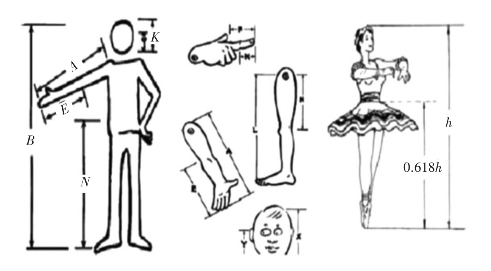
如人体中的黄金点有：

（1）肚脐：头顶—足底之分割点；

（2）咽喉：头顶—肚脐之分割点；

（3）膝关节：肚脐—足底之分割点；

（4）肘关节：肩关节—中指尖之分割点等。

黄金矩形有：

（1）躯体轮廓：肩宽与臀宽的平均数为宽，肩峰至臀底的高度为长；

（2）面部轮廓：眼水平线的面宽为宽，发际至颏底间距为长；

（3）鼻部轮廓：鼻翼为宽，鼻根至鼻底间距为长；

（4）唇部轮廓：静止状态时上下唇峰间距为宽，口角间距为长；等。

黄金指数有：

（1）反映鼻口关系的鼻唇指数：鼻翼宽与口角间距之比近似黄金数；

（2）反映眼口关系的目唇指数：口角间距与两眼外眦间距之比近似黄金数；

（3）0.618，作为一个人体健美的标准尺度之一，是无可非议的，但不能忽视其存在着“模糊特性”，它同其他美学参数一样，受种族、地域、个体差异的制约，都有一个允许变化的幅度。

医学与0.618也有着千丝万缕的联系，它可解释人为什么在环境22～24℃时感觉最舒适。因为人的体温为37℃，与0.618的乘积为22.8℃，而且这一温度中肌体的新陈代谢、生理节奏和生理功能均处于最佳状态。科学家们还发现，当外界环境温度为人体温度的0.618倍时，人会感到最舒服。

现代医学研究还表明，0.618与养生之道息息相关，动与静是一个0.618的比例关系，大致四分动六分静，才是最佳的养生之道。医学分析还发现，饭吃六七成饱的几乎不生胃病。

其他方面，如理想的体重大约是身高×（1－0.618）。

还有大家十分熟悉的苹果手机的商标，看似简单，却处处包含着黄金分割比。

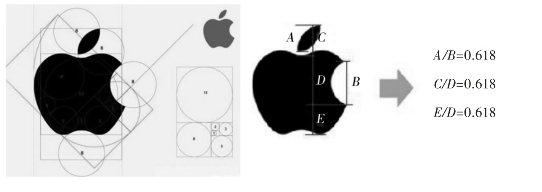
黄金数0.618更为数学家所关注，它的出现，不仅解决了许多数学难题（如：十等分、五等分圆周；求18度、36度角的正弦、余弦值等），而且还广泛应用于优选法中。

华罗庚与优选法：

优选法是以数学原理为指导，合理安排试验，以尽可能少的试验次数尽快找到生产和科学实验中最优方案的科学方法。

例如：在现代体育实践的科学实验中，运动员的饮食怎样选取最合适的配方、配比；产品制造如何寻找最好的操作方案和工艺条件；如何找出产品的最合理的设计参数，使产品的质量最好，产量最多，或在一定条件下成本最低，或消耗原料最少，生产周期最短等。把这种选取最合适的配方、配比，寻找最好的操作和工艺条件，给出产品最合理的设计参数，就叫做优选法，优选法也叫最优化方法。

优选法是一种具有广泛应用价值的求最优化问题的数学方法，著名数学家华罗庚曾为普及它作出过重要贡献。所谓优选法，就是华罗庚运用黄金分割法发明的一种可以尽可能减少做试验次数、尽快地找到最优方案的方法。

如在炼钢时需要加入某种化学元素来增加钢材的强度，这就有加入多少的问题，加多了不行，加少了也不行，只有完全合适才可以。假设已知在每吨钢中需加某化学元素的量在1000～2000克之间，为了求得最恰当的加入量，需要在1000克与2000克这个区间中进行试验。通常是取区间的中点（即1500克）做试验。然后将试验结果分别与1000克和2000克时的实验结果作比较，从中选取强度较高的两点作为新的区间，再取新区间的中点做试验，再比较端点，依次下去，直到取得最理想的结果。这种实验法称为对分法。但这种方法并不是最快的实验方法。如果将实验点取在区间的0.618处，即应用黄金分割法，那么实验的次数将大大减少。我们用一个有刻度的纸条来表示1000克至2000克，在纸条上找到1618（1000+1000×0.618）克的地点画一条竖线，做一次试验，然后把纸条对折起来，找到1618的对称点1382（1000+618×0.618），再做一次试验，如果1382克为最好，则把1618以外的纸条裁掉。然后再对折，找到1382的对称点1236（1000+382×0.618）做试验，这样循环往复，就可以找到最佳的数值。

这种取区间的0.618处作为试验点的方法就是一维的优选法，也称0.618法。

实践证明，对于一个相关的问题，用“0.618法”做16次试验就可以完成“对分法”做2500次试验所达到的效果。

又例如，在一种试验中，温度的变化范围是0~10℃，我们要寻找在哪个温度时实验效果最佳。为此，可以先找出温度变化范围的黄金分割点，考察10×0.618=6.18（℃）时的试验效果，再考察10×（1-0.618）=3.82（℃）时的试验效果，比较两者，选优去劣。然后在缩小的变化范围内继续这样寻找，直至选出最佳温度。

优选法在我国的应用，是从上个世纪60年代开始，首先由我国著名数学家华罗庚等推广并大量应用。经过20年左右的努力，产生了数以十亿计的巨大经济效益，被评为“全国重大科技成果奖”。

“优选法”中最典型的例子是华罗庚利用优选法成就了酒业龙头五粮液酒厂。

宜宾美酒五粮液之所以能够成为中国第一名酒，其中就有华罗庚优选法的功劳。

1972年，有外商提出，希望能销售五粮液低度酒。那时在国外低度酒还占主导地位，所以很多外国人对五粮液的高度数望而生畏。但国内不少人认为，五粮液好就好在高度，低度就要变味，就不是五粮液。五粮液的度数为什么就不能降低呢？当时五粮液负责科研技术工作的刘沛龙琢磨起了这个问题。顶着各方压力，刘沛龙整整搞了六年试验，但依然没有成功。低度酒不是多掺点水就行，这是一个对酒质的全新要求，尤其对于五粮液这样的名优白酒来说，要求就更为严格。但刘沛龙不甘放弃，不分白昼地钻进了自己摆的酒阵。直到1978年，华罗庚先生率领一个小分队来川推广优选法和统筹法，刘沛龙有幸参加了小分队在宜宾的活动，并听了多次讲学。刘沛龙如鱼得水，立即学以致用，以优选法来指导实验。当时的五粮液酒厂也十分重视这项工作，成立了双选办公室。

刘沛龙利用优选法，终于解开了酒阵之谜。在一个星期的时间里，用优选法选出了38度和35度这两个最佳度数，然后将两种酒放进冰箱，静观其变。成功了！他原来担心的致浊程度和析出物状态已达到预期效果。经过过滤处理后，手中的酒晶莹、碧透，像高度酒那么无色透明，口感很好，五粮液固有的风格特点并没有走样。尽管成功只用了六天功夫，但曾经摸爬滚打的六年却为他奠定了通向成功的基石。喜庆之余，刘沛龙装了两瓶38度和35度低度酒，送给华罗庚先生，并在酒瓶上题了两句表示感谢的话：“六年未成功，双法出成果。”华罗庚先生闻知此事也非常高兴，欣然题诗回赠：“名酒五粮液，优选味更醇；省粮五百担，产量增五成。豪饮李太白，雅酌陶渊明；深恨生太早，只能享老春。”后来刘沛龙又将38度改成39度，口感更醇净甘爽，在国际市场引起了不小震动，订货量猛增了3倍。国外对酒的税收额是随酒的度数增减来收的，度数高税收就越高，度数低税收也更低。因此这一项出口就为国家节约了大额酒税，创造了丰厚的经济效益。五粮液回归经典的老酒，重新启用上个世纪80年代的造型，从某种意义上来说，也可以看作是对华罗庚先生的一种纪念。

华老先生的优选法讲解通俗易懂，现摘片段供大家欣赏。

（1）请大家记好一个数字0.618。

（2）举例说：进行某工艺时，温度的最佳点可能在1000～2000℃之间。

当然，我们可以隔一度做一个试验，做完一千个试点之后，我们一定可以找到最佳温度，但要做一千次试验。

（3）（取出纸条）假定这是有刻度的纸条，刻了1000℃到2000℃。第一个试点在总长度的0.618处做，总长度是1000，乘以0.618是618，也就是说第一点在1618℃做，做出结果记下。

（4）把纸条对折，在第一试点的对面，即点②（1382℃）处做第二次试验。比较第一、二试点结果，在较差点（例如①）处将纸条撕下不要。

（5）对剩下的纸条，重复（4）的处理方法，直到找出最好点。

用这样的办法，普通工人一听就能懂，懂了就能用。

人们都知道，华罗庚是数论大家，研究的是数学上的高端问题。但在推广优选法上，华老把高深的数学问题简约化、通俗化、形象化了。他把优选法、统筹法形象化为淘米做饭、煮茶等日常事务中各道工序的合理排列，就连普通农妇都能听得懂。可以肯定地说，华罗庚先生面对上万名群众所作的绝对不是学术报告，他要真讲起优选法、统筹法、“0.618法”的数学原理和数学模型，估计没有几个人能听得懂。但他却让普通老百姓明白了一些在高深数学原理指导下的实际应用，他做了一次伟大的数学科普工作，受到了大众的热烈欢迎。华罗庚所到之处也是人山人海，用今天的话说，也可以叫“华罗庚热”。

所以，数学来源于实践，又应用到实践。数学不只是数学家的智力游戏，更是大众日常生活和生产的必要工具。