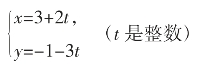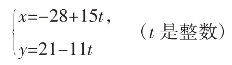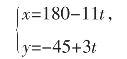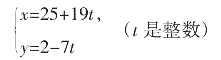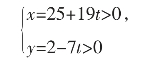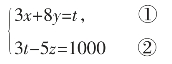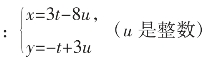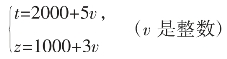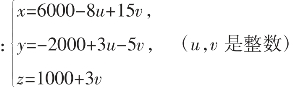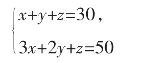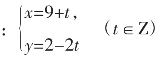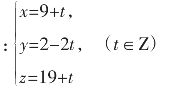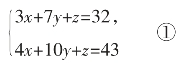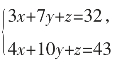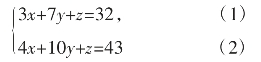百钱买百鸡与丢番图方程
“百鸡问题”是一道闻名于世界的古老题目,很有价值,也很有趣味。百鸡问题出自中国古代5~6世纪成书的《张邱建算经》,是原书卷下第38题,也是全书的最后一题。该问题是一个三元不定方程组,其重要之处在于开创“一问多答”的先例,这是过去中国古算书中所没有的。
具体问题是:“今有鸡翁一,值钱伍;鸡母一,值钱三;鸡雏三,值钱一。凡百钱买鸡百只,问鸡翁、母、雏各几何?”
用现代话说就是:“用100元钱买100只鸡,其中,公鸡一只5元钱,母鸡一只3元钱,小鸡三只1元钱。问买到的100只鸡中公鸡、母鸡、小鸡各是多少只?”
原书只给出了答案,没有给出具体解法。
书中又说如果少买7只母鸡,就可多买4只公鸡和3只小鸡。所以只要得出一组答案,就可以推出其余几组答案。
下面我们给出一种“逼近式”的推算方法:
因为公鸡一只5元钱,用100元钱买100只鸡,因此公鸡不能超过20只;同理母鸡不能超过33只;当然小鸡也不能超过100只。
我们先取一个中间数,假如公鸡买10只,用钱50元;母鸡买15只,用钱45元;还剩5元钱,只能买15只小鸡,鸡的总数才是40只,远远达不到100只。所以必须增加更多小鸡的数量,才能满足题目的需要。设想小鸡增加到60只,用钱20元,而剩下的40只如果全部买母鸡,也要用钱120元,而公鸡还要贵一点,所以远远超过了所需的100元,所以继续增加小鸡的数量,而小鸡的数量又必须是3的倍数。若小鸡增加到75只,用钱25元;而剩下的25只鸡如果全买母鸡,则用钱75元,刚好100元钱买了100只鸡。
如果按照书中给出的说法,少买7只母鸡,就可多买4只公鸡和3只小鸡。
其意思可作如下表示:
母鸡每减少7只:25→18→11→4;
则公鸡增加4只:0→4→8→12;
小鸡应增加3只:75→78→81→84。
因此就可以推出其他几组答案,所以卖鸡的方案共有以下4种:
公鸡0只,母鸡25只,小鸡75只;
公鸡4只,母鸡18只,小鸡78只;
公鸡8只,母鸡11只,小鸡81只;
公鸡12只,母鸡4只,小鸡84只。
《张邱建算经》中给出的答案是:“鸡翁四,值钱二十;鸡母十八,值钱五十四;鸡雏七十八,值钱二十六。又答:鸡翁八,值钱四十;鸡母十一,值钱三十三,鸡雏八十一,值钱二十七。又答:鸡翁十二,值钱六十;鸡母四、值钱十二;鸡雏八十四,值钱二十八。”
当然,第一种答案也是符合要求的。如果三种鸡都要有,则只取后三个答案。
“百鸡问题”提出以来,中国很多的古算书都没能给出具体解法,到了清代,研究百鸡术的人渐多,1815年骆腾风使用大衍求一术解决了百鸡问题。1874年丁取忠又创用一个简易的算术解法。在此前后时曰醇(约1870年)推广了百鸡问题,作《百鸡术衍》,从此百鸡问题和百鸡术才广为人知。
百鸡问题还有多种表达形式,如百僧吃百馒,百钱买百禽等。宋代杨辉算书内也有类似问题,印度算书和阿拉伯学者艾布·卡米勒的著作内都有百钱买百禽的问题,且与《张邱建算经》的题目几乎相同。
“百鸡问题”用现代数学观点来看,实际上是一个求三元不定方程整数解的问题。用列方程和解方程的方法可得其具体解法如下:
设公鸡、母鸡、小鸡分别为x、y、z只,由题意得:
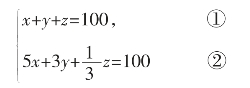
这里有两个方程,但是有三个未知量,这样的方程组称为不定方程组。
不定方程组有多种解,下面给出一种解法。
作②×3-①,整理得:7x+4y=100;
所以,y=(100-7x)/4=25-2x+x/4
令x/4=t,(t为整数)所以x=4t
把x=4t代入7x+4y=100得到:y=25-7t
易得z=75+3t,
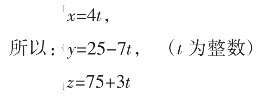
又因为x,y,z是非负整数,所以,
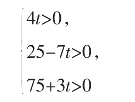
解得:0≤t≤3。
所以t=0,1,2,3。
当t=0时,x=0,y=25,z=75;
当t=1时,x=4,y=18,z=78;
当t=2时,x=8,y=11,z=81;
当t=3时,x=12,y=4,z=84。
则一百只鸡的搭配结果分别为:
公鸡0只,母鸡25只,小鸡75只;
公鸡4只,母鸡18只,小鸡78只;
公鸡8只,母鸡11只,小鸡81只;
公鸡12只,母鸡4只,小鸡84只。
还有人把“百鸡问题”编写成一首小诗如下:
百钱买来百只鸡,公母小鸡数不齐;
母一钱三公钱五,三雏钱一价格低。
公鸡母鸡各多少?还有几只是小鸡?
在《张丘建算经》以前的古算书上,从来没有出现过这种“一题三答”的题目。从这一点上看,“百鸡问题”是张丘建在数学上的伟大贡献。
公元15世纪,亚细亚的数学家阿尔·喀西所著《算术之钥》中,有一个“百钱买百鸟”的类似题目:
“今有鸭一值四钱,雀五值一钱,鸡一值一钱。凡百钱买百鸟,问鸭、雀、鸡各几何?”
这个问题显然与“百鸡问题”一致,但要比百鸡问题晚近10个世纪。
经推算,鸭、雀、鸡的数目符合题意的答案有如下五组:
①20,75,5;
②16,60,24;
③12,45,43;
④8,30,62;
⑤4,15,81。
由“百鸡问题”我们看到了不定方程,用方程的思想解这一类问题,程序清楚、解答简便,而且能很快得到符合条件的所有解。那么不定方程是如何定义的?它都有哪些条件和解法呢?
不定方程(indeterminate equation)是数论中最古老的一个分支,它有着悠久的历史与丰富的内容。所谓不定方程是指解的范围为整数、正整数、有理数或代数整数的方程或方程组,其未知数的个数通常多于方程的个数。
古希腊数学家丢番图于三世纪初就研究过若干这类方程,所以不定方程又称丢番图方程,是数论的重要分支学科,也是历史上最活跃的数学领域之一。不定方程的内容十分丰富,与代数数论、几何数论、集合数论等都有较为密切的联系。
丢番图(Diophantus,公元246—330),古代希腊人,是古希腊亚历山大学后期的重要学者和数学家,被誉为代数学的鼻祖。丢番图对算术理论有深入的研究,他完全脱离了几何形式,在希腊数学中独树一帜。今天我们称整系数的不定方程为“Diophantus方程”,其内容主要是探讨他们的整数解或有理数解。丢番图有三本著作,其中最有名的是《算术》,当中包含了189个问题及其答案,而许多问题都是不定方程或不定方程组(两个变数以上)问题。丢番图方程之所以被称为不定方程,是因为此类方程有时无解,有时多解,有时又有无穷多解。

丢番图
丢番图的出生日期不可靠,但他的墓碑上的墓志铭却是一道很经典的数学题目,流传甚广。
墓志铭上写着:“坟中安葬着丢番图,多么令人惊讶,它忠实地记录了所经历的道路。上帝给予的童年占六分之一,又过了十二分之一,两颊长胡,再过七分之一,点燃起结婚的蜡烛。五年之后天赐贵子,可怜迟来的宁馨儿,享年仅及其父之半,便进入冰冷的墓。悲伤只有用数论的研究去弥补,又过了四年,他也走完了人生的旅途。”
我们从中可以知道:“丢番图的一生,幼年占1/6,青少年占1/12,又过了1/7才结婚,5年后生子,子先父4年而卒,寿为其父之半。”那么,丢番图到底活了多少岁呢?
设丢番图活了x岁,计算丢番图年龄的方程为:
x/6+x/12+x/7+5+x/2+4=x,
解得x=84
由此知道丢番图享年84岁。
丢番图开始当爸爸的年龄:84×(1/6+1/12+1/7)+5=38(岁);
儿子死时丢番图的年龄:84-4=80(岁);
儿子活了42岁。
丢番图的墓志铭虽然只是一个简单的代数方程问题,但却是对这位代数之父的一种最好的纪念。
不定方程是一类实用且有趣的方程。研究不定方程需要解决三个问题:
(1)判定不定方程是否有解;
(2)判定不定方程的解的个数(有限个还是无限个);
(3)求不定方程的所有整数解。
中国是研究不定方程最早的国家,公元初的五家共井问题就是一个不定方程组问题,公元5世纪张丘建的百鸡问题标志中国对不定方程理论有了系统研究,秦九韶的大衍求一术又将不定方程与同余理论联系了起来。
我们先来看二元一次不定方程。
二元一次不定方程的一般形式为ax+by=c。
其中a,b,c是整数,ab≠0。
此方程有整数解的充分必要条件是a、b的最大公约数能整除c。
即,(a,b)│c。
若(a,b)=1,设x0、y0是该方程的一组整数解,那么该方程的所有整数解(通解)可表示为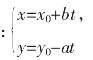 其中t是整数。
其中t是整数。
证明:因为x0、y0是该方程的一组整数解,则
ax0+by0=c
那么,a(x0+bt)+b(y0-at)=ax0+by0=c
所以 是原方程的解。
是原方程的解。
解二元一次不定方程通常先判定方程有无解。
若有解,可先求ax+by=c的一个特解,从而写出通解。
当不定方程系数不大时,有时可以通过观察法求得其解,系数较大时可引入变量,逐渐减小系数,直到容易得其特解为止。
例如,解二元一次不定方程3x+2y=7,
显然(3,-1)是该方程的一组解,那么,该方程的所有解可表示为:
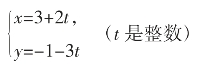
我们也可用“归一”的方法来求特解。
令3x+2y=1
观察其特解为(1,-1),
然后把特解扩大7倍,即可得原方程的特解是(7,-7),
所以原方程的通解也可表示为:

两个通解形式上不同,但本质上是一致的,在第二个通解中,令t=-2时,既是第一种解法的特解。如果令t=m-2,则第二个通解就与第一个通解完全等价。
可见,一般满足条件的二元一次不定方程在无约束条件的情况下,通常有无数组整数解,由于求出的特解不同,同一个不定方程的解的形式也可以不同,但它们所包含的全部解是一样的,将解中的参数t作适当代换,就可化为同一形式。
同理,三元一次不定方程的一般形式为:ax+by+cz=d,
a、b、c、d均为整数,且abc≠0。
此方程有整数解的充分必要条件是a,b,c的最大公约数整除d。
以此类推,即可得到多元一次不定方程的一般形式和有解的条件。
关于整数多元一次不定方程,也可以有矩阵解法、程序设计等相关方法辅助求解。
我们再来看二元二次不定方程。
二元二次不定方程本质上可以归结为求二次曲线(即圆锥曲线)的有理点或整点问题。
如二元二次方程:x2+y2=4,就是一个二元二次不定方程,它在解析几何中又是一个圆的方程,它的所有解所对应的点都在以原点为圆心、以2为半径的圆上。
比如整点就有(0,-2),(2,0),(0,2),(-2,0)。
又如二元二次方程:4x2+9y2=25,也是一个不定方程,它在解析几何中是一个椭圆的方程,它的所有解所对应的点都在以原点为中心的椭圆上。
整点有(-2,-1),(-2,1),(2,-1),(2,1)等。
有理点有(0,±5/3),(±5/2,0)等。
勾股定理也是一类特殊的二次不定方程,其表达式是:
x2+y2=z2
其正整数解通常称商高数或勾股数或毕达哥拉斯数。中国《周髀算经》中就有“勾广三,股修四,经隅五”之说,已经知道(3,4,5)是一个解。刘徽在注《九章算术》中又给出了(5,12,13),(8,15,17),(7,24,25),(20,21,29)几组勾股数。它的全部正整数解已在16世纪前得到。
即勾股数方程的全部正整数解(x,y的顺序不加区别)可表示为如下形式:x=k(m2-n2),y=2kmn,z=k(m2+n2),其中k,m,n均为正整数,且m>n。
另一类特殊的二次不定方程是所谓的佩尔方程:x2-Dy2=1,D是非平方的正整数。利用连分数理论知此方程永远有解。这类方程就是求双曲线上的有理点。
最后一类就是平方剩余问题,即求x2-py=q的整数解,用高斯的同余理论来描述,就是求x2≡q(mod p)的剩余类解。高斯发现的著名二次互反律给出了此方程是否有解的判定方法。这类方程就相当于求抛物线上的整点。
对高于二次的不定方程,情况相当复杂,仅举一例。
例:当n>2时,不定方程xn+yn=zn没有非平凡的整数解。
这即是著名的费马大定理。费马大约在1637年左右提出此定理,但从提出到证明,历经了3个多世纪,终于在1995年由英国数学家安德鲁·怀尔斯给出了完全证明。
m个n元一次不定方程组成的方程组,其中m<n,叫做线性不定方程组。
解此方程组,可以逐步消去m-1个未知数,从而消去了m-1个不定方程,将方程组转化为一个n-m+1元的一次不定方程,再来求解。
如百鸡问题,就是一个三元不定方程组,因为方程只有两个,可通过消去一个未知数,转化为一个二元一次不定方程来解就比较简单。
下面举一些简单例题来看其基本解法。
例1:求11x+15y=7的整数解。
解法1:将方程变形得11x+11y=7-4y
因为x、y是整数,所以7-4y应是11的倍数。由观察得y=-1,x=2是这个方程的一组整数解,所以方程的特解为x=2,y=-1。
此方程的通解可以表示为:

解法2:先考察11x+15y=1,这就是著名的“归一”思想,通过观察易得
11×(-4)+15×(3)=1,
两边同乘以7得11×(-4×7)+15×(3×7)=7
所以取x=-28,y=21,从而得到一组特解。
此方程的通解可以表示为:
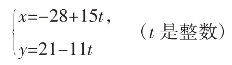
例2:求方程6x+22y=90的非负整数解。
解:因为(6,22)=2,所以方程两边同除以2,得
3x+11y=45 ①
可以先看方程,3x+11y=1,
由观察知,x=4,y=-1是方程3x+11y=1的一组整数解,从而方程①的一组整数解为
x=4×45=180
y=-1×45=-45
由此,可得方程①的一切整数解为:
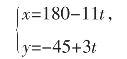
因为要求的是原方程的非负整数解,所以必有180-11t≥0且-45+3t≥0,
可得15≤t≤16.36,由于t是整数,所以只有t=15,t=16两种可能。
当t=15时,x=15,y=0;当t=16时,x=4,y=3.
所以原方程的非负整数解是:(15,0),(4,3)。
例3:求方程7x+19y=213的所有正整数解。
分析:这个方程的系数较大,用观察法去求其特殊解比较困难,碰到这种情况我们可用逐步缩小系数的方法使系数变小,最后再用观察法求得其解。
解:由方程
7x+19y=213 ①
用最小系数7除方程①的各项,并移项得
x=-2y-5y/7+30+3/7
因为x,y是整数,故(3-5y)/7=u也是整数,
于是方程可转化为5y+7u=3。②
由观察知y=2,u=-1是方程②的一组解。
将y=2代入①得x=25。
于是方程①有一组解x0=25,y0=2,所以它的一切解为
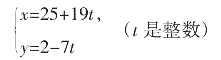
由于要求方程是正整数解,所以
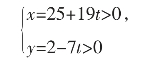
解不等式,得t只能取-1和0。
因此得原方程的正整数解只有(6,9),(25,2)。
例4:我国纸币有1元、5元、10元、20元、50元和100元6种,如果手头只有1元5张、5元15张、20元10张,现要用这3种纸币支付143元货款,有多少种不同的支付方法?
解:显然个位数的3元只能用1元来支付,剩下的140元也只能用5元和20元2种纸币来支付。
设5元需要x张,20元需要y张,恰好支付140元,于是
5x+20y=140
即 x+4y=28 ①
只需求①的非负整数解即可。
由于4y≤28,所以y≤7,所以,y=0,1,2,3,4,5,6,7。
从而x=28,24,20,16,12,8,4,0。
所以①的非负整数解有8组。因5元的纸币只有15张,所以,共有4种不同的支付方式,它们分别是:
(1元,5元,20元)→
(3张,0张,7张)、(3张,4张,6张)、(3张,8张,5张)、(3张,12张,4张)。
多元一次不定方程可以化为二元一次不定方程来解。
例5:求方程9x+24y-5z=1000的整数解。
解:设9x+24y=3t,即3x+8y=t,代入原方程,得:3t-5z=1000。
于是原方程可化为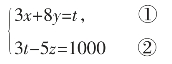
用前面的方法可以求得①的解为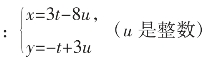
②的解为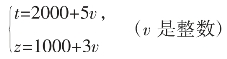
消去t,得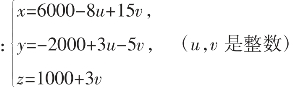
这就是三元不定方程的通解。
下面我们来看古老的“五家共井”问题。
“五家共井”问题和“百鸡问题”一样,都是一个著名的问题。
“五家共井”问题是古代数学巨著《九章算术》中的一道题目。内容是:“五家共井,甲二绠(汲水用的井绳)不足,如(接上)乙一绠;乙三绠不足,如丙一绠;丙四绠不足,如丁一绠;丁五绠不足,如戊一绠;戊六绠不足,如甲一绠,皆及。”
意思就是说5家人共用一口井,甲家的绳子用2条不够,还要再用乙家的绳子1条才能打到井水;乙家的绳子用3条不够,还要再用丙家的绳子1条才能打到井水;丙家的绳子用4条不够,还要再用丁家的绳子1条才能打到井水;丁家的绳子用5条不够,还要再用戊家的绳子1条才能打到井水;戊家的绳子用6条不够,还要再用甲家的绳子1条才能打到井水。
最后问:井有多深?每家的绳子各有多长?
分析:同样这也是属于不定方程。
我们设井深为h,各家的绳长分别为a,b,c,d,e,
则可以列出如下方程组:
2a+b=h①
3b+c=h②
4c+d=h③
5d+e=h④
6e+a=h⑤
这个题目列的是六元一次不定方程组,
解方程组得a、b、c、d、e分别等于:
265、191、148、129、76,而井深为721 m。
所以,井深721 m,甲绳长265 m,乙绳长191 m,丙绳长148 m,丁绳长129 m,戊绳长76 m。
马克思解不定方程。马克思作为伟大的无产阶级革命家和导师,又是一位伟大的思想家和哲学家,其《资本论》《共产党宣言》等著作均是世界级经典。马克思为了写好《资本论》,深入钻研数学知识,在数学领域有很多独到的见解,还编写出版了《数学手稿》,是用辩证唯物主义思想研究数学的典范。书中也涉及了不定方程问题,其中有这样一道题目:
“有30个人,其中有男人、女人和小孩,在一家小饭馆里花了50先令,每个男人花3先令,每个女人花2先令,每个小孩花1先令,问男人、女人和小孩各有多少人?”
解:设男人、女人和小孩分别有x、y、z个人,则
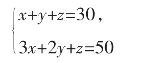
化简得:2x+y=20
其一个特解为(9,2)
可得通解为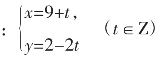
原方程组的通解为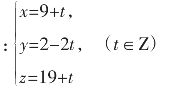
由于x,y,z为正整数,所以,-9<t<1。
本题有9组解(x,y,z),它们分别是(1,18,11),(2,16,12),(3,14,13),(4,12,14),(5,10,15),(6,8,16),(7,6,17),(8,4,18),(9,2,19)。
最后来看一道公务员考试题。
题目:甲买了3支签字笔,7支圆珠笔和1支铅笔,共花了32元,乙买了4支同样的签字笔,10支圆珠笔和1支铅笔,共花了43元。如果同样的签字笔、圆珠笔、铅笔各买一支,共用多少钱?
A.10元;B.11元;C.17元;D.21元。
解法1:整体替换法
解析:根据题目,设购买签字笔、圆珠笔、铅笔分别为x元、y元、z元。
根据题意,可得: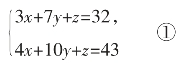
因为题目要求各买一支共用多少钱,即求x+y+z=?
所以就把x+y+z看成一个整体,由方程组①可得,
x+y+z+2(x+3y)=32
x+y+z+3(x+3y)=43
把x+y+z和x+3y看成一个整体,分别设为M,N,则
M+2N=32
M+3N=43
这样,三元不定方程组,就变成二元一次方程组。
解得M=10,即x+y+z=10,选A项。
解法2:奇偶特性法
(1)任意两个数的和如果是奇数,那么差也是奇数;如果和是偶数,那么差也是偶数。
(2)任意两个数的和或差是奇数,则两数奇偶相反;和或差是偶数,则两数奇偶相同。
解析:在4x+10y+z=43中,43是奇数,4x是偶数,10y是偶数,则z一定是奇数。
其次,在3x+7y+z=32中,32是偶数,z是奇数,则3x+7y一定是奇数,则x和y中,一定是一个偶数和一个奇数相加,所以,x+y+z中,是一个偶数,一个奇数和一个奇数相加,则和为偶数,选A项。
解法3:设0法
解析:根据题意,可列方程,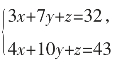
这是三元不定方程,不能单独求出x,y,z。但是若能变成二元方程组,则可以单独把未知数求出。因此,对于本题目可以设其中的一个未知数为0,就相当于买两种笔,送了一种笔。一般设系数比较大的未知数为0,这样便于计算,因此,设y=0,当然也可以设x或z为0都可以。
则可得,3x+z=32
4x+z=43
解得,x=11,z=-1,则,x+y+z=11+0+(-1)=10,选A项。
解法4:拼凑法
这种方法,一般是两个方程相加或相减之后,再进行拼凑。
根据题意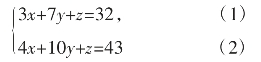
(2)-(1)得:x+3y=11,则3x+9x=33(3)
(2)-(3)得:x+y+z=10,所以选(A)。
不定方程是现实生活中非常常见的一类问题,古人的研究给我们带来了很多至今都很有效的方法,如代入法、消元法、代换法、奇偶特性法、尾数法等。这些方法不仅可以应用在解决不定方程问题上,而且在数学运算的其他问题上也有着广泛的应用。
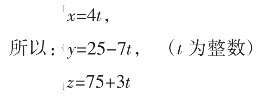
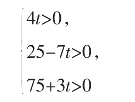

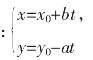 其中t是整数。
其中t是整数。 是原方程的解。
是原方程的解。