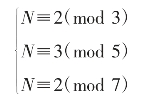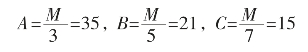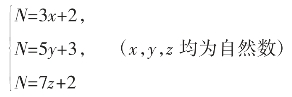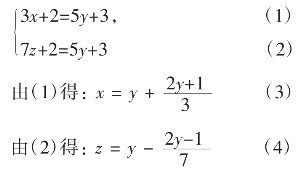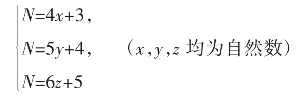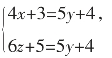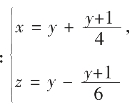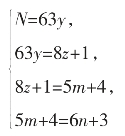韩信将兵与中国剩余定理
江苏淮安流传着一则民间故事——“韩信将兵”，后来故事逐渐演绎成一句成语“韩信将兵，多多益善”，被人们所熟知。
韩信（约公元前231年—前196年），淮阴（原江苏省淮阴县，今淮安市淮阴区）人，西汉开国功臣，中国历史上杰出的军事家，汉初三杰之一，兵家四圣之一，同时也是中国军事思想“兵权谋家”的代表人物，被后人奉为“兵仙”“神帅”等。
秦朝末年，楚汉相争。汉王刘邦在丞相萧何的极力推荐下，拜韩信为大将军。韩信足智多谋，善于带兵，为刘邦汉朝的建立立下了汗马功劳。一次，刘邦问韩信：“你觉得我可以带多少兵？”，韩信答：“最多能带十万”，刘邦不解地问：“那你呢？”韩信自豪地说：“越多越好，多多益善嘛！”刘邦半开玩笑半认真地说：“那我不是打不过你？”韩信说：“不，主公是驾驭将军的人才，不是驾驭士兵的，而将军们是专门训练士兵的。”刘邦转怒为乐。
韩信作为统帅，他擒魏、取代、破赵、胁燕、东击齐，南灭楚垓下，名闻海内，威震天下。作为军事理论家，他与张良整理兵书，并著有《韩信》兵法三篇。刘邦曾说：运筹策帷帐之中，决胜於千里之外，吾不如子房。镇国家，抚百姓，吾不如萧何。连百万之军，战必胜，攻必取，吾不如韩信。此三者，皆人杰也，吾能用之，此吾所以取天下也。韩信熟谙兵法，自言用兵“多多益善”，作为战术家韩信为后世留下了大量的战术典故：如明修栈道、暗度陈仓，四面楚歌，十面埋伏等。作为军事家，韩信是继孙武、白起之后，最为卓越的将领，是中国战争史上最善于灵活用兵的将领。
一次，韩信带1500名勇士与楚军交战，首战死有四五百人，为了再战，韩信快速地清点了人数，他要求3人一排站队，结果多出2人；5人一排站队，多出3人；7人一排站队，又多出2人，韩信马上宣布，我军有1073名勇士。汉军本来就信服自己的统帅，这一来更相信韩信是“神仙下凡”“神机妙算”。于是士气大振，一鼓作气，击败楚军。
韩信将兵的数字不一定真实，但韩信将兵的原理却出自我国古代数学名著《孙子算经》。
在一千多年前的《孙子算经》里，有一道著名的问题，叫“物不知其数”，其问题是：
“今有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二，问物几何？”
这也是一道驰名中外的古题。
按照今天的话来说就是：一个数除以3余2，除以5余3，除以7余2，求这个数（实际上是求其最小值）。
书中说，答曰：二十三。
这个问题非常典型，它虽然从简单的数物计数开始，却广泛应用于天文、历法、军事、工程之中，引起了后世极大的兴趣，开创了世界“同余式”研究的先河。它不是一个单个的问题，而是形成了一类问题。可以把这个问题看成是一个不定方程问题，也可以看成是初等数论中的解同余式问题，如果不限制，答案有无穷多组。
为了寻求解决这个问题的一般规律，古代数学家们认为“求一”是难点和关键所在。
在《孙子算经》中，聪明的古人不但提供了答案，而且还给出了一种简单的、有规律的解法。其关键步骤的表述是：
“凡三三数之剩一，则置七十；五五数之剩一，则置二十一；七七数之剩一，则置十五；一百六以上，以一百五减之既得。”
古文的意思是说，要找“被3除余2，并且是5和7的倍数”的数，首先要找“被3除余1，并且是5和7的倍数”，所以这个数最小就是70，即“三三数之剩一，则置七十”；
同样，要找“被5除余3，并且是3和7的倍数”的数，也要先找“被5除余1，并且是3和7的倍数”，这个数是21；
同理，要找“被7除余2，并且是3和5的倍数”的数，也要先找“被7除余1，并且是3和5的倍数”，这个数是15；
也就是说，“被3除余1，并且是5和7的倍数”，则取的第一个数就是70；
“被5除余1，并且是3和7的倍数”，则取的数就是21；
“被7除余1，并且是3和5的倍数”，则取的数就是15。
故物不知其数里，一个数除以3余2，应该取2个70；除以5余3，应该取3个21；除以7余2，应该取2个15。
然后把他们加起来如果比106大，就减去3，5，7的最小公倍数105，这样不影响余数的要求，最后求出的得数就是符合要求的最小的一个数。
故设所求的数为N，列出式子为：
N=70×2+21×3+15×2-2×105=23
所以，满足条件的数是23。
古人同时也把此算法编成了歌诀：
“三人同行七十稀，五树梅花廿一枝，七子团圆整半月，除百零五便得知。”
其解题规律与前面相同，具体步骤也就是：
三人同行七十稀——被3除余1，并且是5和7的倍数，此数是70；
五树梅花廿一枝——被5除余1，并且是3和7的倍数，此数是21；
七子团圆整半月——被7除余1，并且是5和3的倍数，此数是15；
除百零五便得知——减去3、5和7的最小公倍数105（或105的倍数）便得知。
此方法具有一般性，现再举两例，体会一下古人的神奇妙算。
例1：有一个数，除以3余2，除以5余4，除以7余3，问这个数的最小值除以12余几？
解：由上面的算法可直接套用公式得：
N=70×2+21×4+15×3-2×105=59
显然，59除以12余11。
例2：一个数，除以5余3，除以7余4，除以9余3，问这个数的最小值是多少？
分析：我们可用上面的算法步骤进行。
要找“被5除余3，并且是7和9的倍数”的数，就要首先找“被5除余1，并且是7和9的倍数”的数，这个数是2×63=126；
同样，要找“被7除余4，并且是5和9的倍数”的数，也要先找“被7除余1，并且是5和9的倍数”的数，这个数是5×45=225；
同理，被9除余1，并且是5和7的倍数，这个数就是8×35=280。
又5，7，9这3个数的最小公倍数是5×7×9=315
故所求的数N为：
N=3×126+4×225+3×280-6×315=228
所以，满足条件的最小数是228。
此种算法，也被古人冠以很多神奇的名字：“孙子算法”“鬼谷算”“隔墙算”“秦王暗点兵”“韩信将兵”等。
我国古代数学具有构造性和机械化的特点，并且“寓理于算，不证自明”，这正是启迪智慧、训练思维的好平台。
现在让我们回到前面提到的韩信将兵问题，一千余人的军队，要求3人站一排结果多2人，5人一排多3人，7人一排又多2人，韩信马上宣布，我军有1073人，那韩将军是如何快速计算的呢？
由上面的算法可知，符合条件的最小数是23，其3，5，7的最小公倍数是105，则一千余人的军队可通过下面的算式很快得到：
105×10+23=1073（人）
所以，韩信便能很快得到士兵的总人数为1073人。
韩信将兵的例子很多，相传有一次汉高祖刘邦指着近万人的一支部队问大将军韩信，你能知道这队兵士的人数是多少吗？韩信立即组织士兵站队，每5人一列、9人一列、13人一列、17人一列结果都剩3人，韩信马上报告刘邦，士兵有9948人，刘邦茫然而不知其理。
首先，我们先求5，9，13，17的最小公倍数，因为5，9，13，17为两两互质的整数，故其最小公倍数为这些数的积9945，然后再加3，得9948人。
当然，对于“物不知其数”数字不大时，我们也可以采用通用的方法：“逐步满足法”，找出满足要求的数：
解：先列出除以3余2的数：2，5，8，11，14，17，20，23，26，…
再列出除以5余3的数：3，8，13，18，23，28，…
再列出除以7余2的数：2，9，16，23，30，…
找出第一个公共数，就得出符合题目条件的最小数是23。
孙子的算法具有一般性，很多同类问题都可以仿照此方法来解决。
我们再来看我国古代数学家杨辉的《续古摘奇算法》中的一道题目：
“七数剩一，八数剩二，九数剩三，问本总数几何？”
答曰：四百九十八。
术曰：七余一，下二百八十八，题内余一，下二百八十八；八余一，下四百四十一，题内余二，下八百八十二；九余一，下二百八十，题内余三，下八百四十。并之，二千一十，满五百四去之，去三个五百四，余四百九十八，合问。
我们通过列表来分析杨辉给出的算法：
列出算式为：
1×（4×8×9）+2×（7×7×9）+3×（5×7×8）-3×（7×8×9）=498
即符合条件的最小的数是498。
杨辉的算法与孙子的算法完全一致，由此可得出解这一类问题的一般规律。
“物不知其数”也是研究同余方程的重要来源。若用现代数论符号表示，可等价于解下列的一次同余组。
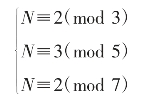
《孙子算经》所提供的方法本质上也是解一次同余式的一般方法，解题的关键在于求乘律，也就是解3个（余数是1）独立的同余式：
5×7×a≡1（mod 3）
3×7×b≡1（mod 5）
3×5×c≡1（mod 7）
求得最小的a=2，b=1，c=1
设M=[3，5，7]=3×5×7=105，
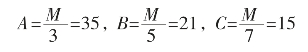
则N=2×aA+3×bB+2×cC-kM（k是正整数，k的取值使N为最小正整数。）
N=2×70+3×21+2×15-2×105=23
但是《孙子算经》的算法还是具有一定的特殊性和局限性。
宋朝著名的数学家秦九韶在其著作《数书九章》中，进一步完善了对一次同余式理论的研究工作，把“物不知其数”问题推广，得到了更一般的解法，并把该解法称之为“大衍求一术”。这一方法，被看作是中国数学史上最有创造性的成就之一，是中世纪数学的最高成就，比西方1801年著名数学家高斯建立的同余理论早554年，在当时就处于世界领先地位。秦九韶的“大衍求一术”还被德国著名数学家康托尔称之为“最幸运的天才”。这个解法传到西方后，被称为“孙子定理”或“中国剩余定理”。
中国剩余定理，亦即秦九韶的“大衍求一术”，就是中国古代求解一次同余式方程组问题的重要方法。
用现代数学的语言来说明的话，中国剩余定理就是给出了以下的一次线性同余方程组有解的条件和解法：
设m1，m2，…，mn是n个两两互质的正整数（条件），M=m1m2…mn，
的解是x≡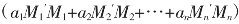
（mod M）
其中，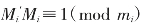
，i=1，2，…，n
这就是用构造法给出的一次同余式组在有解情况下解的具体形式。
解题过程也可通过列表来直观表示：
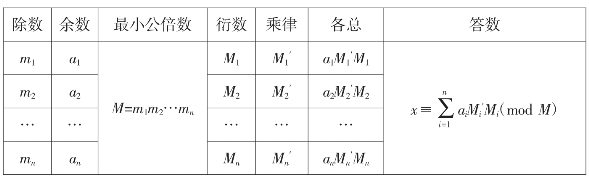
这就是“中国剩余定理”。
中国当代数学家陈景润在其著作《初等数论》中也给过一个类似“韩信将兵”的题目。
题目是：有兵一队，若列成五行纵队，末行一人；成六行纵队，则末行五人；成七行纵队，则末行四人；成十一行纵队，则末行十人，求兵数。
本题也就是说：有一个数被5除余1，被6除余5，被7除余4，被11除余10，求这个数。
现在就可以用“孙子定理”来解，列表如下：
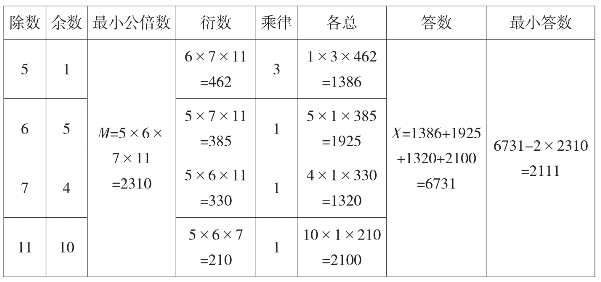
故所求的兵数至少是2111人。
当然，“物不知其数”，也可以看作是不定方程问题，此问题相当于求不定方程组
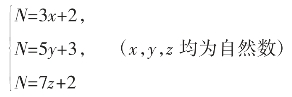
的正整数解N。
解：原方程组等价于
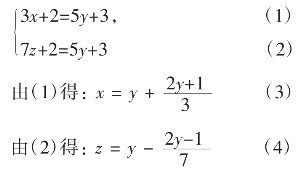
由于x，y，z均为自然数，所以，
由（3）可知：y只能取1，4，7，10，…（等差数列）；
由（4）可知：y只能取4，11，18，…
满足方程组的y最小只能取4，进而得知N=23。
进一步，y取的第二个数是25，可得N=128。
下面来看一些特殊的例子和特殊的方法。
例3：有一个数被4除余3，被5除余4，被6除余5，求这个数的最小值。
分析：由于4，5，6不能两两互质，所以此题的条件不符合“孙子定理”的条件，因此就不能用“孙子定理”来解。
这类问题我们可以考虑用不定方程来解。
解：设所求的数是N，则
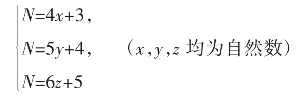
化简得：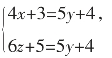
整理得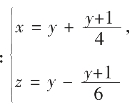
所以，求得y的最小值是11，故所求的最小值N是59。
例4：一筐鸡蛋，1个1个拿，正好拿完；2个2个拿，还剩1个；3个3个拿，正好拿完；4个4个拿，还剩1个；5个5个拿，还差1个；6个6个拿，还剩3个；7个7个拿，正好拿完；8个8个拿，还剩1个；9个9个拿，正好拿完。问筐里最少有多少个鸡蛋？
解：由已知，所求的数一定是一个奇数，而且是3，7，9的倍数，而3，7，9的最小公倍数是63。又4个4个拿剩1个与8个8个拿剩1个可以合并为后者，故可列出不定方程组为：
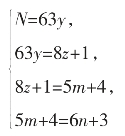
解这个方程组，可得最小的数是1449。
例5：一个数除以5余1，除以3也余1。问这个数最小是多少？（1除外）
特殊的方法：最小公倍数法。
除以5余1：说明这个数减去1后是5的倍数。
除以3余1：说明这个数减去1后也是3的倍数。
所以，这个数减去1后是3和5的公倍数。
要求最小，所以这个数减去1后就是3和5的最小公倍数15。
所以这个数是15+1=16。例1也可用此法解决。
例6：一个数被5除余2，被6除少2，被7除少3，这个数最小是多少？
题目可以看成，被5除余2，被6除余4，被7除余4。
分析：我们可以采用“同余合并法”。
题目中“被6除余4，被7除余4”，其余数相同，只要求出6和7的最小公倍数，再加上4，就是满足后面条件的数了，6×7+4=46。
下面一步试下46能不能满足第一个条件“一个数被5除余2”。不行的话，只要再在46后加上6和7的最小公倍数42，一直加到能满足“一个数被5除余2”即可。设所求数为：
N=46+42k，k=1，2，3，…
当k=3时，46+3×42=172符合条件。
由此可知，满足条件的数是172。
例7：有1个数，除以7余2，除以8余4，除以9余3，这个数至少是多少？
我们可以采用“余数分析法”。
比如除以7余2的数可以写成7n+2。
7n+2这样的数除以8余4，所以要求7n除以8余2。7n除以8余2，7除以8余7，要求n除以8余6（乘数之余等于余数之乘），则n最小取6。
所以满足“除以7余2，除以8余4”的最小的数是7×6+2=44，
则所有满足“除以7余2，除以8余4”的数都可以写成44+56m。
要求44+56m除以9余3，由于44除以9余8，所以要求56m除以9余4。（加数之余等于余数之加）
56m除以9余4，由于56除以9余2，所以要求m除以9余2（乘数之余等于余数之乘），则m最小取2。
所以满足“除以7余2，除以8余4，除以9余3”的最小的数是
44+56×2=156。
显然，以上算法都具有一定的特殊性和局限性。
小词典：
秦九韶（1208—1261），生于普州安岳（今四川省安岳县）。南宋著名数学家，与李冶、杨辉、朱世杰并称宋元数学四大家。秦九韶精研星象、音律、算术、诗词、弓箭、营造之学。秦九韶潜心研究数学多年，1247年完成数学巨著《数书九章》，其中的大衍求一术、三斜求积术和秦九韶算法（高次方程正根的数值求法）是有世界意义的重要贡献。这是一本划时代的巨著，该书内容丰富至极，上至天文、星象、历律、测候，下至河道、水利、建筑、运输，各种几何图形和体积，钱谷、赋役、市场、牙厘的计算和互易。许多计算方法和经验常数直到现在仍有很高的参考价值和实践意义，被誉为“算中宝典”，是中国数学史、乃至世界数学史上光彩夺目的一页，对后世数学发展产生了广泛的影响。我国数学史家梁宗巨评价道：“秦九韶的《数书九章》是一部划时代的巨著，内容丰富，精湛绝伦。特别是大衍求一术及高次代数方程的数值解法，在世界数学史上占有崇高的地位。”美国著名科学史家萨顿（G.Sarton，1884—1956）也说过，秦九韶是“他那个民族，他那个时代，并且确实也是那个时代最伟大的数学家之一”。