算术基本定理与辗转相除法

自然数是人类祖先在认识自然中所形成的最基本的数字，也是当今所掌握的数集中最小的数集。其中的加、减、乘、除运算也被称为算术运算，也是最基本、最重要的运算。但是在自然数集里，数和数之间或者一个数本身却有着千变万化的关系，可以说是魅力无穷、神秘莫测。如“完全数”“亲和数”“梅森素数”“哥德巴赫猜想”等就是其中最有名的例子，这些问题的很多方面至今还没有最终结果。

本节将对自然数中最基本、最常见、最实用的一些基本关系做一些介绍。如整除、倍数、约数、“算术基本定理”、辗转相除法或欧几里得算法等就是其中最基本、最重要的几种关系和算法。

1.倍数的相关概念

（1）倍数：一个整数能够被另一整数整除，那么这个整数就是另一个整数的倍数。如15能够被3或5整除，因此15是3的倍数，也是5的倍数。

或者，如果a、b、c是整数，而且满足：a÷b=c，就说a是b的倍数，同时a也是c的倍数；或者说a能被b（c）整除；或者说b（c）整除a。

一个数的倍数有无数个，也就是说一个数的倍数的集合为无限集。如果a是b的倍数，则ka也是b的倍数（k是非零整数）。如，3的倍数就有6，9，12，15，18，…

注意：不能把一个数单独叫做倍数，倍数是两个数之间的关系，只能说谁是谁的倍数。

（2）公倍数：两个或多个整数公有的倍数叫做它们的公倍数。如60就是5和6的公倍数。

（3）最小公倍数：两个或多个整数的公倍数里最小的那一个叫做它们的最小公倍数。如30就是5和6的最小公倍数，24就是6和8的最小公倍数。

（4）一些特殊的倍数关系：

2的倍数：一个数的个位数是偶数（如0，2，4，6，8），这个数就是2的倍数。如530，326，738等。

3的倍数：一个数的各个位上的数字之和是3的倍数，这个数就是3的倍数。如4926，（4+9+2+6）=21，是3的倍数，所以4926是3的倍数，且4926÷3=1642。

4的倍数：一个数的末两位数是4的倍数，这个数就是4的倍数。如2356，末两位数是56，而56÷4=14，是4的倍数。所以，2356是4的倍数，且2356÷4=589。

5的倍数：一个数的末尾数是0或5，这个数就是5的倍数。如7775，7775的末尾为5，所以7775是5的倍数，且7775÷5=1555。

6的倍数：一个数只要能同时被2和3整除，那么这个数就是6的倍数。如5364，既能被2整除，又能被3整除，所以5364是6的倍数。

7的倍数：若一个整数的个位数字截去，再从余下的数中，减去个位数的2倍，如果差是7的倍数，则原数能被7整除。如果差太大或心算不易看出是否是7的倍数，就重复上述“截尾、2倍、相减、验差”的过程，直到能清楚判断为止。例如，判断133是否是7的倍数的过程如下：13－3×2=7，所以133是7的倍数；又例如判断6139是否是7的倍数：613－9×2=595，59－5×2=49，49是7的倍数，所以6139是7的倍数。

8的倍数：一个数的末三位是8的倍数，这个数就是8的倍数。如7256，256÷8=32，32是8的倍数，所以7256是8的倍数，7256÷8=907。

9的倍数：若一个整数的各位数字之和能被9整除，则这个整数能被9整除。如376452，由于3+7+6+4+5+2=27是9的倍数，所以376452是9的倍数。

11的倍数：

①若一个整数的奇位数字之和与偶位数字之和的差能被11整除，则这个数能被11整除。如64834，奇位数字之和是6+8+4=18，偶位数字之和是4+3=7，它们的差是18-7=11，故64834是11的倍数，64834÷11=5894。

②11的倍数检验法也可用上述检验7的“割尾法”处理，过程唯一不同的是倍数不是2而是1。如2893，289-3=286，28-6=22，22是11的倍数，所以2893是11的倍数，2893÷11=263。

③将一个数从个位开始两两分隔，若所有分隔开的数相加为11的倍数，则这个数为11的倍数。如32571，分隔成3/25/71，3+25+71=99，99为11倍数，所以32571是11的倍数。

13的倍数：若一个整数的个位数字截去，再从余下的数中，加上个位数的4倍，如果和是13的倍数，则原数能被13整除。如果差太大或心算不易看出是否是13的倍数，就需要上述“截尾、4倍大、相加”的过程，直到能清楚判断为止。如77506，因为7750+6×4=7774，777+16=793，79+12=91，9+4=13，所以77506是13的倍数，77506÷13=5962。

将一个整数从个位开始三三分隔，若奇位数之和与偶位数之和的差能被7、11、13整除，则这个数能被7、11、13整除。如6139，分割6/139，做差139-6=133，133÷7=19，所以6139能被7整除；又如64834，分割64/834，做差834-64=770，而770是7和11的倍数，所以64834是7和11的倍数；又如77506，分割77/506，做差506-77=429，而429=13×11×3，由于429是11和13的倍数，所以77506是11和13的倍数。又例如385385，一定是7、11和13的倍数。

17的倍数：若一个整数的个位数字截去，再从余下的数中，减去个位数的5倍，如果差是17的倍数，则原数能被17整除。如果差太大或心算不易看出是否是17的倍数，继续前面的操作，直到能够判断为止。如31824，因为3182-4×5=3162，316-10=306，306=17×18（或30-5×6=0，0是17的倍数），由于306是17的倍数，所以31824是17的倍数，31824=17×1872。

25的倍数：两位数以上（不包含两位数），只要末两位是25的倍数，整个数就是25的倍数。

125的倍数：三位数以上（不包含三位数），只要后三位是125的倍数即可。

掌握一些常用数的倍数，一些大一点数的倍数也就掌握了。如48的倍数，就是既能被6又能被8整除的数等。

我们来看倍数的一个特殊性质：

任意两个奇数的平方差一定是8的倍数。

证明：设任意两个奇数为2n+1，2m+1，（m，n∈N）

（2m+1）2-（2n+1）2=（2m+1+2n+1）×（2m-2n）

=4（m+n+1）（m-n）

当m，n都是奇数或都是偶数时，m-n是偶数，能被2整除；

当m，n一奇一偶时，m+n+1是偶数，能被2整除；

所以（m+n+1）（m-n）一定是2的倍数，

则4（m+n+1）（m-n）一定是8的倍数。

下面来看如何求两个数的最小公倍数。

给出两个数：72，420，求它们的最小公倍数。

方法一：用短除法求最小公倍数。

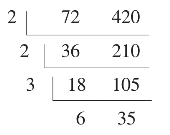
所求的最小公倍数为2×2×3×6×35=2520，2520=35×72=6×420。

方法二：分解质因数法。

72=23×32，420=22×3×5×7

取两个数的所有质因数，每个质因数选取次数最高的，然后相乘即得最小公倍数。即

23×32×5×7=2520就是所求的最小公倍数。

2.与约数相关的问题

（1）约数，又称因数。整数a除以整数b（b≠0），所得的商正好是整数而没有余数，我们就说a能被b整除，或b能整除a。a称为b的倍数，b称为a的约数。这里“约数”一词一般只限于正约数。约数和倍数都是二元关系的概念，不能孤立地说某个整数是约数或倍数。

一个整数的约数是有限的。同时，它可以在特定情况下成为公约数。

在自然数（0和正整数）的范围内，任何正整数都是0的约数。

4的正约数有：1，2，4。

6的正约数有：1，2，3，6。

10的正约数有：1，2，5，10。

12的正约数有：1，2，3，4，6，12。

15的正约数有：1，3，5，15。

18的正约数有：1，2，3，6，9，18。

注意：一个数的约数必然包括1及其本身。

那么，一个正整数到底有多少个约数，有无计算公式呢？答案是肯定的。

我们先来看一个在分解质因数的过程中的重要的基本定理：

（2）算术基本定理：任何一个大于1的整数总可以写成若干个质因数的乘积。如果不考虑质因数排列的前后次序，这种写法是唯一的，即：

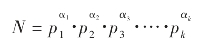
这里k是大于或等于1的整数，p1，p2，p3，…，pk是彼此不同的质数；α1，α2，α3，…，αk为大于或等于1的整数，且分别叫做p1，p2，p3，…，pk的指数。上式也叫做整数N的标准分解式。

此定理最早的证明由欧几里得给出。

如：360=23×32×5，10500=22×3×53×7等。

依据整数的标准分解式，通过推理归纳和乘法原理，我们可以求得这个整数的约数的个数。

（3）约数个数的计算公式：

设N是正整数，由标准分解式可知，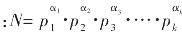

则形如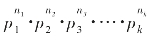的数都是n的约数，其中只含质数p1的指数n1可取：0，1，2，…，α1个值，有α1+1种取法；只含p2的n2可取α2+1个值；……；只含pk的nk可取αk+1个值；根据乘法原理，N的正约数共有σ

0（N）=（α1+1）（α2+1）（α3+1）…（αk+1）个。

上式即为求一个正整数约数个数的公式。

例如：360=23×32×5，

所以360的约数个数为（3+1）（2+1）（1+1）=24（个）；

又如：10500=22×3×53×7，

其约数的个数为（2+1）（1+1）（3+1）（1+1）=48（个）；

再比如：81=34，则其约数的个数是4+1=5（个），即1，3，9，27，81。

问题：100以内的自然数中，有10个约数的自然数有哪些？

答案只有两个：48=24×3，80=24×5。

由标准分解式，我们还可以得到一个正整数N的所有正约数的和：

当σ1（N）=2N时，N就叫做完全数。如6，28，496，8128等都是完全数。

是否存在奇完全数，是一个至今未解决之猜想。

我们再来看两个概念：

（4）公约数：如果一个整数c既是数a的约数，又是数b的约数，那么c叫做a与b的公约数。如1，2，3，4，6，12就是36和48的公约数。

（5）最大公约数：两个数的公约数中最大的一个，叫做这两个数的最大公约数。如12就是36和48的最大公约数。

一般地，若c是a，b的最大公约数，则记做c=（a，b）

（6）如何求两个数的最大公约数？

方法一：枚举法。将两个数的因数分别一一列出，从中找出其公因数，再从公因数中找出最大的一个，即为这两个数的最大公因数。

例：求30与24的最大公因数。

30的正因数有：1，2，3，5，6，10，15，30。

24的正因数有：1，2，3，4，6，8，12，24。

其中公因数有1，2，3，6，易得其公因数中最大的一个是6，所以30和24的最大公因数是6，即（30，24）=6。

方法二：短除法。短除法就是先写出要求最大公因数的两个数A、B，再画一个短除号，接着在原本写除数的位置写两个数公有的质因数Z（通常从最小的质数开始），然后在短除号的下方写出这两个数被Z整除的商a、b，对a、b重复以上步骤，以此类推，直到最后的商互质为止，再把所有的除数相乘，其积即为A、B的最大公因数。

例如：求72和420的最大公约数。

列出短除法如下：

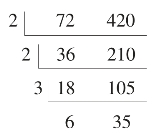
故所求的最大公约数为：2×2×3=12。

而其最小公倍数为：2×2×3×6×35=2520。

方法三：分解质因数法。将需要求最大公因数的两个数A，B分别分解质因数，再从中找出A、B公有的质因数，把这些公有的质因数相乘，即得A、B的最大公约数。

例：求48和36的最大公因数。

把48和36分别分解质因数：

48=2×2×2×2×3=24×3

36=2×2×3×3=22×32

其中48和36公有的质因数有2、2、3，所以48和36的最大公因数是

2×2×3=22×3=12

对于数字较大时，上面的算法也不是很简便，如求（17640，54054）等，有没有较简便的方法呢？答案是肯定的，下面的方法就是一个好方法。

方法四：辗转相除法（欧几里得算法）。

定理：两个整数的最大公约数等于其中较小的那个数和两数相除所得余数的最大公约数。

证明：给定两个整数a，b（a＞b）。若把a表示成a=kb+r（a，b，k，r皆为正整数，且r＜b），这种表示法是唯一的，其中k就是a除以b的商，r就是余数。

假设d是a，b的一个公约数，记作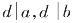，即a和b都可以被d整除。

而r=a-kb，因此d│r，因此d也是b，r的公约数，因此（a，b）和（b，r）的公约数是一样的，其最大公约数也必然相等。

其具体操作方法如下（辗转相除法或欧几里得算法）：

设两整数为a、b，用（a，b）表示a，b的最大公约数。对要求最大公因数的两个数a、b，设b＜a，先用b除a，得a=bq+r1（q是整数，0≤r1＜b）。若r1=0，则最大公因数为（a，b）=b；若r1≠0，则再用r1除b，得b=r1q1+r2（0≤r2＜r1），若r2=0，则（a，b）=r1，若r2≠0，则继续用r2除r1，……，如此循环，直到能整除为止。其最后一个非零余数即为最大公约数（a，b）。

例：求8251和6105的最大公约数。

考虑用较大数除以较小数，求得商和余数：

8251=6105×1+2146

6105=2146×2+1813

2146=1813×1+333

1813=333×5+148

333=148×2+37

148=37×4

最后除数37是148和37的最大公约数，也就是8251与6105的最大公约数。

此计算过程也可以简化为：

（8251，6150）=（6150，2146）=（2146，1813）=（1813，333）

=（333，148）=（148，37）=（37，0）=37

由此也可以算出（17640，54054）=126

中国古代也有类似的计算方法。

方法五：更相减损术。更相减损术出自中国古典名著《九章算术》的一种求最大公约数的算法，它原本是为约分而设计的，但它适用于任何需要求最大公约数的场合。其原文为：“可半者半之，不可半者，副置分母、子之数，以少减多，更相减损，求其等也，以等数约之。”翻译成现代语言就是：

第一步：任意给定两个正整数a、b；判断它们是否都是偶数。若是，则用2约简；若不是则执行第二步。

第二步：以较大的数减较小的数，接着把所得的差与较小的数比较，并以大数减小数。继续这个操作，直到所得的减数和差相等为止。这个数就是a、b的最大公约数。

例：求336与147的最大公约数。

分析：由于147不是偶数，把336和147以大数减小数，并辗转相减：

336-147=189，189-147=42，147-42=105，105-42=63，63-42=21，42-21=21

所以，336和147的最大公约数为21。

“更相减损术”是我国古代重要的数学方法之一，在现代仍有理论意义和使用价值，它奠定了我国渐近分数、不定方程、同余式理论和大衍求一术的理论基础，也是现代“算法”的基础。我国著名数学家吴文俊先生说“这个寓理于算且不证自明的方法，是完全构造性与机械化的，尽可以据此编成程序上机实施”。

以上各方法同样适用于求多个自然数的最大公约数。

例：求120，144，336的最大公约数。

因为（120，144）=24，（144，336）=48，又（24，48）=24，所以，120，144，336的最大公约数是24。

利用算术基本定理，我们可以比较方便地求两个整数的最大公约数和最小公倍数。

例：求2205，18900的最大公约数和最小公倍数。

解：因为2205=32×5×72

18900=22×33×52×7

所以，最大公约数（2205，18900）=32×5×7=315

最小公倍数[2205，18900]=22×33×52×72=132300

由此还可得到下面的重要关系式：

给定任意两个正整数a，b，设最大公约数是（a，b），最小公倍数是[a，b]，

则：a·b=（a，b）×[a，b]

对于二元一次不定方程，最大公约数也有它的应用。

如求不定方程18x+84y=652的整数解，由于（18，84）=6，而6不能整除652，所以此方程无整数解；

如果把方程改写成18x+84y=642，由于6能整除642，所以此方程有解，方程可化简为：3x+14y=107，其通解为。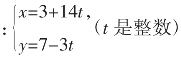

下面我们来举两个例子。

例1：一块钢板，长13.5米，宽10.5米，现把它截成同样大小的正方形，要求正方形最大，并且不需剩下钢板，求正方形的边长。

解：先把每个数扩大十倍，变成135和105，问题就是要求长和宽的最大公约数，用更相减损术得

（135，105）=（105，30）=（30，75）=（30，45）=（30，15）=（15，15）=15

所以，所求正方形的边长是1.5米。

例2：一座大礼堂，内装有100盏电灯，每盏电灯装有一个开关，假设开关的编号为1，2，3，4，…，99，100。现有100位同学依次进入大礼堂，刚开始大礼堂内的所有灯都是灭的。第一个同学进入后把所有的开关全部打开，则灯全部处于亮的状态；第二位同学进入以后，再把编号是2的倍数的开关关闭，此时只有奇数编号的灯是亮着的；第三个同学进入后，再把编号是3的倍数的所有开关均操作一遍，此时亮着的灯又有了变化；第四个同学进入后，再把编号是4的倍数的所有开关再操作一遍。以此类推，当第一百位同学进入后，再把编号是100的开关再操作一下。

问：此时哪些编号的灯是亮着的？

分析：每盏电灯刚开始是灭的，操作1次是亮的，操作2次是灭的，操作3次又是亮的，由此可知，所有最后亮着的灯均是操作了奇数次的灯。也就是说，亮着的灯，其编号的约数的个数必须是奇数个。经观察推理，只有完全平方数的约数的个数才是奇数个。如81=34，所以81的约数有4+1=5个，即1，3，9，27，81。

若要使N是完全平方数，则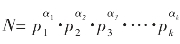中的指数：

α1，α2，α3，…，αk必须全是偶数才行，

因此，N的约数的个数（α1+1）（α2+1）（α3+1）…（αk+1）必是奇数。

因此，最后只有编号是完全平方数的那些灯都是亮的，也就是编号为1，4，9，16，25，36，49，64，81，100的灯均是亮的。

与约数有关的问题还有很多，如前面提到的“完全数”“亲和数”等。
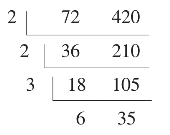
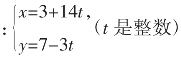