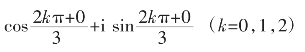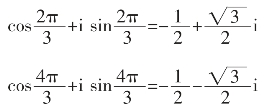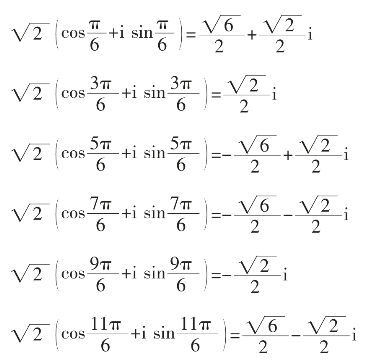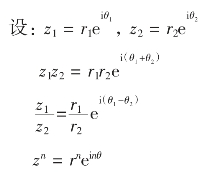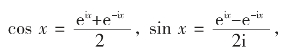虚数的意义与神奇的欧拉公式
数,是数学中最基本的概念,也是人类文明的重要组成部分。一个时代的人们对于数的认识与应用,以及数系理论的完善程度,反映了当时数学发展的水平。数的概念的每一次扩充都标志着数学的一次巨大飞跃。今天,我们所应用的数系,已经构造的如此完备和缜密,以至于在科学技术和社会生活的一切领域中,它都成为基本的语言和不可或缺的工具。在我们得心应手地享用这份人类文明的共同财富时,是否想到在数系形成和发展的历史过程中,人类的智慧所经历的曲折和艰辛呢?
如虚数的出现就是数学史中最奇特的一章,那就是数系的发展历史完全没有按照教科书所描述的逻辑连续性进行,人们也没有等待实数的逻辑基础完全建立之后,才去尝试新的征程。在数系扩张的历史过程中,往往许多中间地带尚未得到完全认识,而天才的直觉随着勇敢者的步伐已经到达了遥远的前哨阵地。正如单位正方形的对角线如何度量,使人们发现了 ,从而把数集由有理数逐步扩展到了无理数,进而使数集由有理数集扩充到了实数集。但同时,实数的运算也还是有一定的局限性,例如-4的平方根在实数范围内就不存在,方程x2+1=0在实数范围内就没有解等。
,从而把数集由有理数逐步扩展到了无理数,进而使数集由有理数集扩充到了实数集。但同时,实数的运算也还是有一定的局限性,例如-4的平方根在实数范围内就不存在,方程x2+1=0在实数范围内就没有解等。
为了解决这一类问题和更多的类似问题,实数集显然是不够的。数学家们经过不断地努力探索,又发现了一种新的数——虚数。数学家们把i定义为虚数单位,并规定i2=-1(或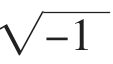 =i),从此一种新的数集诞生了——虚数集合,虚数集合的加入,数集也就从实数集扩充到了复数集,数的概念又得到了进一步的扩充。
=i),从此一种新的数集诞生了——虚数集合,虚数集合的加入,数集也就从实数集扩充到了复数集,数的概念又得到了进一步的扩充。
实数扩充到复数以后,不但解决了负数开偶次方的问题,也使得实系数一元二次方程总可以有解的问题得到解决,而且还使数学发生了质的变化。数字也从一维空间(数轴)扩展到了二维空间(复平面),很多数学问题,尤其是物理中的矢量问题等都得到了有效的解决。
同时,复数在众多数学家和科学家的不断探索和不断完善中,体系更加科学,范围更加广阔,结构更加严谨,并且通过直角坐标平面,把复数与数学中的代数、几何、向量、三角、指数等有机的联系起来,使得复数的表示更加多元,运算更加简便,意义更加多维,解决问题的范围和空间也更加广大。
虚数的出现有其悠久的历史。最早有关虚数方根的文献出于公元1世纪希腊数学家海伦,他考虑的是平顶金字塔不可能问题。而虚数是由意大利米兰学者卡尔达诺在十六世纪首次引入,后经过达朗贝尔、棣莫弗、欧拉、高斯等数学家的工作,此概念逐渐为数学界所接受。
16世纪意大利米兰学者卡尔达诺(Jerome Cardan,1501—1576)在1545年发表的《重要的艺术》一书中,公布了一元三次方程的一般解法,被后人称之为“卡当公式”。他是第一个把负数的平方根写到公式中的数学家,并且在讨论是否可能把10分成两部分,使它们的乘积等于40时,他把答案写成:

尽管他认为这个表达式是没有意义的、想象的、虚无缥缈的,但他还是把10分成了两部分,并使它们的乘积等于40。
给出“虚数”这一名称的是法国数学家笛卡尔(1596—1650),他在《几何学》(1637年发表)中使“虚的数”与“实的数”相对应,从此,虚数才流传开来。
虚数的出现,和无理数的出现一样,又引起了数学界的一片困惑,当时很多大数学家都不承认虚数。德国数学家莱布尼茨(1646—1716)在1702年说:“虚数是神灵遁迹的精微而奇异的隐蔽所,它大概是存在和虚妄两界中的两栖物”。然而,真理性的东西一定可以经得住时间和空间的考验,最终占有自己的一席之地。
法国数学家达朗贝尔(1717—1783)在1747年指出,如果按照多项式的四则运算规则对虚数进行运算,那么它的结果总是a+bi的形式(a、b都是实数)。
法国数学家棣莫弗(1667—1754)在1722年发现了著名的棣莫佛定理。
欧拉在1748年发现了有名的关系式:eπi+1=0,被称为欧拉公式,并且是他在《微分公式》一文中第一次用i来表示-1的平方根,首创了用符号i作为虚数的单位。
“虚数”实际上不是想象出来的,而它是确实存在的。十八世纪末,虚数渐渐被大多数人接受,当时卡斯帕尔·韦塞尔提出复数(实数与虚数)可看作平面上的一点,使得复数与直角坐标平面上的点建立了对应关系,虚数有了对应的位置表示,虚数不再虚无缥缈。卡斯帕尔·韦塞尔的文章发表在1799年的《哥本哈根学社》上,以当今标准来看,该理论也是相当的清楚和完备。他又考虑球体,得出四元数并以此提出完备的球面三角学理论。数年后,高斯再提出此观点并大力推广,进而奠定了复数在数学中的地位,复数的研究开始高速发展。
经过许多数学家长期不懈的努力和深刻探讨,逐步完善并发展了复数理论,才使得在数学领域游荡了200年的幽灵——虚数,揭去了神秘的面纱,显现出它的本来面目,原来虚数并不“虚”。虚数最终成为了数系大家庭中的一员,从而实数集才扩充到了复数集。
下面我们来看看复数都有哪些表示方法,各有哪些运算特点,能解决哪些基本问题。
1.复数的代数形式
我们把形如a+bi(a,b均为实数)的数称为复数,其中a称为实部,b称为虚部,i称为虚数单位,且i2=-1。
当虚部等于零时,即b=0,这个复数就是实数a;
当虚部不等于零时,即b≠0,这个复数a+bi称为虚数;
当a=0且b≠0时,复数bi就称为纯虚数。
全体复数构成一个集合,用C表示,称为复数集。实数的集合用R表示,显然,实数集就是复数集的一个子集合,即R是C的真子集。
复数集是无序集,不能建立大小顺序。
复数的四则运算规定为:
加法法则:(a+bi)+(c+di)=(a+c)+(b+d)i
减法法则:(a+bi)-(c+di)=(a-c)+(b-d)i
乘法法则:(a+bi)·(c+di)=(ac-bd)+(bc+ad)i
除法法则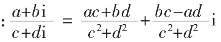 (运算时,分子分母同乘以c-di)
(运算时,分子分母同乘以c-di)
复数代数形式的四则运算,完全可以按照多项式的四则运算来进行,只是遇到i2就用-1来代换,最终的运算结果均可以表示为m+ni(m、n是实数)的形式,仍然是一个复数。
关于虚数单位i的运算规律,我们可以总结如下:
i1=i,i2=-1,i3=-i,i4=1,i5=i,i6=-1,…
则:i4n=1,i4n+1=i,i4n+2=-1,i4n+3=-i(n是自然数)。
由此可知,i的n次幂具有周期性,且周期是4。
而且,i4n+i4n+1+i4n+2+i4n+3=0
例如:计算i+i2+i3+i4+i5+…+i2007+i2018=i+i2=-1+i
例1:已知x2+x+1=0,求x14+x-14的值。
分析:对于方程x2+x+1=0,由于Δ=12-4×1×1=-3<0,故原方程无实数根。
另一方面,(x2+x+1)(x-1)=x3-1=0,所以x3=1(x≠1)
故,x14+x-14=(x3)4x2+(x3)-5x1=x2+x=-1
实际上,x2+x+1=0,x是1的两个虚立方根,即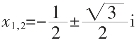 。
。
关于1的两个虚立方根,它们还有一些特殊的性质:
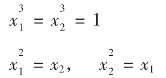
x1x2=1,x1+x2+1=0
上面例子的解法中,隐含了一元二次方程的虚根。
过去我们知道,实系数一元二次方程ax2+bx+c=0(a≠0),当b2-4ac<0时,方程没有实数根,但在复数范围内,这个方程就会有解。
我们来看实系数一元二次方程:
ax2+bx+c=0(a≠0),当b2-4ac<0时,
方程就有两个虚根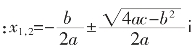 。
。
如方程x2+2x+2=0的两个虚根就是:x=-1±i;
同样,方程x2+1=0的两个虚根就是:x=±i;
结论:实系数一元二次方程如果有两个虚根,那么它们一定是成对出现的,即两个虚根的形式一定是:m±ni(m、n是实数),称为一对共轭复数。
所谓的共轭复数,就是两个复数的实部相等,虚部互为相反数。
共轭复数还有如下的一些性质:
设:z=a+bi,共轭复数设为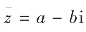
则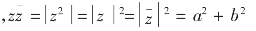
同样,如果实系数一元二次方程ax2+bx+c=0(a≠0)有两个虚根,则仍然满足根与系数的关系定理,即韦达定理:
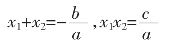
例2:如果3+2i是实系数一元二次方程x2+3bx+c=0的一个根,求方程的另一个根和实数b、c的值。
解:由于实系数一元二次方程的虚根成对出现,可知方程的另一个根是3-2i,
再由韦达定理可知,(3+2i)+(3-2i)=-3b,所以b=-2
(3+2i)·(3-2i)=c,所以c=13
2.复数的几何形式
德国数学家阿甘得(1777—1855)在1806年公布了复数的图象表示法,即所有的实数能用一条数轴表示,同样,复数也能用一个平面上的点来表示。在直角坐标系中,横轴上取对应实数a的点,纵轴上取对应实数b的点,并过这两点引平行于坐标轴的直线,它们的交点Z就表示复数a+bi。像这样,由各点都对应复数的平面叫做“复平面”,后来又称“阿甘得平面”。
复平面实际上就是直角坐标平面,只是原点不是横轴与纵轴的公共点,而只是横轴上的点。如图:
x轴称为实轴,x轴上所有的点与全体实数是一一对应关系。
y轴称为虚轴(除去原点O),y轴上所有的点与纯虚数是一一对应关系。
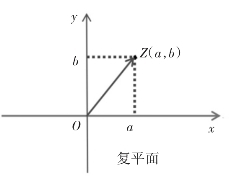
设Z是复平面上任意一点,其横坐标是a,纵坐标是b,链接OZ,则复数可用向量表示为:
也可用点Z(a,b)表示复数:a+bi=(a,b)。
由此可知,全体复数与复平面上以原点为起点的向量是一一对应关系;
同样全体复数与复平面上的点也是一一对应关系。
这就是复数的几何表示。其运算关系为:
设:z1=(a,b),z2=(c,d)
则,z1+z2=(a+c,b+d)
z1-z2=(a-c,b-d)
z1·z2=(ac-bd,bc+ad)
如果复数用向量表示,其加、减运算关系可以用向量的“平行四边形法则”或“三角形法则”来进行。如图:
设 分别与复数a+bi,c+di对应,即
分别与复数a+bi,c+di对应,即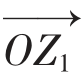 =(a,b)
=(a,b)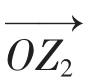 =(c,d),则有:
=(c,d),则有:

 +
+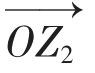 =(a+b,c+d)
=(a+b,c+d)
以OZ1,OZ2为邻边,作平行四边形OZ1ZZ2,则对角线OZ所表示的向量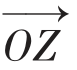 即为复数a+bi与c+di的和。
即为复数a+bi与c+di的和。
即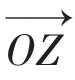 =
=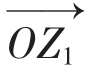 +
+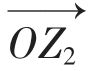 =(a+b,c+d)
=(a+b,c+d)
所以复数的加法可以按照向量的加法来进行(即平行四边形法则)。
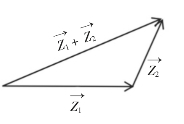
当然,复数的加法也可按照向量的三角形法则进行。如图所示:
两个复数相加,其对应的向量通过平移让它们首尾相接,即第二个向量的起点通过平移与第一个向量的终点重合,然后连接第一个向量的起点与第二个向量的终点,方向指向第二个向量的终点,此向量即为所求的和向量。
3.复数的三角形式
高斯作为伟大的数学家,他对数学的贡献是多方面的。“复数”这个名词就是高斯在1832年第一次提出的。他还把数轴上的点与实数的一一对应关系,扩展为平面上的点与复数一一对应。高斯不仅把复数看作平面上的点,而且还看作是一种向量,并利用复数与向量之间一一对应的关系,阐述了复数的几何加法与乘法。他还将表示平面上同一点的两种不同方法——直角坐标法和极坐标法加以综合,统一用于表示同一复数的几何式和三角式两种形式中,至此,复数理论才比较完整和系统地建立起来了。所以复平面也叫高斯平面。
下面我们来看复平面与复数三角形式的建立。
设复数z=a+bi对应向量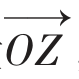 ,向量
,向量 与x轴正半轴所成的角设为θ,向量
与x轴正半轴所成的角设为θ,向量 的长度叫做向量的模,设为r,记做
的长度叫做向量的模,设为r,记做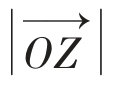 =r,
=r,
则z=a+bi=r cosθ+ir sinθ
即z=r(cosθ+i sinθ)
这就是复数的三角形式。其中θ叫做复数的幅角,r叫做复数的模或绝对值。
任意一个不为零的复数的辐角有无限多个值,且这些值相差2π的整数倍。把适合于-π≤θ<π的辐角θ的值,叫做辐角的主值,记作arg z。辐角的主值是唯一的。
从复数的代数形式和三角形式中,我们可以得到:


tanθ=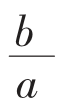 (a≠0,θ的确定看点Z所在的象限。)
(a≠0,θ的确定看点Z所在的象限。)
如:1-i=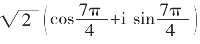 (复数所对应的点在第四象限。)
(复数所对应的点在第四象限。)
或:1-i=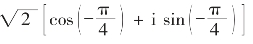
下面我们来看复数的三角形式的乘法、除法、乘方和开方运算。
设z1=r1(cosθ1+i sinθ1),z2=r2(cosθ2+i sinθ2)
则z1z2=r1(cosθ1+i sinθ1)r2(cosθ2+i sinθ2)
=r1r2[(cosθ1cosθ2-sinθ1sinθ2)+i(sinθ1cosθ2+sinθ2cosθ1)]
=r1r2[cos(θ1+θ2)+i sin(θ1+θ2)]
由此可知,两个复数相乘,积的模是两个复数的模的积,积的幅角是两个复数的幅角的和。
同样,两个复数相除,其结果如下:
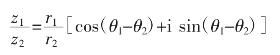
也就是说,两个复数相除,商的模是两个复数模的商,商的幅角是两个复数的幅角的差。
关于乘法运算我们还可以推广到n个复数相乘,其结果是,模是n个复数的模相乘,幅角是n个复数的幅角的和。
进而得到著名的棣莫弗定理:
若z=r(cosθ+i sinθ)
则zn=rn(cos nθ+i sin nθ)(其中n是正整数)
也就是说,一个复数的n次方等于其模的n次方,幅角的n倍。
由此我们看到,复数的三角形式使复数的乘、除法运算和乘方运算变得简便,而且还能使运算降级,乘积是幅角相加,相除是幅角相减,乘方是原幅角的n倍。
例如:
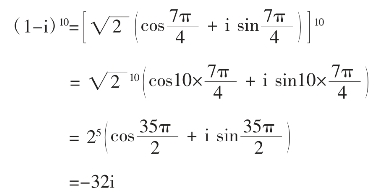

棣莫弗
棣莫弗(De Moivre,Abraham),1667年5月26日生于法国维特里的弗朗索瓦,1754年11月27日卒于英国伦敦,著名数学家。棣莫弗出生于法国的一个乡村医生之家,其父一生勤俭,以行医所得勉强维持家人温饱。棣莫弗自幼接受父亲的教育,稍大后进入当地一所天主教学校念书,这所学校宗教气氛不浓,学生们得以在一种轻松、自由的环境中学习,这对他的性格产生了重大影响。随后,他离开农村,进入色拉的一所清教徒学院继续求学,学校清规戒律较严,也不重视数学教育,但棣莫弗常常偷偷地学习数学。在早期所学的数学著作中,他最感兴趣的是C-惠更斯(Huygens)关于赌博的著作,特别是惠更斯于1657年出版的《论赌博中的机会》(Deratiociniis in ludo aleae)一书,启发了他的灵感。1684年,棣莫弗来到巴黎,幸运地遇见了法国杰出的数学教育家、热心传播数学知识的J.奥扎拉姆(Ozanam)。在奥扎拉姆的鼓励下,棣莫弗学习了欧几里得(Euclid)的《几何原本》(Ele-ments)及其他数学家的一些重要数学著作。1686年棣莫弗到了英国,而后棣莫弗一直生活在英国,他对数学的所有贡献全是在英国做出的。抵达伦敦后,棣莫弗立刻发现了许多优秀的科学著作,于是如饥似渴地学习。一个偶然的机会,他读到了牛顿刚刚出版的《自然哲学的数学原理》(Mathematical principles of natural philosophy),深深地被这部著作吸引了。1692年,棣莫弗拜会了英国皇家学会秘书E.哈雷(Halley),哈雷将棣莫弗的第一篇数学论文“论牛顿的流数原理”(On Newton’s doctrine of fluxions)在英国皇家学会上宣读,引起了学术界的注意。1697年,棣莫弗当选为英国皇家学会会员。棣莫弗的天才及成就逐渐受到了人们广泛的关注和尊重。牛顿对棣莫弗也十分欣赏,据说,后来遇到学生向牛顿请教概率方面的问题时,他就说,这样的问题应该去找棣莫弗,他对这些问题的研究比我深入得多。1735年,棣莫弗被选为柏林科学院院士。1754年,又被法国的巴黎科学院接纳为会员。
我们再来看复数的开方法则:
设zn=r(cosθ+i sinθ),则
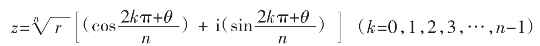
则z叫做复数r(cosθ+i sinθ)的n次方根。显然,一个复数的n次方根有n个,它们的模都相等,幅角相差2π/n的整数倍。
它们所对应的点在以原点为圆心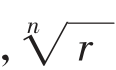 为半径的圆周上,并且把圆周分成n等份。
为半径的圆周上,并且把圆周分成n等份。
我们来看几个例子。
例1:求1的立方根。
设:1=cos 0+i sin 0,则1的立方根是:
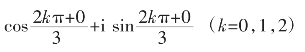
即得1的3个立方根是:cos 0+i sin 0=1
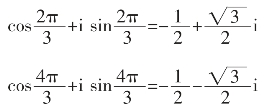
例3:求-8的6次方根。
设:-8=8(cosπ+i sinπ),则-8的6次方根是:

即得-8的6个6次方根是:
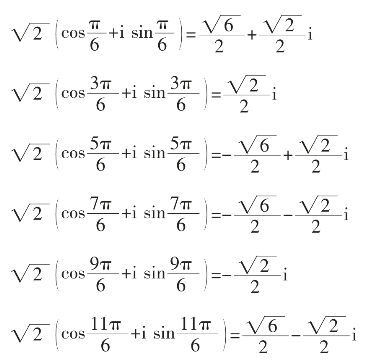
由此可以看出,复数的三角形式便于做复数的乘、除、乘方、开方运算。
复数集不同于实数集的最大特点是,开方运算永远可行,而且一个复数的n次方根一定有n个不同的方根。
由此进一步得到,如下的一元n次复系数方程总有n个根(重根按重数计)。
anxn+an-1xn-1+an-2xn-2+…+a1x+a0=0(an≠0)
4.复数的指数形式
将复数的三角形式z=r(cosθ+isinθ)中的cosθ+isinθ换为eiθ,复数就表为指数形式。即
z=r(cosθ+isinθ)=reiθ
如,eix=cos x+i sin x,e是自然对数的底,i是虚数单位。它将三角函数的定义域扩大到复数,建立了三角函数和指数函数的关系,它在复变函数论里占有非常重要的地位。
用指数形式表示复数,使复数的乘、除、乘方、开方等运算和书写都极其简便。
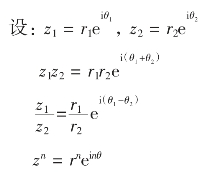
将eix=cos x+i sin x中的x取作π或2π,就得到:
eπi+1=0或e2πi=1
这个恒等式叫做欧拉公式,它是数学里最令人着迷的一个公式,它将数学里最重要的几个数字联系到了一起:两个超越数,一个是自然对数的底e,一个是圆周率π;两个单位:虚数单位i和自然数的单位1,以及被称为人类伟大发现之一的0。数学家们评价它是“上帝创造的公式”
如果将eix=cos x+i sin x里的x换成-x,就可得到e-ix=cos x-isin x,然后采用两式相加减的方法也可进一步推出:
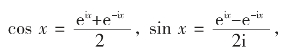
这两个公式也叫做欧拉公式。

莱昂哈德·欧拉
莱昂哈德·欧拉(Leonhard Euler),瑞士大数学家、自然科学家。1707年4月15日出生于瑞士的巴塞尔,1783年9月18日于俄国圣彼得堡去世。欧拉出生于牧师家庭,自幼受父亲的影响。13岁时入读巴塞尔大学,15岁大学毕业,16岁获得硕士学位。欧拉是18世纪数学界最最杰出的人物之一。他不但为数学界作出贡献,更把整个数学推至物理的领域。他还是数学史上最多产的数学家,平均每年写出八百多页的论文,还写了大量的力学、分析学、几何学、变分法等课本,如《无穷小分析引论》《微分学原理》《积分学原理》等都成为数学界中的经典著作。此外欧拉还涉及建筑学、弹道学、航海学等领域。瑞士教育与研究国务秘书Charles Kleiber曾表示:“没有欧拉的众多科学发现,今天的我们将过着完全不一样的生活。”法国数学家拉普拉斯则认为:读读欧拉,他是所有人的老师。欧拉渊博的知识,无穷无尽的创作精力和空前丰富的著作,都是令人惊叹不已的!他从19岁开始发表论文,直到76岁,半个多世纪写下了浩如烟海的书籍和论文。如今几乎每一个数学领域都可以看到欧拉的名字,从初等几何的欧拉线,多面体的欧拉定理,立体解析几何的欧拉变换公式,四次方程的欧拉解法到数论中的欧拉函数,微分方程中的欧拉方程,级数论的欧拉常数,变分学的欧拉方程,复变函数的欧拉公式等,数也数不清。欧拉也是科学史上最多产的一位杰出的数学家,据统计他那不倦的一生,共写下了886本书籍和论文,彼得堡科学院为了整理他的著作,足足忙碌了四十七年。
数系理论的历史发展表明,数的概念的每一次扩张都标志着数学的进步,但是这种进步并不是按照数学教科书的逻辑步骤展开的。希腊人关于无理数的发现暴露出有理数系的缺陷,而实数系的完备性一直要到19世纪才得以完成。回顾数系的历史发展,当人们澄清了复数的概念后,新的问题是:是否还能在保持复数基本性质的条件下对复数进行新的扩张呢?答案是否定的。当哈米尔顿试图寻找三维空间复数的类似物时,他发现自己被迫要做两个让步:第一,他的新数要包含四个分量;第二,他必须牺牲乘法交换律。这两个特点都是对传统数系的革命。他称这新的数为“四元数”。“四元数”的出现昭示着传统观念下数系扩张的结束。数系的扩张虽然就此终止,但是,通向抽象代数的大门被打开了。
随着科学和技术的进步,复数理论已越来越显出它的重要性,它不但对于数学本身的发展有着极其重要的意义,而且在科技领域应用更为广泛,如为证明机翼上升力的基本定理起到了重要作用,并在解决堤坝渗水的问题中显示了它的威力,也为建立大型水电站提供了重要的理论依据等。
 ,从而把数集由有理数逐步扩展到了无理数,进而使数集由有理数集扩充到了实数集。但同时,实数的运算也还是有一定的局限性,例如-4的平方根在实数范围内就不存在,方程x
,从而把数集由有理数逐步扩展到了无理数,进而使数集由有理数集扩充到了实数集。但同时,实数的运算也还是有一定的局限性,例如-4的平方根在实数范围内就不存在,方程x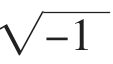 =i),从此一种新的数集诞生了——虚数集合,虚数集合的加入,数集也就从实数集扩充到了复数集,数的概念又得到了进一步的扩充。
=i),从此一种新的数集诞生了——虚数集合,虚数集合的加入,数集也就从实数集扩充到了复数集,数的概念又得到了进一步的扩充。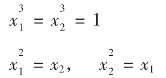
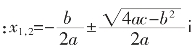 。
。
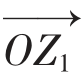 =(a,b)
=(a,b)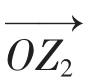 =(c,d),则有:
=(c,d),则有:
 +
+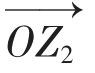 =(a+b,c+d)
=(a+b,c+d)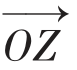 即为复数a+bi与c+di的和。
即为复数a+bi与c+di的和。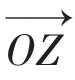 =
=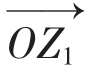 +
+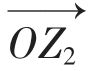 =(a+b,c+d)
=(a+b,c+d)
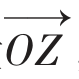 ,向量
,向量 与x轴正半轴所成的角设为θ,向量
与x轴正半轴所成的角设为θ,向量 的长度叫做向量的模,设为r,记做
的长度叫做向量的模,设为r,记做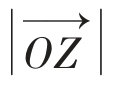 =r,
=r,
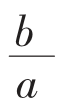 (a≠0,θ的确定看点Z所在的象限。)
(a≠0,θ的确定看点Z所在的象限。)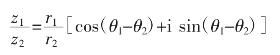
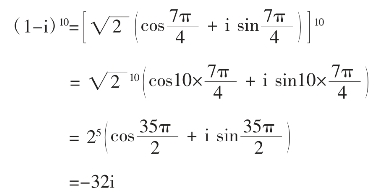

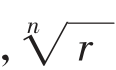 为半径的圆周上,并且把圆周分成n等份。
为半径的圆周上,并且把圆周分成n等份。