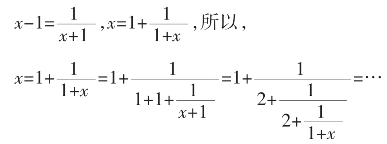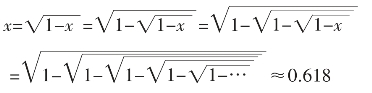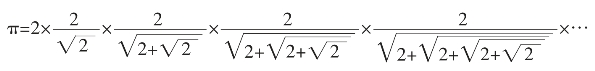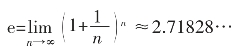-
1.1自序 爱上数学
-
1.2他序 开启数学王国的钥匙
-
1.3目录
-
1.4数的发展与魅力
-
1.4.1数字是个大家庭
-
1.4.2有个性的数字
-
1.4.3素数知多少
-
1.4.4无理数与连分数
-
1.4.5虚数的意义与神奇的欧拉公式
-
1.5古算经典
-
1.5.1算术基本定理与辗转相除法
-
1.5.2韩信将兵与中国剩余定理
-
1.5.3鸡兔同笼与中国古算经
-
1.5.4百钱买百鸡与丢番图方程
-
1.5.5兔子繁殖与斐波那契数列
-
1.6魅力常数
-
1.6.1圆周率与祖氏子孙
-
1.6.2黄金分割与华罗庚优选法
-
1.6.3银行利率与自然常数e
-
1.7神奇妙算
-
1.7.1九九乘法口诀表的魅力
-
1.7.2从印度数学看神奇妙算
-
1.7.3无字的证明
-
1.7.4最大与最小,最远与最近
-
1.7.5刘徽割圆术与极限思想
-
1.8猜想与定理
-
1.8.1哥德巴赫猜想与陈氏定理
-
1.8.2从费马猜想到费马大定理
-
1.8.3多面孔的柯西不等式
-
1.8.4杨辉三角形与二项式定理
-
1.9几何经典问题
-
1.9.1千古第一定理——勾股定理
-
1.9.2三角形到底有多少“心”?
-
1.9.3没有规矩不成方圆
-
1.9.4三角形内角和可以不是180度
-
1.10数学与文化
-
1.10.1数字与文化生活
-
1.10.2河图洛书与幻方
-
1.10.3历法与日历中的数学
-
1.10.4数学与诗词
-
1.10.5数学有大美
-
1.10.6三段论与演绎推理
-
1.10.7数学家就是哲学家
-
1.11后记一 “书香之家”——温馨的荣誉
-
1.12后记二 天道有情
-
1.13后记三 数学是科学之王
-
1.14附:社会评价
-
1.15参考书目
1
爱上数学
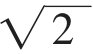 是无理数。
是无理数。 是有理数,必有
是有理数,必有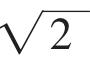 是无理数。
是无理数。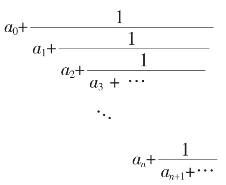
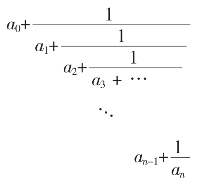
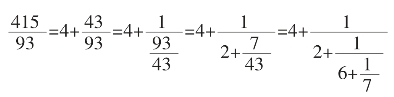
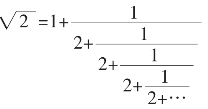
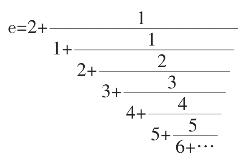
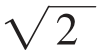 的连分数表示:
的连分数表示: