素数知多少
自然数是人们认识数的开始,也是最基本、最简单的数系。但是自然数中却有着无穷的魅力,研究自然数的专门学科被称为数论,也被称为数学中的皇冠。自然数中的很多“猜想”,吸引了无数数学家为之奋斗,有些猜想已经被证明,如费马猜想,有些猜想至今还没有得到完全证明,如哥德巴赫猜想。但是,通过猜想的证明与探索,产生的很多新的数学理论、数学方法,却是猜想者没有料到的,这些才是对数学的最大贡献。
自然数中对素数的研究,应该是自然数中最有魅力的课题之一,看似简单的素数,却牵动着无数数学家及爱好者为之探索,很多问题至今还没有答案。下面介绍几个与素数相关的问题与读者分享。
1.认识素数
自然数的分类有很多种方法,比如可以分为奇数与偶数两类,也可以分为完全平方数和非完全平方数等。而其中还有一种分法就是按自然数因数的个数来分,可分为素数(质数)、合数和单位数1。
素数:除了1和它本身这两个因数外,再没有其他因数的自然数叫做素数。
如,2,3,5,7,11,13,17,19,23,等等。素数中只有一个是偶数,就是2,其余的素数都是奇数。
合数:除了1和它本身外还有其他的因数的自然数叫做合数。
如,4,6,8,9,10,12,14,15,等等,除2以外,偶数一定是合数。
而每一个合数又都可以分解成若干个素数相乘的形式。这就是著名的“整数唯一分解定理”。这个定理说,所有大于1的整数都只能被唯一地分解成质数的乘积。如:
12=22×3
1800=23×32×52
1651104=25×34×72×13
单位数,只有1个因数,就是1,它既不是素数也不是合数。
素数是人们研究的热点之一,下面给出1000以内的所有素数。
2 3 5 7 11 13 17 19
23 29 31 37 41 43 47 53
59 61 67 71 73 79 83 89
97 101 103 107 109 113 127 131
137 139 149 151 157 163 167 173
179 181 191 193 197 199 211 223
227 229 233 239 241 251 257 263
269 271 277 281 283 293 307 311
313 317 331 337 347 349 353 359
367 373 379 383 389 397 401 409
419 421 431 433 439 443 449 457
461 463 467 479 487 491 499 503
509 521 523 541 547 557 563 569
571 577 587 593 599 601 607 623
617 619 631 641 643 647 653 659
661 673 677 683 691 701 709 719
727 733 739 743 751 757 761 769
773 787 797 809 811 821 823 827
829 839 853 857 859 863 877 881
883 887 907 911 919 929 937 941
947 953 967 971 977 983 991 997
2.寻找素数
寻找素数没有什么特别的规律可循,也没有一个公式能表示所有的素数。一种寻找素数的基本方法就是古希腊所谓的“埃拉托斯特尼筛法”。
其具体做法是:给出要筛数值的范围n,找出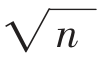 以内的所有素数2,3,p3,p4,…,pk。先用2去筛,即把2留下,把2的倍数剔除掉;再用下一个素数,也就是3去筛,把3留下,把3的倍数剔除掉;接下去用下一个素数5筛,把5留下,把5的倍数剔除掉;依次重复下去,最后用pk筛,把pk留下,把pk的倍数剔除掉,剩下的数就是所要找的小于或等于n的所有素数。
以内的所有素数2,3,p3,p4,…,pk。先用2去筛,即把2留下,把2的倍数剔除掉;再用下一个素数,也就是3去筛,把3留下,把3的倍数剔除掉;接下去用下一个素数5筛,把5留下,把5的倍数剔除掉;依次重复下去,最后用pk筛,把pk留下,把pk的倍数剔除掉,剩下的数就是所要找的小于或等于n的所有素数。
根据数学家证明,素数的个数是无穷的。
欧几里得的《几何原本》中有一个经典的证明,它使用了证明常用的间接方法,即反证法。具体证明如下:
假设素数只有有限的n个,从小到大依次排列为p1,p2,…,pn,
设N=p1×p2×…×pn,那么,pn+1是素数或者不是素数。
如果pn+1为素数,则pn+1要大于p1,p2,…,pn,所以它不在那些假设的素数集合中。
如果pn+1为合数,因为任何一个合数都可以分解为几个素数的积;而N和N+1的最大公约数是1,所以pn+1不可能被p1,p2,…,pn整除,所以该合数分解得到的素因数肯定不在假设的素数集合中。
因此无论该数是素数还是合数,都意味着在假设的有限个素数之外还存在着其他素数。所以原先的假设不成立。也就是说,素数有无穷多个。
关于素数有无穷多个,其他数学家也给出了一些不同的证明,在此不再赘述。
3.素数的独特的性质
(1)素数p的约数只有两个:1和p。
(2)初等数学基本定理:任一大于1的自然数,要么本身是素数,要么可以分解为几个素数之积,且这种分解是唯一的。
(3)素数的个数是无限的。
(4)若n为正整数,在n2到(n+1)2之间至少有一个素数。
如在102和112之间,即在100和121之间就有101、103、107、109、113五个素数。
(5)若n为大于或等于2的正整数,在n到n!之间至少有一个素数。
如6!=6×5×4×3×2×1=720,在6与720之间至少有一个素数,如7,11,13,…,701,709,719等。
(6)所有大于10的素数中,个位数只有1,3,7,9。
(7)形如4k+1的素数可以唯一的表示为两个数的平方和(费马证明);
例如:5=12+22,13=22+32,17=12+42,29=22+52,…
但是形如4k+3的素数就不能表示为两个数的平方和。
4.孪生素数
孪生素数就是指相差2的素数对,例如在1到100之间的孪生素数依次是:3和5,5和7,11和13,17和19,29和31,41和43,59和61,71和73等。
孪生素数猜想,该猜想正式由德国著名数学家希尔伯特在1900年国际数学家大会的报告中提出,猜想可以这样描述:
存在无穷多个素数p,使得p+2是素数。素数对(p,p+2)称为孪生素数。
古希腊数学家欧几里得也曾经提出,存在无穷多对素数,他们只相差2。
随着素数的增大,下一个素数离上一个素数应该越来越远,寻找大的孪生素数也就比较困难。但有时也不一定,例如
2003663613×2195000-1和2003663613×2195000+1就是一对孪生素数。
素数在趋于无穷大时变得越来越少,而孪生素数,与素数一样,也有相同的趋势,并且这种趋势比素数更为明显。由于孪生素数猜想的高知名度以及它与哥德巴赫猜想的联系,因此不断有学术共同体外的数学爱好者试图证明它。有些人声称已经证明了孪生素数猜想。然而,尚未出现能够通过专业数学工作者审视的证明。
目前已知最大的孪生素数共有388342位数,于2016年9月14日发现,它们是:2996863034895×21290000±1。
1849年,法国数学家阿尔方·德·波利尼亚克提出了更一般的猜想:对所有自然数k,存在无穷多个素数对(p,p+2k)。k=1的情况就是孪生素数猜想。因此,波利尼亚克有时也被认为是孪生素数猜想的提出者。
孪生素数猜想就是指“孪生素数有无穷多个”,这个猜想至今仍未被证明。
5.费马素数
对于任意非负整数n,由下式定义的数
Fn=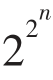 +1
+1
称为费马数(因为费马最早研究了这类数),前五个费马数是:
F0=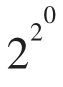 +1=3
+1=3
F1=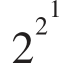 +1=5
+1=5
F2= +1=17
+1=17
F3=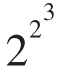 +1=257
+1=257
F4=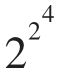 +1=65537
+1=65537
容易验证,它们全都是素数,由此费马猜想,对于所有非负整数n,Fn都是素数。因为在Fn的表达式中,n是指数的指数,Fn随着n极快地增大,当n=5时,它就已经是一个十位数了,在没有计算器和电脑的时代,单靠手算要验证它是不是一个素数是一件十分辛苦的事情,费马于是就轻率地相信了他的直觉,并未加以检验。
可惜这一次费马猜错了(费马的绝大多数猜想后来都被证明是正确的)。
1732年,在费马提出这一猜想的近百年后,瑞士大数学家欧拉证明了F5不是素数,因为,
F5= +1=232+1=4294967297=641×6700417
+1=232+1=4294967297=641×6700417
这就推翻了费马的猜想。只要稍加尝试你就会发现,要用筛法发现4294967297的一个素因子是多么困难。找到素因子641,欧拉自然用了巧思而不是蛮力,实际上,他用的正是费马的另一个猜想——费马小定理。
后来,人们又陆续找到了更多不是素数的费马数。相反,费马素数的数量却仍然只有上面这五个。于是人们又反过来猜测,除了这五个费马数是素数,其余的费马数全都是合数(但至今未能证明这个猜想)。
如,接下来的两个费马数是:
F6= +1=264+1=18446744073709551617=274177×67280421310721
+1=264+1=18446744073709551617=274177×67280421310721
F7=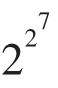 +1=2128+1=340282366920938463463374607431768211457=59649589127497217×5704689200685129054721
+1=2128+1=340282366920938463463374607431768211457=59649589127497217×5704689200685129054721
6.梅森素数
梅森素数是由梅森数而来。
所谓梅森数,是指形如2p-1的一类数,其中指数p是素数,常记为Mp。如:3=22-1,7=23-1,31=25-1,127=27-1,2047=211-1等。如果梅森数是素数,就称为梅森素数。梅森验算出:当p=2,3,5,7,17,19时,所得的代数式的值都是素数。但p=11时,所得2047=23×89却不是素数。

马林·梅森
梅森素数是以17世纪法国著名数学家马林·梅森的名字命名的。由多国科学家组成的评审委员会遴选出了100位在世界科学史上有重要地位的科学家,大名鼎鼎的亚里士多德、阿基米德、哥白尼、伽利略、笛卡尔、牛顿、达尔文、爱因斯坦等入选,马林·梅森也名列其中。由于梅森学识渊博、才华横溢、为人热情以及最早系统而深入地研究2p-1型的数,为了纪念他,数学界就把这种数称为“梅森数”,并以Mp记之(其中M为梅森姓名的首字母),即Mp=2p-1。如果梅森数为素数,则称之为“梅森素数”(即2p-1型素数)。
后来,欧拉证明p=31时,2p-1是素数。梅森去世250年后,美国数学家科尔证明,267-1=193707721×761838257287,是一个合数。
但是,素数排列的杂乱无章,也给人们寻找素数规律造成了困难。
梅森素数是数论研究中的一项重要内容,自古希腊时代起人们就开始了对梅森素数的探索。由于这种素数具有独特的性质(比方说和完全数密切相关)和无穷的魅力,千百年来一直吸引着众多数学家(包括欧几里得、费马、欧拉等)和无数的数学爱好者对它进行探究。
用因式分解法可以证明,若2n-1是素数,则指数n也是素数;反之,当n是素数时,2n-1(即Mp)却未必是素数。前几个较小的梅森数大都是素数,然而梅森数越大,梅森素数也就越难出现。
是否存在无穷多个梅森素数是数论中未解决的著名难题之一。
梅森素数排列极其稀少,截至目前,也仅发现了49个梅森素数,最大的是274207281-1(即2的74207281次方减1),有22338618位数,如果用普通字号将这个巨数连续写下来,其长度可超过50公里!
下面列出前10个梅森素数Mp:
(1)p=2,M2=22-1=3;
(2)p=3,M3=23-1=7;
(3)p=5,M5=25-1=31;
(4)p=7,M7=27-1=127;
(5)p=13,M13=213-1=8191;
(6)p=17,M17=217-1=131071;
(7)p=19,M19=219-1=524287;
(8)p=31,M31=231-1=2147483647;
(9)p=61,M61=261-1=2305843009213693951;
(10)p=89,M89=289-1=618970019642690137449562111(27位数)。
2013年1月,美国中央密苏里大学数学教授柯蒂斯·库珀领导的研究小组发现了第48个梅森素数257885161-1。这一发现被英国《新科学家》周刊评为当年自然科学十大突破之一。
2016年1月7日,库珀又发现第49个梅森素数274207281-1。这个超大素数有22338618位,是目前已知的最大素数。这已是库珀第四次通过GIMPS(因特网梅森素数大搜索)项目发现新的梅森素数。由于这种素数珍奇而迷人,它被人们称为“数学珍宝”。
值得一提的是,中国数学家和语言学家周海中教授根据已知的梅森素数及其排列,巧妙地运用联系观察法和不完全归纳法,于1992年正式提出了梅森素数分布的猜想,这一重要猜想被国际上称为“周氏猜测”。
“周氏猜测”:当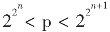 时,Mp有2n+1-1个是素数。其中,n为自然数,p为素数,Mp为梅森素数。
时,Mp有2n+1-1个是素数。其中,n为自然数,p为素数,Mp为梅森素数。
如,n=2时,16<p<256,Mp在这个范围内有7个是素数。
即M17,M19,M31,M61,M89,M107,M127均是梅森素数。
寻找梅森素数在当代已有了十分丰富的意义。寻找梅森素数是发现已知最大素数的最有效途径。自欧拉证明M31为当时最大的素数以来,在发现已知最大素数的世界性竞赛中,梅森素数几乎囊括了全部冠军。由于梅森素数的探究需要多种学科和技术的支持,也由于发现新的“大素数”所引起的国际影响,使得对于梅森素数的研究能力已在某种意义上标志着一个国家的科技水平,而不仅仅是代表数学的研究水平。英国顶尖科学家、牛津大学教授马科斯·索托伊甚至认为它的研究进展不但是人类智力发展在数学上的一种标志,同时也是整个科学发展的里程碑之一。
在现代,梅森素数在计算机科学、密码学等领域都有着重要的应用价值。素数被利用在密码学上,即所谓的公钥,就是将想要传递的信息在编码时加入素数,编码之后传送给收信人,任何人收到此信息后,若没有此收信人所拥有的密钥,则解密的过程中(实为寻找素数的过程),将会因为找素数的过程(分解质因数)过久,即使取得信息也会无意义。
在汽车变速箱齿轮的设计上,相邻的两个大小齿轮齿数最好设计成素数,以增加两齿轮内两个相同的齿相遇啮合次数的最小公倍数,可增强耐用度、减少故障。
在害虫的生物生长周期与杀虫剂使用之间的关系上,杀虫剂的素数次数的使用也得到了证明。实验表明,素数次数地使用杀虫剂是最合理的,都是使用在害虫繁殖的高潮期,而且害虫很难产生抗药性。
以素数形式无规律变化的导弹和鱼雷可以使敌人不易拦截。
多数生物的生命周期也是素数(单位为年),这样可以最大限度地减少碰见天敌的机会。
梅森素数这颗数学海洋中的璀璨明珠正以其独特的魅力,吸引着更多的有志者寻找和研究,它还是人类好奇心、求知欲和荣誉感的最好见证。
7.有关素数的猜想
(1)哥德巴赫猜想:是否每个大于4的偶数都可写成两个素数之和?
(2)孪生素数猜想:孪生素数就是差为2的素数对,例如11和13。是否存在无穷多的孪生素数?
(3)斐波那契数列内是否存在无穷多个素数?
(4)是否有无穷多个的梅森素数?
(5)在n2与(n+1)2之间是否每隔n就有一个素数?
(6)是否存在无穷多个形式如x2+1的素数?
8.黎曼猜想
波恩哈德·黎曼(1826年9月17日—1866年7月20日),德国著名数学家、物理学家,对数学分析和微分几何作出了重要贡献,其中一些为广义相对论的发展铺平了道路。他的名字出现在黎曼ζ函数,黎曼积分,黎曼几何,黎曼引理,黎曼流形,黎曼映照定理,黎曼-希尔伯特问题,黎曼思路回环矩阵和黎曼曲面中。黎曼几何的开创,为爱因斯坦的广义相对论提供了数学基础。

波恩哈德·黎曼
黎曼猜想是关于黎曼函数ζ(s)的零点分布的猜想,由数学家黎曼于1859年在他的著名论文《论不大于一个给定值的素数的个数》中提出。也是德国数学家希尔伯特列出的23个世界级数学问题之一,其中第8个问题中便有黎曼猜想。
素数在自然数中的分布并没有简单的规律,黎曼发现素数出现的频率与黎曼函数(ζ(s)=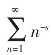 ,其中s=x+yi是复变数)紧密相关。黎曼猜想提出:
,其中s=x+yi是复变数)紧密相关。黎曼猜想提出:
黎曼函数ζ(s)=0的解都应该位于复平面上的直线x=1/2(“临界线”)上。
这个猜想如果能够获得证明,人们就能够精确地找出素数分布的频率及其性状,必将为所有素数研究中待解的问题带来光明。函数论和解析数论中的很多问题都依赖于黎曼猜想,在代数数论中的广义黎曼猜想更是影响深远。若能证明黎曼猜想,则可带动许多问题的解决。可惜至今尚无人给出一个令人信服的关于黎曼猜想的合理证明。
德国著名数学家希尔伯特晚年时曾被人问过一个有趣的问题:“假如您去世后一百年能复活,您首先会做什么呢?”希尔伯特回答“我会先问黎曼猜想是否已经获得解决了?”可见黎曼猜想的魅力。
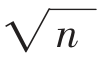 以内的所有素数2,3,p
以内的所有素数2,3,p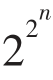 +1
+1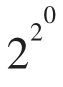 +1=3
+1=3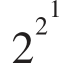 +1=5
+1=5 +1=17
+1=17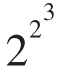 +1=257
+1=257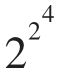 +1=65537
+1=65537 +1=2
+1=2 +1=2
+1=2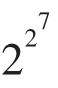 +1=2
+1=2

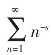 ,其中s=x+yi是复变数)紧密相关。黎曼猜想提出:
,其中s=x+yi是复变数)紧密相关。黎曼猜想提出: