数字是个大家庭
数,是数学中最基本的概念,也是人类文明的重要组成部分。古希腊数学家毕达哥拉斯说:“万物皆数”,认为世界万事万物都离不开数,都可以用数来描述,也都可以用数来刻画。著名科学家爱因斯坦也说:“数字和宇宙同等重要”,认识宇宙离不开数字。我国古代著名哲学家老子也说:“道生一,一生二,二生三,三生万物。”所以,人类的发展离不开数字。
人类是动物进化的产物,最初也完全没有数量的概念。但人类发达的大脑对客观世界的认识已经达到更加理性和抽象的地步。这样,在漫长的生活实践中,由于记事和分配生活用品等方面的需要,就逐渐产生了数的概念。“结绳记事”就是地球上许多古代人类共同做过的事,我国古书《易经》中就有“结绳而治”的记载。传说古代波斯王打仗时也常用绳子打结来计算天数。还有用利器在树皮上或兽皮上刻痕,或用小棍摆在地上计数也都是古人常用的办法,这些办法用得多了,就逐渐形成了数的概念和记数的符号。
数的概念最初不论在哪个地区都是从1,2,3,4,…这样的自然数开始的,但是记数的符号却大不相同。自然数的产生,起源于人类在生产和生活中计数的需要。开始只有很少几个自然数,后来随着生产力的发展和记数方法的改进,逐步认识越来越多的自然数。从某种意义上说,幼儿认识自然数的过程,就是人类祖先认识自然数的过程的再现。
随着生产的发展,生活的需要,在土地使用、天文观测、土木建筑、水利工程等活动中,都需要进行测量。在测量过程中,常常会发生度量不尽的情况,人们发现,仅仅能表示自然数是远远不行的,如果要更精确地度量下去,就必然产生自然数不够用的矛盾。还有如果分配猎获物时,4个人分6件东西,每个人该得多少呢?于是分数就产生了。据数学史书记载,三千多年前埃及纸草书中已经记有关于分数的问题。引进分数,这是数的概念的第一次扩展。
最初人们在记数时,没有“零”的概念。后来,在生产实践中,需要记录和计算的东西越来越多,逐渐产生了位值制记数法。有了这种记数法,零的产生就不可避免了。如我国古代筹算中,利用“空位”表示零。公元6世纪,印度数学家开始用符号“0”表示零。但是,把“0”作为一个数是很迟的事。引进数0,这是数的概念的第二次扩充。
自然数、分数和零,通称为算术数。自然数也称为正整数。
说起“0”的出现,应该指出,我国古代文字中,“零”字出现很早。不过那时它不表示“空无所有”,而只表示“零碎”“不多”的意思。如“零头”“零星”“零丁”等。如“一百零五”的意思是:在一百之外,还有一个零头五。随着阿拉伯数字的引进。“105”恰恰读作“一百零五”,“零”字与“0”恰好对应,“零”也就具有了“0”的含义。
现在,“0”已经成为含义最丰富的数字符号。“0”可以表示没有,也可以表示有。如:气温0℃,并不是说没有气温;“0”是正负数之间唯一的中性数;任何数(0除外)的0次幂等于1,即a0=1(a≠0);0!=1(零的阶乘等于1,定义:n!=n(n-1)(n-2)…3×2×1);等等。
随着社会的发展,人们又发现很多数量具有相反的意义,比如增加和减少,前进和后退,上升和下降,向东和向西。以后,为了表示具有相反意义的量,负数的概念就出现了。我国是认识正、负数最早的国家,在我国汉朝时期的古数学经典《九章算术》中就有了正、负数的记载。在欧洲,直到17世纪才对负数有了一个完整的认识。引进负数,这是数的概念的第三次扩充。
正整数、负整数和零,统称为整数,如果再加上正分数和负分数,就统称为有理数。
有了这些数字,人们计算起来就感到方便多了。
数的概念的又一次扩充渊源于古希腊。但是,在数字的发展过程中,一件不愉快的事发生了。让我们回到2500多年前的古希腊,那里有一个毕达哥拉斯(Pythagqras,约公元前580—前500)学派,是一个研究数学、科学和哲学的团体。他们认为“数”是万物的本源,支配了整个自然界和人类社会。因此世间一切事物都可归结为数或数的比例,这是世界之所以美好和谐的源泉。他们所说的数是指整数和分数,但分数都可以写成两个整数之比,所以他们相信一切数都可以写成两个整数之比。但是学派中有一个叫希帕索斯的学生在研究1与2的比例中项时,发现没有一个能用整数比例写成的数可以表示它。他又画了一个边长为1的正方形,设对角线为x,根据勾股定理(西方称毕达哥拉斯定理)得:x2=12+12=2,由此可知单位正方形的边长与对角线也是不可公度的。可它是多少呢?又该怎样表示这个数呢?可见边长为1的正方形的对角线的长度数肯定是存在的。希帕索斯等人百思不得其解,最后认定这是一个从未见过的新数。
这个新数的出现使毕达哥拉斯学派感到震惊,动摇了他们哲学思想的核心。为了保持支撑世界的数学大厦不坍塌,他们规定对新数的发现要严守秘密。而希帕索斯还是忍不住将这个秘密泄露了出去。据说希帕索斯后来被扔进大海喂了鲨鱼。然而真理是藏不住的,人们后来又发现了很多不能用两整数之比写出来的数,如圆周率就是最重要的一个,人们把它们记成π,称它们为无理数。但当时只是用几何的形象来说明无理数的存在,至于严格的实数理论,直到19世纪70年代才建立起来。
引进无理数,形成实数集,这是数的概念的第四次扩充。
有理数和无理数一起统称为实数。
在实数范围内对各种数的研究使数学理论达到了相当高深和丰富的程度。这时,人类的历史已进入19世纪,许多人认为数学成就已经登峰造极,数字这个大家庭已经圆满收官,数字的形式也不会再有什么新成员的发现了。
然而,人们探索的脚步从来就没有停止过。数的概念的再一次扩充,是为了解决数学自身的矛盾。如在解方程的时候常常需要开平方,如果被开方数是负数,这道题还有解吗?如果没有解,那数学运算就像走在死胡同中那样处处碰壁。16世纪前半叶,意大利数学家塔尔塔利亚发现了三次方程的求根公式,大胆地引用了负数开平方的运算,得到了正确答案。由此,虚数作为一种合乎逻辑的假设得以引进,并在进一步的发展中加以运用,成功地经受了理论和实践的检验,最后于18世纪末至19世纪初确立了“虚数”在数学中的地位。
于是数学家们就规定用符号“i”表示“-1”的平方根,即i2=-1,虚数就这样诞生了,“i”成了虚数的单位。后人将实数和虚数结合起来,写成a+bi的形式(a、b均为实数),这就是复数。而且当b=0时,复数就是实数。
引进虚数,形成复数集,这是数的概念的第五次扩充。
虚数就是虚无缥缈的数吗?在很长一段时间里,人们在实际生活中找不到用虚数和复数表示的量,所以虚数总让人感到虚而不实。随着科学技术的发展,虚数现在在水利学、地图学和航空学上已经有了广泛的应用,在掌握和会使用虚数的科学家眼中,虚数一点也不“虚”了。如复数5i就可以表示为方向正北、长度为5的向量;2-2i就可以表示方向是东南、长度是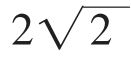 的一个向量了。
的一个向量了。
另一方面,在两千多年的数学发展史中,代数方程的研究也一直是数学家们关注的重点之一,在实际应用和理论研究中,方程的解法和理论也在不断完善。因而从解方程的需要出发,对数系的发展也起着推动作用。如:
(1)解方程3x-5=0,得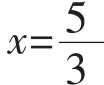 ,这是引进分数的必要;
,这是引进分数的必要;
(2)解方程3x+6=0,得x=-2,这是引进负数的必要;
(3)解方程x2-5=0,得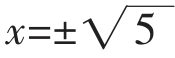 ,这是引进无理数的必要;
,这是引进无理数的必要;
(4)解方程x2+4=0,得x=±2i,这是引进虚数的必要。
引入复数后,任何复系数一元n次多项式方程
anxn+an-1xn-1+an-2xn-2+…+a1x+a0=0(an≠0)
在复数域上至少有一个根,由此推出n次复系数多项式方程在复数域内有且只有n个根(重根按重数计算)。
这就是数学中的“代数学基本定理”。
如方程x3-1=0一定有三个根。它们分别是:
x1=1,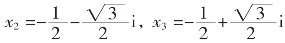
数的概念发展到虚数和复数以后,在很长一段时间内,连某些数学家也认为数的概念已经十分完善了,数学家族的成员已经全部都到齐了。
复数系能否继续扩充?这个问题的答案是有条件的。如果要求完全满足复数系的全部运算性质,那么任何扩充都是难以成功的。如果放弃某些要求,那么进一步的扩充是可能的。
1843年10月16日,英国数学家哈密尔顿又提出了“四元数”的概念。所谓四元数,就是一种形如a+xi+yj+zk的数。它是由一个标量a(实数)和一个向量xi+yj+zk(其中x、y、z为实数)组成的。四元数在数论、群论、量子理论以及相对论等方面有着广泛的应用。
因此,复数系C还可以扩充为四元数系H。
如果再适当改变运算律的要求,四元数系H又可扩充为八元数系Ca等。
当然,在现代数学中,通常总是把“数”理解为复数或实数,只有在个别情况下,经特别指出,才用到四元数,至于八元数的使用就更罕见了。
由于科学技术发展的需要,向量、张量、矩阵、群、环、域等概念不断产生,把数学研究推向新的高峰。人们还开展了对“多元数”理论的研究。多元数已超出了复数的范畴,人们称其为超复数。尽管人们对数的归类法还有某些分歧,但在承认数的概念还会不断发展这一点上意见是一致的。到目前为止,数的家庭已发展得十分庞大。
必须指出,数的概念的产生,实际上是交错进行的。例如,在人们还没有完全认识负数之前,早就知道了无理数的存在。在实数理论还未完全建立之前,已经运用虚数解三次方程了。直到19世纪初,从自然数到复数的理论基础,并未被认真考虑过。后来,由于数学严密性的需要以及公理化倾向的影响,促使人们开始认真研究整个数系的逻辑结构。从19世纪中叶起,经过皮亚诺(G.Peano,1855—1939)、康托尔(G.Cantor,1845—1918)等数学家的努力,才完成了建立整个数系的逻辑工作。
近代数学关于数的理论,是在总结数的历史发展的基础上,用代数结构的观点和比较严格的公理系统加以整理而建立起来的。作为数的理论系统的基础,首先要建立自然数系,然后逐步加以扩展。一般采用的扩展过程是:
N(自然数集)→Z(整数集)→Q(有理数集)→R(实数集)→C(复数集)→H(四元数集)→Ca(多元数集)。
数系的每一次扩充,都解决了一定的矛盾,从而扩大了数的应用范围。
数的运算也非常悠久。我国古代先辈十分重视运算,很早就创造了一种十分重要的计算方法——筹算。筹算用的算筹是竹制的小棍,也有骨制的。按规定的横竖长短顺序摆好,就可用来记数和进行运算。随着筹算的普及,算筹的摆法也就成为记数的符号了。从算筹数码中没有“10”这个数可以清楚地看出,筹算从一开始就严格遵循十位进制,9位以上的数就要进一位。同一个数字放在百位上就是几百,放在万位上就是几万,这样的计算法在当时是很先进的。但筹算数码中开始没有“零”,遇到“零”就空位,这是很容易发生错误的。“0”这一数学符号的发明应归功于公元6世纪的印度人。
另根据史书的记载和考古材料的发现,我国古代的算筹实际上是一根根同样长短和粗细的小棍子,一般长为13~14 cm,径粗0.2~0.3 cm,多用竹子制成,也有用木头、兽骨、象牙、金属等材料制成的,二百七十几枚为一束,放在一个布袋里,系在腰部随身携带。需要记数和计算的时候,就把它们取出来,放在桌上、炕上或地上都能摆弄。别看这些一根根不起眼的小棍子,在中国数学史上它们却是立有大功的。而它们的发明,同样经历了一个漫长的历史发展过程。
按照中国古代的筹算规则,算筹记数的表示方法为(如图1):个位用纵式,十位用横式,百位再用纵式,千位再用横式,万位再用纵式等,这样从右到左,纵横相间,以此类推,就可以用算筹表示出任意大的自然数了。由于位与位之间的纵横变换,且每一位都有固定的摆法,所以既不会混淆,也不会错位。毫无疑问,这样一种算筹记数法和现代通行的十进位制记数法是完全一致的。
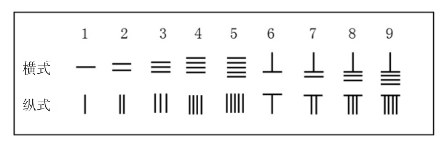
图1 算筹的记数方法
早在两千多年前,我国古代劳动人民就发明了加、减、乘、除的计算方法。不过,当时的方法与现在的不一样,就是用算筹来进行计算的。
如23+73就可以用下面的算筹来计算(如图2):
下面以183×26为例具体说明筹算的乘法(如图3):
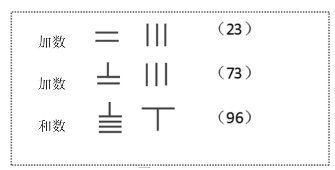
图2 23+73的算筹计算
(1)把乘数26摆在上面,被乘数183摆在下面,被乘数的个位与乘数的十位对齐,中间留有空余,准备摆乘得的积(如图3左上);
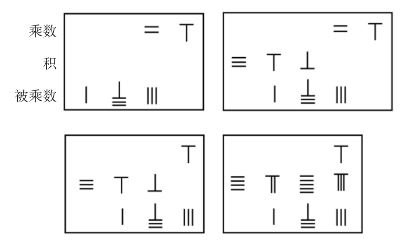
图3 183×26的算筹方法
(2)从高位乘起,用乘数十位上的2乘被乘数183,得3660,摆在中间,积的数位与被乘数对齐(如图3右上,积的个位0用空位表示);
(3)去掉已乘过的乘数十位上的数字2,把乘数个位6移至与被乘数的个位对齐的位置(如图3左下);
(4)用乘数个位6乘被乘数183,所得的积与3660相加,最后得积4758(如图3右下)。
中国古代十进位制的算筹记数法,在世界数学史上是一个伟大的创造。把它与世界其他古老民族的记数法作比较,其优越性是显而易见的。
罗马数字也是最早的数字表示方式,比阿拉伯数字早2000多年,起源于古罗马。古罗马的数字系统没有位值制,只有七个基本符号,如要记稍大一点的数目就相当繁难。
罗马数字是阿拉伯数字传入之前使用的一种数码。罗马数字采用七个罗马字母做数字,即I(1)、X(10)、C(100)、M(1000)、V(5)、L(50)、D(500)。
记数的方法是:
相同的数字连写,所表示的数等于这些数字相加得到的数,如Ⅲ=3;
小的数字在大的数字的右边,所表示的数等于这些数字相加得到的数,如Ⅷ=8、Ⅻ=12;
小的数字(限于Ⅰ、X和C)在大的数字的左边,所表示的数等于大数减小数得到的数,如Ⅳ=4,Ⅸ=9;
在一个数的上面画一条横线,表示这个数增值1000倍,如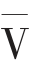 =5000。
=5000。
最常见的罗马数字就是钟表的表盘符号:Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ、Ⅶ、Ⅷ、Ⅸ、Ⅹ、Ⅺ、Ⅻ。对应的阿拉伯数字就是1、2、3、4、5、6、7、8、9、10、11、12。这也就是现在国际通用的数字。
用罗马数字记较大的数非常麻烦,所以现在已不常用了。
古美洲玛雅人虽然懂得位值制,但用的是20进位;古巴比伦人也知道位值制,但用的是60进位。20进位至少需要19个数码,60进位则需要59个数码,这就使记数和运算变得十分繁复,远不如只用9个数码便可表示任意自然数的十进位制来得简捷方便。中国古代数学之所以在计算方面取得许多卓越的成就,在一定程度上应该归功于这一符合十进位制的算筹记数法。马克思在他的《数学手稿》一书中称十进位记数法为“最妙的发明之一”。
除了十进制以外,在数学萌芽的早期,还出现过五进制、二进制、三进制、七进制、八进制、十进制、十六进制、二十进制、六十进制等多种数字进制法。在长期实际生活的应用中,十进制最终占了上风。
现在世界通用的数码1、2、3、4、5、6、7、8、9、0,人们称之为阿拉伯数字。实际上它们是古代印度人最早使用的。后来阿拉伯人把古希腊的数学融进了自己的数学中去,又把这一简便易写的十进制位值记数法传遍了欧洲,逐渐演变成今天的阿拉伯数字。
数的概念、数码的写法和十进制的形成,以及数的运算,都是人类长期实践活动的结果。
随着科学技术的进步,人们认识世界的水平也在不断地提高,大到宇宙太空,小到质子中子,下面就让我们一起感受一下超大数字和超小数字。
先看一个重赏国际象棋发明人的故事。
据说现在的国际象棋是印度人发明的,有一个故事是说这个发明象棋的聪明人,把他的发明献给印度国王,这个“饱食终日”的国王最喜欢可以消遣的东西,因此他命令他的大臣拿珠宝黄金给这个聪明人。这个聪明人却表示他不想要黄金、珠宝,他只要麦粒。他指着面前的棋盘奏道:“陛下,就请您赏给我一些麦子吧,我的要求是第一个格里放一颗,第二个格里放两颗,第三个格里放四颗,以后每一个格里都比前一个格里的麦粒增加一倍。圣明的王啊,只要把这样摆满棋盘上全部六十四格的麦粒都赏给你的仆人,我就心满意足了。”国王听了哈哈大笑,心里想:“有这样蠢的人,好东西不要,却要这么少的几粒麦子。”因此就对大臣说:“给他十袋麦子好了,不必这样麻烦地算。”可是聪明人仍要按他的那个原先要求,不要十袋麦子,国王于是答应他的要求。计算麦粒的工作开始后不久,国王便暗暗叫苦了,因为尽管第一袋麦子放满了将近二十个格子,可是接下去的麦粒数增长得竟是那样的快,国王很快意识到,即使把自己王国内的全部粮食都拿来,也兑现不了他许给聪明人的诺言了!
理由很简单:麦粒数是1+2+4+8+…+263(棋盘共有64格),这是个很大的数字,这数字大得超过恒河沙滩上的沙粒。
这个数实际上是等比数列1,2,4,8,…的前64项的和,即等于264-1。
这是一个二十位的大数,即264-1=18446744073709551615≈1.8×1019。
如果一斤需要26000粒麦粒,把它换算成吨为:
18446744073709551615÷26000÷2000=354745078340.568(吨)
约三千五百亿吨,据说是全世界人民500年的口粮。
264,一个看起来好像不大的数,但是用数学的方法进行计算,其大数的结果却超乎想象,令人惊叹,不可思议。
又如,把一个苹果切成薄片能否覆盖地球的表面?
现实似乎是不可能的,但理论上却是完全可以的,只要切出的薄片的厚度小于10-20厘米就可以实现。但实际情况是无论用什么办法,根本无法切到如此薄的薄片。
古代希腊人曾经提出过一个问题:他们认为世界上的沙子是无穷的,即使不是无穷,也没有一个可以写出来的数超过沙子的数。阿基米德的回答是:不。在《数沙术》中,阿基米德以万为基础,建立新的记数法,使得任何大的数都能表示出来。他的做法是:从1起到1亿叫做第1级数;以亿亿为第2级数的单位,从亿到亿亿叫做第2级数;再以亿亿为单位,直到亿亿亿叫做第3级数等。阿基米德算出充满宇宙的沙子的数目不过是10级数,即使扩充到“恒星宇宙”,即以太阳到恒星的距离为半径的天球,也不过只能容纳10个级数的沙粒!
同样的问题也出现在中国古代。东汉时期的数学专著《数术记遗》中最早记录了中国古代关于对大数的一整套命名和三种进位方法。
《数术记遗》称:黄帝为法,数有十等,及其用也,乃有三焉。十等者,亿、兆、京、垓、秭、壤、沟、涧、正、载。三等者,谓上、中、下也。其下数者,十十变之,若言十万曰亿,十亿曰兆,十兆曰京也。中数者,万万变之,若言万万曰亿、万万亿曰兆,万万兆曰京。上数者,数穷则变,若言万万曰亿,亿亿曰兆,兆兆曰京也。从亿至载,终于大衍。下数浅短,计事则不尽,上数宏阔,世不可用。故其传业,唯以中数耳。
下面的表格就是用中数表示的大数字和小数字的单位:
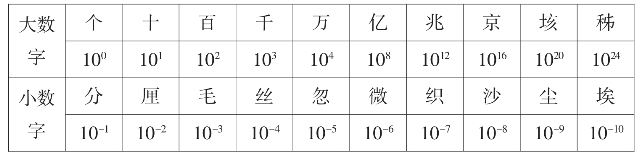
如前面提到的麦粒数18446744073709551615。可读作一千八百四十四京六千七百四十四兆七百三十七亿九百五十五万一千六百一十五。
当然,这样读起来还是很麻烦,所以超大数字或超小数字还是用现代科学计数法比较方便。下面给出一些超大(或超小)数字,仅供参考。
地球的质量是:5.965×1024千克;
铂原子的质量是:4×10-26千克;
人的平均寿命是:2.2×109秒;
长城的年龄大约为:7×1010秒;
光波的周期大约是:2×10-15秒;
地球到太阳的距离约是:1.5×1011米;
一光年是:9.5×1015米;
原子的半径大约为:1.0×10-10米。
一个时代人们对于数的认识与应用,以及数系理论的完善程度,反映了当时数学发展的水平。数的概念的每一次扩充都标志着数学的巨大飞跃,今天,我们所应用的数系,已经构造得如此完备和缜密,以致于在科学技术和社会生活的一切领域中,它都成为基本的语言和不可或缺的工具。但是,当数学的思想一旦冲破传统模式的藩篱,便会产生无可估量的创造力,未来的数学等着你。
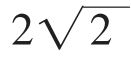 的一个向量了。
的一个向量了。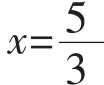 ,这是引进分数的必要;
,这是引进分数的必要;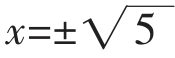 ,这是引进无理数的必要;
,这是引进无理数的必要;


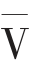 =5000。
=5000。