-
1.1前言
-
1.2目录
-
1.31 绪 论
-
1.3.11.1 引言
-
1.3.21.2 无网格法的研究进展
-
1.3.31.3 对无网格法的粗浅认识
-
1.42 无网格法的近似函数
-
1.4.12.1 移动最小二乘(MLS)近似
-
1.4.1.12.1.1 MLS形函数
-
1.4.1.22.1.2 权函数与支持域
-
1.4.1.32.1.3 MLS形函数的特点
-
1.4.1.42.1.4 MLS形函数的MATLAB程序
-
1.4.22.2 径向基点插值近似函数
-
1.4.2.12.2.1 RPIM近似函数
-
1.4.2.22.2.2 RPIM形函数的性质
-
1.4.2.32.2.3 RPIM近似函数的MATLAB程序
-
1.53 弹性静力学问题的无网格法
-
1.5.13.1 弹性力学的基本方程和边界条件
-
1.5.1.13.1.1 弹性力学基本假设
-
1.5.1.23.1.2 重要的物理量
-
1.5.1.33.1.3 平衡方程
-
1.5.1.43.1.4 物理方程(本构方程)
-
1.5.1.53.1.5 应变能、余能和总位能
-
1.5.23.2 无网格Galerkin法(EFGM)
-
1.5.2.13.2.1 含拉格朗日乘子的EFGM 公式
-
1.5.2.23.2.2 含罚函数的EFGM 公式
-
1.5.2.33.2.3 积分方案
-
1.5.2.43.2.4 EFGM 的计算流程
-
1.5.33.3 径向基点插值法(RPIM)
-
1.5.43.4 光滑无网格Galerkin法
-
1.5.4.13.4.1 光滑应变
-
1.5.4.23.4.2 系统离散方程
-
1.5.4.33.4.3 施加边界条件
-
1.5.4.43.4.4 两层嵌套光滑积分网格
-
1.5.4.53.4.5 数值算例
-
1.5.53.5 EFGM的MATLAB程序
-
1.64 弹性动力学问题的无网格法
-
1.6.14.1 改进的MLS近似
-
1.6.24.2 弹性动力学问题的EFGM
-
1.6.34.3 弹性动力学问题的光滑Galerkin无网格法
-
1.6.44.4 自由和受迫振动分析
-
1.6.54.5 数值算例
-
1.6.5.14.5.1 自由振动分析
-
1.6.5.24.5.2 悬臂梁受迫振动分析
-
1.6.64.6 动力学问题中MATLAB程序
-
1.6.6.14.6.1 子空间迭代法
-
1.6.6.24.6.2 Newmark方法的MATLAB程序
-
1.75 线弹性断裂力学问题的无网格法
-
1.7.15.1 线弹性断裂力学
-
1.7.25.2 EFGM中求解断裂问题的几种处理技术
-
1.7.2.15.2.1 权函数修正法
-
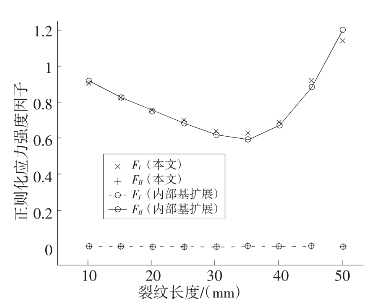
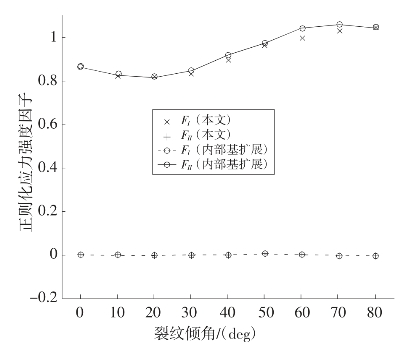
1.7.2.25.2.2 内部基函数扩展
-
1.7.2.35.2.3 外部MLS扩展
-
1.7.2.45.2.4 外部单位分解扩展
-
1.7.35.3 单位分解扩展RPIM求解复合应力强度因子
-
1.7.3.15.3.1 单位分解法
-
1.7.3.25.3.2 单位分解扩展RPIM(X-RPIM)的位移模式
-
1.7.3.35.3.3 控制方程的弱形式及其离散化
-
1.7.3.45.3.4 相互作用积分(M积分)
-
1.7.3.55.3.5 数值算例
-
1.7.3.65.3.6 X-RPIM的MATLAB程序
-
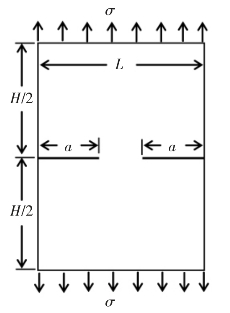
1.7.45.4 模拟多裂纹问题的无网格法
-
1.7.4.15.4.1 多裂纹问题的内部基扩充无网格法
-
1.7.4.25.4.2 多裂纹问题的XFEM
-
1.7.4.35.5.3 数值算例
-
1.86 裂纹扩展的水平集和无网格耦合法
-
1.8.16.1 水平集及其更新算法
-
1.8.1.16.1.1 水平集描述裂纹
-
1.8.1.26.1.2 模拟裂纹扩展的水平集更新算法
-
1.8.26.2 水平集和无网格耦合方法
-
1.8.2.16.2.1 不连续位移模式
-
1.8.2.26.2.2 控制方程的弱形式及其离散化
-
1.8.36.3 裂纹扩展准则及确定新裂纹尖端
-
1.8.3.16.3.1 最大周向应力准则
-
1.8.3.26.3.2 裂纹扩展步长的确定
-
1.8.3.36.3.3 新裂纹尖端坐标的确定
-
1.8.46.4 数值实验
-
1.8.4.16.4.1 应力强度因子的计算
-
1.8.4.26.4.2 裂纹扩展模拟
-
1.97 接触摩擦问题的扩展无网格法分析
-
1.9.17.1 扩展无网格法的不连续位移模式
-
1.9.27.2 基于互补理论的接触问题描述
-
1.9.2.17.2.1 接触面方程
-
1.9.2.27.2.2 接触问题的虚功方程
-
1.9.37.3 无网格离散控制方程及线性互补方法
-
1.9.3.17.3.1 离散控制方程
-
1.9.3.27.3.2 方程求解
-
1.9.47.4 数值算例
-
1.9.4.17.4.1 含贯通节理方板
-
1.9.4.27.4.2 边裂纹受压力作用
-
1.9.4.37.4.3 受压裂纹应力强度因子
-
1.9.57.5 Lemke算法的MATLAB实现
-
1.10参考文献
1
无网格法理论及MATLAB程序