第十章 《逻辑哲学论》中的意义、真和逻辑
本章概要
1.真、意义和图像论
图像类比;原子句通过与原子事实共享抽象的逻辑形式来表现原子事实
没有意义的有意义性
真的原子句对应于真的原子事实;所有的事实都是原子事实;非原子句的真和意义要依据原子句的真和意义而得以解释;知道意义就是知道真值条件
2.维特根斯坦的逻辑系统
对真值函项和一般性的《逻辑哲学论》式的处理
3.维特根斯坦一般性的逻辑原则
所有有意义的句子都是原子句的真值函项
重言式并不陈述必然事实,而是我们符号体系的制品
所有必然性都是逻辑的必然性(重言式),它可以仅仅通过形式而被发现
判定程序(Decision procedures):真值表的方法和命题演算;不存在一种关于《逻辑哲学论》中逻辑的判定程序
可证性:关于这种想法的问题,即所有《逻辑哲学论》中的逻辑真理都是可证的
真、意义和图像论
在上一章中我们谈论了维氏关于形而上学简单物的设想,以及关于它们组合成原子事实的方式。现在我们将转向他关于真、意义、必然性、可能性、可设想性和逻辑的看法。同之前一样,我们从原子句开始。我们被告知,它们是逻辑专名的组合,这些组合描画(picture)或表现了可能事态。在《逻辑哲学论》的体系中,每个名称精确地命名一个对象,这个对象就是该名称的意义,而且每个对象也都精确地被一个名称命名。名称在一个原子句中被放置在一起的方式,表现了被命名的对象可以被组合在一起的方式。原子句(维氏也称其为原子命题)被说成是描画了可能事实或事态,后者可以被当作前者的意义。这里有两样东西值得注意——图像类比和维氏关于意义的设想。
首先是图像类比。它可以通过一对著名的例子来加以阐明。第一个例子是交通事故的庭审模型,在其中玩具车辆表示真正的车辆。在这套模型里,把玩具车辆放置在某种特定的空间排布中,这一点表现了真实车辆的那种排布。在这个例子里,模型的空间属性和关系允许它描画或表现真实车辆的空间属性或关系。第二个例子是关于一座谷仓的具象绘画(representational painting)。在这种情况下,通过把画布上的某个特定部分变成红色,人们可以表现那座被画成红色的谷仓。
那么语言的情况又是如何呢?我们并不用彩色的墨水来表现各种语词所指的颜色。我们一般也不把语词放置在这样的空间关系中:这些关系以直接的、点位式的方式,与我们所谈论的那些项目之间所存在的空间关系相对应。维氏仍然认为,一个原子句具有表现一个可能事实或事态的能力,这仅仅是由于这个句子和事态具有共同的形式。一般而言,这种共同形式不会是一种空间形式——就像交通模型中那样,也不会是一种涉及颜色之类属性的物理形式——就像在谷仓画的情形中那样。因此维氏说,一个原子句和它所描画或表现的事态之间所共有的那种形式必然是一种抽象的逻辑形式(1)。
尽管这项原则看上去十分宏大,我却认为它实则相当简单。根据维氏的看法,一个原子句是一个语言上的事实——一个有特定结构的名称的组合——而一个事态则是一个可能的非语言上的事实——一个有特定结构的对象的组合。为了使语言事实描画或表现可能事态,那些关于名称在句子中的组合方式的事情,必须对应于对象是如何在事态中组合的。一般而言,关于那些事情是什么这一点,并没有太多可以说的。它们仅仅是关于如下这种语言上的约定的事项:将名称组合在一起的特定方式——也就是说,将名称彼此放置在独特的关系中以形成一个句子——表现了可能的事态,在这些事态中,对象被那些处于特定关系中的名称所指涉。例如,在句子Nab(意为a在b的北边)中,名称a处于与名称b的如下关系中:直接-出现在-它-之前-并且-在-这个-符号-N-之后。两个名称在这个关系中的组合表现了如下这点:由a命名的对象处于与由b命名的对象的在-它-的-北边的关系中。在创立一种语言时,人们会采用如下这样的语言上的约定:它们规定不同的专名指涉哪些对象,以及名称间所存在的不同的语言关系指涉对象间存在的哪些非语言关系。当维氏说一个原子句和它所表现的可能的原子事实共享一种逻辑结构时,我认为他全部的意思就是:就像可能的原子事实是这样一种组合——对象在其中处于一种特定的关系Ro中——一样,原子句也是这样一种组合——名称在其中处于一种特定的关系Rn中,而且某种语言上的约定会根据如下之点被采用:关系Rn中名称的哪种配置表现了可能事实中关系Ro里那些被命名为彼此具有关系Ro的对象。(2)
简言之,根据图像论,为了使一个事实能表现另一个事实,这两个事实必须具有共同的形式。有时,就像在交通模型和谷仓的具象绘画中那样,形式涉及特定的物理属性和关系——颜色或空间关系——这些属性和关系是用来进行表现的事实和被表现的事实所共同具有的。在另一些情形下,比如在语言中,在以上所表明的意义上,共同的形式仅仅是一种抽象的逻辑形式。
现在我们转向图像论所建言的其他要点。请考虑一下具象绘画。使得一幅图画成为具象性的东西不是任何它所表现的实际事物的存在;一幅关于独角兽的画可以是具象性的,即使独角兽并不存在。考虑到这点,人们可能以为,使得一幅图画具有具象性的东西在于它表现了一个可以或可能想象为存在的对象或情况,即使这个对象或情况实际上并不存在。接下来,请考虑原子句。我们可以问,什么使得一个原子句有具象性——换言之,是有意义的?一些哲学家可能给出这样的答案:一个原子句的有意义性在于这个事实,即它代表或表达了某物——某个是它意义的实体。早期罗素就是一位这样的哲学家,他认为命题是被这样的句子所表达的抽象对象:这些句子可以被施事者相信或断定。然而,这并不是维氏关于什么使得一个原子句有意义或者其有意义性何在的设想。根据维氏的看法,一个原子句是有意义的或具象性的,仅当这个原子句中被命名的对象可以被按照如下方式排列:这种方式对应于名称在句子中排列的方式。在他看来,我们可以通过说一个原子句的意义是一个可能事实或事态来表达这一点。
但是,他可以补充道,如果我们用这种方式表达自己,那么一定小心不要提供错误的印象。维氏的确不认为,在实际的事实或事态之外还有更多的实体——仅仅可能的事实或事态——它们具有这样一种存在,即缺乏具有充分资格的存在性或现实性。仅仅可能的事实或事态不会被认为是真正的实体。这样看来,当我们说有一些事态仅仅是可能的时,我们的意思是,事情可能与它们的实际所是有所不同。我们并不是说,有这样一种对象的组合,它在实际世界中有一种弱的存在,但却又可能有一种更强的存在。(3)
随之而来的结果是,对那些为假的原子句来说,作为它们意义的事物不存在。这些句子是有意义的,但使其有意义的东西不在于它代表或表达了某种是其意义的实体。相反,一个原子句是有意义的,当且仅当世界中的对象可以以如下方式被排列:这种方式对应于名称在句子中的排列方式。知道一个原子句的意义并不是要去亲知某种抽象实体——一种意义,一个命题或一个可能事态。相反,我们要去知道,如果这个句子是真的,那么世界将会是什么样子。这种想法——一种意义理论不要求意义本身是一种实体,而且理解一个句子就是去知道它在何种情况下为真——迟早会对哲学家和语言理论家产生巨大的影响。值得注意的是,这种想法似乎在《逻辑哲学论》中第一次获得了系统性的发展。
这把我们引向维氏关于真的观点。一个原子句为真,当且仅当它对应于一个原子事实。只有在这种情况下才是如此:在句子中被命名的对象确实以这种方式——它们的名称在句子中被组合的方式所表现的那样——组合在一起。简言之,一个原子句是真的,当且仅当世界中的对象真的如这个句子说它们所是的那样;否则该句子为假。那么非原子句又如何呢?对维氏来说,非原子句的真或假总是由原子句的真或假决定。因此,他看似无需假定非原子事实的存在。例如,请考虑否定句的情况。让我们考虑对原子句Lab的说明(为了论证的方便,我们可以设想这个句子说的是a在b的左边)。该句子的否定~Lab为真,当且仅当原初的句子Lab为假——换言之,当且仅当不存在一个由a之存在于b左边所构成的事实。为了解释这个否定句的真,我们不需要说世界中存在着这样一个对应于这个否定句的事实。相反,它的真在于它不对应任何事实。
实际上,维氏在意义和真的问题上采取了一种两级理论。在级别1上,原子句被说成是代表可能事态的,可能事态的实际存在将使得原子句为真。(4)在级别2上,非原子句的意义和真依据原子句的意义和真而得以解释。不存在这样的可能事态:它由一个真值函项复合句所代表,而且它的实际存在会使得这个句子为真。要知道一个否定句~S的意义就是要知道S的意义,以及什么叫做把否定运算运用于一个句子。否定算子并没有命名世界中的对象,而且当~S为真时,这个句子也没有描画或对应于一个事实。要知道~S的意义,并不是要把它和一个可能事态关联起来。相反,应当把它与S以一种特殊的方式关联起来,在这种方式中S与一个可能事态相关联(如果S是一个原子句的话)。同样的说法可以适用于其他真值函项复合句。
在《逻辑哲学论》所阐发的这幅一般性的图景中,原子事实是所有存在的事实。可能的原子事实的不同组合构成了不同的可能世界(即宇宙可能所是的方式)。任何一个可能世界中都不存在任何超越于该世界中所存在的原子事实之上或之外的东西。我们可以通过这种方式来更清楚地阐明这一点,即从语言的视角来看事物。假设A是一个原子句的集合,而f是对A中每个成员真假的赋值。对A中的每个句子S,f赋予S真或假。A中被f赋值为真的那些句子的集合表现了一个完整的可能世界。如果我们拥有一套不同的赋值f’,那么被f’赋值为真的句子的集合可能表现了一个不同的可能世界。最后,请考虑对A成员的所有可能的赋值——也就是说,诸原子句之间每一种可能的真和假的赋值方式。其中一种方式会赋予每个原子句真,而另一种会赋予每个原子句假,而且对于这两种极端状况间的每一种可能的组合而言,都会存在一种这样的赋值:它将真值的组合给予A中的句子。《逻辑哲学论》的原则坚信:(i)每一种可能的赋值都表现了一个真正可能的世界(一种宇宙真的可以是或可能会是的方式);(ii)每一个可能世界都被一种可能的赋值所表现。
记住这一点之后,请设想S是某种非原子句的情况。既然我们知道不存在非原子事实,我们也就知道S的真或假不可能在于它与一个非原子事实的对应或不对应。相反,S的真或假必定由哪些原子事实存在所决定;或换言之,S的真或假必定由如下这点决定:哪些原子句为真,哪些为假。维氏通过清晰地断言这条很强和意义很深远的原则来表达上述意思:每一个命题(有意义的句子)都是原子命题的一个真值函项。根据这条原则,任何一种对有意义的原子句(命题)集合A中所有成员的赋值,都自动决定了每一个真正命题(有意义的句子)的真值。此外,维氏似乎认为,要知道任何一个逻辑复合句的意义,就是要知道它的真或假是如何通过原子句而被决定的。(5)
这就是一般的图景。接下来我会说说维氏如何填补这些细节:复合句如何依据原子句而得以分析。在此简单回顾一下罗素的方法会很有帮助,那样我们就可以把他和维氏的方法进行对比。
维特根斯坦的逻辑系统
在罗素主义的逻辑中,我们的起点是原子式——例如,Fa和Fx。复合式可以由更简单的式子以如下两种方式构成:(i)我们可以将真值函项算子——~、&、v、→、↔——用于得到诸如(Ga & Hab) v ~(Px→Qy)这样的式子;(ii)我们可以将存在和全称量词算子用于得到诸如∃x Fx和∀x Fx这样的式子。在罗素的逻辑中,有些式子含有两种复合方式——例如,∀x(Fx →Gx)。这个句子由原子式Fx和Gx构成,首先使用了真值函项算子“→”,然后加上了全称量词。这些算子运算的不同顺序会产生不同的结果。如果我们颠倒了这个顺序,首先将全称概括运用于原子句,然后再把这些同真值函项算子“→”相连接以进行条件运算,我们会得到一个不同的和不等值的式子,(∀x Fx→∀xGx)。所以,对罗素而言,复合式是由原子式通过真值函项——~、&、v、→、↔——和量词——∀x、∃x——算子的有限多的运用构建而成的。有些复合句包含两种算子,并且算子用于构建句子的顺序会使得这个句子说出不同的东西。
维氏的逻辑则是被着眼于设计成这样的:它本质上得到了与罗素同样的结果,但方式却不同。首先,维氏将真值函项算子的观念进行了概括。与罗素拥有~、&、v、→、↔不同,维氏只拥有一个算子N,用于连接否定。与罗素的真值函项算子——它们总是被用于一个简单的式子(比如在~S中)或一对式子[比如在(A&B)中]不同,维氏的算子N可以被用于诸多式子——N(A),N(A,B),N (A,B,C)……——以制造这样一个复合式:它为真,当且仅当它被用于的所有式子都是假的。其次,维氏采用了与罗素不同的量词系统。罗素系统中的量词——∀x,∃x——自身不是真值函项算子,而维氏的逻辑则消除了作为独立算子的量词。他的想法是,量词的功能可以被更为概括的算子N所代替,这样一来,从原则上说这种功能甚至可以被运用到无穷的式子集合中。例如,在维氏的系统中,N(Fx)是一个只在这种情况下为真的句子:每一个通过将变量x替换为一个对象的名称(每个名称都对应一个相应的句子)的句子N(Fa)、N(Fb)、N (Fc)……全部为真。简言之,维氏试图发展这样一种系统,在其中每一个真正的命题都可以由简单的原子命题(原子句)和对简单的真值函项算子N的运用来构造。
在《逻辑哲学论》中构建这个体系的时候,维氏并没有完全详细地阐明为了达到他要的结果所需要的全部细节。但是,我们却可以通过在他清楚的评论上进行补充的方式来实现他的设想(6)。接下来便是对这种方案的简要概述。
语言
1.原子式是由n个名称或变量跟随着n项谓词组成的。
2a.如果F1,……,Fn是式子,那么(F1,……,Fn)是一个集合的代表(set representative)。
b.如果G是一个这样的式子:在其中变量v拥有一个自由出现,那么(v[G])是一个集合的代表。
c.除此之外没有集合的代表。
3.如果S是一个集合的代表,那么NS是一个式子。(除此之外没有别的东西是式子。)
4.句子是这样的式子:在其中所有变量的出现都是被约束的。[当一个变量v以(2b)中的那种方式被用于形成一个集合的代表时,它约束了G中v的所有自由出现。以这种方式不受约束的出现是自由的。]
真值条件
1.一个原子句是真的,当且仅当它的谓词适用于其逻辑专名所命名的对象。(请注意,为了使得一个原子式成为一个句子,它不能包含任何变量。)
2.一个句子NS是真的,当且仅当所有对应于集合的代表S的句子都是假的。
3a.如果S=(v[G]),那么一个句子对应于S,当且仅当该句子通过如下方式产生自G:将G中所有的自由出现替换为一个单一名称的出现。
b.如果S=(F1,……,Fn),那么一个句子对应于S当且仅当它是一个Fi’s。
罗素主义的句子及其在《逻辑哲学论》中等价句的例子
~P N(P)
~P& ~Q N(P,Q)
P & Q N(N(P),N(Q))
P v Q N(N(P,Q))
P& ~Q N(N(P),Q)
~(P& ~Q) N(N(N(P),Q))
P →Q N(N(N(P),Q))
~P v Q N(N(N(P),Q))
~∃x Fx N(x[Fx])
∃x Fx N(N(x[Fx]))
~∃x~Fx N(x[N(Fx)])
∀x Fx N(x[N(Fx)])
~∃x (Fx & Gx) N(x[N(N(Fx),N(Gx))])
∃x (Fx & Gx) N(N(x[N(N(Fx),N(Gx))]))
∃x (Fx &~Gx) N(N(x[N(N(Fx),Gx)]))
~∃x (Fx &~Gx) N(x[N(N(Fx),Gx)])
~∃x~(Fx→ Gx) N(x[N(N(Fx),Gx)])
∀x (Fx→ Gx) N(x[N(N(Fx),Gx)])
∀y∃x(Rxy) N(x[N(x[Rxy])])
简要的说明:
“N(y[N(x[Rxy])])”为真当且仅当下面每一项均为假:(i)“N(x[Rxa])”,(ii)“N(x[Rxb])”,(iii)“N(x[Rxc])”,等等,每个句子对应一个对象。情况会是这样的,当且仅当(i)“~∃x Rxa”为假,(ii)“~∃x Rxb”为假,(iii)“~∃x Rxc”为假,等等,每一个陈述对应一个对象。情况会是相反的,当且仅当(i)“~∃x Rxa”为真,(ii)“~∃x Rxb”为真,(iii)“~∃x Rxc”为真,等等,每一个陈述对应一个对象。但情况是这样的,当且仅当对每一个对象y来说∃x Rxy为真——也就是说,当且仅当“∀y∃x(Rxy)”为真。(7)
维特根斯坦一般性的逻辑原则
在这些简要的技术性漫笔之后,现在我们可以回到关于维氏一般逻辑原则的讨论。早先我曾提到,根据《逻辑哲学论》,所有真正的命题——即所有真正有意义的句子——都是原子句(命题)的真值函项。如果是这样,那么任何一种对所有原子命题的赋值都将自动决定所有其他命题的真值。被期望达到这一点的独特方式,涉及对概括的真值函项算子N的重复使用,这与维氏系统的规则是相一致的。(8)为了我们的目标,关于这种构造在特定情况下应当如何运作的细节,往往是无关紧要的。而那些一般原则才是最重要的。
出于这种考虑,我们确定了三条基本的逻辑观念。
• 一个命题S是重言式(逻辑真理)当且仅当所有对原子命题的赋值都使得S为真。(我们会说一个命题是逻辑上必然的当且仅当它是一个重言式。)
• 一个命题S是矛盾式当且仅当任何一种对原子命题的赋值都使得S为假。(我们会说一个命题是逻辑上不可能的当且仅当它是一个矛盾式。)
• 一个命题S是逻辑上偶然的当且仅当S既不是重言式也不是矛盾式。
使用这些观念,我们现在提出了一系列问题。必然性和逻辑必然性之间的关系是什么?不可能性和逻辑上的不可能性的关系是什么?偶然性和逻辑上的偶然性的关系又是什么?
我们可以通过回顾维氏关于原子命题和可能世界(换言之,宇宙可能是或可能会是的方式)的基本假定来回答这些问题。
A1.原子命题是偶然的(在一些可能世界中为真,在另一些中为假)。
A2.任意一个原子命题均独立于其他原子命题;无论其他原子命题的真值如何它都有可能为真(或为假)。
A3.一个可能世界,不会是可能的原子事实的一个集合之上或之外的东西。
从这些假定可以得出,所有对原子命题的赋值都决定了一个可能世界,而且每一个可能世界都对应某种对原子命题的赋值。事实上,在对原子命题集合中的成员进行的赋值和真正的可能世界——也即宇宙可能是或可能会是的方式——之间存在着一一对应的关系。这为我们之前的问题提供了答案。
• 一个命题S是必然的——也就是说,在无论宇宙可以处于哪种状态下S都可以为真的意义上,S在所有可能世界中都为真——当且仅当S是逻辑上必然的(而且因此S是重言式)。
• 一个命题S是不可能的——也就是说,在无论宇宙可以处于哪种状态下S都可以为假的意义上,S在所有可能世界中都为假——当且仅当S是逻辑上不可能的(而且因此S是矛盾式)。
• 一个命题是偶然的——也就是说,在宇宙可以处于某种特定的可能状态下S可以为真而在另一些状态下S为假的意义上,S在某些可能世界中为真而在另一些中为假——当且仅当S是逻辑上偶然的。
在维氏看来,逻辑上必然的命题和逻辑上不可能的命题在某种意义上是退化的(degenerate)命题。通过进一步考察重言式我们可以看到这意味着什么。既然这些句子在所有可能世界中为真,它们不会向我们提供任何关于这个世界的实际状态的信息,这些信息把这种实际状态同该世界其他可能的状态区别开来。因此,在某种意义上,它们向我们提供的不是关于事情是怎样的信息,而是关于事情可以是怎样的。这使得维氏声称它们没有说出任何事情。重言式仅仅是拥有一个包含真值函项算子的符号系统的结果。人们需要真值函项以说出如下事情:世界不是如此这般的,和世界是如此这般的或如此那般的。然而一旦你拥有了真值函项算子,重言式就以某些与它们伴随在一起的可容许的方式而得出了。
在维氏看来,重言式的真不应被归因于必然事实的存在。世界中不存在与重言式相对应的必然事实。重言式不过就是我们符号体系的制品。例如,当你认出(A v ~ A)和((A & (A→B))→B)是重言式时,你并没有把握住某些形而上学意义上的必然事实;你只是看到了一些关于真值函项算子如何工作的事情。在上述第二条重言式的情形下,人们可能通过说出如下东西来表达这一点:当你把握住这个重言式时,你看到了我们的符号使用是这样的,即B得自A和(A→B)。当然,重言式并没有说出这些;它并没有说“我们的符号体系是这样的,即B得自式子A和(A→B)”。根据维氏的看法,重言式自身并没有说出任何东西。但是,它作为重言式的地位应当被归因于它所显示的关于真值函项的符号如何工作的东西。(9)
既然重言式是符号使用的产物,那么如果人们总是通过观察一个命题是如何被符号化的便可以辨别它是否是重言式,这将是非常诱人的。维氏认为人们总是可以做到这点。这把我们带向《逻辑哲学论》的如下原则,即逻辑必然性总是可以仅仅被形式决定。为了理解这条原则,我们需要更小心地考虑维氏的意思。
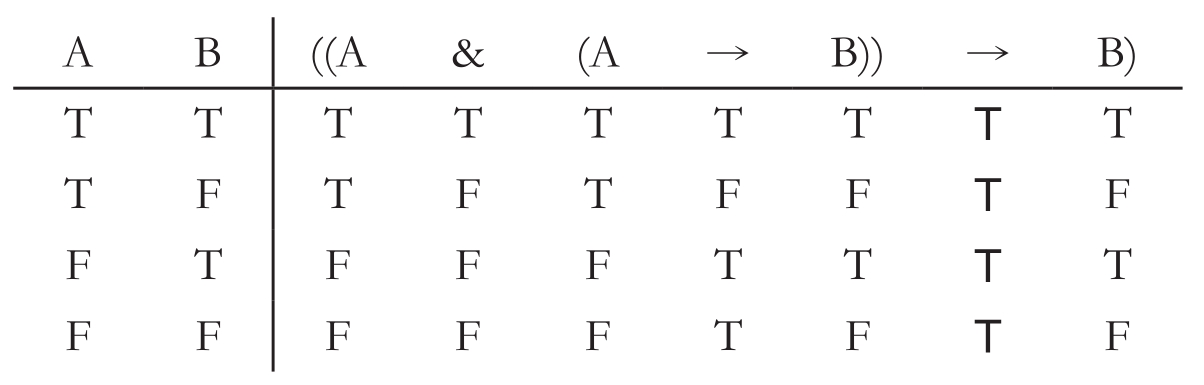
他的一种意思可能是,存在着纯粹机械的判定程序,当这种程序被用于任意一个命题时,它总是会告诉我们(在有限数量的步骤后)一个命题是否为重言式。事实上,维氏用作其原初模型的逻辑系统——即命题演算——现在恰恰具有这种性质。它是这样一种逻辑系统,在其中每一个命题要么是原子命题,要么是将诸真值函项算子有限多地运用于有限多的原子命题所得到的结果。在此不存在量词或其他表达命题演算中一般性的方式。相反,所有的式子要么是代表单独句子的字母(原子命题),要么是有限多的式子通过真值函项算子的有限多的运用而构造出的。例如,句子((A &(A→B))→B)是两个原子命题A和B通过真值函项算子的三次运用而构造出的。所有这种关于演算的命题都是如此的。
可以告诉我们这个或其他命题演算命题是否为重言式的最简单和最自然的判定程序,被称作真值表方法。它可以通过下面的真值表来加以说明。
表中的每一行代表对式子中两个原子命题的一种可能的赋值。既然存在四种赋值,那么这张表就有四行。每一行上的真值都是整个式子的子式的真值,它们得自每一行左侧A和B的赋值。真值函项复合式的真值被列在被用于构建式子——它们由自己的各个部分组成——的真值函项连接词的下方。式子的主要的真值函项连接词是第二次出现的“→”。(这个式子作为一个整体是一个条件式,其后件是B而前件是(A&(A→B))。)每一行里主要连接词下加粗的真值给出了整个式子的真值,这个式子是由每行左侧原子式的赋值所决定的。既然每一行上主要连接词下的真值都是T,那么整个式子在其包含的原子命题的所有可能赋值下都是真的。因此,它是一个重言式。它的真假是某种逻辑上的事项,因为无论它原子部分的赋值如何,作为整体的式子都为真。这种方法适用于所有关于命题演算的命题。在将它用于任意一个给定的句子S时,人们只需写出S的真值表。完成以后,人们观察每一行的主要连接词下的值是否都是T。如果答案是肯定的,那么S就是重言式。反之则不是。
《逻辑哲学论》中的逻辑系统在某种意义上像命题演算,某种意义上又不像。像的方面在于,每一个命题(在某种意义上)都是原子命题的真值函项。不像的方面则在于以下两个方面。首先,在命题演算中,每一个句子都是有限多的原子命题的真值函项。在《逻辑哲学论中》,有一些句子——实际上是任何包含变量的句子——是原子命题的潜无穷的真值函项。其次,在命题演算中,每一个句子都是通过如下方式构成的:将充其量有限多的真值函项算子运用于体系中的其他句子。但是,在《逻辑哲学论》的体系中,有一些句子,例如N(y[N(x[Rxy])])和N(x[N(N(Fx),N(Gx))]),涉及真值函项算子N在其他句子上潜无穷的运用。比如,请考虑N(y[N(x[Rxy])])这个句子。它得自将N运用于潜无穷的句子:(i)“N(x[Rxa])”,(ii)“N (x[Rxb])”,(iii)“N(x[Rxc])”,等等,直到我们为潜无穷的对象a,b,c,d,e,……中的每一个都列出这样的一个句子。此外,这一点对该序列中的每一项又都为真。比如,(i)“N(x[Rxa])”得自将N运用于潜无穷的陈述“Raa”,“Rba”,“Rca”,“Rda”,等等。因此,最初的句子N(y[N(x[Rxy])])得自将N运用于潜无穷的诸命题,这些命题又得自将N运用于潜无穷的诸命题。显然,我们不可能写出这样一个句子的真值表。
因此,真值表方法并不总能适用于《逻辑哲学论》体系中的句子。然而,维氏似乎认为他的体系足够类似于命题演算,以至于我们可以为它构造一个判定程序。他似乎认为,他的系统中的一个句子是否为重言式,这一点原则上可以通过机械的方式被决定。但是,这样一来他就错了。在《逻辑哲学论》完成十多年后,数学家兼哲学家阿伦佐·邱奇(Alonzo Church)证明了,对于标准的罗素主义逻辑系统来说,不可能存在一种决定逻辑真理的形式上的判定程序,甚至对下述任何一种体系来说都是如此:人们试图通过在该体系中加入量词、多元变量、二元或更高阶的谓词的全部力量来超越命题演算——就像罗素主义逻辑那样;或者,同样地,通过允许句子成为无限多的真值函项算子在无限多的原子句上的运用所产生的结果来超越命题演算——就像《逻辑哲学论》的逻辑系统那样。所以,如果维氏设想自己的原则——所有的逻辑必然性都仅仅通过形式而被决定——是:存在一种形式上的判定程序来确定他的理想逻辑语言中任意一个句子是否是逻辑真的,那么显然他恰恰错了。(10)
但是,关于这种原则有一种较弱的解释,即所有的逻辑必然性均通过形式自身决定,这种解释自身值得进行检验。这种解释建基于关于标准的罗素主义逻辑的另一条数学定理,它在《逻辑哲学论》后约十年被库尔特·哥德尔证明。这条定理表述如下:“对于标准罗素主义系统中的逻辑真理,存在一个可靠的、完全的、积极有效的检测。”也就是说,存在一个具有如下特征的纯然机械的测试:(i)无论你何时提供给它一个是逻辑真理的句子,它都会在有限数量的步骤后正确地告诉你该句子是逻辑真理;(ii)无论你何时提供给它一个不是逻辑真理的句子,它或者会正确地告诉你该句子不是逻辑真理,或者永远工作下去而不告诉你任何东西。另一种表达这些的方式如下:任何一个罗素主义的逻辑真理,都可以单独地在其逻辑形式的基础上经过有限数量的步骤而得以证明。然而,如果你尝试证明一个句子却没有成功,那么不存在一种一般性的方法去知道你是否能够在稍后证明它,或者它是否根本无法证明。
既然我们已经展示了罗素的真值函项和量词算子可以与维氏体系中的这些东西相关联,那么设想上述重要的逻辑结果可以推广到维氏的体系中,也就是自然而然的了。虽然在某种意义上说这诚然是正确的,但还是有一种小故障值得注意。标准的罗素主义逻辑真理和维特根斯坦主义的逻辑真理在定义上有些许不同。
一个句子是罗素主义逻辑真理,当且仅当无论它的名称指涉什么,无论它的谓词适用于什么,无论哪些对象被选为其量词的取值范围,它都为真。
一个句子是《逻辑哲学论》系统中的逻辑真理,当且仅当它在所有可能的《逻辑哲学论》式的事态里都为真——也就是说,在基本的形而上学简单物以任意方式组合于其中的事态里。这等价于如下主张:一个《逻辑哲学论》系统中的句子为真,当且仅当无论它的谓词适用于形而上学简单物的何种组合,无论它的逻辑专名指涉哪些形而上学简单物——假如每个名称都指涉一个简单物而且每个简单物都具有一个名称——它都为真。(我们也遵循维氏的设想,即语言中不存在关于同一性的谓词。接下来还会有关于这一点的更多内容。)
《逻辑哲学论》式的逻辑真理的定义与罗素主义的逻辑真理的定义是同构的,除了下面这个重要特征。在《逻辑哲学论》体系中我们拥有一个固定的对象域——形而上学简单物——它们通过所有可能的《逻辑哲学论》式的事态而得以表现。在罗素主义系统中我们却没有这些。无论何种对象域被选为其量词的取值范围,罗素主义的逻辑真理都必须为真。相反,在涉及一个固定对象域——也就是说实际上的形而上学简单物的集合——的每一种解释下,维特根斯坦主义的逻辑真理都为真,无论这些对象最终说来是什么。
这意味着,所有罗素主义的逻辑真理都是《逻辑哲学论》式的逻辑真理。但严格来说,有些《逻辑哲学论》式的逻辑真理可能并不是罗素主义的逻辑真理——即如下这样的句子,它们在关于量词域由所有实际上存在的对象组成的所有解释中为真,但在关于其他域的某些解释中为假。因此,正如我们所知的那样,所有罗素主义的逻辑真理仅仅基于它们的形式自身都是可证的,即便并非所有《逻辑哲学论》式的逻辑真理都如此。
实际上,我们有理由认为这种可能性是可以被证明的。对任一个数目n,我们可以构造这样一个句子:它在所有至少拥有n个对象的解释中为真。
L.∃x ∃y (x≠y),∃x ∃y ∃z (x≠y & x≠z & y≠z),……
既然在罗素主义系统中,量词域可以是任意大小,那么上述列表中的句子没有一个是罗素主义的逻辑真理。但是,既然在维特根斯坦主义系统中,所有的域都包括同样的形而上学简单物并因而具有同样的大小,那么就存在着如下这样一种危险:很多这样的句子最终会被划归到《逻辑哲学论》式逻辑真理的名下。为了说明这一点,我们这样来推理:设想存在至少两个基本的形而上学简单物。那么这些简单物将存在于所有可能的《逻辑哲学论》式的事态中。上述列表中的第一个句子将在所有这样的事态中为真,因为它说存在着至少两个对象。因此,它会被确定为《逻辑哲学论》式的重言式或逻辑真理。同样,设想存在至少三个基本的形而上学简单物。那么它们将在所有可能的《逻辑哲学论》式的事态中存在,而且因此上述列表中的前两个句子都将被确定为《逻辑哲学论》式的逻辑真理。同样的推理适用于任何数目n。因此,无论实际的形而上简单物最终说来是什么,上述列表中在这个数目之前——包括这个数目——的所有句子都是《逻辑哲学论》式的重言式。但可以肯定的是,不存在这样一种令人感兴趣的意义:那些句子的真值可以在此种意义上通过检查它们的形式自身来确定。(11)
因此,关于维氏原则——所有的必然性都是逻辑必然性,后者总是通过形式自身而被决定的——的解释,我们就有了这样一个看似为真的问题。然而,首先,在此存在着一项缓冲因素,有可能避免该问题出现。在写作《逻辑哲学论》的时代,维氏认为同一性不应被表达为谓词。相反,他接受了这种传统,即不同的变量应当代表不同的对象,就像不同的名称代表不同的对象那样。尽管这项主题涉及一些我们无需深入的困境,但下面的段落还是给出了大致的意思。
5.53 一个对象的同一性我通过一个符号的同一性,而不是借助于同一性符号,来表达。诸对象的不同性我通过诸符号的不同性来表达。
5.5301 显而易见,同一性绝对不是存在于诸对象间的一种关系……
5.5303 顺便说一下:就两个物说它们是同一的,这是胡说,就一个物说它与自身同一,这等于什么也没有说。
5.531 因此,我不写“F(a,b) & a=b”,而写“F(a,a)”(或者“F(b,b)”)。不写“F(a,b) & ~ a=b”,而写“F(a,b)”。(12)
5.532 类似地:不写“(∃x,y)[F(x,y) &x=y]”,而写“(∃x) F(x,x)”;不写“(∃x,y)[F(x,y)&~x=y]”,而写“(∃x,y) F(x,y)”。(13)
5.5321 因此,我们不写“∀x(Fx→x=a)”,而写,比如“[(∃x)Fx→Fa & ~ (∃x,y)(Fx & Fy))]”。“恰好有一个x满足F( )”这个命题便成为:“[(∃x)Fx &~ (∃x,y) (Fx & Fy)]”。(14)
5.533 因此,同一性符号并不是概念文字中具有本质意义的部分。
5.534 现在我们看到,在一个正确的概念文字中,诸如“a=a”,“(a=b & b=c)→a=c”,“∀x(x=x)”,“∃x(x=a)”之类的似是而非的命题甚至都不能写出来。(15)
5.535 与这些似是而非的命题联系在一起的所有问题也就因此而自行消解了……
通过排除同一性谓词,维氏排除了L中所列的句子,它们中的每一个说出了诸如存在至少n个对象之类的事情。在做这些的时候,维氏似乎挽救了自己的原则,即所有的逻辑真理都是通过形式自身而得以决定的(在我们所考虑的解释之下)。(16)当然,如果在语言中这些句子是被允许的,那么他们中的很多将最终是《逻辑哲学论》式的重言式,即使不存在这样一种合理的意义:在该意义上关于它们的事实将通过它们的形式自身而被决定。
但这种印象似乎是错误的。既然维氏的原则是不同的名称和不同的变量代表不同的对象,那么人们可以在《逻辑哲学论》系统中构建这样一些句子,它们向维氏的原则提出了如L中所列的句子同样的问题。例如,请考虑新的列表L*,在其中句子被理解为同维氏的如下格言相一致:一个句子中的不同变量代表不同的对象。(17)
L*.∃x ∃y (R2xy v~R2xy),∃x∃y∃z (R3xyz v ~ R3xyz),……
列表中的第一个句子在所有至少存在两个简单物的《逻辑哲学论》式的世界中都为真。第二个句子在所有至少存在三个简单物的《逻辑哲学论》式的世界中都为真,就像在L中那样,以此类推。因此,维氏的原则——所有必然性都是逻辑必然性的原则,以及所有的逻辑真理都通过逻辑自身而被决定——在任何一种他所意图的意义上都不能得到支持。事实上,我们这里所见到的似乎是以下两者之间的冲突:维氏关于形而上学原子论的原则,以及关于所有必然真理的逻辑和语言来源的原则。
这是非常重要的,因为很多哲学家认为,维氏关于如下两个方面之间关系的设想具有引人注目的简单性和合理性:一方面是关于必然性和可能性的形而上学观念,另一方面是关于重言式(逻辑必然性)和一致性(逻辑可能性)的逻辑观念;而上述冲突威胁到了这一点。维氏的设想被概括在《逻辑哲学论》的以下三条原则里:
(i)在如下意义上所有必然性都是语言必然性:它是我们关于世界的表现体系的结果,而非这个世界自身的结果。存在着必然真的句子或命题,但不存在与之相对应的必然事实。相反,它们的必然性应当被归因于语词的意义(因此是先天可知的)。
(ii)所有的语言必然性都是逻辑必然性。
(iii)所有的逻辑必然性都通过形式自身而被决定。
其中的第一条原则,即所有必然性都是语言必然性,在接下来约五十年的时间里主宰了关于这个话题的哲学思考,并对那个时代兴旺发达的观念——把哲学作为语言分析——至关重要。后两条原则,尽管不是没有影响,但很快便被发现具有潜在的问题。
(1) 关于图像论的进一步讨论,请参阅罗伯特·福格林(Robert Fogelin)所著Wittgenstein一书的第二章。
(2) 感谢鲍里斯·柯门特(Boris Kment)对这一点以及其他相关事宜的洞察。
(3) 这种说话的方式似乎承认了“事物(比如宇宙)可能是其所是的诸种方式”和“对象可能被组合的诸种方式”的存在,这些方式自身可以说是某种实体——世界的可能状态(有时被误导性地称为“可能世界”),以及可能事态(“可能事实”)。维氏看似否定这些事物真的存在,尽管上述要点趋向于削弱这种否定,他却并未贯彻这个要点。相反,他似乎更倾向于谈论这种方式,而没有承认其中显而易见的本体论承诺。
(4) 是否存在仅仅可能的事态?这里我们有一个在之前脚注中讨论过的例子,关于维特根斯坦主义对此问题的两可倾向。
(5) 沿着此路前进的人们应当注意避免如下两个值得注意的陷阱。首先,如果理解意义就是通过关于真值条件的知识来进行解释,那么关于真的观念自身就不能预设意义,而且“S”是真的所做出的断言就不能被等同于——或微不足道或明显地等价于——S自身所做出的断言;否则人们就会得出如下荒谬的结论,即人们知道雪是白的当且仅当雪是白的对于如下这两点是充分的:知道雪是白的为真当且仅当雪是白的,知道“雪是白的”的真值条件及其意义。其次,真值函项连接词自身不能依据真和假而被定义,因为任何一种这样的定义——例如~S是真的当且仅当S不是真的——最终会预设一个或更多需要被定义的连接词。因此,至少有一些真值函项连接词必须是初始项。维氏自己是否避免了这些错误,还并不清楚。
(6) 请参阅S. Soames, “Generality, Truth Functions, and Expressive Capacity in the Tractatus,”Philosophical Review 92:4(1983),573—589。
(7) 值得注意的是,罗素主义的带量词的句子及其维特根斯坦主义的对应者在如下意义上是逻辑上等价的:它们在每一个域都具有相同的真值。但是,这两种系统间还是有一些差别,罗素主义逻辑依据在所有可能域中的真来定义逻辑真理和逻辑后承等逻辑观念,而无论域的大小如何;《逻辑哲学论》的系统则预设了一个固定的域。这将导致我们随后会讨论到的一些重要的差别。
(8) 更多内容请参阅“Generality, Truth Functions, and Expressive Capacity in the Tractatus,”pp. 585—588。
(9) 这里我使用从心理学上说更简单的罗素主义——而非《逻辑哲学论》式——的符号来阐明维氏一般性的逻辑要点。接下来我将继续这样做,除非某个关键要点依赖于维氏独特的符号。
(10) 有一种关于这个问题的争论,它因为下述事实而变得更加复杂:尽管维氏似乎意图使用标准的罗素主义逻辑的全部力量来概述一个体系,但《逻辑哲学论》中明确提供的关于变量和一般性的细节仅仅对于如下这样一种体系来说才是充分的,即一种在表达上比标准的罗素系统弱得多的体系。对此主要有两种回应。一是罗伯特·福格林(Robert Fogelin)在《维特根斯坦》一书的第二版第六章中做出的捍卫,即将维氏解释为只承认一种较弱的系统,该系统允许一种关于逻辑真理的形式上的判定程序。二是由彼得·吉奇(Peter Geach)(见于“Wittgenstein’s Operator‘ N’”,Analysis 41[1981],以及“More on Wittgenstein’s Operator‘ N’”,Analysis 42 [1982])和我(见于“Generality,Truth Functions,and Expressive Capacity in the Tractatus”,尤其是第三和第四部分)独立提倡的,主张维氏应当被视作用上文中所展示的力量发展出一种系统。尽管事实上他并没有填补所有的细节,但他关于一般性和算子“N”的描述是与上述处理方法相一致的,我相信,我们需要这种处理方法来克服那些加诸表现性的力量之上的荒谬的限制——特别是当人们记得这个系统意图表达所有有意义的命题的时候。(例如,如果没有填补这些细节,那么人们不可能表达《逻辑哲学论》系统中诸如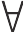 y
y  x(Rxy),
x(Rxy), x(Fx & Gx)甚至
x(Fx & Gx)甚至 x~Fx这样的简单句子。)尽管这种解释使得维氏容易受到如下批评,即他错误地认为自己的系统是可判定的,但他的错误是可以理解的,毕竟那时邱奇的定理尚未被证明,而且从写作《逻辑哲学论》时代的视角来看,他的错误也是革命性的。
x~Fx这样的简单句子。)尽管这种解释使得维氏容易受到如下批评,即他错误地认为自己的系统是可判定的,但他的错误是可以理解的,毕竟那时邱奇的定理尚未被证明,而且从写作《逻辑哲学论》时代的视角来看,他的错误也是革命性的。
(11) 当然,在此可能有这样一种谕告,它根植于那种对重言式可靠的、完全的、积极有效的测试——这种测试仅仅列举出对象的数目,但此种谕告在认识论上对我们是无用的,因为我们无法将告诉我们真理的谕告和告知我们谬误的谕告区别开来。
(12) 译者注:维氏原文如下:“因此,我不写‘f(a,b). a=b’,而写‘f(a,a)’(或者‘f(b,b)’)。不写‘f(a,b). ~ a=b’,而写‘f(a,b)’。符号与本书有所不同,以下亦然。
(13) 译者注:维氏原文如下:“类似地:不写‘(∃x,y) . f(x,y) . x=y’,而写‘(∃x) . f(x,x)’。不写‘(∃x,y) . f(x,y) . ~ x=y’,而写‘(∃x,y) . f(x,y)’。
(14) 译者注:维氏原文为两段话,如下:“因此,我们不写‘(x) : fx x=a’,而写,比如‘(∃x) .fx .
x=a’,而写,比如‘(∃x) .fx . . fa : ~(∃x,y) . fx .fy’。‘恰好有一个x满足f( )’这个命题便成为:‘(∃x) .fx : ~(∃x,y) . fx .fy’”。
. fa : ~(∃x,y) . fx .fy’。‘恰好有一个x满足f( )’这个命题便成为:‘(∃x) .fx : ~(∃x,y) . fx .fy’”。
(15) 译者注:维氏本人使用的符号为:“a=a”,“a=b. b=c. a=c”,“(x). x=x”,“(∃x). x=a”。
a=c”,“(x). x=x”,“(∃x). x=a”。
(16) 在做这些时,他同样通过式子a=b和b≠c的真从可能的反例面前挽救了自己的原则,因为《逻辑哲学论》的原则似乎可以被认为具有如下结果,即如果这些式子为真,则它们必然为真——即使它们的真不能通过它们的形式自身被发现。就这一点而言,值得注意的是,a=b,b=c,a=c,它们在任何情况下都不满足《逻辑哲学论》对原子命题的限制,因为最后一个命题的假与前两个命题的真不相容。如我们所看到的那样,任何原子命题的真或假都与任何另一个原子命题的真或假相容,这是《逻辑哲学论》的一条原则。所以,它们不可能全是原子命题;而如果它们中有一个不是,那么当然就都不是。
(17) 从这个列表中可以得出同样的结果:∃x∃y [(Ax v ~ Ax) & (Ay v ~ Ay)],∃x∃y ∃z[(Ax v ~ Ax) & (Ay v ~ Ay) & (Az v ~ Az)],……
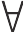 y
y  x(Rxy),
x(Rxy), x(Fx & Gx)甚至
x(Fx & Gx)甚至 x~Fx这样的简单句子。)尽管这种解释使得维氏容易受到如下批评,即他错误地认为自己的系统是可判定的,但他的错误是可以理解的,毕竟那时邱奇的定理尚未被证明,而且从写作《逻辑哲学论》时代的视角来看,他的错误也是革命性的。
x~Fx这样的简单句子。)尽管这种解释使得维氏容易受到如下批评,即他错误地认为自己的系统是可判定的,但他的错误是可以理解的,毕竟那时邱奇的定理尚未被证明,而且从写作《逻辑哲学论》时代的视角来看,他的错误也是革命性的。 x=a’,而写,比如‘(∃x) .fx .
x=a’,而写,比如‘(∃x) .fx . . fa : ~(∃x,y) . fx .fy’。‘恰好有一个x满足f( )’这个命题便成为:‘(∃x) .fx : ~(∃x,y) . fx .fy’”。
. fa : ~(∃x,y) . fx .fy’。‘恰好有一个x满足f( )’这个命题便成为:‘(∃x) .fx : ~(∃x,y) . fx .fy’”。 a=c”,“(x). x=x”,“(∃x). x=a”。
a=c”,“(x). x=x”,“(∃x). x=a”。