第六章 逻辑和数学：逻辑主义还原
本章概要
1．逻辑主义计划导论
古典逻辑主义的目标和动机
2．算术系统
初始项（Primitive terms）和公理
3．罗素的逻辑系统
内涵公理模式（the axiom schema of comprehension），以及关于外延和无限的公理
4．将算术还原为逻辑
算术初始项（primitives）的定义，以及从罗素逻辑系统中对算术公理的推导
5．罗素悖论和类型理论
罗素的逻辑系统何以必须被修正以避免矛盾；这些修正对逻辑主义计划成功的影响
6．逻辑主义的哲学重要性
逻辑主义计划导论
在发展自己摹状词理论的时候，罗素将逻辑形式与语法形式区别开来，并使用该区分解决了哲学难题，这些难题产生自关于意义的成问题的观点。他的摹状词理论被当作分析的典范，而该理论的成功极大地推动了如下观点：逻辑和概念分析在哲学中是通向进步的道路。这种观点得到了他下一项主要成就额外的有力支持——将数学还原为逻辑的逻辑主义工程的竣工，这呈现在他的伟大著作《数学原理》中，该著作系与阿尔弗雷德·诺斯·怀特海合写，出版于1910年。(1)这种逻辑主义工程可以被分为两个部分——将高等数学还原为算术，以及将算术还原为逻辑。罗素的主要贡献是第一种还原。当两种还原都完成时，最终的结果大致是，将所有初等和高等数学的经典理论还原为这样一个系统，该系统可以被多数人当作一套纯逻辑的理论。
为了理解这项工程，必须理解什么是数学或逻辑理论，以及将这样一种理论还原为另一种意味着什么。人们可能认为，一种理论就是一组句子的集合，其中每个句子都是某个特定的公理集合的逻辑后承。这些公理表达如下命题：它们为支持该理论的人所假定，且无需证明就被接受。理论中的定理，构成可以从公理中得到证明的全体陈述。既然它们都在逻辑上得自公理，那么如果公理为真，则它们也必定为真。
公理包含该理论的初始词汇（primitive vocabulary）。它们是这样的语词或符号：这些语词或符号，表达那些无需定义就为我们所熟悉的概念。公理自身是该理论中无需证明就被接受的初始句子，同样，在公理中被使用的词汇，也是那些我们无需定义就知道其意义的初始符号。除了一个理论中的公理之外，我们有时还有一类被称作该理论中定义的句子。它们定义了新的术语，这些术语并不借助那些出现在公理中的初始符号而出现在公理之中。
例如，在很多理论中并没有关于定冠词这个的初始符号，它被用于形式化地表述单称限定摹状词。不过，在使用相应的理论进行工作时，拥有这种使摹状词形式化的能力是很方便的，这时常可以作为避免该理论的句子过长或是在心理上难以处理的手段。因此，摹状词算子有时通过如下定义被引入：
在Ψ是任何（简单的）原子谓词以及Φ是任何式子的地方，Ψ the x：Φx≡∃x ∀y［（Φy↔y=x）& Ψx］
当限定摹状词算子以这种方式被引入后，其结果是，即使公理中不包含限定摹状词，该理论的一些定理中也会包含它们。在这种情况下，该理论的定理被认为是：公理的逻辑后承加上该理论中的这些定义。一般而言，我们会认为，一种理论涉及一组无需证明即被接受的公理，在某些情况下加上一组规定性的定义，这些定义依据理论中的初始词汇确定新的术语。定理就是公理的逻辑后承加上这些定义。
我们现在转向理论还原的概念。假设我们有两种理论T1和T2。将T2还原为T1，就是要做两件事情。第一，将一组规定性定义形式化地表述出来，这些规定性定义依据T1中的词汇将T2中的初始词汇加以定义。换句话说，人们拿过出现在T2公理中的那些词项——它们的意义仅仅是从T2的视角被设想的或想当然地当作那样的——并通过T1的词汇来为那些词项提供定义。第二，人们展示T2的公理如何可以从T1的公理加上被采纳的规定性定义而得到证明。最终的结果是，T2的概念依据T1的概念而被加以分析，而那些未加证明就被接受的公理，现在通过从更为基础的假定证明自己，进而获得了严密的辩护。实际上，T2开始被视作已经在T1中清楚呈现的东西的一种细化。
出于这种考虑，我们可以获得一些对罗素从事事业的范围的评价。在罗素之前，有两项重要成就与他的计划直接相关。第一，关于自然数的算术理论获得了形式化表述。通过三个初始的算术概念零、后继和自然数，一组公理得到了形式化表述；一组进一步的定义被采纳了，这些定义依据上述初始概念，规定了在数学上相加或相乘的运算；而经典算术之前所有已建立的结论，都已被表明可以从这些公理和定义得出。第二，在罗素之前已经证实，高等数学中的理论，可以在上述已经解释过的意义上被还原为算术。为了我们的目的，我们可以认为数学的所有传统结论都可以被这样还原。
这意味着，算术可以被视作所有数学知识的基础。面对高等数学的某个分支，以及它自己的公理和初始概念，人们总是可以依据算术概念来对这些概念的定义加以形式化表述，并依据算术公理加上为了还原所采取的规定性定义，来证明这些高等分支中的公理。通常来说，这些证明和定义最终都是冗长和复杂的。因此，从事高等数学的人，当然不想通过将所有东西重写为算术词项来进行自己的研究；这种转换通常会如此笨重和难以操作，以至于走这条路会妨碍——如果不是中止的话——数学进步。不过，这些还原在如下意义上在理论上被认为是很重要的：它们表明，数学在认识论上的全部分量，可以被认为是依赖于算术的。如果任何人想依据某种更基本的东西来辩护高等数学的结论，那么算术总是会参与这项工作。由此，如果一个人可以表明，算术应当被接受，那么其他东西的被接受性就随之而来了。
但算术又如何呢？人们是否可以从更基本的东西定义其初始概念并证明其公理？这是罗素和他之前的德国哲学家戈特洛布·弗雷格关心的首要问题。他们的任务是表明算术可以被还原为纯粹的逻辑，因此，一般而言，数学不过是逻辑的细化。这种任务的一部分动机，直接就是数学上的。确定这种已经被用于其他情况的还原是否可用在这里，这是一个重要的数学问题。然而，这项工程同样引起了哲学上的兴趣。
哲学逻辑主义者试图表明，算术，因而一般而言的数学可以还原为逻辑，这主要有三重动机。在讨论这些的时候，我会讨论这些动机的纯粹的或通行的版本，而不会进入这些动机的不同变体所引起的疑难杂症，以及不同逻辑学家所青睐的不同重点。即使罗素自己也在不同时期对逻辑主义还原的哲学重要性持不同的看法，而且他绝没有一直赞同我将要概述的那种经典的、通常的动机。将上述问题一并考虑，我们可以说，这些动机刻画了一个混合的、设想出来的哲学家——经典逻辑主义者——而非任何个人的观点。
逻辑主义还原的第一重和最明显的动机，涉及辩护的认识论目的。在经验论理论的情况下，我们把假设形式化，并用实验数据来测试它们。在这些假设所做的预言被观察性的测试确证出来的范围内，它们得到了证实。在相反的情况下，它们则被证伪。相比之下，在数学中并没有试验或观测。定理通常在这样的基础上被接受：它们得自公理。但这些公理自身如何被辩护呢？一种吸引人的想法是，通过表明数学可以还原为逻辑，人们可以辩护：数学公理不过就是纯粹逻辑原则的逻辑后承。既然大概每个人都接受逻辑，那么辩护的问题也就会得以解决。(2)
这与经典逻辑主义者的第二重哲学动机密切相关。数学真理似乎是先天可知的，独立于经验。这种知识是如何可能的？一方面，认为我们的所有知识都以某种方式得自感觉经验，这是很自然的。另一方面，很难看出，感觉感知如何可以为我们关于必然数学真理的先天知识提供基础和辩护；毕竟，我们无需外出并进行观测，以确证那些算术方程式。不同哲学家对此问题有不同的反应。一些人假定天赋观念是这种知识的来源；一些人主张，存在一个关于真正数学对象的抽象而真实的域，它通过理智直观的一种特殊的类-感知能力被揭示给我们；还有人主张，数学的必然性和先天特征，以某种方式得自我们的心灵加在经验之上的运作和范畴。逻辑主义者对这些答案都不满意。
逻辑主义思潮在历史上一个重要的分支，看到了一种不同答案的可能性。根据这种看法，数学可以被还原为逻辑，而逻辑自身则有着语言上的基础。逻辑原则被认为仅仅由于它们包含的逻辑语词——比如所有、一些、并且、或者和非——的意义而为真。因此，关于我们如何可以拥有关于数学的先天知识的解释，被看作类似于关于我们如何可以拥有单身汉是未婚的这种先天知识的解释。我们如何知道这条关于单身汉的微不足道的真理？我们仅仅决定，以一种独特的方式和意义，来使用语词单身汉和未婚的。像单身汉是未婚的这种句子的真，应当以某种方式得自这些决定。问题是，我们可以仅仅通过知道我们如何决定使用特定的语词，来知道特定的句子以及它们表达的命题为真。因此，根据逻辑主义的一种重要版本，将数学还原为逻辑被用来表明：数学真理是分析的，并因此是可知的，其方式与微不足道的真理——比如我们关于单身汉（据说是）被知道的例子——相同。(3)
我们发现，逻辑主义者在将数学还原为逻辑中的第三重重要的哲学动机，是本体论上的。如果我们考虑一下数学中各个部分的本体论，那么我们似乎不得不设定各种不同东西的存在——自然数、负数、有理数、无理数等。但为了接受数学的结论，我们真的需要设定这么多不同的数学对象的存在吗？将高等数学还原为算术，被认为预示了我们不用这样做。不同类型的数字可以被还原为自然数的不同构造。将算术还原为逻辑则表明，自然数自身可以被还原为特定类型的集合。因此，我们拥有了一种可以被看作使哲学共相剧减的东西。这项始于罗素使用摹状词理论以消除思想的非存在对象（比如食肉奶牛和圆的方）的进程，现在被扩展到自然数和其他数学对象那里。
算术系统
我们现在已经准备好去看看，罗素将算术还原为逻辑中的一些细节。我们从对他算术理论的详述开始。有三个初始词项在该理论中被使用：“N”，被我们用来代表自然数的集合；“0”代表自然数序列中的第一个数字；还有撇号——’——代表后继函数——也即这样一种函数，当被用于任何自然数时，它提供给我们序列中的下一个数字。这三个词项出现在算术公理中，并被认为是无需定义就已经被理解了的。实际上，在给出算术理论时，我们假定自己已经知道了什么是自然数，已经知道了什么是零，并且已经知道了什么叫从一个数字到下一个数字。
在这些算术初始项之外，公理还包含为所有理论共同所有的逻辑词汇——量词、变量和真值函项连接词。还有两个更进一步的符号需要注意——“=”和“∈”。前者是同一性谓词，存在于一个对象及其自身之间。后者代表集合成员关系——一种存在于一个集合中的成员和它们所属于的集合之间的关系。罗素把它们当作逻辑初始项，因此，它们对算术来说并不是独特的。
我们现在已经准备好去陈述算术公理。对每一条公理，我将首先给出形式陈述，然后用英语详述公理所说的内容。
A1．0∈N
零是一个自然数。
A2．∀x（x∈N→x’∈N）
任何自然数的后继都是一个自然数。
A3．～∃x（0=x’）
0不是任何东西的后继。
A4．∀x ∀y ［（x∈N&y∈N&x’=y’）→ x=y］
没有两个（不同的）自然数拥有相同的后继。
除了这四条公理外，我们还有一条公理模式A5，代表可以通过如下方式从方案A5中得到的公理的无限集合：将F替换为任何包含变量x且只包含变量x的自由出现的算术语言中的式子。
A5．［F（0）&∀x（x∈N →（Fx→Fx’））］→ ∀x（x∈N→Fx）在此，F（0）是这样做的结果：将所有代替“F”的式子中的“x”的自由出现，替换为“0”的出现。通俗地讲，F（0）说零“是F”。因此，每一个A5的示例都说，如果零“是F”，且如果无论何时当一个自然数“是F”则它的后继也“是F”，那么所有自然数都“是F”。A5的示例通常被称作归纳公理（induction axioms）。
接下来我们有一对定义，以依据算术初始项来规定相加和相乘的概念。首先是“+”的定义。
D1．∀x ∀y ［（x∈N）&y∈N］ →（（x+0）=x&（x+y’）= （x+y）’）］
对任何自然数x和y而言，将0与x相加的结果是x，而将y的后继与x相加的结果是将y与x相加的结果的后继。
在使用这条定义时，我首先注意到的是，什么叫做把0与x相加。接下来，我们使用相应的结果，加上该定义后件的第二合取支，来算出什么是将0的后继1与x相加；这条定义告诉我们，x与1的和是x+0的后继，也是x的后继，被称作x’。接下来我们再次将此定义用于确定x与2的和是x’’。这个过程可以被重复，以确定对任何一个数字y来说，将y与x相加的结果是什么。既然x可以是任何数字，那么D1就完全确定了任何一对数字的和，即使它并不具备一个清晰的定义所具备的那种为人熟知的形式。
下述例子说明了这点。
说明：3+2=5
（i）（0’’’+0’’）=（0’’’+0’）’ 从D1加上A1和A2得出，它们担保了0’’’和0’’是自然数
（ii）（0’’’+0’）=（0’’’+ 0）’ 从D1、A1和A2得出
（iii）（0’’’+0’’）=（0’’’+ 0）’’ 从在（ii）的基础上在（i）中进行等式替换得出
（iv）（0’’’+0）=0’’’ D1
（v）（0’’’+0’’）=0’’’’’ 从在（iv）的基础上在（iii）中进行替换得出
最后，我们依据相加来定义相乘，（我们用“*”作为相乘的符号。）
D2．∀x ∀y ［（x∈N&y∈N）→（（x*0）=0&（x*y’）= （x*y）+x）］
对任何自然数x和y来说，将x与0相乘的结果是0，而将x与y的后继相乘的结果，是x和y相乘的结果与x的和。
D2以与D1相同的方式起作用。因此，相乘可以依据反复的相加而得以定义，相加又可以依据后继函数的反复运用而得以定义。如同你可以想象的那样，关于相乘的基本事实的证明会非常冗长。但是，通常的结论都可以在包含A1—A5加上D1和D2的算术系统内得到证明。数学的高等分支就可以被还原为这种理论，而且罗素又可以将这种理论还原为他的逻辑系统。
罗素的逻辑系统
接下来我们转向罗素将算术系统还原为的那种系统。我不会详述一般的逻辑原则，它们允许人们直截了当地证明像Pv～P、∀x（Fx→Fa）、∀x∀y（x=y→（Fx↔Fy））等等这样的逻辑真理。我们只把如下事情当作理所当然的：罗素的系统包含的逻辑设备，对这项任务而言已经足够了。但是，我们还会留心罗素逻辑的独特特征，这些特征出现在他这种还原的显著之处。特征之一是一个新的初始符号“∈”，代表集合成员关系（即代表这种关系：当y是一个集合，并且我们说x是y的一个成员时，我们将此关系归属给x和y）。另一个独特特征包括：支配该初始项使用的诸公理，加上一条担保了足够数量的逻辑对象存在的公理。
第一组支配关于集合成员关系符号使用的新公理，由L1的所有示例组成，L1被称作内涵公理模式。(4)
L1．∃y ∀x（Fx↔x∈y）
在此，变量“y”取值范围是集合，并且Fx可以被任何包含变量“x”自由出现（且没有任何其他变量的自由出现）的式子代替。选择不同的式子来承担Fx的角色，会导致该方案的不同示例。每个这种示例都断言，一个包含所有且只包含那些满足该式子（具有被该式子表达的性质）的东西的集合存在。
此公理模式背后的想法是，对于语言中任何包含一个自由变量的开放性的式子而言——从直觉上说，对语言中表达了诸对象的一种性质的每个式子而言——都存在这样一个恰恰由符合此式子（具有被表达的那种性质）的那些事物组成的集合。认为这是一条逻辑规则，实际上就是认为：谈论一个个体x的如此这般的存在，与谈论x在一个如此这般的事物的集合中，是可以互换的。
被L1的示例断言为存在的集合的例子如下：
（i）在代替Fx的式子是任何一个具有是一个< 29的自然数这种意义的式子的地方，比29小的自然数组成的集合的存在被断言了。
（ii）在式子x∈N&x=x代替Fx的地方，所有自然数组成的集合的存在被断言了。
（iii）在式子x≠x代替Fx的地方，空集——即不包含任何成员的集合——的存在被断言了。
（iv）在式子∀z（z∈x↔z≠z）代替Fx的地方，其唯一的成员是空集的集合的存在被断言了。（在此“x”取值范围是集合。）
根据内涵公理模式，对每个式子Φ（x）而言，都存在一个包含所有且只包含那些满足Φ（x）东西的集合。
下一条支配罗素关于集合成员关系的初始项“∈”的公理是L2，它被称作外延公理（the axiom of extensionality）。
L2．∀a ∀b［∀x（x∈a↔x∈b）→a=b］
如果a和b是拥有相同成员的集合，那么a=b——也就是说，没有两个集合拥有相同的成员。（“a”和“b”是取值范围为集合的变量。）
最后的公理L3是罗素的逻辑系统所特有的，被称作无穷公理（the axiom of infinity）。此公理的目的是，确保将算术还原为逻辑所需要的无穷多的逻辑对象的存在。需要这条公理的理由，以及为何它以一种古怪的方式被陈述的理由，只有在我们找到了通向这种还原自身的合适途径之后，才会变得清楚。
L3．∅∉N
空集不是自然数集合的一个成员。
在转向这种还原前，既然我已经描述了罗素的逻辑系统，那么我需要谈一谈它。我已描述的系统，接近于罗素在给出该还原时实际使用的系统。但是，这两者在某些方面有所不同。最重要的区别涉及内涵公理模式。我以一种完全一般化和不受限制的方式，陈述了这种方案。罗素的发现之一是，当该公理模式以这种方式被陈述时，会导致一种现在被称为罗素悖论的矛盾，我们会在适当的时候讨论它。该悖论表明，L1不能以现在所陈述的样子被接受。但幸运的是，到头来有一些限制它的方法，以避开上述矛盾，而与此同时依然差不多允许我们将数学还原为逻辑。我们的策略将是，用我现在陈述的系统来概述这种还原。一旦主要的想法变得清晰，我就会呈现罗素悖论，并简要解释他如何用自己的类型理论来处理它，同时又基本完整地保留这种还原。一旦完成了所有这些，我们就会讨论罗素还原的哲学重要性。
最后一项准备工作：我们会将特定的、已经被定义的词项引入罗素的逻辑系统。它们会作为我们将在还原中使用的各种概念的方便的缩写。
方便的缩写
（下文中，“x”“y”和“s”取值范围为集合）
（i）限定摹状词
Ψ这个z：Φz∃z ∀w ［（Φw↔w=z）&Ψz］
（ii）空集
∅：这个x：（∀z（z∉ x））
（iii）只包含一个成员w的集合
{w}：这个x：［∀z（z∊x↔z=w）］
（iv）包含所有且只包含“是F”（拥有被F表达的性质）的事物的集合
↑z Fz：这个y：［∀z（Fz↔z∊y）］
（v）x和y的交集——即同为二者成员的事物的集合
x∩y：这个s：［∀w（w∊s ↔（w∊x & w∊y）］
（vi）x和y的并集——即或者是x或者是y的成员的事物的集合（x和y放在一起的总含量）
x ∪y：这个s：［∀w（w∊s ↔（w∊x v w∊y）］
（vii）x的补集——所有不在x中事物的集合
Comp（x）：这个y：［∀z（z∊y↔z∉x）］
将算术还原为逻辑
为了将我们的算术系统还原为罗素的逻辑系统，必须首先使用罗素逻辑系统的词项来定义算术初始项，然后从这些定义加上罗素的逻辑公理，导出算术系统的所有公理。通过这种方法，所有的算术定理都成为了逻辑系统的定理。如人们可能想象的那样，其中的窍门在于提出正确的定义。
算术初始项的定义
我们从三个算术初始项的定义开始——零、后继和自然数。前两者的定义如下。(5)
零的定义
0={∅}
0是只有一个空集作为其成员的集合。
后继的定义
一个集合x的后继是，所有包含这样一个成员z的集合y的集合：当z从y中被消除时，留下的东西仍然是x的一个成员。
x’=↑y ［∃z（z∊y & ［（y∩Comp（{z}））∊x］）］
集合x的后继=所有包含这样一个成员z的集合y的集合：y与只包含一个成员z的集合的补集的交集——即与包含除z之外所有东西的集合的交集——是x的一个成员
这些定义以如下方式相互影响：
0’=↑y ［∃z（z∊y & ［（y∩Comp（{z}））∊{∅}］）］
零的后继［即数字1］是所有包含这样一个成员z的集合y的集合：当z从y中被消除时，剩下的是空集——空集没有任何成员。换言之，零的后继是所有包含一个成员的集合的集合，零的后继的后继（即数字2）是所有包含两个成员的集合的集合，以此类推。
关于这个过程有三点需要注意。第一，这不是一种循环。结果数字2是所有有两个成员的集合的集合。但是，我们并没有使用有两个成员的集合（或包含两个成员的集合）的概念来定义数字2。相反，我们可以将数字2定义为1的后继，而1又可以被定义为零的后继。在此，最基本的概念——即零和后继——其自身是在没有任何算术概念的情况下得以定义的。因此，这里没有循环。
第二，你应当可以从我们的这种过程中看出，从直觉上讲，没有两个自然数m和n——通过这种后继的链条所得——可以拥有相同的成员。如果n由所有且只由有n个成员的集合组成，而m由所有且只由有m个成员的集合组成，假定m和n是不同数字的话，那么没有一个集合可以既是m的成员又是n的成员。另一种表达这一点的方式是，如果根据罗素主义的定义n和m是自然数，并且如果它们拥有相同的成员，那么n和m必定是同样的数字。尽管我们在此没有给出关于这一点的证明，但它在形式上可以从罗素的逻辑系统公理中得到证明。我们将在随后的还原中回到这一点，因为它在其中一条算术公理的证明中起了作用。
关于定义个体数字的过程，你应当重视的第三样东西是：它是何其的自然。罗素在《数理哲学导论》第二章开头处谈到了这一点。
在找寻数字的定义时，第一件需要弄清楚的事情，是我们可以称之为询问的语法的东西。很多哲学家在尝试定义数字时，实际是在着手于定义杂多（plurality），而这是一种与数字非常不同的东西。数字是诸多数字的特征，正如人是诸多人的特征。而一种杂多则不是数字的一个示例，而是某个独特的数字的示例。例如，一个三人组是数字3的示例，而数字3是数字的示例；但三人组并不是数字的示例。这一点似乎是很初步的而且几乎不值得注意；但事实证明，除了少数例外，这一点对哲学家来说过于微妙了。
一个特殊的数字不与任何包含那个数字的项的合集等同：数字3不同于由布朗、琼斯和罗宾逊组成的三人组。数字3是某种为所有三人组所共有的东西，也是将它们与其他合集区别开来的东西。一个数字是某种刻画了特定合集——即那些包含那么多数目的合集——特征的东西。(6)
我们可以通过指出如下东西来阐明罗素的观点：“是红的”这种性质与任何红色的事物都不同。相反，它是某种为所有红色的事物所共有的东西。同样，数字3与任何三个事物的集合都不同；相反，它是某种为所有三个事物的集合所共有的东西。我们可以说，数字3是这样一种属性：是包含三个成员的集合。然而，在罗素的系统中，关于性质的谈论，被关于集合的谈论所取代。因此，对他而言，数字3变成了这样一个集合：它包含所有具有三个成员的集合。所有三人组的共同之处是什么？成员数量是数字3。
我们现在已准备好定义最后一个算术初始项——N——我们用其代表自然数的集合。既然已经有了零和后继，我们似乎就可以将自然数的类定义为这样一类集合：它们可以通过从零开始并有限多次地运用后继的方法而得到。但是，这预设了有限数目（finite number）的概念作为我们的逻辑初始项，而它实际上并不是。相反，它是一个需要定义的数学概念。事实上，在被用于上述定义时，它正是我们试图定义的概念，因为，对某个自然数n来说，将后继使用有限多次，正是将其使用n次。所以我们得再想想。
假设我们进行这种尝试：
N=那个包含零的、在进行后继运算后是闭合的集合——也就是说，包含其每个成员的后继的集合。
初看上去，我们想称之为自然数的所有东西都会被归入这个定义。但这只是幻觉。该定义是不可接受的，因为不存在符合上述条件的那种集合。例如，下述每个集合都符合条件：该集合包含零，且在进行后继运算后是闭合的。
Set 1{0，0’，0’’，0’’’，……}
Set 2{0，0’，0’’，0’’’，……{{比尔}}，所有包含比尔加上其他某物的集合，……}
Set 3 {0，0’，0’’，0’’’，……{{比尔}，{玛丽，罗恩}}，{{比尔}}的后继和所有包含玛丽与罗恩的三元组的集合的并集，……}
有了这个结果，我们就需要某种方法来丰富被用于定义“N”的条件，以排除除了set 1之外的集合。我们可以这样来做：
自然数的定义
自然数的集合=包含零的并且在进行后继运算后是闭合的最小集合
N=↑x ［∀y（（0∊y &∀z（z∊y→z’∊y））→ x∊y）］
（“x”和“y”取值范围为集合）
自然数的集合，是包含所有且只包含这些集合x的集合，x是任何这样的集合y的成员：它包含零并且在进行后继运算后是闭合的。
这样，依据罗素逻辑系统中的概念，就得出了关于算术概念定义的结论。在将算术还原为逻辑中，所有仍需完成的是，表明算术公理可以在这些定义的帮助下从罗素的逻辑公理得到证明。
算术公理的证明
首先的两条公理显而易见地得自我们已经采纳的定义。
A1．0∊N
0是一个自然数。
使用“N”的定义，我们看到，这意味着零是包含零且在进行后继运算后是闭合的最小集合的成员。因此，它是一条微不足道的真理。
A2．∀x（x ∊N→x’∊ N）
任何自然数的后继仍然是自然数。
再次使用“N”的定义，我们看到，这意味着，如果x是包含零且在进行后继运算后是闭合的最小集合的成员，那么x的后继也是这样一个集合的成员。这仍然是微不足道的——它得自一个集合在进行后继运算后是闭合的意味着什么。
接下来请考虑A3，它说零不是任何东西的后继。
A3．～∃x（0=x’）
这可以通过归谬法得到证明：
（i）假设对某个x来说，零是x的后继。
（ii）通过零的定义可知，这意味着{∅}=x’。
（iii）通过后继的定义我们得到：对{∅}的任何一个成员y来说，都存在一个y的成员z，如果将z从y中排除，那么会剩下x的一个成员。
（iv）由此得出，存在一个∅的成员z。
（v）但这是不可能的，因为∅没有任何成员。
（vi）因此，（i）为假；零不是任何东西的后继。这证明了A3。
我们现在跳转到公理模式A5。
A5．［F（0）&∀x（x∈N →（Fx→Fx’））］→∀x（x∈N→Fx）
在此F（0）是这样做的结果：将所有代替“F”的式子中的“x”的自由出现，替换为“0”的出现。通俗地讲，F （0）说零“是F”。因此，每一个A5的示例都说，如果零“是F”，且如果无论何时当一个自然数“是F”则它的后继也“是F”，那么所有自然数都“是F”。
我们将证明此方案的一个任意的示例。为了证明此示例，我们将假定其前件，并尝试证明其后件。前件说：（i）零是F；（ii）无论何时，只要当一个自然数是F，那么它的后继就也是F。我们必须表明，如果这为真，那么其后件也必定为真——也就是说，（iii）所有自然数都是F，这必定为真。我们从考虑这样一个类开始：它由所有且只由那些是F的自然数组成。内涵公理模式L1保证了存在这样一个集合。前件的两个条款（i）和（ii）告诉我们，该集合包含零，并且在进行后继运算后是闭合的。回忆一下我们对自然数的定义——那些是每个这样集合的成员：这种集合包含零并且在进行后继运算后是闭合的。既然我们已经看到，那些是F的自然数的类是其中一个集合，那么我们就知道，每个自然数都必定是它的一个成员。因此（iii）为真——每个自然数都是F。通过这种方法，我们可以证明公理模式A5的任何示例。
为了完成上述那种还原，所有还需要证明的就是A4。
A4．∀x ∀y ［（x∊N & y∊N & x’=y’）→ x=y］
没有两个（不同的）自然数有同样的后继。
为了证明这一点，我们假定
（i）x和y是自然数；
（ii）x’=y’
然后表明（iii）得自它们。
（iii）x=y
为了表明（iii）得自它们，我们会考虑两种可能性，它们最初似乎有些奇怪，但随着证明的推进就会变得清晰起来。
可能性1
x’=y’≠∅（即x’、y’是包含成员的集合）
可能性2
x’=y’=∅
首先请考虑可能性1。（a）对x’的（即y’的）任何成员w来说，消除它的一个成员z会提供给我们x的一个成员s（得自后继的定义）。（b）同样，对y’的（即x’的）任何成员w来说，消除它的一个成员z*会提供给我们y的一个成员s*（得自后继的定义）。（c）既然x’（y’）是一个数字，那么s就是x和y的一个成员，s*也是如此。（得自如下事实：当n’是一个数字时，无论n’的成员w的哪个成员被消除；得到的结果总是n的一个成员。因此，无论x’（即y’）的成员的哪个成员（z或z*）被消除，最后得到的集合一定既是x的成员又是y的成员）(7)。（d）(8)因此，x和y是拥有同样成员的数字。从我们对数字的构造中可以看出，这担保了x=y。(9)假设我们可以排除可能性2，以上足以证明A4。
现在是时候转向那种可能性了。∅如何可能是任何东西的后继？好吧，设想只有10个存在的对象可以被用于对数字的构造。根据罗素的定义，10=所有有10个成员的集合的集合。现在请考虑10的后继。根据定义，它是所有那种集合y的集合：y包含一个成员z，当z从y中被消除时，会留下一个有10个成员的集合。换言之，10’=所有有11个成员的集合。但如果在宇宙中只有10个事物被用于构造数字，那么就不会存在有11个成员的集合。在那种情况下，所有有11个成员的集合的集合就会是空集∅。万一这样，10的后继10’就会是空集∅。
接下来请考虑10’的后继——即10’’。根据定义，它是所有那种集合y的集合：y包含一个成员z，当z从y中被消除时，留下的东西会是∅的一个成员。既然∅没有成员，也就没有这样的y：将它的一个成员消除后，留下的东西会是∅的一个成员。因此，在我们所考虑的这个离奇的场景中，10’’=∅。这意味着我们得出10’=∅=11’（即10’’）。但10≠11，因为11=∅，而10=所有有10个成员的集合的集合，而根据假定这并不是空集。但这会符合A4——因为我们会得出x’=y’，而不是x=y。因此，如果宇宙中只有十个对象——或它确实只有有限多个对象——被用于构造罗素主义的数字，那么A4就会为假。
正是避免这种结果的需求，促使罗素设定了无穷公理，一条初看上去有些奇怪的式子
L3．∅∉N
作为他逻辑系统的一项公设。请注意，在罗素系统的语境中，这条公理有如下作用：担保无限多对象的存在，而无需使用有限多或无限多这样的概念作为初始项。有了L3在恰当的地方起作用，可能性2就被刻画为是不可能的，而A4就可以从逻辑系统中得到证明。还原便这样完成了。
罗素悖论和类型理论
看过罗素如何将算术还原为逻辑后，我们现在已经准备好仔细查看他逻辑系统中两条特殊的公理——不受限制的内涵公理模式（the unrestricted axiom schema of comprehension）
∃y ∀x（Fx↔x∊y）
和无穷公理
∅∉N
在无穷公理的情况下，人们可能怀疑，关于有多少对象存在的问题，实际上仅仅是一件关于逻辑的事情，而因此人们可能怀疑，无穷公理应当被当作一条真正的逻辑公理。罗素考虑过这些，并至少在最初相信这种忧虑可以被摒除。例如，如果集合被当作对象，那么人们似乎可以将它们不受限定地制造出来——∅，{∅}，{{∅}}，等等。这似乎并不困扰人们去设想存在无限多的事物，如果这样的纯粹集合被算作事物的话。或者，为了该论证，让我们设想只存在有限多的具体的殊体。假定n是这种殊体的数量。那么就存在2n个这种殊体的集合，2到2n个这种集合的集合，等等。继续这个不受限定的过程，并将所有这些放在一个单独的集合里，我们显然会得到一个无限的集合。再说一次，如果该集合的所有成员都被算作对象，那么无穷公理似乎就不再是问题了。
尽管罗素最初相信这些论证，但除了其他方面外，他很快发现一个严重的问题，这阻止人们说服自己去相信：无穷公理不足为虑。(10)这个问题就是罗素悖论，而他解决此问题的方法就是类型理论。该悖论产生自不受限制的内涵公理模式。
∃y ∀x（Fx↔x∊y）
此公理模式的示例，产生自将Fx替换为逻辑语言中任何只包含自由变量“x”的式子。问题是，无论代替Fx的式子究竟是什么，都必定存在这样一个集合：它包含所有且只包含那些符合该式子的事物——“是F”的事物的集合。在有些情况下，这可能是一个空集。但这也没问题；空集也是一个集合。
但是，假设我们将Fx替换为式子
～x∊x
这样做我们会得到作为罗素逻辑系统公理的（1）。
1．∃y ∀x（～x∊x↔x∊y）
存在一个包含所有且只包含那些不是其自身成员的事物的集合。让我们引入一个新的符号“y”作为这种假定集合的名称。有了“y”的这种定义，如果（1）为真，则（2）一定为真。
2．∀x（～x∊x↔x∊y）
所有事物都是这样：它是y的一个成员，当且仅当它不是自身的一个成员。
但现在，既然所有事物包含每个单独的事物，那么（2）做出的主张必须包含y自身。因此，如果（2）为真则（3）必定为真。
3．（～y∊y↔y∊y）
y是其自身的一个成员，当且仅当它不是自身的一个成员。
但（3）是一条矛盾式，并因此不可能为真。既然（3）是（1）的一项逻辑后承，而（1）又是内涵公理模式的一个示例，这意味着，罗素的逻辑系统是自相矛盾的。这就是罗素悖论。
该悖论的存在，要求罗素修正自己的系统，以使得它不会再产生出这条矛盾。这样的修正，从关于此问题是如何产生的的诊断发展而来。该问题产生自内涵公理模式的两个方面：（i）将方案中的Fx替换为逻辑语言中任何式子的能力，以及（ii）将全称量词∀x解释成可以取值为任何事物。既然公理模式的这两个方面结合在一起产生了矛盾的结果，那么要避免这种结果，就要求改变二者中的一个或两个。罗素的类型理论就是一种同时改变两个方面的方法。
现在我将给出此理论一种非常概要和简单的概述。我们从一种关于宇宙的等级观开始。在原初最基本的层次上，我们有个体——即各种具体的殊体——包括人、物理对象等等。在下一个层次上，我们有所有可以通过使用之前层次上的个体作为其成员而形成的集合。在接下来的层次上，这个过程被重复，我们以此得到那些以个体的集合作为其成员的集合。这套等级会继续下去，每个层次都被一个囊括了之前层次上事物的所有集合的层次所跟随。（你可能注意到，根据这种做法，我们从未得到这样的集合：其成员来自不同的层次——这是一条可以被超越的限制。但是，既然我们在对数字的构造中从不需要这样的集合，我们将继续遵循这种简单的方案。）
与这种等级宇宙相应的，是一种有等级的逻辑语言。这种语言，是我们原初的逻辑语言加上如下两条修订。（i）变量和名称在被写上下标时，表示它们所命名的事物的层次，或它们的取值范围是哪个层次上的事物。比如，我们有xi，xii，xiii，……，在名称的情况下也是如此。（ii）这些下标被用于限制哪些式子是有意义的而哪些没有。我们对这种限制的旨趣，可以通过式子xn∊yni和xn=yn加以阐明。(11)在包含二元谓词∊的原子式的情况下，该限制要求，出现在谓词右侧的单称词项，被指示为在直接出现在如下层次之上的那个层次上，即出现在谓词左侧的单称词项被指示为所在的那个层次。而在包含同一性谓词“=”的原子式的情况下，在谓词两侧的单称词项要求被指示为在同一层次上。违反了这些限制的式子——例如xn∊yn和xni=yn，都被声称是无意义的。
增加这些限制的原因是，它们允许我们以一种阻止上述矛盾的方式，重述内涵公理模式。
∃yni∀xn（Fxn↔xn∊ yni）
其示例得自：将Fxn替换为任何在n层次上的式子，而式子中唯一自由出现的变量是xn。（一个在n层次上的式子，是一个包含n层次下标，而不包含其他更高层次下标词项的式子。）
从直觉上说，这条公理模式告诉我们，对所陈述的任何情况——该情况是关于任意层次n上的事物——而言，在随后一个层次上都存在这样一个集合：它包含所有且只包含那些在层次n上符合此条件的事物。请注意，式子～x∊x和～xn∊xn不能被用来替换Fxn，而应被当作是无意义的。式子～xn∊yni也不能用来替换Fxn。尽管这个式子是有意义的，但它却不是一个在层次n上的式子，而且除此之外，它包含的自由变量不止xn。因此，它不能被替换进此方案中以得到一个示例。为了得到那样一个示例，人们必须使用一个陈述关于一个层次或类型上，且无关更高层次上事物的情况的式子。另外，无论我们用层次n上的哪个式子代替Fxn，都不会获得如下这样的示例：在其中，任何在接下来一个层次上的集合，会进入到量词的值域范围内。
如果我们拥有了此方案的一个真正的示例，那么它就断言了，在n之上那个层次上有一个这样集合存在：它包括所有且只包括那些在层次n上满足某特定条件的事物。让我们将这个集合称为yni。有了任何一个这样的示例，我们都知道了具有如下形式的事情
∀xn（Fxn↔xn∊yni）
为真。当我们去除全称量词，并将变量xn的出现替换为层次n上任意对象的名称，进而得出结论时，我们就被禁止在接下来的层次上使用任何对象的名称；因而我们不能选择yni。所以，最初得自不受限制的内涵公理模式的那种矛盾，无法在新的逻辑类型系统中被推导出来。这是新系统的一个重要长处。
该系统的另外一项值得一提之处是，它具有一定程度上的自然性。有人可能认为，当我们想到一个集合时，我们首先想到它的成员，然后把这个集合当作一种这些成员在一起的聚集物。在某种意义上，这些成员好像在概念上先于集合。如果我们真的是这样思考集合的话，那么说一个集合可以是其自身的一个成员就是荒诞的。而如果这是荒诞的，那么人们会把它当作是无意义的，这也就无可厚非了。
当然，以上是对罗素类型理论一种非常简单和概要的导论，而这种理论自身是一个极为复杂的主题。幸运的是，我们可以忽略大部分的复杂之处。为了我们的目的，有三个基本点需要强调。第一点涉及语言和实在间被假定的平行关系。就像一个集合不可能是其自身的一个成员一样，罗素认为，说一个集合是其自身的成员不仅是错误的，而且是无意义的。正如等级中一个层次上的某个成分不可能与另一个层次上的成分相等同一样，说一个层次上的某物与另一个层次上的某物等同或不等同，在罗素看来也是无意义的。你既可以把这一点看作是世界结构对语言中什么是有意义的所加的限制，也可以看作语言中可能的意义的范围对我们关于世界的观念的限制。或许，将世界或语言中的任何一方置于在先的地位，都是误导人的。根据罗素的看法，最准确的说法可能仅仅是，存在那种平行关系，而试图说出任何更多的关于什么应当对此负责的内容，都是竹篮打水一场空。如我们随后将看到的那样，关于语言和世界间存在一种重要的平行关系的想法，在罗素和维特根斯坦随后的著作中、在他们的逻辑原子主义系统中，得到了进一步的发展和清晰的表达。
关于类型理论需要注意的第二点是，它是何其地具有限制性。在对其所做的非正式的呈现中，我曾数次说过或试图说这样的事：没有一个层次上的成分与任何其他层次上的成分相等同，以及没有集合是其自身的一个成员，还有一个集合不可能是其自身的一个成员。但如果类型理论是正确的，那么所有这些陈述都是无意义的。说没有集合与它的任何成员相等同，这似乎为真。但是，如果罗素的类型理论为真，那么我们不可能有意义地说出这点。一般而言，当解释类型理论时，人们发现，实际上自己会不可抗拒地去说如下这样的事：一旦人们拥有了类型理论，这些事就都被声称是无意义的。
对这种纷扰的一种回应可能是，主张类型理论中采用的下标系统以某种方式表达或显示了，当人们说出语词没有集合与其任何成员相等的同时所白费力气地试图说出或断言的东西。这种下标系统显示出这些，仅仅因为形成“=”的规则要求等同的下标，而形成“∊”的规则却禁止那样的下标。如我们将会看到的那样，关于一个符号系统可能显示某种不能被有意义地说出的东西的想法，实际上是随后将被采用的另一种想法——特别是被维特根斯坦所采用（尽管与类型理论无关）。
关于类型理论需要注意的第三点，也是本章最重要的任务是，它如何影响将算术还原为逻辑。如果将这种理论置于合适的地位，那么这种还原就在此等级中的四个层次上得出。尽管任何四个随后的层次都可以参与这种还原，但最直观的还是最初的那四个层次。
将算术还原为逻辑所涉及的逻辑类型
类型i （具体的）个体
类型ii个体的集合
类型iii个体集合的集合（数字在这个层次上。）
类型iv （个体集合的集合）的集合（自然数的集合出现在这里。）
关于零、后继和自然数的定义现在可以被这样重述：
零的定义
0iii={∅ii}
零是iii-层次上的集合，其唯一成员是ii-层次上没有成员的集合。
后继的定义
一个iii-层次上的集合xiii的后继，是所有ii-层次上包含一个个体zi——当zi从yii中被消除时，留下的东西仍然是xiii中的一个成员——的诸集合yii的集合。
xiii’=↑yii［∃zi（zi∊yii& ［yii∩Comp（{zi}）∊xiii］）］
一个iii-集合xiii的后继=所有ii-集合yii的集合，其中yii包含那样一个个体zi，而yii与ii-层次上只包含一个对象zi的集合的补集——即与ii-层次包含除zi之外每个个体的集合——的交集是xiii的一个成员。
自然数的定义
自然数的集合=iiii-层次上包含零（即iii-层次上其唯一成员是ii-层次上空集的集合）的最小的集合，且此集合在进行后继运算后是闭合的。
Niiii=↑xiii［∀yiiii（（0iii∊yiiii&∀ziii（ziii∊yiiii→ziii’∊yiiii））→xiii∊yiiii）］(12)
自然数的集合是iiii-层次上的集合，它包含所有且只包含那些iii-层次上的集合：这些集合是每个iiii-层次上集合——这种集合包含iii-层次上的集合零，并且在进行后继运算后是闭合的——的成员。
出于这种考虑，让我们重访一下无穷公理在证明算术系统中的A4时所起的作用。A4陈述说，没有两个不同的自然数拥有相同的后继。为了证明这一点，我们需要假定iii-层次上没有成员的集合不是任何自然数的后继。现在被陈述为如下样子的无穷公理担保了这一点：
～（∅iii∊Niiii）
设定这一点，就是假定总是会存在足够多的i-层次上的事物——即具体殊体——以制造ii-层次上任何具有有限大小的集合。因为否则的话就意味着，如果在i层次上只存在10个个体，那么数字10就会成为iii-层次上这样的一个集合：其唯一成员是ii-层次上包含所有10个i-层次上个体的集合。如果将后继的定义用在这里，我们会发现，没有一个ii-层次上的集合包含这样一个个体：当你把它移除时，还剩下一个包含所有10个i-层次上个体的集合。这将意味着，10的后继是iii-层次上的空集。无穷公理排除了这一点。以类似的方式，它排除了如下可能性：我们会耗尽被用于构造数字的i-层次个体。因此，在假定无穷公理的时候，我们就假定了无穷多个具体殊体的存在——即无穷多个不是集合的事物的存在。
如果在等级中上升得更高，并在更高的层次上将算术还原为逻辑，是不是对我们更有帮助呢？并非如此。如果只有有限多个i-层次个体，那么将只会存在有限多个ii-层次的个体的集合，只存在有限多个iii-层次的ii-层次上集合的集合，对等级中每个层次来说都是如此。既然我们在罗素主义的还原中总是会需要一条无穷公理，那么我们就总是需要假定有无穷多个非集合的东西。这条假定合理吗？好吧，或许合理。也许材料和/或空间的区域是无限可分的，因此提供了无穷多的非集合的东西。但是，情况究竟是否如此，还完全不清楚。当然，很难看出无限多这样东西的存在，如何可以成为某种仅仅关于逻辑的事情。
我要说，有各种方法将算术还原为关于如下集合的断言：它们不要求针对具体个体——或一般而言，针对非集合的东西——的无穷公理。但是，这些进行还原的方法时常会摒除掉罗素的类型理论，并用这种办法——完全放弃内涵公理模式、代之以一些非常不同的公理——来处理罗素悖论。当你用其中一种方法来做事情时，仍然可以将算术还原为你自己的集合论系统。但这些集合论系统，似乎更像是将数学理论从它们自己的主题中分离出来，而非从纯粹的逻辑系统中分离出来。
这清楚地表明，罗素将算术还原为逻辑的一种方法是不成功的。人们可以将算术还原为集合论的形式化系统，如罗素所说的那样，这个系统可能在某种意义上是更为基本的。但是，人们似乎不能将算术还原为任何配得上纯粹逻辑这个名称的东西。如果这是正确的，那么最初将数学还原为逻辑的宏大哲学计划，就必须被认为是失败的。
盖棺以定论，决定成败的最后的致命一击，在《数学原理》之后二十年，以库尔特·哥德尔关于算术不完全性证明的形式出现。概言之，哥德尔证明了：任何一致的一阶算数理论（像我们在讨论罗素的还原中所利用的那个理论）必定会留下一些不可证的算术真理。充其量，任何形式化的算术理论——它允许从一个算术公理的定集合证明算术定理——都将会有这样的结果，即任何可证的定理都为真；但是，任何系统都不可能证明所有且只证明这些算术真理。简言之，算术真理自身不能被完全形式化。既然哥德尔的结论暗含说，没有一种公理的集合足以得出所有且只得出这些算术真理，那么毋庸置疑，它表明没有一种逻辑公理的集合——无论纯粹与否——可以做到这点。
逻辑主义的哲学重要性
检验了罗素将算术还原为自己逻辑系统的工作后，让我们转向与这种逻辑主义工程相关联的哲学动机。罗素的技术成就在怎样的程度上没有辜负这些动机？回忆一下，经典逻辑主义者的动机之一是，用逻辑来辩护算术，并由此辩护所有经典数学。一个相关联的动机是，解释关于数学的先天知识是如何可能的。经典逻辑主义者通过如下方法将这些捆绑在一起：将从数学到算术，再从算术到逻辑的双重还原，视作表明了这样一点，即经典数学的所有结论都是分析的。
这种立场的一种清晰的表述，由卡尔·亨佩尔（Carl Hempel）在写于1945年的《论数学真理的本质》（On the Nature of Mathematical Truth）(13)中给出。谈及辩护的问题，亨佩尔写到：
如果因此数学应当是在数学概念所意图的意义上的、关于数学概念的正确理论，那么它的确证就不足以充分地表明，整个系统可以从皮亚诺公理（Peano postulates）［即在罗素的还原中被使用的形式化的算术系统］加上适当的定义得出；相反，我们需要进一步询问，当这些前提在它们的通常意义上被理解时，皮亚诺公理实际上是否为真。当然，只有在词项“0”“自然数”和“后继”的通常意义被清晰地定义之后，这个问题才能得到回答。(14)
在这段话中亨佩尔指出，他认为，辩护或确证数学公理的问题，要求定义出现在它们中的算术初始项。在说了这些之后，他立即转向逻辑主义——实际上就是罗素主义——的定义，他认为，这些定义给出了词项“0”“自然数”和“后继”的“通常意义”，他还强调了如下事实：使用这些定义加上罗素逻辑系统中的公设，人们可以证明这些算术公理为真。(15)在亨佩尔看来，这解决了辩护问题。
在概括经典逻辑主义的立场时，他说道：
数学是逻辑的一个分支。在如下意义上，它可以从逻辑中得出：
a．所有的数学概念，即所有的算术、代数和分析概念，都可以依据四个纯粹的逻辑概念加以定义。
b．所有数学公理都可以通过逻辑原则从那些定义中推导出来（包括无穷公理和选择公理）。
在此意义上可以说，这里所界定的数学系统中的命题，由于所涉及的数学概念的定义而为真；或者，这些命题澄清了我们通过定义而赐予算术概念的特征。因此，数学命题具有同样无可置疑的确定性，这种确定性是“所有单身汉都是未婚的”这样命题的特征，但它们同样完全缺失与那种确定性相关联的经验内容：数学命题缺乏所有的实际内容；它们没有传递任何关于经验性主题的信息。(16)
不仅数学命题应当具有“无可置疑的确定性”这种属性——因为它们是分析的——而且关于它们如何可以被先天知道为真的解释，也应当在本质上与关于我们如何可以知道琐事所有单身汉都是未婚的为真的解释相同。我们可以知道它们为真，因为它们由于意义而为真，而且我们可以知道它们的意义是什么。简言之，根据经典逻辑主义者的看法，传统数学的真理是分析的，因为逻辑主义还原已经表明了它们在本质上是逻辑真理，而逻辑真理自身是分析的或由于意义而为真。
值得注意的是，罗素自己并未完全或明确地接受这幅图景。最初，他似乎确实认为，逻辑主义还原要潜在地回应对算术公理进行辩护的要求。但是，他很早便开始认识到该观点的一个重要问题。在算术公理的情况下，在前理论的意义上讲，我们对算术公理比对任何被称作逻辑系统的公理都更为确定，而算术公理可能被还原为那种逻辑系统的公理。例如，似乎很清楚的是，罗素关于内涵和无穷的公理——如同被他的逻辑类型理论所修订的那样——与逻辑主义者用它们所得出的算术公理系统相比，引起了多得多的问题，而且受到更大程度上的合理怀疑。我们可以通过如下说法来表明这一点：罗素的逻辑公理自身，比算术公理——他将这些算术公理还原为逻辑公理——更需要辩护。既然如此，如果从一开始就真的存在对算术公理的辩护问题，那么它并没有通过将算术公理还原为一个更有问题的公理系统——无论人们是否将逻辑这个词与该系统联系起来——而得以解决。
确实，罗素开始相信，为他的逻辑前提进行辩护的一个实质性部分在于如下事实，即它们可以被用于得出从本质上说更自明的算术公理。(17)在一个特定的范围内，他开始把辩护的方向看作是反转过来的了。他还认为，这种还原在理论上是重要的，这有如下三条理由。第一，这表明，算术公理，以及借助于它们的经典数学的其他定理，可以从一个逻辑系统中得出，这说明我们关于数学知识的体系是如何被组织起来的，以及该体系的不同部分间是如何彼此相关的。第二，这表明，遵循基础性的逻辑和集合论原则的日常算术，可以导致对数学知识有用的扩展和统合，比如将关于自然数的算术扩展为超限算术理论（the theory of transfinite arithmetic）。第三，罗素主张，通过阐明数学的逻辑本质，人们可以清楚地了解这样的哲学问题：数学知识等于什么，以及它如何被获得。(18)
关于最后一点，我并不完全确定他想的是什么。然而，在指出了逻辑主义并没有解决辩护算术的问题后，我们还有这样的任务，即评价逻辑主义在解释我们的数学知识是如何可能问题上的贡献。让我们暂时将数学真理是否被辩护的问题搁置。同样搁置任何关于我们是否知道它们为真的问题。它们当然得到了辩护，而且我们当然知道它们为真。不管怎样，我们知道非常多的算术真理。此外，我们似乎不是通过观察和经验，而是先天地知道它们。亟待解决的问题是，将算术还原为逻辑的逻辑主义还原，是否提供了关于那些我们先天地知道为真的算术陈述的分析，这种分析揭示了上述知识是如何可能的。
这与摩尔对极端怀疑论的回应有一种相似之处。面临怀疑论的挑战，摩尔当然会坚称，我们知道在自己心灵之外存在着事物。这无需进一步的辩护。哲学分析的基本任务是，清楚地说出一种关于知识的观念，以及当人们知道某个外部对象存在时清楚地说出一种关于我们知道什么的观念，该观念会允许我们解释自己如何知道那些最显而易见地知道的东西。我们现在所探寻的、关于数学先天知识内容的问题，类似于摩尔所问的关于外部世界知识内容的问题。
逻辑主义还原是否提供了一种对我们先天知道为真的算术断言内容的分析——这种分析解释了那种知识是如何可能的？在尝试回答这个问题时，为了进行论证，让我们假定一种可能看上去有问题的论点。让我们假定，我们先天地知道罗素逻辑系统的基本原则，而那种知识自身是很容易得到解释的。有了这些，我们知道，如果算术句子真的与逻辑句子——罗素在进行还原时将算术句子翻译为这些逻辑句子——意味相同的事情，那么我们获得这种知识——关于被那些算术句子表达的命题为真的知识——的能力就很容得到解释。
但算术句子与逻辑句子——罗素将算术句子翻译成这些逻辑句子——真的表达同样的命题吗？这看上去似乎是个奇怪的问题。难道罗素不是仅仅依据逻辑概念来定义算术概念吗？没错，他是这样做的。但如此一来，根据这些定义，算术句子难道不是显然必定与逻辑句子表达同样的命题吗？好吧，既是又不是。
是的，如果你喜欢的话，可以简单地规定，你通过各种数学符号想意指的东西，就是由它们在罗素主义逻辑系统中的逻辑译文所表达的东西。如果你做出这种规定，那么对你来说，算术句子就会表达与逻辑句子相同的命题。但是，假设我们来问另一个问题。在罗素想出他的还原之前，算术句子表达了怎样的命题？在罗素之前，数学家、哲学家和普通人都熟悉算术。他们使用算术句子，并进行算术运算。想必他们所使用的算术句子有意义，并表达了很多人知道为真的命题。即使在罗素的发现之后，很多人也从未听说过他或任何其他人将算术还原为逻辑的尝试。尽管如此，这些人还是知道大量的算术。那么，当他们知道“（3乘以3）加上（4乘以4）=（5乘以5）”时，他们知道的是什么？他们所知道的命题，与极其复杂的逻辑句子——罗素会把那个简单的算术句子翻译成这个逻辑句子——所表达的命题一样吗？
有两种指向否定结论的论证。（i）罗素的命题过于复杂和陌生，以至于无法将关于它的知识，归属给所有我们这些通常知道“（3乘以3）加上（4乘以4）=（5乘以5）”的人。很多知道一条算术真理的人，并不理解对它的罗素主义的翻译，即使人们把这解释给他听。这使得如下说法变得令人难以置信：他们已经知道的东西，一向就是那种需要罗素（或弗雷格）那样的天才去发现的东西。（ii）在罗素完成他的还原后，显然有多种不同方法来获得差不多同样的结果。人们不需要把零当作只有一个空集作为成员的集合，也无需将后继完全定义为罗素所定义的样子。有各种在实质上的不同方法，依据逻辑或集合论的概念来定义算术概念。有了两种这样的方法，就有两种实质上不同的方法来翻译像（3乘以3）加上（4乘以4）=（5乘以5）这样的算术句子。当澄清细节后，这两种可替换的逻辑翻译就很可能表达了不同的命题。因此，它们不可能都表达了（3乘以3）加上（4乘以4）=（5乘以5）这个命题。但与其中一方相比，似乎并没有更多理由说，另一方表达了上述命题。相反，最合理的说法可能是，二者都没有表达与算术句子完全一样的命题，尽管二者分别都在某种意义上表达了与那个命题相等价的命题。
但是，如果我们这样说，那么就必定面临一种困难。设想某个前罗素主义的数学家，或某个聪明的四年级生，或某个这样的人：他没有听说过罗素或将算术还原为逻辑，但却知道（3乘以3）加上（4乘以4）=（5乘以5）。如果这个人所知道的那个命题，与罗素还原中相应的逻辑命题并不完全是同一个命题，那么罗素的命题如何可以被说成是对（3乘以3）加上（4乘以4）=（5乘以5）这个命题的分析？进一步说，也是最关键的地方是，一种关于罗素的命题如何是先天可知的解释，如何可以提供任何一种关于普通人的命题——（3乘以3）加上（4乘以4）=（5乘以5）——是如何被先天知道或先天可知的解释？如果它们不是同样的命题，那么对其中一方如何被或可以被知道的解释，似乎就与另一方如何被或可以被知道的解释非常不同。
我们在此面对的问题是反复出现的问题（recurring problem）的一个示例，是一种悖论，当哲学家试图通过提供一种令人惊奇和意义深远的、关于在陈述此问题时涉及的诸多概念的分析，来解决真正实质性的哲学问题时，该问题可能会突然出现。人们从某些关于特定常识命题——比如我知道存在物理对象，我知道我有一只手，或我知道（3乘以3）加上（4乘以4）=（5乘以5）这样的命题——的在哲学上令人困扰的问题出发。人们可能像摩尔和罗素那样感觉到，自己确实真的知道这些事情。但作为一个哲学家，人们想理解这种知识是如何可能的。在物理对象陈述的情形下，人们可能想知道，关于自己感觉——这些感觉构成自己的基本材料——的知识如何可能引起关于物理对象的知识——这种知识远远超出了自己的感觉材料。在数学的情形下，人们可能想知道，自己如何可以拥有关于数学命题的先天知识——这种知识独立于经验。
摩尔和罗素所追求的方法，是将人们所知的常识命题，分析为它们应当具有的更基本的成分，由此达到在哲学上引起更少困惑的结论。但这恰恰是出问题的地方。如果人们想出一种强到足以回答那些唤起人们询问的最初的哲学问题的分析，那么这种分析似乎复杂和遥远到足够从我们对被分析句子的日常理解中被移除的程度，这样一来，对如下主张的辩护会变得很困难：人们正在做的，就是按照那些句子一直以来被理解的样子来揭示这些句子的内容。另一方面，如果人们的分析紧跟着人们日常的、前哲学的理解，那么这似乎并没有造就任何在本质上足以解决人们最初哲学忧虑的东西。简言之，要么是，人们的分析不会超出自己正在分析的东西，在这种情况下这些忧虑不会消除；要么是，人们的分析将表明，他们可以怎样来解决自己的哲学忧虑，但这只是通过将那种忧虑替换为自己正在分析的新的忧虑。
一般来说，摩尔-罗素分析方法的拥趸们，追随着处理上述问题的两种策略中的一种。策略一涉及对这样论证的尝试，即复杂的、在哲学上有启示性的分析确实给出了如下命题的内容：这些命题一直以来被常识句子表达并为普通人所知——尽管这种分析不为人熟知。某个采取了这种策略的人，以及某个将罗素还原视作提供了一种对算术表达式的真正分析的人，他会坚称，任何知道（3乘以3）加上（4乘以4）=（5乘以5）的人，都已经知道在罗素还原中与这个句子联系在一起的那个命题。根据这种观点，解释关于罗素主义命题的知识是如何可能的，就是解释关于日常算数真理的知识是如何可能的。
策略二是论证，严格来说，普通人不知道，而且从来不知道（3乘以3）加上（4乘以4）=（5乘以5）——而我们现在根据罗素的还原而开始理解这个命题。无可否认，普通人含混和不严密地触及到——或接近——某个可知的，而且实际上是先天可知的东西——即罗素的命题。但是，既然普通人并没有想到那个命题，那么严格来说，我们不能说他或她知道任何先天的东西。这种看待事物方法的支持者们，有时会将他们的分析作为阐释而提及。这种阐释的要点是，提供在哲学上没有争议的的概念，来取代潜在的、有问题的日常概念。在罗素还原的情况下，一个遵循此策略的人会指出，任何可以通过在日常意义上使用数字而完成的理智上的任务，原则上说都可以通过使用罗素的集合论构造来完成；人们不是既需要集合也需要数字。因此，我们通过放弃旧意义上的数字并代之以集合，来简化我们关于共相的概念——由此希望在哲学上获得某种东西。
通常来讲，摩尔-罗素分析方法的拥趸们并不真正清楚地知道，如果要做出一个选择的话，他们希望采取哪种选择。他们知道有一种分析悖论（paradox of analysis），而且他们感到，一定可以对之给出某种解答。但是，他们似乎经常不完全确定这种解答是什么。然而，他们并没有让自己在这一点上的不确定性延缓自己对分析的找寻，或破坏自己对如下事情的信心：这种分析的过程会以某种方式，提供针对他们哲学问题的答案。
(1) 《数学原理》第一卷出版于1910年，第二卷则是1912年，第三卷是1913年，均由剑桥大学出版社出版。罗素关于逻辑主义的著作以伟大的哲学家和数学家戈特洛布·弗雷格的先驱性著作为先导，并受到其巨大影响；弗雷格的开创性作品《算术基础》（Grundgesetze der Arithmetik）的第一卷出版于1893年，第二卷是1903年。
(2) 关于他的计划与辩护问题间关联的逻辑主义观点，这是一种高度简化和初步的概述。到罗素清楚地看到逻辑主义还原将如何进展时，他关于辩护的观点就复杂和细致得多了。请参阅他1907年的文章“The Regressive Method of Discovering the Principles of Mathematics”，reprinted in Bertrand Russell，Essays in Analysis，edited by Douglas Lackey（New York：George Braziller, 1973）。
(3) 对这种版本的逻辑主义的极好的阐发，可以在卡尔·亨普尔（Carl Hempel）的“On the Nature of Mathematical Truth”一文中找到，American Mathematical Monthly，52（1945）：543—556；reprinted in The Philosophy of Mathematics，2nd edition，P. Benacerraf and H. Putnam，eds.（Cambridge：Cambridge University Press, 1983）。
(4) 译者注：此概念相应的英文为“the axiom schema of comprehension”，也被称为“分类公理模式”（axiom schema of specification）、“分离公理模式”（axiom schema of separation）或“子集公理模式”（axiom schema of subset）等。
(5) 那些已经知道罗素悖论的人，或许想了解在此给出的关于后继的定义，该定义假定了一个包含除了z之外所有东西的集合。罗素悖论的教训之一就是，如果人们通过所有东西意指宇宙中完全的所有东西、包括所有集合的话，则不存在这样一个集合。不必担心。一旦类型理论被引入，在后继定义中的Comp（{z}）就会被理解为是，指称了在z层次上除z以外的所有东西且只有这些东西的那个集合（即除了z之外的所有个体的集合）——而且总是会存在这样一个集合。
(6) Bertrand Russell, Introduction to Mathematical Philosophy, 2nd edition, 1920 （London: Allen and Unwin; New York: Macmillan）; reprinted in 1993 （New York: Dover）, pp. 11—12.
(7) 这个论点稍微有些棘手。当被用于一个任意的集合x时，后继的定义并没有说，无论x’的成员w的哪个成员z被从w中消除，人们得到的总会是x的一个成员。它只说，对x’的每个成员w来说，都至少存在一个要素z，它可以被从w中移除而留下的仍是x的一个成员。因此，如果我们将后继的定义用于任意的集合x’和y’，而x’=y’，那么该定义会排除如下可能性：（i）将一个特定的z从x’（y’）的成员w中消除，可能提供给我们一个属于x但不属于y的成员；（ii）将一个不同的z*从w中消除，可能会提供给我们一个属于y但不属于x的成员。当x’（也即y’）是一个自然数时，这种可能性被排除了，就像在A4中所假定的那样。尽管从直觉上很容易看出这点，但在一种充分严格和形式化的证明中，我们还需要证明这一点。尽管这是可能的，但我们在此不会深究其细节。
(8) 译者注：原作中编号误为（iv）。
(9) 尽管这是可以在形式上加以证明的，但我们仍然不会深究其细节。
(10) 参阅Introductio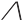
to Mathematical philosophy第13章，pp.134—143。
(11) 我用xn作为x拥有n个下标“i”的方便的缩写。
(12) 译者注：原作中“Niiii”误为“Niii”。
(13) Carl Hempel，“On the Nature of Mathematical Truth”，American Mathematical Monthly 52（1945）：543—556；reprinted in The Philosophy of Mathematics，Benacerraf and Putnam，eds.。引文出自后者。
(14) 同上，第374页，着重号为本书作者所加。
(15) 在《论数学真正的本质》第375页的脚注9中，亨普尔暗示说，关于上述相关词项的“通常意义”，他所想到的是所谓“‘意义（meaning）’的逻辑含义（sense）”，而非“心理学含义”。这个区分所产生的问题，只被亨普尔简要地概述，我们将在随后对此加以讨论。
(16) 《论数学真正的本质》第378页，着重号为本书作者所加。
(17) 参阅“The Regressive Method of Discovering the Premises of Mathematics”，1905，in Bertrand Russell，Essays in Analysis，Douglas Lackey，ed.（New York：George Braziller, 1973）。
(18) Ibid.，pp. 282—283.