第五章 逻辑形式、语法形式和摹状词理论
本章概要
1．摹状词理论的背景
否定存在句的问题；逻辑形式和罗素解决方案背后的考虑
2．罗素的形式化语言及其解释
3．对否定存在句的分析
罗素对否定存在句问题的解决方案；摹状词理论，作为缩写摹状词的语法专名，以及逻辑专名的本质
4．罗素用于决定包含摹状词句子的逻辑形式的规则
罗素理论的适用范围
歧义和排中律
摹状词的域（scope）
域，命题态度句，以及关于乔治四世和《威弗利》（Waverley）作者的难题
5．罗素的认识论与摹状词理论间的冲突
亲知的知识，描述的知识；罗素关于逻辑专名和命题态度归属句（propositional attitude ascriptions）中量词化的限制
6．语言分析和形而上学实践
用罗素主义的分析，来阻止关于疯长的本质论（rampant essentialism）和绝对唯心论的论证
伯特兰·罗素和G. E.摩尔是相互给予对方重要影响的同侪，特别是在各自职业生涯的早期。十九世纪末，他们作为学生在剑桥相遇，并且都开始了哲学之外领域的研究。摩尔起初对古典学的研究怀有浓厚兴趣，随后在罗素的劝说下转向哲学；而罗素自己则是数学专业的本科生，对哲学的最初兴趣始于对数学的哲学基础的关注，他也将自己职业生涯的早期奉献在了这个领域。而罗素最具影响力的贡献之一，便是他在符号逻辑领域内的开拓性工作。但是，他并未局限于技术性的问题。相反，他的目标是，将在数学中发现的严格和科学的精神，带到数学哲学乃至所有哲学中去。这个目标的核心在于，将逻辑中特定的结论和技术用于攻克传统的哲学问题。
摹状词理论的背景
这些技术中最重要的一项，便是对其摹状词理论的使用。为了理解是什么引导罗素走向这种理论，人们必须了解一些他发展这种理论的哲学背景。在罗素和摩尔最初开始对哲学感兴趣的时代，在剑桥大学占统治地位的思想流派是绝对唯心论，他们在剑桥的一位老师约翰·麦塔格特（J. M. E. Mctaggart）正是此流派的主要拥趸之一。这个流派的哲学家坚信，所有的实在都是精神性的——这使得他们成为唯心论者。他们也坚信，实在的整体是单个统一（single unified）的对象，要么是一个神性的心灵，要么（据唯心论者说）是一个由相互依赖的诸心灵构成的整体系统——这就是他们为什么是绝对唯心论者的原因。导致这种整体图景的观念之一，便是被称作内在关系的实在性原则（the doctrine of the reality of internal relations）的东西。在最极端的形式中，这条原则坚信，任何一个对象的本质和存在都如此地依赖于所有其他对象的本质和存在，以至于任何实体（entity）只要损失了哪怕自己实际拥有的任何一项单一的属性，宇宙自身或其任何部分便都不会存在。尽管这种观点令人惊讶而且显然违背我们的日常思维方式，但唯心论者给出的论证在一定程度上是可接受的，而且（如我们接下来将看到的那样）并非完全让人感到索然无味。
在学生时代，摩尔和罗素一度受到他们老师的唯心论观点的影响。然而，他们很快就由摩尔带领着进行了反叛。摩尔一些最令人感兴趣的文章——比如，《对唯心论的反驳》（The Refutation of Idealism）和《外在与内在关系》（External and Internal Relations）——对唯心论的核心原则提出了清晰而有力的批评。(1)在很早的时候，摩尔对绝对唯心论的反驳，将他导向一种观点的极端版本，即哲学实在论（philosophical realism），但更合适的名称是哲学多元论（philosophical pluralism）。罗素也追随他坚持这种观点。
摩尔和罗素早期的实在论，由三条基本的本体论承诺构成。首先是对日常对象——人类、身体、物理对象等——存在的信念。最初，摩尔和罗素都没有倾向于说，在实在中不存在我们一般所设想的事物，而只有由其他更基本的元素构成的各种各样的星座一样的东西。他们的第二条实在论承诺是，相信数学和逻辑实体的存在，比如数、集合、关系和性质——大致相当于哲学家所谓的“抽象对象”。如他们所言，他们早期实在论的第三条承诺是，相信“思维的所有对象”必定具有某种存在性（因为否则的话我们不能思考它们）。根据这条信念，人们可以思考珀加索斯（Pegasus）(2)、圣诞老人和当今的法国国王这种事实说明，它们必须具备某种存在性，因此它们是实在的真实的组成部件。
这三条本体论承诺是摩尔和罗素最初所采取的立场，但接下来就被修正或抛弃了，而这次是罗素带的头。到最后，在对它们的批判上，罗素比摩尔走得更远，并最终拒斥了这些观点所表达的大部分内容。此种背离哲学多元论的运动，为这种观点——哲学是分析——的更新、更彻底的解释铺平了道路，也为随后的逻辑原子主义和逻辑实证主义学派奠定了基础。我们将追踪罗素在这条道路上的进展，并以他在这个方向上的第一步，即他的摹状词理论的发展为起点。
这种理论构成了他对下述观点拒斥的核心：思维的所有对象一定具有某种存在性，因此珀加索斯、圣诞老人和当今的法国国王之类的东西必定存在。支持这条原则的关键论证，建基于被称为否定存在句的陈述。罗素写于1900年、发表于1903年的早期著作《数学原则》给出了这种论证。(3)
在全书开始的部分，罗素解释了一些关键术语，并期待在接下来给出基于否定陈述的论证。
任何可能作为思维的对象，或可能出现于真或假的命题中，或可以被计数为一的东西，我都将之称为一个项……一个人，一个时刻，一个数字，一个类，一组关系，一只奇美拉（chimera），或其他任何可以被提到的东西，必定都是一个项；而否认如此这般的事物是一个项，则一定是错误的。(4)
罗素在这本著作的随后部分这样陈述该结论的论证：
存在是这样的东西：它属于所有可设想的项，属于所有可能的思维对象——简言之，属于所有可能出现于无论真假的任何命题中的东西，也属于所有这些命题自身。存在属于任何可以被计数的东西。如果A是任意一个可以被计数为“一”的项，那么显然A是件什么东西，而且因此A是其所是。“A不是其所是（A is not）”一定总为假或无意义。因为如果A什么都不是，那么就不能说它什么都不是；“A不是其所是”暗含了存在着这样一个项A，它的存在被否定了，而因此A是其所是。那么，除非“A不是其所是”是一声空洞的声响，它一定为假——无论A可能是什么，情况一定如此。数字、荷马史诗中的诸神、关系、奇美拉和四维空间，它们都具有存在性，因为如果它们不是某种实体，我们就不能制造出关于它们的命题。所以，存在是所有事物的一般属性，而无论谈及任何事物都会显示这一点。(5)
在检验罗素立场的时候，我们要首先重构关于他似是而非的结论的论证，然后展示他随后如何用自己的摹状词理论，来阻止这条有问题的结论。这种论证建基于否定存在句，为了当前的目的，我们可以认为否定存在句包含了（a）或（b）中的任何一个。
a．x不存在。
b．诸x不存在。
下面的（1）—（3）是否定存在句的例子。
1．食肉的奶牛（Carnivorous cows）不存在。
2．黑湖怪兽（The creature from the black lagoon）(6)不存在。
3．圣诞老人不存在。
考虑到这些例子，罗素1903年的论证可以被重构如下：
P1．有意义的否定存在句，比如（1）—（3），是主谓句。例如，（1）的主语是食肉的奶牛，而谓语是不存在。
P2．一个有意义的主谓句为真，当且仅当有一个（或一些）主词表达式所指涉的对象，并且这个对象具有（或这些对象具有）谓词所表达的属性。
C1．句子（1）可以为真，仅当有它的主词表达式——食肉的奶牛——所指涉的对象——食肉的奶牛，并且这些对象具有不存在这种属性。对（2）（3）和所有其他有意义的否定存在句来说都是如此。
P3．没有对象具有不存在这种属性。如果有有意义的否定存在句的主词所指涉的对象，那么它们就存在。
C2．有意义的否定存在句不可能为真。
C3．因此，没有为真的、有意义的否定存在句。
C4．换言之，为真的、有意义的否定存在句不存在。
C4本身既是一个有意义的否定存在句，又是P1—P3的逻辑后承。既然这些前提蕴涵了这样一种一般性的断言——它是自身的一个反例，那么它们中至少有一个为假。问题在于，究竟是哪一个。1903年，罗素原初的“实在论”（或“多元论”）解决方案，将困难锁定在P3上。根据他那时所持的观点，存在性是有等级的，其中包括一个不存在的事物的范畴，这些事物具有的存在性，比那些存在的事物所具有的存在性等级更低。根据这种观点，确实有诸如食肉的奶牛、最大的质数、单词philosophy中的字母“f”、当今的法国国王、金山甚至实存的金山这样的事物。有这样一些事物，它们具有存在性，尽管它们并不存在。它们与那些真正存在的事物相对，比如英国女王、唯一的偶数质数和维苏威火山。如罗素所说：“存在性是所有事物的一般属性，而谈及某物就是去显示存在性是什么。相反，实存（Existence）只是其中一些存在物的特权。”(7)
尽管罗素最初受到这种观点的吸引，但他很快便将其视作不可思议的。到1905年，他已经把它归于另一位哲学家——迈农（Meinong），并以下述方式对之进行了批评：
这种理论，将任何一个语法上正确的指谓性短语（denoting phrase），当作代表一个对象。因此，“当今的法国国王”“圆的方”等诸如此类的东西，都应当是真实的对象。我们承认这些对象并不存活（subsist），可它们应当是对象。这种观点本身包含困难；但首要的反驳是，这种对象无疑倾向于违反矛盾律。例如，这种观点主张：实存的当今法国国王既存在又不存在；圆的方既是圆的又不是圆的，等等。这是不可容忍的；而且如果可以发现任何一种理论来避免这种结果，自然是再好不过了。(8)
数年后，在著作《数理哲学导论》（Introduction to Mathematical Philosophy）（写于他因反对一战而入狱期间，并于1919年首次出版）里名为“摹状词”的一章中，罗素表达了对自己1903年观点的反驳：
由于缺乏一种命题函项的工具（apparatus）（罗素1905年摹状词理论的核心特征），许多逻辑学家被导向这样一种结论：有不真实的对象。例如，迈农论证说，我们可以谈论“金山”“圆的方”等等；我们可以制造出以它们为主词的真命题；因此，它们必定具有某种逻辑上的存在性，否则它们出现于其中的命题就是无意义的。在我看来，这些理论有一种对实在的感受的缺失，而这种感受即使在最抽象的研究中也应当被保有。我坚持认为，逻辑必须像动物学那样不承认独角兽；因为逻辑关涉的是像动物学一样真实的现实世界，即使逻辑拥有更抽象和更一般的特性。说独角兽在徽章上、在文学里或在想象中具有某种存在，这是一种最可悲、最微不足道的借口。在徽章上存在的并不是一只由肉和鲜血组成、自发地移动和呼吸的动物。存在着的是一幅图画或语词中的一个摹状词。同样，例如坚持哈姆雷特存在于他自己的世界——莎士比亚想象的世界——与（说）拿破仑存在于日常世界一样真实，这就等于在说某种刻意迷惑人的东西，或是在某种程度上几乎不可信的胡话。只有一个世界，“真实的”世界：莎士比亚的想象是它的一部分，而他在写哈姆雷特时所具有的想法是真实的。我们在阅读这部剧时所具有的想法也是如此。虚构作品的本质在于，只有莎士比亚和读者的想法、感觉等才是真实的，除这些之外，没有一个客观的哈姆雷特。当你考虑到作家和历史读者被拿破仑所唤起的所有感觉时，你并没有接触到那个实际的人；但在哈姆雷特的情形下，你已经穷尽了关于他的所有事情。如果没有人想到哈姆雷特，那么也就没有关于他的任何事情存留；如果没人想到拿破仑，一旦有人想起他时，他就又会立即浮现出来。(9)
显然，罗素彻底拒斥了极端的“实在论”观点，这种观点最初由他在1903年涉及否定存在句的论证所支持。正是1905年《论指谓》中的摹状词理论允许他这样做。这种理论和他对自己早先论证拒斥的核心在于他关于逻辑形式和语法形式的著名区分。在罗素看来，句子表达思想或命题。就像句子拥有一个语法形式那样，句子所表达的命题（思想）则拥有一个逻辑形式。有时，S所表达的命题的逻辑形式与S的语法形式相一致，有时则不然。如果S在语法上具有主谓形式，并且它所表达的命题的逻辑形式与S的语法形式相一致，那么S就被称作在逻辑上拥有主谓形式。这种情况适用于S所表达的命题P可以被完全地划分为如下两个部分的情况：（i）谓词所表达的属性，（ii）与S的语法主词相应的成分。现在，关于这个成分是否是主词表达式的指称（referent）或一个决定了主词指称的概念的问题，我们保持开放。（最终罗素会坚持它一定是这个指称，但我们现在无需坚持这点。无论在何种情况下都应这样理解：谓词所表达的属性就是要被用来谓述主词表达式的指称。）S的逻辑形式（换言之，S所表达的命题）在决定S于何种条件下为真时，扮演了重要角色。
考虑到这些，涉及否定存在句的悖论可以被这样重新表述：
P1a．有意义的否定存在句，比如（1）—（3），在逻辑上具有主谓形式。
P2a．一个在逻辑上拥有主谓形式的句子为真，当且仅当有一个（或一些）主词表达式所指涉的对象，并且这个（或这些）对象拥有谓词所表达的属性。
C1．句子（1）可以为真，仅当有它的主词表达式——食肉的奶牛——所指涉的对象——食肉的奶牛，并且这些对象具有不存在这种属性。对（2）（3）和所有其他有意义的否定存在句来说，都是如此。
P3．没有对象具有不存在这种属性。如果有有意义的否定存在句的主词所指涉的对象，那么它们就存在。
C2．有意义的否定存在句不可能为真。
C3．因此，没有为真的、有意义的否定存在句。
C4．换言之，为真的、有意义的否定存在句不存在。
罗素1905年对这个版本悖论的解决方案是否定P1a。尽管像（1）—（3）这种否定存在句在语法上拥有主谓形式，但他主张，其所表达的命题（思想）并不是这样。他的策略是，为每一个有问题的否定存在句S制造一个逻辑上等价的、不拥有主谓形式的句子S1——在此S1的语法结构映照出S和S1所表达的命题的逻辑结构。在否定存在句C4的情形下，相应的改写可能是C3或C2。在否定存在句（1）的情形下，其改写则可能是沿着（4）这条路线的某种东西。
4．所有事物都是这样：要么不是奶牛，要么不是食肉的。
当考虑（4）时，我们看到该句子中没有任何一部分指涉了以前被说成是不存在的东西。因此，宣称它为真就不包含任何悖论。最终，如果句子（1）表达了与（4）同样的命题，那么它的真也就不包含悖论。
为了将这种方案一般性地扩展到否定存在句，同其他在哲学上有问题的句子一样，还需要两样东西。第一，我们需要某种关于句子所表达的命题（思想）的逻辑形式的构想，以及某种清晰明确地表现该形式的方法。第二，我们需要某种精确和系统的方法，将一个日常英语中的句子的逻辑形式从其明显的语法形式中抽取出来。这二者都由罗素的摹状词理论提供，我们将分三步展示它。首先，我们会定义一种表现逻辑形式的简单形式化语言，在其中句子的语法形式映照出句子所表达的命题（思想）的逻辑结构，并且我们会对此提供一种罗素主义的解释。接下来，我们会检验，罗素如何使用他的形式化语言去提供一种关于有问题的否定存在句的分析。最后，我们会展示，关于将包含各种名称和摹状词的日常英语句子翻译成形式化语言中的句子——这些句子（据说）表达了与原初的英语句子同样的命题（思想）——的罗素主义原则。
罗素的形式化语言及其解释
为了详述这种形式化语言，我们首先展示一下它的基本词汇，然后展现如何用这些词汇构造句子。沿着这条路径，我们会引入一种作为语法范畴的式子的观念，它是词汇和句子的中介。只有句子才（独立地）表达完整的思想或命题。
形式化语言
Ⅰ．词汇
1．谓词
=，A，B，C，……（这些谓词被分为一元的，二元的，……n元的。一元谓词，比如是红色的，表达个体的性质；二元谓词，比如比……重，表达一对个体之间的关系；以此类推。一个n元谓词在语法上与n个词项结合在一起，形成一个式子。）
2．词项（这些表达式标示或指涉单一个体）
a．变量
x，y，z，x’，y’，z’……
b．名称
x，y，z，x’，y’，z’，……（通俗地讲，在变量下加上下划线，会涉及将其处理为一个名称。）
Ⅱ．式子
1．原子式
一个为n个词项所跟随的n元谓词是一个原子式（在“=”的情况下，我们让词项排列在谓词两侧而不是跟随在它之后。）
2．其他式子
如果Φ和Ψ是式子，那么～Φ，（ΦvΨ），（Φ&Ψ），（Φ→Ψ）和（Φ↔Ψ）都是式子。如果v是一个变量而Φ （v）是一个包含了v的出现的式子，那么∀v Φ（v）和∃vΦ（v）都是式子。（在不产生歧义的情况下，有时可以去掉圆括号。）
～Φ被读作或读成非Φ，是Φ的否定；（ΦvΨ）被读作或读成Φ或Ψ，是Φ和Ψ的析取；（Φ&Ψ）被读作或读成Φ且Ψ，是Φ和Ψ的合取；（Φ→Ψ）被读作或读成如果Φ则Ψ，是以Φ为前件和以Ψ为后件的条件式；（Φ↔Ψ）被读作或读成Φ当且仅当Ψ，是联结Φ和Ψ的充分必要条件式；∀v Φ（v）被读作或读成对所有v而言，Φ（v），是Φ（v）的全称概括（universal generalization）；而∃v Φ （v）被读作或读成至少有一个这样的v，Φ（v），是Φ（v）的存在概括（existential generalization）。∀v和∃v被称作量词。
Ⅲ. 句子
1．一个句子是一个不包含变量的自由出现的式子。
2．一个变量的自由出现
一个变量的出现是自由的，当且仅当它不是被约束的。
3．诸变量的约束出现
一个变量在式子中的出现是被约束的，当且仅当这种出现是在量词的域内对这个变量的使用。
4．一个量词∀v或∃v出现的域
一个量词在式子中的出现的域，是该量词加上紧随其后的（最小的完整的）式子。
Ⅳ．例子
∀x（Fx →Gx）和∃x（Fx &Hx）都是句子，因为附属于量词的“x”在式子中的两次出现都在该量词的域内。请注意，在这些句子中（i）由于“（”的介入，Fx并不直接跟随在量词之后，（ii）（Fx并不是一个完整的式子，因为它包含“（”而没有“）”相随。相比之下，（∀x Fx →Gx）和（∀x（Fx & Hx）→Gx）不是句子，因为跟随着“G”的“x”的每次出现都是自由的。
对这种语言的罗素主义解释
Ⅰ．命题和命题函项
句子表达命题。不是句子的式子（“开放式句子”）表达命题函项。一个命题函项是这样一种函项：将命题作为值，赋予作为变量的对象。例如，如果用谓词“C”意指“是一头奶牛”，那么式子“Cx”就表达这样一种函项：对任意一个作为变量的对象o，该函项都将一个命题作为值赋予它，这条命题论及o是一头奶牛。这条命题为真，当且仅当o是一头奶牛，而且被“Cx”——其中“x”命名了o——所表达。
Ⅱ．真理
1a．被句子∀v Φ（v）表达的命题为真，当且仅当被Φ（v）表达的命题函项，对v的所有的值来说都为真——也就是说，当且仅当，对每个作为变量的对象o，该函项都将一个关于o的真命题作为值赋予它。当且仅当对每一个对象o而言，将所有v的自由出现都用于命名o，而由此产生的结果Φ（v）都表达了一个真命题时，情况就是这样。
b．被句子∃v Φ（v）表达的命题为真，当且仅当被Φ（v）表达的命题函项至少对v的一个值为真——也就是说，当且仅当至少有一个这样的对象o：当上述函项被用于作为变量的o时，该函项将一个真命题作为值赋予它。当且仅当至少有在一个这样的对象o——将所有v的自由出现都用于命名o，而由此产生的结果Φ（v）都表达了一个真命题——时，情况就会是这样。
2a．被句子～Φ表达的命题为真，当且仅当被Φ表达的命题不为真。
b．被句子（ΦvΨ）表达的命题为真，当且仅当或者被Φ表达的命题为真，或者被Ψ表达的命题为真。
c．被句子（Φ&Ψ）表达的命题为真，当且仅当被Φ表达的命题为真，并且被Ψ表达的命题为真。
d．被句子（Φ→Ψ）表达的命题为真，当且仅当情况不会是（被Φ表达的命题为真，并且被Ψ表达的命题为假）。
e．被句子（Φ↔Ψ）表达的命题为真，当且仅当被Φ表达的命题和被Ψ表达的命题都为真或都为假。
3．谓词代表性质（或关系）。名称代表对象。一个原子句由名称加上一个单称谓词构成。被这样一个句子表达的命题为真，当且仅当被命名的那个（或那些）对象具有被谓词所标示的性质（或具有被谓词所标示的关系）。例如，如果“C”代表的是一头奶牛这个性质，那么被原子句“Cx”表达的原子句为真，当且仅当被“x”命名的对象是一头奶牛。每一个不为真的命题都为假。
命题结构
最后，我们来简述罗素关于命题结构的理论。根据他的看法，命题可以算作被句子编码的信息。他把被一个（在一种逻辑上完美的语言中的）句子编码的信息当作一种复合实体，该实体的结构映照出该句子的结构。被他的形式化语言中的句子所表达的命题，以如下方式被确定。
I．被由一个为n个名称跟随的谓词构成的原子句Pt1……tn表达的命题，是〈P*，O1……On〉这样一个复合物，它由被该谓词表达的性质（或关系）加上这些名称的指称构成。
一个包含某个变量的一次或更多次自由出现的原子式Pt1……tn，其本身并不表达一个命题。但是，相对于关于对象的赋值——这种赋值将对象作为原子式中自由变量的（临时）指称——而言，这样一个原子式确实表达了一个命题。因此，相对于将对象赋予其自由变量的赋值A而言，被Pt1……tn表达的命题，是〈P*，O1……On〉这样一个复合物，它由被该谓词表达的性质（或关系）加上这些项与A相关的指称构成（只当变量在式子中自由出现时，A才是与此有关的）。这种命题为真，当且仅当这个（或这些）对象具有P*这种性质（或处于P*这种关系中）。
II．被式子～Φ（相对于赋值A而言）表达的命题是〈Neg，Prop Φ〉这样一个复合物，其中Prop Φ是被（相对于A而言）Φ表达的命题，而Neg是这样一种性质：是一个非真的命题。〈Neg，Prop Φ〉为真，当且仅当Prop Φ不为真。
III．被式子（Φ&Ψ）（相对于赋值A而言）表达的命题是〈Conj，Prop Φ，Prop Ψ〉这样一个复合物，其中PropΦ和Prop Ψ是被Φ和Ψ所表达的命题，而Conj是当且仅当一对命题都为真时，二者之间所存有的关系。因此，〈Conj，Prop Φ，Prop Ψ〉为真，当且仅当PropΦ和Prop Ψ都为真。类似的规则规定了被（Φ v Ψ），（Φ→Ψ）和（Φ↔Ψ）表达的命题。
IV．被式子∃v Φ（v）（相对于赋值A而言）表达的命题是〈SOME，g〉这样一个复合物，其中g是这样一种命题函项：相对于一种赋值A’而言，它将一个被Φ（v）表达的命题赋予每个对象o，其中A’将o赋值为v的指称（否则就与A等同）；而SOME是这样一种性质：是一个“有时为真”的命题函项。（即将一个真命题赋予至少一个对象）因此，〈SOME，g〉为真，当且仅当至少有一个对象“是Φ”。
被式子∀v Φ（v）（相对于赋值A而言）表达的命题是〈ALL，g〉这样一个复合物，其中g是这样一种命题函项：相对于一种赋值A’而言，它将一个被Φ（v）表达的命题赋予每个对象o，其中A’将o赋值为v的指称（否则就与A等同）；而ALL是这样一种性质：是一个“总是为真”的命题函项。（即将一个真命题赋予每一个对象）因此，〈ALL，g〉为真，当且所有对象都“是Φ”。(10)
对否定存在句的分析
基本想法
考察了罗素关于命题结构的想法和他用于呈现它们的形式化语言后，现在我们处于这样的位置：要去理解他如何将这些想法运用于否定存在句的悖论。在发展摹状词理论的时候他开始考虑，这种悖论出自：未经批判地将语法形式当作逻辑形式的精确指标。句子α不存在在语法上具有主谓结构的形式。我们时常假定，如果一个句子是主谓结构的，那么它就在如下情况下为真：当且仅当主语表达式指涉某个事物，该事物具有被谓语表达的性质。在否定存在句的情况下，这就意味着，该陈述为真，当且仅当α指涉一个不存在的对象。但这似乎是荒谬的，因为似乎如果有α指涉的某物，那么它必定存在。
罗素开始相信，破解这条悖论的方法就是，认清这种句子的逻辑形式
1．食肉的奶牛不存在。
得自（a）这种东西。
（a）∀x（～ Cx v ～ Mx）
在此，我们用“C”代表是一头奶牛这种性质，而“M”代表是食肉的这种性质。如此一来，被（a）表达的命题就由如下东西构成：ALL这种属性，加上将这种命题——该命题说o要么不是奶牛要么不是食肉的——赋予每个对象o的命题函项g。因此，罗素将（a）当作是说出了某种大致可以在英语中被改写为（b）或（4）的东西。
（b）将这种命题——要么不是奶牛要么不是食肉的——赋予每个对象o的命题函项，总是为真的。
4．所有事物都是这样：要么不是奶牛，要么不是食肉的。
这就是他所认为的更容易被（1）的表达所误导的东西。他相信，一旦我们看到了这点，就不再会试图认为，只有当真的有这样一些被其语法主语指涉、具有不存在性质的对象——食肉的奶牛——时，（1）才会为真。
将这种分析扩展到涉及单称限定摹状词的情况
我们的下一步是将这种分析扩展到其他否定存在句，比如（2）。
2．黑湖怪兽不存在。
（2）和（1）的不同之处在于，它拥有一个单数主语。在考虑罗素会如何处理这个句子时，让我们看一下相应的肯定存在句。
5．那只黑湖怪兽存在。
为了方便起见，我们让“C”代表是一只怪兽（is a creature），而“B”代表黑湖（is from the black lagoon）。出于这种考虑，请考虑（6）这种逻辑表述。
6．∃x（Cx & Bx）
在罗素看来，（6）为真，当且仅当被（Cx and Bx）表达的命题函项对“x”的至少一个值为真。换言之，（6）为真，当且仅当至少一个对象是黑湖怪兽。但是，应当注意的是，这并不就是（5）所告诉我们的东西。（6）在可能有很多黑湖怪兽的问题上保持开放。然而，在（5）中对定冠词那只的使用，似乎暗示应当只存在着一只这种怪兽。(11)我们需要在罗素的形式化语言中找到一种表达这一点的方法。像我们将会看到的那样，有几种不尽相同但在逻辑上等价的方式来做到这一点。
首先，请考虑式子（7），在其中“x”是我的名字——司各特·索姆斯。
7．∀y（（Cy & By）→ y=x）
这个句子说，如果一个对象是一只黑湖怪兽，那么它就是我。这与两种不同的可能性相容：（i）没有对象是黑湖怪兽。（ii）准确来说，有一个对象是这种怪兽，那就是我。第一种可能性被（8a）排除了，（8a）与（8b）等价。
8a．∀y（（Cy & By）↔ y=x）
b．∀y（（Cy & By）→ y=x）&∀y（y=x→（Cy & By））
这些句子为真，当且仅当所有对象都满足两个条件：（i）如果它是一只黑湖怪兽，那么它就是我，（ii）如果它是我，那么它就是一只黑湖怪兽。既然我是一个对象且与自己等同，那么只有当我是一只黑湖怪兽时，我才满足第二个条件。因此（8a）和（8b）可以为真，当且仅当我是这样一只怪兽。现在请考虑所有其他对象。除了我以外没有对象与我等同。那么，只有当这些对象不是黑湖怪兽时，它们才满足第一个条件。因此，（8a）和（8b）为真，当且仅当我——司各特·索姆斯——是一只且是唯一的那只黑湖怪兽。
现在请考虑（9）。
9．∃x∀y（（Cy & By）↔ y=x）
存在一个对象x，对无论任何对象y来说，x与y等同，当且仅当y是一只黑湖怪兽。
这个句子为真，当且仅当存在一个对象，它是一只且是唯一的那只黑湖怪兽。（8a）和（9）之间唯一的不同之处是，（8a）告诉我们，准确来说哪个对象满足这种描述——那就是我。（9）则告诉我们，有一个且只有一个这样的对象，但并没有鉴别出它。因为（5）这个英文句子说有这样一个对象，但并没有鉴别出它，所以罗素认为（9）表达了（5）所表达的东西。
此前我曾提到，有几种不尽相同但在逻辑上等价的方法，来使用我们的罗素主义语言去表达（5）所表达的东西。（9）是其中一种方法。另两种方法由（10）和（11）给出。
10．∃x（Cx & Bx）&∀y∀z ［（（Cy & By）&（Cz & Bz））→ y=z］
至少有一个事物是黑湖怪兽，而且对每一对对象来说，如果二者都是黑湖怪兽，那么它们就是等同的——换言之，至少有一只黑湖怪兽，而且至多有一只黑湖怪兽。
11．∃x ［（Cx& Bx）&．y（（Cy& By）→ y=x）］
至少有一个事物，它既是黑湖怪兽，又与任何是黑湖怪兽的东西等同。
为了罗素的目标，（9）（10）和（11）中的任何一个句子都会作为被（5）表达的命题的表现而起作用。一个问题是，他从未清楚地讲明，（9）（10）和（11）是否都表达了同样的命题，或者它们是否表达了结构上不同但逻辑上等价的命题。一般而言，既然罗素没有鉴别出逻辑上等价的命题，那么他主张（9）（10）和（11）表达了逻辑上等价的不同命题，就是很自然的了。但这样一来人们会问，这其中的哪个命题是（5）在英语中真正表达的呢？
罗素从未回答这个问题，而且我也不会回答。但是，我们可以注意两点：（i）出于提供一种对否定存在句的分析的目的，我们选择哪一个句子是无所谓的。任何一个句子都允许我们避免（2）这种句子所造成的悖论。（ii）既然（9）是所使用的最简单的句子，而且罗素经常运用它，那么我们可以认为它与（5）表达了相同的命题。
现在我们有了一种对（5）的罗素主义分析，而这是一种肯定存在句，对相应的否定存在句（2）的分析自然如下。
12．～∃x∀y（（Cy & By）↔ y=x）
这个式子说，情况不是这样的：准确来说有一个对象是黑湖怪兽，或者用同样的话说，任何一个对象，要么不是黑湖怪兽，要么是众多黑湖怪兽中的一个。在罗素看来，这就是（2）表达的内容。
英语句子（2）及其罗素主义逻辑形式（12）之间的关系，被认为是像关于食肉奶牛的英语句子（1）及其逻辑形式（4）之间的关系。（1）乍看上去似乎指涉了一些事物并说它们不存在，同样，（2）乍看上去似乎也指涉了一个单独的事物并说它不存在。在这两种情况下，罗素通过这种方式——在其中没有涉及任何关于非存在的所指（reference）或谓词——分析被表达命题的逻辑结构来解决该悖论。
将这种分析扩展到涉及语法专名的句子
接下来要考虑的那一类否定存在句，是像（3）一样的句子，其语法主语是日常专名。
3．圣诞老人不存在。
尽管这个句子为真，但其中包含着与我们之前的例子相同的迷惑。不足为奇的是，罗素对关于（3）这种迷惑的解决，与他对之前情况的解决相似。
在罗素看来，当我们使用一个像圣诞老人这样的专名时，我们总是在心中有一些这样的描述：在暗示这个名字应当被如何使用时，我们会准备好提供这些描述。究竟哪种描述给出了这个名称的内容，因人因时而异。但是，无论（3）何时被使用，总是存在某种可以代替它的描述。因此，当我们使用（3）时，总是用它意指某种（3a）这样的东西。
3a．那个生活在北极以及……的老人不存在。
但既然（3a）有这种结构
3b．那个如此这般之物不存在。
罗素就可以用他对限定摹状词的分析来给出被（3）表达的命题的逻辑形式（3c）。
3c．～∃x∀y（y is so and so↔y=x）(12)
结果，根据罗素的分析，（3）的真并不要求任何对象具有不存在这种性质，上述悖论也就得到了解决。
逻辑专名
对（3）分析的关键就是最初的那一步——主张圣诞老人只是一个特定的摹状词短语的缩写，该短语反过来可以被罗素依据量词、逻辑符号和谓词加以分析。根据这种观点，即使日常的专名在逻辑上也并不像名称那样起作用。也就是说，它们的功能并不仅仅在于标记或直接指涉任何事物。但如果情况是这样，那么人们可能想问，名称这个概念是否还在罗素关于逻辑形式的设想中起任何作用。我们可以换一种方式说。在英语中是否存在任何这样的语词，其逻辑功能不是代替摹状词，而只是标记或指涉某个对象？
罗素认为，至少存在一个这样的词——这个（this）。请考虑如下例子：我举起自己的钱包并说这个是空的。在此，语词“这个”的功能仅仅在于标记或指示我在谈论的东西。如果我的钱包不在手上，那么我不会简单地说这个是空的，因为我的听众可能不知道我在说什么。在那种情况下，我会使用我平日里携带的那个钱包这样一个摹状词来让他们理解我的意图。但是，在钱包在我手上的情形下，我无需这样做，因为他们完全可以看见我在谈论什么。在此，语词“这个”并不作为一个摹状词起作用，而是一个关于我所谈论东西的赤裸的标签。
涉及“这个”的否定存在句在表面上的荒谬性，是支持这种观点的一件事情。
13．这个不存在。
如果我说出（13），并将我的注意力指向某物，或对它做出手势，那么我的评论会很难被理解。我对指示词“这个”的使用，加上我的手势，会暗示我自己在指涉某物。但这样一来我会处于一种奇怪的立场，即意图指涉某个我接下来就说其并不存在的东西。因此，罗素的确认为，（13）是那种匪夷所思的、罕见的否定存在句的情况：诚挚地使用它就假定了它不可能为真。罗素以此来暗示，对（13）的分析与对之前例子的分析不同。在（13）这种情况下，句子的语法主语的功能仅仅是命名某物，而不是去描述它。他通过如下说法表达这一点：“这个”是一个逻辑专名。
我会加入一种迄今并未被引入的复杂化因素。它涉及如下问题：何种对象可以是逻辑专名的指称？到目前为止，在我的谈话中，像我钱包这样的物理对象好像可以是逻辑专名的指称。事实上，罗素对此半信半疑，并最终否定了这一点，取而代之的是如下观点：人们可以命名为逻辑专名的，只能是自己的感觉印象、思想或其他自己以最直接的方式亲知的东西（比如抽象性质和关系）。因此，当这个被用作一个逻辑专名时，它总是命名了上述那些对象中的一个；任何其他的使用都只能被当作这样：它像被隐藏起来的摹状词那样起作用。
至少罗素关于这个问题的部分推理可以重构如下：首先，我们来定义逻辑专名的概念。
定义：逻辑专名
一个逻辑专名是这样一个词项：其意义就是其指称。
为了论证的需要，接下来让我们假定，关于是否用自己的语词意指某物，人们是不会犯错的。当我使用一个表达式时，似乎经常可以确定自己用它意指某物，即使我可能并不确定自己用它意指的东西与别人用它意指的东西是否相同，或者当该表达式在以我赋予其上的意义被使用时是否真正指涉任何事物。在这些情况下，我可以确定自己用该表达式意指某物，即使我并不确定它是否成功地指涉了世界中的任何东西。例如，我可以确定，当自己使用语词我在普林斯顿拥有的那栋房子时，自己意指某物，即使我并不完全确定该表达式指涉任何东西，因为，至少可能的是，在我离开自己的房子后它被烧毁了。同样，罗素会说，就像我在使用日常名称圣诞老人——即使它并不指涉任何事物——时意指某物一样，我也可以确定自己在使用名称柏拉图时意指某物，即使我并不完全确定是否真的存在这样一个人。罗素会通过如下说法表达这一点：（i）语法专名圣诞老人在被我使用时有某种意义，即使它没有指称，（ii）我可以知道，语法专名柏拉图在被我使用时有某种意义，即使我并不知道它有指称。
现在假设，某个表达式N被我用作一个逻辑专名——也即用作一个其意义就是其指称的表达式。这样一来，人们可能会争论说，无论我何时诚挚地用N去意指某物时，N都如我所使用的那样去意指和指涉某物。这是有保障的，因为无论我何时诚挚地用N去意指某物时，它都确实意指某物，而且它所意指的东西就是它所指涉的东西。此外，它所意指和指涉的那个东西，就是我用它所要意指和指涉的东西。因此，可以作为逻辑专名指称的对象，只能是这样的对象：无论在我想指涉它们的任何处境下，我都不会在关于它们的存在的问题上出错。物理对象和其他人类存在都不满足这个条件，因此不可能是逻辑专名的指称。唯一一种满足该条件并因此可以是逻辑专名指称的具体对象，是人自己，以及他自己的思想或转瞬即逝的感觉材料。通过这种推理，罗素开始相信，无论我们何时思考或谈论物理对象或他人，我们所使用的词都是在描述它们，而非直接命名它们。此外，我们所相信的命题，绝不包含物理对象或他人作为其组成部分，而总是完全由如下东西构成：作为我们所使用的描述性词项意义的性质和关系，加上作为逻辑语词意义的抽象概念，以及可以作为逻辑专名指称的、相对较少的具体的殊体。这是罗素1910年发表的文章《亲知知识和描述知识》中表达的核心原则之一。(13)
罗素用于决定包含摹状词句子的逻辑形式的规则
罗素理论的适用范围
至此我们只考虑了一小类句子——否定存在句。现在是时候将罗素的摹状词理论扩展到一类更广阔的情况。请考虑句子α is F，其中α或者是一个“这个”这样的指示词，一个“柏拉图”这样的日常专名，要么是一个这个G这样的单称限定摹状词。罗素承认，关于α和句子α is F的分析，有两种可能性。(14)
（i）α是一个逻辑专名，在这种情况下该句子的逻辑形式只是Fα。
（ii）α是一个限定摹状词或隐藏的限定摹状词，在这种情况下该句子的逻辑形式是∃x∀y ［（Gy↔y=x）&Fx］。(15)
为了确定在任一给定的情况下，究竟哪种可能性占上风，罗素使用了两项测试：
T1．在不知道α指涉何物的情况下，你是否可以理解α is F的意义？如果答案是肯定的，那么α就不是一个逻辑专名，而必须被分析为一个摹状词。
T2．即使α没有指称，α is F是否仍然是有意义的？如果答案是肯定的，那么α就不是一个逻辑专名，而必须被分析为一个摹状词。
罗素下述引自《数学原理》（Principia Mathematica）的段落清楚地陈述了第二项测试：
无论何时，只要一个命题的语法主语可以被设想为不存在，而又不使该命题变得无意义的话，这个语法主语就肯定不是一个［逻辑］专名……在所有这种情况下，命题必定可以被这样分析，以至于作为其语法主语的东西会消失。(16)
当罗素将这些测试用于包含这个如此这般的这种单称摹状词短语的句子，就像用于包含柏拉图这样的日常专名的句子时，他便得出如下结论：它们一定可以以一种与他的摹状词理论相一致的方式被分析。
歧义和排中律
对他分析的上述扩展，允许他去处理否定存在句问题——这是他的分析的原动力所在——之外很多附加的难题。其中一项难题涉及经典逻辑的法则，即排中律。罗素在《论指谓》中说了如下关于该难题的内容。
根据排中律，“A是B”或“A不是B”必定为真。因此，“当今的法国国王是秃子”或“当今的法国国王不是秃子”必定为真。但如果我们列举出秃顶的东西和不秃顶的东西，我们不会在任何一张列表中发现当今的法国国王。喜欢合题的黑格尔主义者们可能会得出结论说，他戴着假发。(17)
请考虑这些句子：
14a．当今的法国国王是秃子。
b．当今的法国国王不是秃子。
在这段话中，罗素似乎建议说，（14a）和（14b）都不为真。但这似乎违反了排中律——这条一般性的逻辑法则告诉我们，对任意一个句子S而言，S或～S为真。既然罗素认为这条法则有效，那么他就需要一种方法来化解这条明显的反例。
做到这一点的关键在于，他关于确定包含限定摹状词句子的逻辑形式的一般规则R。
R．Ψ［the Φ］⇒∃x∀y ［（Φy↔y=x）&Ψx］
这条将一个句子转变为其逻辑形式的规则说，如果一个限定摹状词与一个附加成分Ψ一同出现在某个句子中，那么它可以通过如下方式被消解（以此我们将被带得距离该句子的逻辑形式更近）：把该摹状词替换为一个变量，并引入量词加上以上提到的唯一性条款。
在句子（14a）的情况下，Ψ对应于短语是秃子，而摹状词是当今的法国国王。把这些代入R的左边半部分的形式中，我们得到了（14a’）。
14a’．B ［当今的法国国王］
将R用于给出逻辑形式（1fa）。
1fa．∃x∀y ［（Kyf↔y=x）& Bx］(18)
在给出规则R的时候，罗素自己就需要解释限定摹状词对任何包含它的句子所做的贡献。由此，R被意图用于所有句子，无论这些句子有多复杂。出于这种考虑，让我们将它用于稍微复杂一些的例子（14b）。
罗素首先会把该句子表达为一种更方便的形式。
14b’．～B ［当今的法国国王］
有两种方法使用R的方法，这取决于我们选择（b’）的哪个部分来充当Ψ的角色。如果我们认为（14b’）中的Ψ就是（14a’）中的，即谓词B，那么我们就把（14b’）视作（14b’1），并在括号内使用R。
14b’1．～（B ［当今的法国国王］）
这提供给我们
1fb1．～∃x∀y ［（Kyf↔y=x）& Bx］
另一方面，如果我们用（14b’）中的～B充当Ψ的角色，那么就会把（14b’）处理为（14b’2），而此时对R的使用会提供给我们（1fb2）。
14b’2．（～B ［当今的法国国王］）
1fb2．∃x∀y ［（Kyf↔y=x）& ～Bx］
因此，罗素关于将英语句子与其逻辑形式关联起来的原则R，便产生出这样的结论：包含摹状词的否定句是有歧义的。
（14b）的两种解释——（1fb1）和（1fb2）——之间的区别是什么呢？前者可以被改写为：情况不是这样的，即存在着这么一个人，他既是秃子，又是作为法国国王的唯一一人；后者则是：存在着这么一个人，他既不是秃子，又是作为法国国王的唯一一人。后者在逻辑上蕴涵：存在一个法国国王，但前者则不然。同样请注意，（1fa）与（14b）的两种逻辑形式都不相容——也就是说，（1fa）和（1fb1）不可能同时为真，而（1fa）和（1fb2）也不可能同时为真。然而，（1fa）和（1fb2）却可以同时为假；当不存在唯一一个法国国王时，二者都为假。这并不违反排中律，因为（1fb2）并非（1fa）在逻辑上的否定。相反，（1fb1）是（1fa）在逻辑上的否定；这二者不可能都不为真。如果其中一方为假，那么另一方必定为真，完全如排中律宣称的那样。
我们现在可以看到摹状词理论是如何解决罗素关于排中律的难题的。该法则适用于逻辑形式。当我们审视（14a）和（14b）的逻辑形式时，它们并没有提供针对该法则的反例。这与如下观察是相容的：有一种理解（14a）和（14b）的方式，在其中两者都不为真。这是因为（14b）是有歧义的。如果将（14b）解释为（14a）在逻辑上的否定，那么当（14a）为假时（14b）总是为真，这条法则也得以维持。如果将（14b）解释为那种（14a）和（14b）可以都为假的情况，那么（14b）就不是（14a）在逻辑上的否定，而我们就没有关于排中律的示例。该难题就这样得到了解决。
摹状词的域
我们关于否定和摹状词相互作用的例子，提供了一种解释罗素某些术语的简便方法。当句子（14b）被分析为（14b’1）并最终拥有逻辑形式（1fb1）时，摹状词当今的法国国王被说成是取了窄的域（take narrow scope），并且在这个句子或命题中次要出现（secondary occurrence）。当（14b）被分析为（14b’2）并最终拥有逻辑形式（1fb2）时，这个摹状词被说成是取了宽的域（take wide scope），并且在这个句子或命题中主要出现（primary occurrence）。
另一个同样的例子由（15）给出，它可以被简便地呈现为15’，其中“F”被用来表达是出名的这种性质。
15．约翰相信坐在那里的那个人是出名的。
15’．约翰相信F［坐在那里的那个人］。
如同在否定句的情况下那样，罗素的理论预言说，对该句子存在两种解释，它也因此是有歧义的。在一种解释下，摹状词坐在那里的那个人取了窄的域并以次要出现的形式出现。根据这种解释，R自身在从句之内被使用，并产生出如下这样的逻辑形式
1f1．约翰相信（∃x∀y［（坐在那里的（y）↔ y=x）& Fx］）
在这种解释下，（15）告诉我们，约翰相信只有一个人坐在那里，而无论那个人可能是谁，他都是出名的。根据这种解读，（15）可能为真，即使并没有人坐在那里；如果玛丽坐在那里，而约翰并不知道那是她或认为她是出名的，那么该句子也为真——这里所需要的只是，他相信某个名人或其他人独自坐在那儿。
根据（15）的另一种解释，摹状词坐在那里的那个人，在句子或命题中作为一个整体，对信念谓词取宽的域，并以主要出现的形式出现。根据这种解读，R被用于15＇＇，而下划线所标示的表达式则承担规则中Ψ的角色。
15＇＇．约翰相信F ［坐在那里的那个人］
这导致了如下逻辑形式：
1f2．∃x∀y［（坐在那里的（y）↔ y=x）&约翰相信Fx］
当（15）被解释成这样时，它告诉我们，有一个且只有一个人坐在那里，并且约翰相信那个人是出名的。为了使得这为真，确实正好必须有一个人坐在那里，而且约翰必须相信那个人是出名的；但是，如下事情却不是必然的：约翰有任何关于那个人在哪里的想法，或相信任何人坐在那里。
域、命题态度句以及关于乔治四世和《威弗利》作者的难题
罗素用摹状词理论去解答的另一个逻辑难题，涉及如下两种东西：作为命题态度归属句（包含相信、知道、断言、怀疑、期望等动词的句子，这种句子报告了一个施事者和一个命题之间的关系）而为人所知的那种构造，以及时常作为同一性替换（the substitutivity of identity）而被提到的逻辑法则。以下是罗素在《论指谓》中对该难题的陈述。
如果a与b等同，那么对其中一方而言为真的东西对另一方都必为真，而且任何一方都可以在任何命题中被替换为另一方，而不改变该命题的真假。现在，乔治四世希望知道司各特是否是《威弗利》的作者，而事实上司各特就是《威弗利》的作者。因此我们可以将《威弗利》的作者替换为司各特，并由此证明乔治四世希望知道司各特是否是司各特。但很难认为欧洲首屈一指的绅士会对同一律感兴趣。(19)
尽管远非一种清楚的模型——罗素在此前后不一致地来回摇摆于谈论表达式和谈论这些表达式标示的个体之间，就像摇摆于谈论句子和谈论这些句子表达的命题之间——但这段话所展现的问题已足够清楚。以下论证中的句子P1和P2看上去为真，即使相应的结论C看上去为假。
P1．乔治四世想知道司各特是否是《威弗利》的作者。
P2．司各特是《威弗利》的作者——司各特=《威弗利》的作者
C．乔治四世想知道司各特是否是司各特。
使得这种考察陷入麻烦的，显然是同一性替换律所制造的冲突，该法则可以被陈述如下：
SI．当α和β是单称指涉性表达式（singular referring expression），且句子α=β为真，那么α和β指涉同一事物，而且在任何为真的句子里，其中一方对另一方的替换都总会产生出一个真句子。
如果P1和P2为真，而C服从规则SI，那么C一定也为真。但问题是它似乎并不是这样。
在《论指谓》的稍后部分，罗素主张，他的摹状词理论可以解决这个问题。
关于乔治四世好奇心的难题，现在似乎有一种很简单的解决方法。命题“司各特是《威弗利》的作者”，……（当以一种非缩写的方式写出时）并不包含任何我们可以将之替换为“司各特”的成分“《威弗利》的作者”。这并不妨碍在语词上将“《威弗利》的作者”替换为“司各特”所导致的那种推理的正确性，只要“《威弗利》的作者”在我们所考虑的命题中，具有我所说的那种主要出现。(20)
这段话的第二个句子包含着关键的想法。既然“《威弗利》的作者”是一个单称限定摹状词，那么它在逻辑上就不会是一个单称指涉性表达式，且因此就不会出现在对规则SI的使用中。（在讨论这个例子时，罗素把司各特当作一个逻辑专名对待。）这条规则和所有逻辑规则一样，只适用于句子的逻辑形式。因此，为了评估上述论证，P1和P2必须被代替为各自的逻辑形式。
既然P1是一个包含限定摹状词的复合句，那么它是有歧义的——在一种解读方式下，该摹状词以主要出现的形式出现，在另一种解读下，则以次要出现的形式出现。因此，该论证有两种重构——每一种对应于对P1的一种解读。(21)
论证1：P1中摹状词的主要出现
P1p．∃x ∀y［（y写了《威弗利》↔ y=x）&乔治四世想知道是否是司各特=x］
有且只有一个写了《威弗利》的人，而且乔治四世想知道他是不是司各特。
P2． ∃x ∀y［（y写了《威弗利》↔ y=x）&司各特=x］
有且只有一个写了《威弗利》的人，而且他是司各特。
C．乔治四世想知道是否是司各特=司各特。
论证2：P1中摹状词的次要出现
P1s．乔治四世想知道是否是∃x∀y［（y写了《威弗利》↔ y=x）&司各特=x］
乔治四世想知道是不是（有且只有一个写了《威弗利》的人，而且他是司各特）
P2． ∃x∀y［（y写了《威弗利》↔ y=x）&司各特=x］
有且只有一个写了《威弗利》的人，而且他是司各特。
C．乔治四世想知道是否是司各特=司各特。
摹状词以次要出现形式出现于其中的那种解读，被罗素当作是最自然的解读。出于这种考虑，让我们来评估一下论证2。假设P1和P2为真。那么乔治想知道一个特定的为真的命题——被P2表达的命题——事实上是否为真。但是，既然P2不是一个简单的同一性陈述α=β，而且在P1s中不存在可以替换为“司各特”的单称指涉性表达式，那么我们不能使用规则SI来从P1s和P2得出C。到目前为止一切尚好。
重要的是，注意到这不是事情的全部。因为在引文最后一句话里罗素说到：“这并不妨碍在语词上将‘《威弗利》的作者’替换为‘司各特’所导致的那种推理的正确性，只要‘《威弗利》的作者’在我们所考虑的命题中具有我所说的那种主要出现。”他的观点是，当摹状词被解释成以主要出现的形式出现在P1中时，前提P1p和P2的真并不担保结论C的真。但根据摹状词理论，SI在论证1和论证2中都不适用。因此，人们不能通过注意到如下事情来解释两种论证的不同以及论证2的无效：摹状词理论不允许人们通过将“《威弗利》的作者”替换为“司各特”来运用SI。
为了理解究竟什么应当对这两种论证的不同负责，我们最好从验证这一点开始：论证1中从前提到结论的步骤是保留了真理性的。如果P1p为真，那么有且只有一个个体写作了《威弗利》，而且当“x”被当作关于那个个体的逻辑专名时，这个句子——（i）乔治四世想知道是否是司各特=x——为真。反过来，它恰恰在如下情况下为真：乔治四世想知道一个特定的命题——即被句子（ii）司各特=x表达的命题——是否为真，此时“x”仍然被当作那个写作了《威弗利》的独一无二的人的逻辑专名。如果P2为真，那么这个个体不是别人，就是司各特，在这种情况下“x”和“司各特”都是关于同一个人的逻辑专名。（请回忆一下，在讨论这个例子时，罗素将“司各特”当作一个逻辑专名来那样来对待。）既然它们都是逻辑专名，那么它们具有相同的所指，这一点保证了它们意指相同的事物，因此，在任何句子中将一方替换为另一方，都不会改变被这个句子表达的命题。由此我们得出结论，司各特=司各特与（ii）司各特=x表达了同样的命题p。既然我们已经证明，乔治四世想知道p是否为真，那么C就也是真的。因此，在论证1中，从P1p和P2到C的推理，就得到了保留真理性的担保。
接下来请考虑论证2。如果P1s为真，那么乔治四世想知道一个特定的命题q是否为真——其中q是这样的命题：有一个个人写作了《威弗利》，而且这个人是司各特。如果P2为真，那么事实上q就为真。但是，这没有告诉我们任何关于乔治四世想知道命题p——司各特是司各特——是否为真的事情。既然人们显然可以想知道q是否为真，而不想知道p是否为真，那么论证2的前提就可以为真，而与此同时其结论则为假。因此该论证无效。
罗素的认识论与摹状词理论间的冲突
到目前为止，这个故事的寓意是：罗素的摹状词理论确实可以解释，在一种对前提P1的自然解释下，关于乔治四世的论证为何变得无效了；作为奖励，他还提供了关于如下问题的进一步解释：如果前提1以一种不同的方式被理解，那么上述论证就是有效的。但是，关于该理论在其他方面的成功使用，却仍然有问题。罗素看上去显然会认为，假定任何人会怀疑司各特是司各特这个命题是否为真，这是很荒谬的。(22)因此，当P1被分析为P1p，而“《威弗利》的作者”以主要出现的形式出现时，他除了认为P1为假外别无选择。然而，这是反直觉的，因为这个句子那个写作了《威弗利》的个体，就是乔治四世想知道其是否是司各特的那个人似乎很容易为真。从《论指谓》中摘取的如下段落说明，罗素自己似乎也会同意这一点。
当我说“乔治四世希望知道司各特是否是《威弗利》的作者”时，我一般的意思是“乔治四世希望知道是否有且只有一个人写了《威弗利》，而且司各特就是那个人”，但我们的意思也可能是：“一个人且只有一个人写了《威弗利》，而且乔治四世希望知道司各特是否就是那个人”。在后一种情况下，“《威弗利》的作者”以主要出现的形式出现；而在前一种情况下则是次要出现。后一种情况可以表达为“关于那个事实上写了《威弗利》的人，乔治四世希望知道他是否是司各特”。这可以是真的，例如，如果乔治四世曾在远处看到过司各特，并问道“那是司各特吗？”(23)
这是令人迷惑的。如果乔治四世不想知道司各特是司各特，那么在将P1解释为“《威弗利》的作者”以主要出现的形式出现于其中的情况下，P1如何可以为真？一种自然的回答是，为了在他所描述的那种情形下使这个句子为真，罗素无疑可以将日常专名“司各特”解释为一个隐藏的摹状词（在该句子中以次要出现的形式出现），而非一个逻辑专名。尽管罗素在《论指谓》中并没有强调这种日常名称的地位，但在后来的著作中他明确地坚称，这些名称可以用这种方式被理解。毫无疑问，这种观点可以在上述段落中起作用。
不过，还是有一些重要的问题。第一，这种观点——日常专名可以与摹状词（说话者将日常专名与摹状词结合在一起）意指相同的东西——尽管在罗素的先驱性工作之后又兴盛了几十年，但最终由克里普克在《命名与必然性》(24)中表明是有严重问题的。我们会在第二卷详细考察对专名的描述性分析；而现在，注意如下这些就够了：对P1如何可以在罗素描述的那种情形下——此时“《威弗利》的作者”被当作以主要出现的形式出现——为真的解释，其所依赖的脆弱基础，正是上述那种观点。(25)第二个问题，涉及罗素对在命题态度归属句中取宽域的摹状词的表述，这个问题避开了关于日常专名分析的争论。例如，请考虑（16）。
16．玛丽想知道《威弗利》的作者是否写了《威弗利》。
对这个句子最自然解释是，摹状词以主要出现的形式出现——一个人且只有一个人写了《威弗利》，而玛丽想知道是否是那个人写了《威弗利》。一个坚定地说出（16）的说话者——他意图的正是这种解释——可能清楚地知道谁是《威弗利》的作者，且偶然听到(26)玛丽说“他写了《威弗利》吗？”，并指向所谈论的那个人。似乎很清楚的是，如果（16）以这种方式被使用，那么它就表达了一条真理。
尽管罗素的摹状词理论似乎完美地捕捉到了这个事实，但在此情况下对该理论的自然运用，却与上一节中谈及逻辑专名的重要的认识论原则相抵触。如先前提到的那样，在他1910年发表的文章《亲知知识和描述知识》中，罗素的立场是，能作为逻辑专名指称的对象，只能是这样的对象：关于它们的存在，人们不可能出错。因为物理对象和他人不符合这个条件，所以他坚称，它们不可能是逻辑专名的指称。他似乎没有认识到的是，关于像（16）这样的例子的解释16p，这便产生出一种问题，在其中摹状词取宽的域。
16p．∃x ∀y ［（y写了《威弗利》↔ y=x）&玛丽想知道x是否写了《威弗利》］
如我们所见的那样，在罗素的论述中，它为真，当且仅当：一个人写了《威弗利》，并且在“x”被处理为一个关于那个人的逻辑专名时，句子玛丽想知道x是否写了《威弗利》为真。(27)如果我们现在被告知，不存在关于其他人的逻辑专名，那么这种表述就不够了。
事实上，问题还要更糟。罗素关于逻辑专名可能的指称的严格认识论原则，与一种关于如下命题的同样严格的原则联结在了一起：一个施事者可以考虑、相信、怀疑、断言等等。如罗素所说的那样：
分析包含摹状词命题的基本认识论原则是这样的：任何我们可以理解的命题，都必定完全由我们所亲知的成分构成。(28)
在罗素看来，既然人们可以亲知的事物只有人自身以及自己瞬间的思想和感觉，加上抽象性质和关系（即共相），那么人们不可能相信或考虑任何包含其他施事者或其他具体对象作为其成分的命题。我们只能在如下意义上相信或考虑一个包含这种对象o的命题，即通过相信或考虑这样一个命题，它陈述说某个（独一无二的）对象具有某些性质，而这些性质是o事实上具有的。在罗素的术语中，知道某个命题具有与o的这种关系，就是通过描述知道o。《亲知知识和描述知识》的一条核心原则就是，我们关于其他人和其他对象的所有知识，都是通过描述而得到的知识。罗素这样概括自己的观点：
这样来概括我们的整个讨论：我们开始于对两种关于对象的知识的区分，即亲知知识和描述知识。其中只有前者将对象自身带到我们的心灵之前。我们对感觉材料、很多共相甚或我们自身有亲知，但对物理对象或他人之心则没有。当我们知道正是这个对象具有我们所亲知到的某个或某些性质时，我们就拥有了关于它的描述知识；也就是说，当我们知道谈及的这个或这些性质只属于一个对象且不属于别的对象时，我们就被说成是通过描述而知道了关于那个对象的知识，无论我们是否亲知了这个对象。我们关于物理对象和他人之心的知识只是描述知识，这些描述经常像感觉材料那样被谈及。所有对我们来说可理解的命题，无论它们从根本上说是否是关于那些我们只能通过描述知道的事物的，都完全由我们所亲知的成分组成，因为一个我们不亲知的成分对我们而言是不可理解的。(29)
因此，罗素开始相信，无论我们何时想到或谈论物理对象或他人，我们所使用的语词都是在描述他们，而非直接命名他们。此外，我们相信或考虑的名词绝不包含物理对象或他人作为自己的成分，而总是完全由如下东西构成：作为我们所使用的描述性词项意义的性质和关系，加上作为逻辑语词意义的抽象概念，以及可以作为真正的逻辑专名指称的相对较少的具体的殊体。无论这条原则里可能有其他什么正确的东西，在将罗素的摹状词理论用于命题态度归属句（17a）和（17b）时，都具有灾难性后果（这从未被罗素直截了当地处理过）；在这些句子中，v是一个像相信、怀疑、断言或想知道这样的动词，它们将施事者与一个命题联系起来，而且补语从句S包含这样一个摹状词这个D，它可以被解释成在这个句子里作为一个整体以主要出现的方式出现。
17a．Av’s S（那个D）
b．Av’s是否是S（那个D）
当这些句子以上述方式被解释时，罗素的摹状词理论告诉我们，（17a）为真当且仅当（17ap）为真，而（17b）为真当且仅当（17bp）为真。
17ap．∃x ∀y ［（Dy↔y=x）&Av’s S（那个D）］
17bp．∃x ∀y ［（Dy↔y=x）&Av’s是否是S（那个D）］
反过来，只有当施事者与被S（x）表达的命题，具有那种被v表达的关系（相信、怀疑、断言或想-知道-某某的-真）时，（17ap）和（17bp）才为真，此时“x”被当作关于一个且只关于那个对象的逻辑专名，该对象具有被D表达的性质。《亲知知识和描述知识》的核心认识论原则是，当谈及的对象是一个物理对象或另一个人类时，施事者与该命题不可能具有任何认知关系。因此，这条原则具有如下结果：所有具有（17ap）和（17bp）这种形式的、涉及上述那种对象的例子，都为假。这样一来，罗素在《亲知知识和描述知识》中的主要认识论原则，便威胁到他摹状词理论一项最令人印象深刻的运用，包括他在《论指谓》中对关键性的、具有激发性的例子——乔治四世对司各特和《威弗利》作者的好奇心——的著名处理。尽管这种冲突暗示，罗素的总体观点显然有某种错误，但他从未解决这个问题，或以一种系统的方式处理它。
语言分析和形而上学实践
不过，当与摩尔的如下坚持相结合的时候，对语言的罗素主义逻辑分析就是一种巨大的成功：常识，是在哲学中创造一种被证明是具有令人印象深刻效力的哲学分析风格的起点。这可以通过如下方式来加以阐明：将它用于摩尔和罗素的绝对唯心论先驱们的一条原则。如我在本章开始处提到的那样，这些哲学家坚称，所有实在都是精神性的，而且实在的全体是一个单一且统一的对象——要么是一个神性的心灵，要么（根据唯心论者）是一个由相互依赖的诸多心灵构成的整体系统。如后来提到的那样，导致了该图景的一条想法，是一种扩张性版本的内在关系的实在性原则。简言之，这种版本的原则认为，每个对象的本质和存在都依赖于任何其他对象，这样一来，只要任何实体缺失了哪怕它实际所具有的任何一个性质，那么无论宇宙自身还是其中的任何一个部分，就都不会存在了。
这种令人印象深刻的反直觉主张，是两种更基本的想法的产物。一是，在任何一个对象的性质之中，有着与其他对象有关系的性质，而这些性质又继续具有这种性质。例如，我具有居住在哈里森大街和普林斯顿之间这种性质。因此，你就具有这种属性：阅读了某个居住在哈里森大街和普林斯顿之间的人所写的东西。显然，这种例子可以无限叠加下去。我们可以如此来概括这种观点：对任何一个对象o和o所具有的性质P而言，都存在一些关系性质PS——在具有P这一点上与o相似——和PD——在不具有P这一点上与o不同。既然o本身具有P，那么所有其他具有P的对象都具有PS，而不具有P的则具有PD。除此之外，如果o开始不再具有P，那么所有现在具有PS的对象就会不再具有PS，而所有现在具有PD的对象就不会再具有PD。因此，一个对象中发生的任何在性质上的改变，都涉及所有对象性质上的改变。(30)
如果考虑到该论证中所使用的关于一个对象的性质的广义的概念，即任何可以真正谓述给这个对象的东西，那么上述结论自身并没多大意思。但是，当与绝对唯心论者通常坚持的第二条原则结合在一起时，它就不无吸引人之处了。这第二条原则是，一个对象的每种属性，在如下这种意义上对它来说都是本质上的——如果没有该属性，那么这个对象就不会存在。这条疯长的本质论原则，加上这种观察——每个对象的性质都与其他所有对象的性质内在相关——共同导致了内在关系的实在性原则的扩张版本，这种版本受到很多绝对唯心论者的青睐。
摩尔在1919年发表了对这种观点的咄咄逼人的攻击，使之服从于一种精心的分析，并论证说它建基于概念混淆。(31)尽管我们无需追随他迂回曲折的缜密讨论，但可以用罗素关于逻辑形式和语法形式的区分来阐明摩尔的基本观点。有鉴于此，请考虑下述关于疯长的本质论的通用论证。
S1．这是必然的：如果a=b，那么a的任何属性是b的一种属性。
S2．因此，如果a具有性质P，那么这是必然的：如果b不具有P，那么b≠a。
S3．更一般地说，如果a具有P，那么任何不具有P的东西必然不是a。
S4．所以，如果a具有P，那么这必然为真：任何不具有P的东西都不是a。
S5．如果任何不具有P的东西都不是a必然为真，那么对世界的任何可能状态w（也就是说，对任何一种世界可能是的方式w）和无论任何对象o来说，如果o不具有P且世界处于状态w中，那么o就不会是a。
S6．既然a总会是a，无论世界可能处于何种可能状态（假设a在世界可能所处的那种状态中继续存在），都不存在这样一种可能的状态w：在世界处于w中时，a会在不具有P的状态下继续存在。
S7．既然世界不可能是这样的，即在那种可能的方式中a会在不具有P的状态下继续存在，那么a不会在不具有P的状态下继续存在。
S8．既然同样的论证适用于任何对象的任何性质，那么一个对象的每个性质在这种意义上都是该对象的本质属性——在不具有那种性质的情况下该对象不会继续存在。
这种论证的第一条前提显然为真，而每个步骤都散发着似乎合理的气息；但其结论却是令人难以置信的。怎么会这样呢？我们如下的常识信念如此地令人迷惑和不可靠，而就被这样一个小小的论证驳倒了吗：我们自身和周围的事物，可以具有至少一点点不同的历史？当然不是。混淆之处在于这个论证本身，而且这可以被逻辑分析揭示。
如上所述，S1以及从S4到S8的过程都是好的。问题在于，某些包含了语词这是必然的的句子是模棱两可的，这些句子影响了到步骤S2、S3、S4的推理。这种论证可以按照如下方式理解：所有该语词的出现，都表达了必然为真这个性质。因此，S1可以被理解为具有LS1这种逻辑形式：
LS1．这是必然为真的：［如果a=b，那么a的每个性质都是b的一个性质］
在此，必然为真这个性质被归属于被括号中的句子所表达的命题——即这样一个命题：如果a与b相等同，那么a的每个性质都是b的一个性质。相比之下，S2是有歧义的，因为必然性算子可以取不同可能的域。在此我们有一个英语中无处不在的、有歧义的域的例子；一些包含摹状词的句子，由于摹状词可以取不同的域，因而是有歧义的；同样，由于必然性算子的不同可能的域，一些句子也是有歧义的。
根据一种解释，S2的逻辑形式是LS2a，而根据另一种解释则是LS2b。
LS2a．这是必然为真的：［如果a具有性质P，那么（如果b不具有性质P，那么b≠a）］
LS2b．如果a具有性质P，那么这是必然为真的：［如果b不具有性质P，那么b≠a］
LS2a得自LS1。由于LS2a括号中的句子是LS1括号中的句子的一个逻辑后承，因此如果其中一方表达了一条必然真理，那么另一方一定也是如此。但是，LS2b在逻辑上并不得自LS1。LS1告诉我们，不可能有这样一种可能状态w，即如果世界处于w之中，则a会是与b完全相同的对象，而并不具有与b相同的性质。LS2则告诉我们某些完全不同的东西：如果世界实际上处于这样一种状态——a具有一种特定的性质P——之中，那么不可能有这样一种状态——如果世界处于这种状态中，那么一个不具有P的对象b会是与a相同的对象。为了在LS1的基础上得出这个结论，人们会需要加上一条进一步的假设，即如果世界实际上处于a具有P的状态中，那么不可能存在这样的状态w——如果世界处于w中，则a会不具有P。但是，既然上述论证旨在证明这一点，那么将它作为一条假设引入，就会使该论证变为循环论证。因此，如果上述论证有任何机会达到自己的目的，那么S2必须被解释为具有逻辑形式LS2a。
同样的推理证明，如果S3得自LS2a，那么它必须具有逻辑形式LS3a。
LS3a．这是必然为真的：［对任何一个对象o而言，如果a具有性质P，那么（如果o不具有性质P，则o≠a）］
然而，现在没有方法得到S4，S4的逻辑形式是LS4，是有歧义的。
LS4．如果a具有P，那么这是必然为真的：［对任何一个对象o而言，如果o不具有性质P，则o≠a］
和之前一样，无法有效地从LS3a中推导出LS4，因为缺少那种需要被证明的假定。当然，既然S3是有歧义的，那么它就有另一种解释，在这种解释中S4确实得自S3，而S3在这种解释中具有与S4相同的逻辑形式。但是，根据那种解释，S3并不得自LS2a。
总而言之，对疯长的本质论的逻辑分析揭示出，这种本质论依赖于一种隐藏的歧义性。论证中某些特定的关键句子，具有不止一种逻辑形式。这种事实——每个步骤都有这样一种解释，根据该解释，这个步骤都在逻辑上非循环地得自之前的诸步骤——为该论证营造了似乎合理的气氛。但是，不存在一种一致的方式来解释那些有歧义的句子，以使得每个步骤都在逻辑上非循环地得自之前的诸步骤。由于这一点，该论证丝毫没有驳回这种日常信念：我们自身和周围的事物可以具有至少一点点不同的历史。简言之，唯心论者丝毫没有驳回支持该信念的合理假设，也丝毫没有确立他们宏大的形而上学主题。对我们来说，这种结果非常有用地阐明了，在哲学论证中产生自摩尔和罗素早期著作的、关于分析的设想的力量。
(1) 第一篇文章首先发表于Mind 12（1903）；第二篇则首先发表于Proceedings of the Aristotelian Society，1919—1920；两篇文章都在摩尔所著Philosophical Studies（Totowa, NJ: Littlefield and Adams, 1968）一书中收录。
(2) 译者注：希腊神话中长有翅膀的马。
(3) Bertrand Russell, The Principles of Mathematics（New York: Norton and Co.）.
(4) Ibid., p. 43.
(5) The Principles of Mathematics., p. 449.
(6) 译者注：出自1954年美国的杰克·阿诺德导演的同名电影。
(7) The Priciples of Mathematics., p. 449.
(8) Russell，“On Denoting，”Mind 14（1905）；reprinted in Logic and Knowledge，R. C. Marsh，ed.（New York：Capricorn Books, 1956），p. 45。所有引文均出自Marsh的文本。
(9) Bertrand Russell, Introduction to Mathematical Philosophy（New York: Dover, 1993）, pp. 169—170. （First published by Allen and Unwin, London, and Macmillan, New York, 1919.）
(10) 在此（以及在“对这种语言的罗素主义解释”中）给出的关于命题——这些命题被存在概括和全称概括所表达——的真值条件，比罗素本人所给出的更详尽，尽管罗素主义者在精神上也给出了这些真值条件。他们对这些想法的使用，首先由阿尔弗雷德·塔尔斯基在二十世纪三十年代所发展。一种对上述模式的变体，将SOME和ALL当作从命题函项到真值的函项，而将NEG、CONJ等当作从真值到真值的函项。这种转变的一项好处是，把被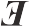
x Fx表达的命题同被将F-性赋予对象的命题函项有时为真表达的命题区别开来。
(11) 如果我告诉自己的学生那个在家庭作业中得了A的同学无需参加考试，那么他们自然会假定只有一位同学在这项作业上得了A（以及将会有一门考试）。
(12) 译者注：“y is so and so”意为“y是如此这般的”。
(13) 参阅Russel，“Knowledge by Acquaintance and Knowledge by Descri ption，” Proceedings of the Aristotelian Society 11（1910—1911），reprinted in Propositions and Attitudes，N. Salmonand S. Soames，eds.（Oxford：Oxford University Press, 1988）。
(14) 我在此只用最简单的句子——由一个主语和一个动词组成——举例说明。罗素会将其扩展到更广阔的范围，包括具有各种不同语法形式的简单句，比如含有及物动词的句子——α v’s β。但是，我们会排除一些特例，比如希腊人崇拜宙斯和科学家寻求对癌症的治愈。
(15) 译者注：原著中使用的“&”符号有两种写法，为方便起见，翻译时统一译为“&”，以下不再一一赘述。
(16) Russell and Alfred North Whitehead，Principia Mathematica（Cambridge：Cambridge University Press，1950），vol. 1，chapter 3，p. 66.
(17) Russell，“On Denoting，”p. 48.
(18) 在此“B”是谓词是秃子的缩写，“K”是二元谓词是……的国王的缩写，而“f”则命名法国。
(19) “On Denoting,” pp. 47—48 in Marsh.
(20) “On Denoting” pp. 51—52.
(21) 在讨论此论证时，我忽略了时态。
(22) 关于当代对罗素主义那种允许上述怀疑的修订，请参阅NathanSalmon，Frege’s Puzzle（Cambridge MA：MIT Press, 1986）；Scott Soames，Beyond Rigidity（New York：Oxford University Press, 2002）；以及下面这本书的导论：Salmon and Scott Soames，eds.，Propositions and Attitudes（Oxford：Oxford University Press, 1988）。
(23) “On Denoting，”p. 52，着重号为本书作者所加。
(24) Saul Kripke，Naming and Necessity（Cambridge，MA：Harvard University Press, 1980）；originally published in Semantics of Natural Languages，D. Davidson and G. Harman，eds. （Dordrecht：Reidel, 1972），pp. 253—355。引文出自1980年版。
(25) 请参阅萨蒙（Salmon）和索姆斯对此所做的当代的罗素主义解释。
(26) 译者注：原书中误为“overhead”，应为“overheard”。
(27) 将一个变量处理为关于一个对象o的逻辑专名，这可以有两种理解方式：要么是，把该变量替换为一个新的关于o的逻辑专名（通过在变量下增加下划线来获得）；要么是，求出如下式子的值：相对于将o赋值给该变量而言，该变量在式子中有一种自由出现。
(28) “Knowledge by Acquaintance and Knowledge by Description,” p. 23 in Propositions and Attitudes.
(29) Knowledge by Acquaintance and Knowledge by Description.，p. 31.
(30) 该论证取自J.M.E. McTaggart，The Nature of Existence，vol. 1（Cambridge：Cambridge University Press, 1921）。
(31) “External and Internal Relations,” Proceedings of the Aristotelian Society, 1919—1920, reprinted in G. E. Moore, Philosophical Studies（Totowa, NJ: Littlefield and Adams, 1968）.