-
1.1第一章 天体的运行
-
1.1.1第一节 我们的星辰系统
-
1.1.2第二节 天界现象
-
1.1.3第三节 时间和经度的关系
-
1.1.4第四节 如何确定天体的位置
-
1.1.5第五节 地球的周年运动及其结果
-
1.2第二章 望远镜
-
1.2.1第一节 折射望远镜
-
1.2.2第二节 反射望远镜
-
1.2.3第三节 折反射望远镜
-
1.2.4第四节 望远镜摄影术
-
1.2.5第五节 大型光学望远镜
-
1.2.6第六节 射电望远镜
-
1.2.7第七节 太空望远镜
-
1.3第三章 太阳、地球、月球
-
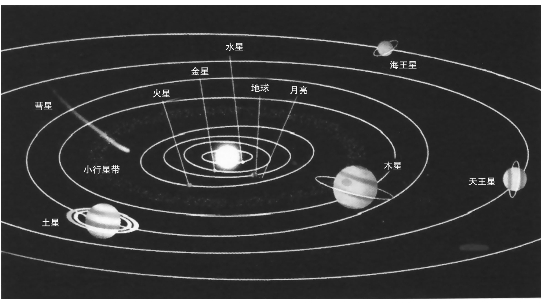
1.3.1第一节 太阳系的结构
-
1.3.2第二节 太阳
-
1.3.3第三节 地球
-
1.3.4第四节 月球
-
1.3.5第五节 月食
-
1.3.6第六节 日食
-
1.4第四章 行星及其卫星
-
1.4.1第一节 行星的轨道
-
1.4.2第二节 水星
-
1.4.3第三节 金星
-
1.4.4第四节 火星
-
1.4.5第五节 小行星群
-
1.4.6第六节 木星及其卫星
-
1.4.7第七节 土星及其卫星
-
1.4.8第八节 天王星及其卫星
-
1.4.9第九节 海王星及其卫星
-
1.4.10第十节 以前的大行星冥王星
-
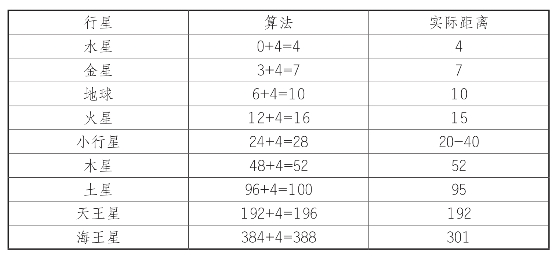
1.4.11第十一节 太阳系的比例尺
-
1.4.12第十二节 引力和行星的称量
-
1.5第五章 彗星和流星
-
1.5.1第一节 彗星
-
1.5.2第二节 流星
-
1.6第六章 恒星
-
1.6.1第一节 星座
-
1.6.2第二节 恒星的本质
-
1.6.3第三节 恒星的距离
-
1.6.4第四节 恒星系统
-
1.6.5第五节 星云
-
1.7第七章 星系和宇宙
-
1.7.1第一节 银河系
-
1.7.2第二节 河外星系
-
1.7.3第三节 膨胀的宇宙
-
1.7.4第四节 大爆炸宇宙学
-
1.7.5第五节 微波背景辐射
-
1.7.6第六节 宇宙的组成
-
1.7.7第七节 宇宙的结构
-
1.7.8第八节 宇宙的演化
-
1.8第八章 探索地外生命
-
1.8.1第一节 不明飞行物——UFO
-
1.8.2第二节 地球生命之源
-
1.8.3第三节 探索太阳系
-
1.8.4第四节 探索银河系
1
通俗天文学