1.2 计算机进制与信息编码
1.2.1 进位计数制
1.进位计数制的概念
在人类历史发展的过程中,根据生产、生活交流的需要,人们创立了数。 数制就是用一定的符号和规则来表示数的方法。
进位计数制是指用一组特定的数字符号按照先后顺序排列起来,从低位向高位进位计数表示数的方法,简称进制。 例如,十进制数2615就是用2、6、1、5这4个数码从低位到高位排列起来的,表示二千六百一十五。 在进位计数制中包含两个基本要素:“基数”和“位权”。
(1)基数:一种进位计数制中允许使用的基本数字符号的个数称为基数。 这些数字称为数码或数符。
(2)位权:就是单位数码在该数位上所表示的数量。 位权是以指数形式表达,指数的底是计数进位制的基数。 例如,在十进制数327.5中,3表示的是300(3×102),2表示的是20(2×101),7表示的是7(7×100),5表示的是0.5(5×10-1)。
任何一个数都可以按位权展开式表示,位权展开式又称为乘权求和。
一般地,任何一个n位R进制数都是可以用数字乘权求和的形式来表达的,其公式为
(K1K2…Kn)R=K1×Rn-1+K2×Rn-2+…+Kn×R0
其中,R为基数,可以是2、8、10、16等。
另外,在运算中还应遵守“逢R进1,退1当R”的进位规则。
2.常用的进位计数制介绍
常用的进位计数制有二进制、八进制、十进制和十六进制。
(1)二进制。
二进制有两个数码:0和1。
进位规则是“逢二进1,退1当二”。 因此运算规则如下。
二进制加法规则:0+0=0 0+1=1 1+0=1 1+1=10
二进制减法规则:0-0=0 1-0=1 1-1=0 10-1=1
二进制乘法规则:0×0=0 0×1=0 1×0=0 1×1=1
(2)八进制。
八进制有8个数码:0、1、2、3、4、5、6、7。
进位规则是“逢八进1,退1当八”。
(3)十六进制。
十六进制有16个数码:0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F。
进位规则是“逢十六进1,退1当十六”。
(4)十进制。
日常生活中最常用的是十进制。
十进制,它有十个数码:0、1、2、3、4、5、6、7、8、9。
进位规则是“逢十进1,退1当十”。
二进制、八进制、十进制和十六进制这4种进制之间的对应关系如表1-1所示。
表1-1 4种进制之间的对应关系
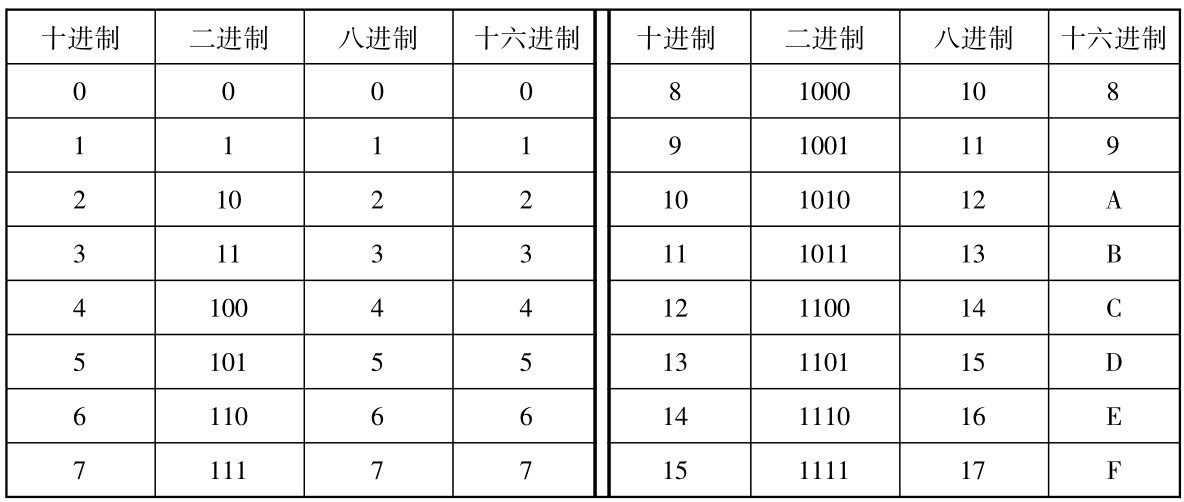
为了避免以上不同进位数制的数在使用时产生混淆,在给出一个数时,应指明它的数制,通常用字母D、B、O、H或用下标10、2、8、16分别表示十进制、二进制、八进制和十六进制数。 其中,十进制可以不做标明。
例如:1124D、11011B、374O、4FE2H
或(1124)10、(11011)2、(374)8、(4FE2)16
1.2.2 数制之间的相互转换
1.R进制数转换为十进制数
方法特别简单,先将R进制数按位权展开式展开,然后按十进制规则进行计算,其计算结果就是转换后的十进制数。
例:将(325)8、(1010011)2转换为十进制数。
(325)8=3×82+2×81+5×80=192+16+5=213
(1010011)2=1×26+0×25+1×24+0×23+0×22+1×21+1×20=64+16+2+1=83
2.十进制数转换为R进制数
这里的R通常是表示二、八、十六。 转换规则分成整数部分和小数部分:
整数部分:采用“除以R取余法”。 即用十进制数反复地除以R,记下每次所得的余数,直至商为0。 将所得余数按最后一个余数到第一个余数的顺序依次排列起来即为转换结果。
例:将十进制数(124)10转换成二进制数,转换过程如下:
所以(124)10=(1111100)2。
小数部分:采用“乘以R取整法”。 即用十进制小数乘以R,得到一个乘积,将乘积的整数部分取出来,将乘积的小数部分再乘以R,重复以上过程,直至乘积的小数部分为0或满足转换精度要求为止,最后将每次取得的整数依次从左到右排列即为转换结果。若要转换成二进制小数,则采用“乘2取整法”。
例:将十进制数(0.625)10转换成二进制数,转换过程如下:
小数部分为0.000,转换结束。
所以(0.625)10=(0.101)2。 在本例中,能够精确转换,没有丝毫误差。 特别要注意的是,并非所有的十进制小数都能完全准确地转换成对应的二进制小数,(0.1)10就是一个例子,有兴趣的读者不妨试一试,看看转换过程中会出现什么情况。
对于既有整数部分又有小数部分的十进制数,转换成R进制数,转换规则是:将该十进制数的整数部分和小数部分分别进行转换,然后将两个转换结果拼接起来即可。
例:将十进制数(124.625)10转换成二进制数,转换过程如下:
因为,(124)10=(1111100)2
(0.625)10=(0.101)2
所以,(124.625)10=(1111100.101)2。
以上介绍了十进制数与R进制数(在此主要是指二进制、八进制及十六进制数)的相互转换方法,为便于记忆,可简单归纳为:R至十,位权展开式求和;十至R,用整部除R取余,小数乘R取整,并特别注意转换结果的排列规则(除R取余法是“先余为低,后余为高”;乘R取整法是“先整为高,后整为低”)。
3.二进制数与八进制、十六进制数之间的特殊转换
由于二进制数与八进制、十六进制数的特殊关系(8和16都是2的整数次幂:8=23,16=24),所以由二进制转换成八进制、十六进制,或者做反向的转换,都非常简单。
(1)二进制数与八进制数的相互转换
把一个二进制整数转换成八进制数的方法是,从二进制数的小数点开始从右向左,将每3位数字分成一组(最后一组若不足3位,可不补“0”),把每组数换成对应的八进制数码即得到转换结果。
例:将二进制整数10101111001转换成八进制数,转换过程如下:
分组: 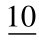
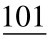
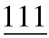
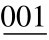 (整数分组,不足3位,可不补0)
(整数分组,不足3位,可不补0)
对应值: 2 5 7 1 (每组对应一位八进制数)
所以,(10101111001)2=(2571)8。
把二进制小数转换成八进制数的方法与整数转换相同,只是应注意以下两点:
①分组方向是小数点开始从左向右;
②分组时末尾若不足3位,必须在右边补0,补足3位,否则会出错,读者应特别注意。
例:把二进制数11100101.1101转换成八进制数,转换过程如下:
所以(11100101.1101)2=(345.64)8。
本例中,小数部分分组时,最末一组只有一位,应补两个0,成为“100”,若不补0,将得到错误结果:(11100101.1101)2=(345.61)8。
八进制数转换成二进制数的方法与上述转换过程相反,转换时,将每一位八进制数展开为对应的3位二进制数字串,然后把这些数字串依次拼接起来即得到转换结果。
例:把八进制数532.07转换成二进制数,转换过程如下:
所以,(532.07)8=(101011010.000111)2。
再看一个例子,把八进制21.34转换成二进制数,转换过程如下:
将转换结果中的前导0及小数部分尾部的0去掉,所以,(21.34)8=(10001. 0111)2。
(2)二进制数与十六进制数的相互转换
二进制数与十六进制数的相互转换方法和上述二进制与八进制间的转换相同,只是在转换时,用4位二进制数与1位十六进制数互换,具体过程不再赘述,下面给出一些转换实例。
例:(1101 0101 1011)2=(D5B)16
(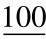
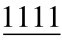 .
.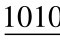 )2=(4F.A)16
)2=(4F.A)16
(ABC)16=(1010 1011 1100)2
(E64.5A)16=(111001100100.01011010)2
(3)八进制数与十六进制数的相互转换
这两种数制的相互转换可借助二进制或十进制作为桥梁来进行。
例:(576)8=(101111110)2=(17E)16
(2FB)16=(763)10=(1373)8
注意:每1位八进制数可用3位二进制数表示,每位十六进制数可用4位二进制数表示,这是以上3种数制相互转换的要点,并且必须记住表1-1中所列的基本对应关系。
1.2.3 计算机中的数据单位
计算机内所有的信息(无论是程序还是数据)都以二进制数的形式存放。 一位二进制数是数据的最小单位,称为位(bit)。 计算机在处理信息时,一般以一组二进制数作为一个整体,这组二进制数称为一个字(word)。 一个字的二进制位数称为字长。 不同计算机系统内部的字长不同。 计算机中常用的字长有8位、16位、32位、64位等。 字长是衡量计算机性能的一个重要指标。
一般用字节(Byte)作为基本单位来度量计算机存储容量。 一个字节由8位二进制数组成。 在计算机内部,一个字节可以表示一个数据,也可以表示一个英文字母或其他特殊字符;一个或几个字节还可以表示一条指令;两个字节可以表示一个汉字等。
有关存储的常用度量单位及其换算关系如下:
1KB=210Byte=1024B(Byte)
1MB=220Byte=1024KB=1024×1024(Byte)
1GB=230Byte=1024MB=1024×1024×1024(Byte)
1TB=240Byte=1024GB=1024×1024×1024×1024(Byte)
其中,K、M、G、T分别称为千、兆、吉、太。
为了便于对计算机内的数据进行有效的管理和存取,需要对内存单元进行编号,即给每个存储单元一个地址。 每个存储单元存放一个字节的数据。 如果需要对某一个存储单元进行存储,必须先知道该单元的地址,然后才能对该单元进行信息的存取。 应当注意,存储单元的地址和存储单元的内容是不同的。
1.2.4 数据编码
1.数据与信息的概念
数据(Data)是指计算机能够接收和处理的物理符号,包括字符(Character)、表格(Table)、声音(Sound)、图形(Picture)和影像(Video)等。 数据可以在物理介质上记录和传输。
信息本身也是数据,但数据不一定是信息。
单独的数据通常不能表示完整的意义,经过解释并赋予一定的意义后便成为信息,因此信息是人们消化了的数据,是数据的具体含义。 数据与信息既有联系又有区别。数据是信息的载体,信息则是数据的具体内涵。 对同一数据可能有不同的解释,使之成为内容不完全相同的信息,如36可以是年龄36岁,也可以是鞋长36码。 对同一信息也可能由不同的数据来表示,例如,同样一条新闻,在不同的报纸上发布,文字内容可能不同。
2.计算机中的字符信息编码
在计算机处理的数据中,除了数值型数据外,非数值型数据(如字符、图形)也占很大比重。 其中,字符是日常生活中使用最频繁的非数值型数据,它包括了英文字母、数字、符号及汉字等。 由于计算机只能识别二进制代码,为了能够对字符进行识别和处理,同样要对字符进行二进制编码表示。 每一个英文字符和一个确定的编码相对应,而一个汉字字符和一组确定编码相对应。
计算机中英文字符主要用ASCII编码,简体中文字符主要用变形的国标码。
(1)ASCII码。 ASCII码是“美国信息交换标准代码”(American Standard Code for Information Interchange)的简称,该标准已经被国际标准化组织(ISO)指定为国际标准,是国际上使用最广泛的一种字符编码。
在计算机中,每个ASCII码字符可存放在一个字节中,最高位(d7)为校验位,用“0”填充,后7位为编码值,如表1-2所示。
表1-2 ASCII码表
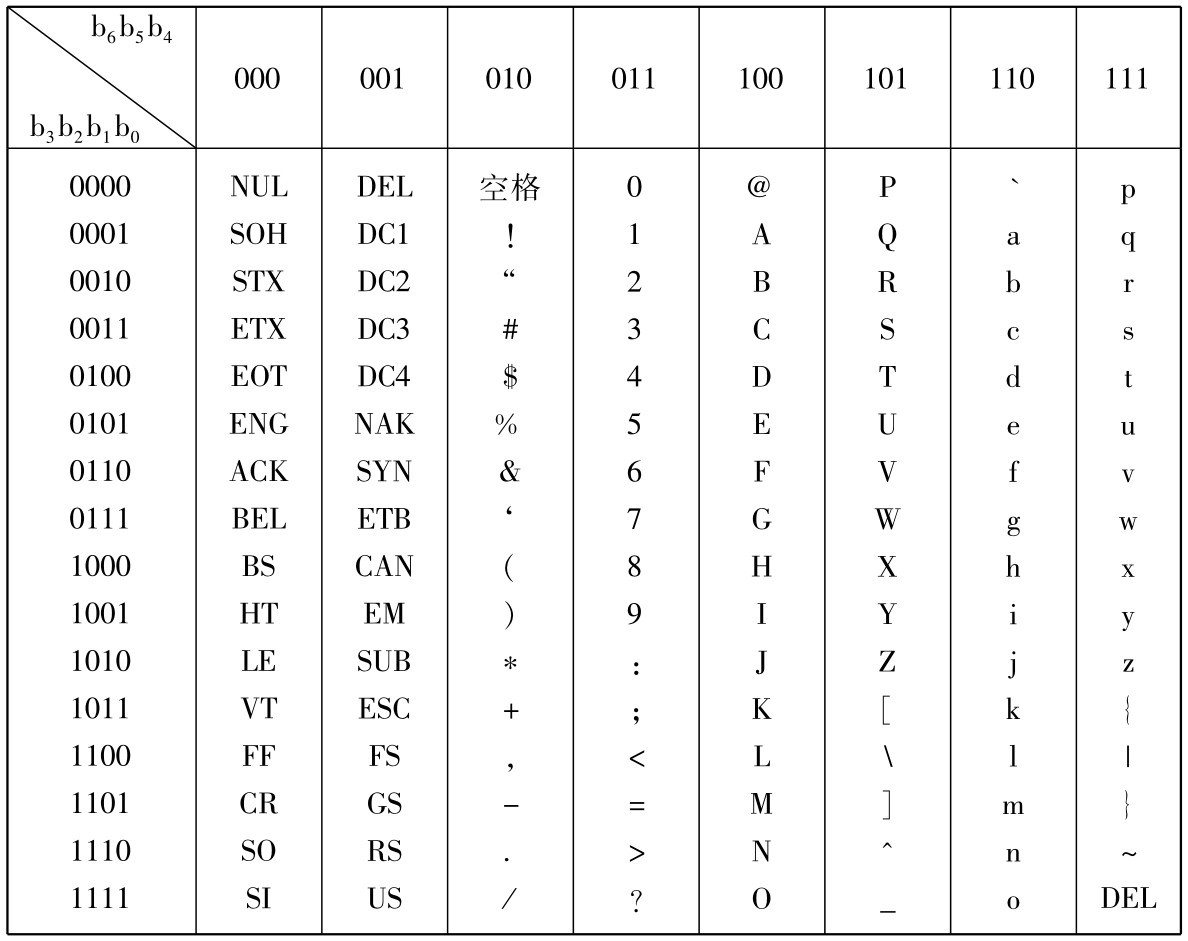
值得注意的是:在ASCII码表中,3组常用字符---阿拉伯数字、大写英文字母、小写英文字母,它们的ASCII码值都是分别连续递增的。 也就是说,知道了每组字符中的第一个字符的ASCII码值,则该组中的其他字符的ASCII码值都是可以计算出来的。 例如,若已知字符“A”的ASCII码值为65,则字符“E”的ASCII码值为69,字符“J”的ASCII码值为74。
前面介绍的7位ASCII码,称为基本ASCII码。 若用8位编码的ASCII码,共有28=256个字符,称为扩展ASCII码,主要是能增加字符使用数量。
(2)汉字编码。 文字(字符、汉字)信息的编码体系包括机内码、输入码、字形码、交换码、地址码和控制码。 其中最主要的是机内码、输入码和字形码。
英文为拼音文字,所有的字均由26个字母拼组而成,加上数字等其他符号,常用的字符仅有95种,所以ASCII码采用7bit编码已经够用,一个字符只须占一个字节。 汉字为非拼音文字,如果一字一码,2000个汉字需要2000种码才能区分。 显然,汉字编码比英文字符编码要复杂得多。
①国标码。 1981年,我国颁布了用于信息处理的汉字国家标准---《中华人民共和国国家标准(GB2312-80)信息交换用汉字编码字符集·基本集》,该标准常称为GB2312-80汉字编码标准,简称为汉字国标,它是汉字交换码的国家标准,所以又称“国标码”。 该标准收入了6763个常用汉字(其中,一级常用汉字3755个,二级不常用汉字3008个),以及英、俄、日文字母与其符号682个,共有7445个符号。 任何汉字编码都必须包括该标准规定的这两级汉字。
GBK码是新的国标码,是扩展的汉字国家标准(GB30001-94.1),该标准简称为GBK国标。 GBK码除包含了GB2312码外,还收录了其他20982个汉字,因此,现在国标码是指GBK码。
国标码规定,每个字符由一个2字节代码组成。 每个字节的最高位恒为“0”,其余7位用于组成各种不同的码值,如图1-1所示。

图1-1 汉字国标码的编码格式
两个字节的代码,共可表示128×128=16384个符号,而国标码的基本集目前仅有7000多个符号,所以足够使用。
②汉字机内码。 机内码是计算机内部进行文字(字符、汉字)信息处理时使用的编码,简称内码。 当文字信息输入到计算机中后,都要转换为机内码,才能进行各种处理:存储、加工、传输、显示和打印等。 对一种文字,其机内码是唯一的。
计算机既要处理汉字,也要处理英文。 为了实现中、英文兼容,通常利用字节的最高位来区分某个码值是代表汉字或ASCII码字符。 具体的做法是,若最高位为“1”视为汉字符,为“0”视为ASCII字符。 所以,汉字机内码可在上述国标码的基础上,把两个字节的最高位一律由“0”改“1”而构成。 例如,汉字“大”字的国标码3473H,两个字节的最高位均为“0”。 把两个最高位全改成“1”,变成B4F3H,就可得“大”字的机内码。 由此可见,同一汉字的汉字国标码与汉字机内码内容并不相同,而对ASCII字符来说,机内码与国标码的码值是一样的。 汉字机内码是变形的国标码,这种变形又正好将中文和英文区分开来。
③汉字输入码(外码)。 汉字输入曾经是应用计算机进行汉字处理的瓶颈,近年来,经过人们悉心研究,现已有了键盘输入、语音输入和字形识别3种输入方法。 其中,目前仍以键盘输入使用最普遍。 汉字输入码是汉字信息由键盘输入计算机时使用的编码,简称外码,通过使用键盘的字母键和数字键编码输入汉字。 每一种键盘汉字输入法都有相应的编码方法,可以划分为流水码、音码、形码和音型结合码4种类型。
实际上不管使用何种输入法,在输入码与机内码之间都存在着一个对应关系,很容易通过“输入管理程序”把输入码转换为机内码。 可见输入码仅是供用户选用的编码,故也称为“外码”,而机内码则是供计算机识别的“内码”,其码值是唯一的。 二者通过键盘管理程序来转换,如图1-2所示。

图1-2 从外码到内码的转换
④汉字字形码。 汉字字形码是指汉字字形存储在字库中的数字化代码,用于计算机显示和打印输出汉字的“形”,即字形码决定了汉字显示和打印的外形。 字形码是汉字的点阵表示,称为“字模”。 同一文字符号,可以有多种“字模”,也就是字体或字库。
显示/打印文字时还要用到汉字字形码。 通常汉字显示使用16×16点阵,如图1-3所示给出了汉字“阿”字点阵构成示意图。 汉字打印可选用24×24、32×32、48×48等点阵。

图1-3 “阿”字的点阵构成
综上可知,无论英文字符还是中文字符,在机内一律用二进制编码来表示。 但因汉字字符和英文字符数量悬殊,所以后者可采用单字节码,前者必须采用双字节码。 又因二者共用一个存储器,导致汉字内码不同于它的交换码;二者要共用同一键盘,使汉字不得不实行编码输入。 汉字库占用的空间,也远比英文字库(称为字符发生器)大。 汉字处理较纯英文处理需要更多的时间与空间。
(3)英文字符的全角与半角。 英文字符存储用一个字节,汉字用两个字节,早期显示时英文字符用8×16点阵,汉字用16×16点阵,即显示时汉字比英文字符宽一倍,在中文处理时会有半边汉字,出现不整齐的现象,与通常的中文方格不一致,于是在汉字编码时,把所有英文字符又按汉字编码方式再一次编码,仍是两个字节存储,显示和汉字一样宽,并把中文特有的标点符号如空心句号也进行了处理。 这样显示时就和习惯一致了。 汉字编码方式的英文字符称为英文字符的全角符号,ASCII编码方式的英文字符称为半角符号。
【思考题】
(1)在计算机内部采用什么进制? 为什么?
(2)完成下列各数的进制转换。
(10101001.101011)2=( )10=( )8=( )16
(A8D)16=( )10=( )8=( )2
(3)计算机的最小数据单位是什么,基本单位是什么?
(4)找几个硬盘、U盘、内存,查看其容量单位和大小。
(5)在计算机中找几个文件,查看其大小分别是多少。
(6)完成下列单位的换算。
4GB=( )MB=( )KB=( )B



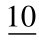
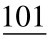
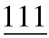
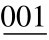 (整数分组,不足3位,可不补0)
(整数分组,不足3位,可不补0)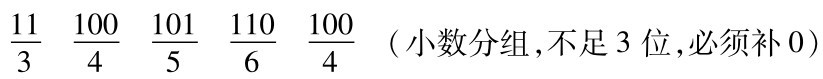

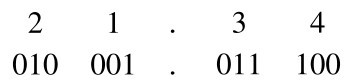
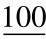
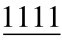 .
.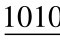 )
)


