7.4 习题解答
1.解:设入射的自然光的光强为I0,将自然光分解成p方向和s方向的两束线偏振光,两束光的强度相等。
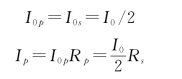
反射系数为
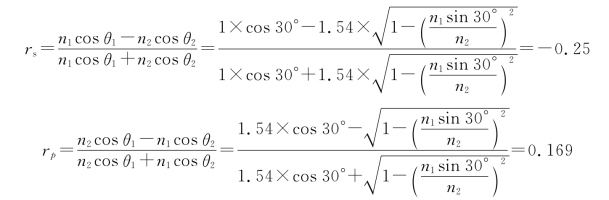
故偏振度为
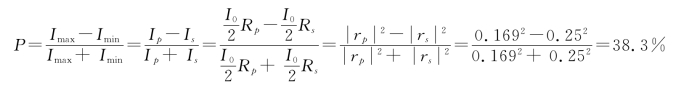
2.解:如图7-20所示,线偏振光射入方解石晶体后,电矢量被分解为垂直于主平面的o振动和平行于主平面的e振动,主平面是通过e轴垂直纸面的。
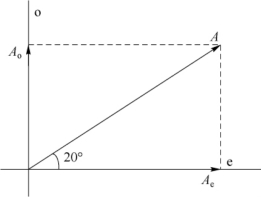
图7-20 线偏振光射入方解石晶体后的分解示意图
设入射光线偏振的振幅为A,则o光、e光的振幅分别为
Ao=Asin 20°=0.34A
Ae=Acos 20°=0.94A
两者之比为
Ao/Ae=tan 20°=0.36
在考虑两束光的强度问题时,应注意光强与折射率成正比,而且e光的折射率与传播方向有关,因此,o光和e光的强度分别为
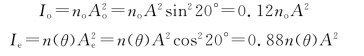
强度之比为
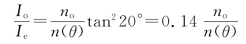
式中θ为e光法线速度和光轴的夹角,如光轴与晶体表面平行,则有
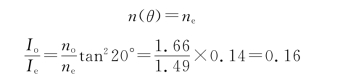
3.解:由马吕斯定律可知,通过第二个尼科耳棱镜后的光强为
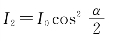
式中α为两尼科耳棱镜主截面的夹角,当α=30°时,得
I2=3I0/8
当α=45°时,得
I2=I0/4
4.解:①因为光束正入射,所以o光不发生偏折,e光的偏向角α与e光波法线和光轴夹角θ的关系为为求最大偏向角,令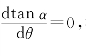 得
得
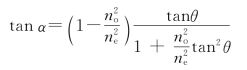
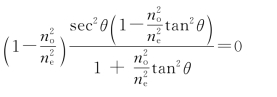
解得

所以,当晶片表面与光轴成90°-45°9′59″=44°50′1″角度时,e光的偏向角最大。
②e光的最大偏向角为
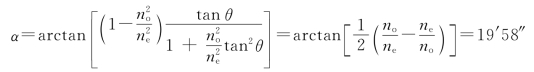
5.解:在此特殊情况下,o光和e光在晶体内的传播方向均服从普遍的折射定律,即
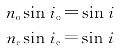
将no=1.658 36,ne=1.486 41,i=50°代入,分别算出
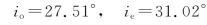
两束光在晶体中的夹角为
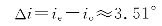
6.解:①o光遵守折射定律,因此它将不偏折地通过晶片。由惠更斯作图法可知,e光波法线的方向与o光的相同,因此
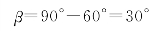
由
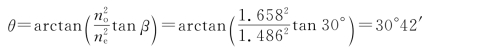
得到o光线和e光线的夹角为
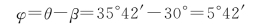
②如图7-21所示。由于o光线和e光线都在图面内,所以图面是o光线和e光线的共同主平面。o光的振动方向垂直于图面,以黑点表示;e光的振动方向在图面内,以线条表示。
③e光在法线沿β方向传播时的折射率
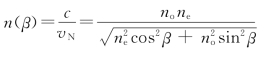
于是
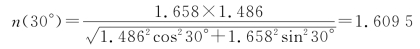
因此,o光和e光通过晶片后的相位差为
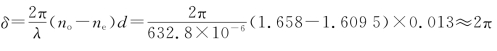
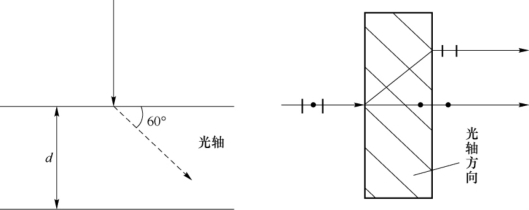
图7-21 经过晶体后o光和e光的示意图
7.解:根据射线速度倾角(与光轴的夹角)ξ和法线速度倾角θ的关系
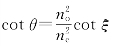
直接写出两者夹角α的公式
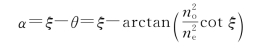
为求α的极值,令
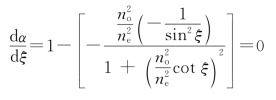
整理得
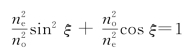
由此解出偏离角α出现极大的条件为
cotξ=ne/no或cotθ=no/ne
以钠黄光为例,把no=1.658 36,ne=1.486 41代入上式,算得
am≈6.26°
8.解:这时入射角i≈90°,故sini≈1。在此特殊情况下,o光和e光在晶体内的传播方向均服从普遍的折射定律,求得折射角io和ie;再分别求出o、e两光线射向平板对面的位置坐标(如图7-22所示):
xo=dtanio, xe=dtanie
最后算出两点间隔为
Δx=xo-xe=d(tanio-tanie)≈12.7μm
9.解:如图7-23所示,由于光轴垂直于入射面,所以e光和o光的波面与入射面的截线均为圆形。从图7-23中容易看出,对于入射光与光轴所成入身角θ1,存在相应的e光折射角θ2e,且有
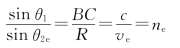
式中,R是e光波的圆截线的半径。由于c/ve是一常数,即在本题目描述的特殊情况下,e光
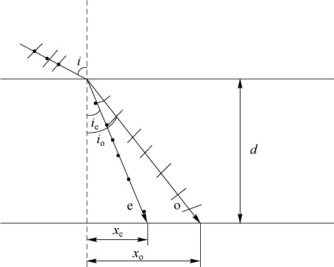
图7-22 o光和e光在晶体内的传播
遵守普通的折射定律(实际上,对于e光,只有当光轴垂直于主截面时才能运用折射定律),其折射方向由上式给出,因此,当θ1=60°时,e光的折射角为
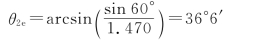
而o光的折射角为
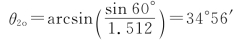
因此,o光和e光的夹角为
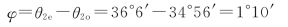
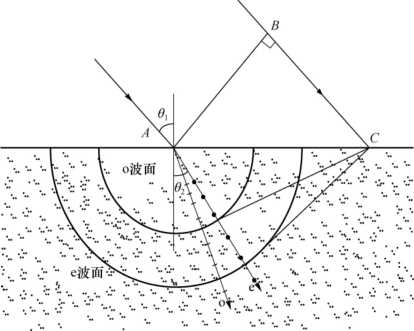
图7-23 o光和e光在晶体内的传播
10.解:如图7-24所示,在中间界面上发生的折射情形是,光线1由折射率ne→no,光线2由折射率no→ne,入射角均为α,折射角分别设为i1和i2。此时,两光线在第二块棱镜中的传播方向仍由通常的折射定律确定。取no=1.658 36,ne=1.486 41,算出
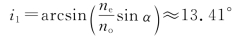
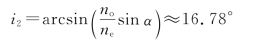
再考虑1、2两条光线在右侧界面的折射情形,根据几何关系,此时的入射角分别为
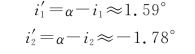
相应的折射角为
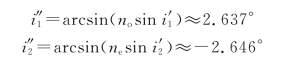
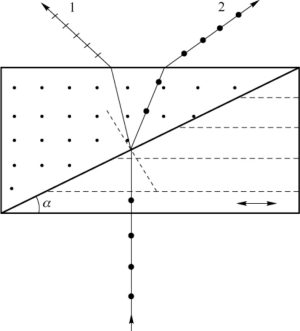
图7-24 光线经过沃斯拉顿棱镜后的情况
11.解:如图7-15所示,对于石英晶体,no=1.544 24,ne=1.553 35。o光波的折射角为
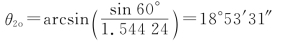
且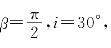 则e光波的折射角为
则e光波的折射角为
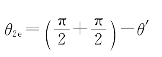
其中
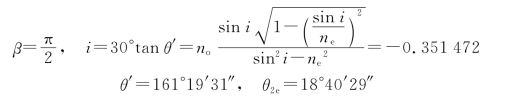
因此,o光线和e光线的夹角为α=θ2o-θ2e=13′2″。
12.解:λ/4波片的最小厚度d应满足
(no-ne)d=±λ/4
就λ=5 892.90×10-10 m的钠黄光来说,对于方解石有
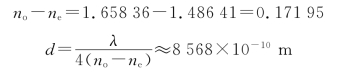
13.解:如图7-16所示,光束垂直入射在第一块晶体时,o光和e光以同一速度传播且不分开。经过两棱镜的界面时,对于o光,由于界面左右棱镜的折射相同,所以不发生偏折,到达棱镜-空气界面时是正入射,故o光仍不发生折射。因此,o光沿水平方向穿过塞拿蒙棱镜。对于e光,在两棱镜的界面,入射角为20°,由折射定律得
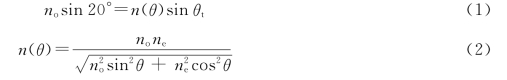
其中,θ是e光波法线与光轴的夹角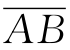 与
与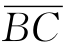 的夹角),θt是e光波法线与光轴的夹角
的夹角),θt是e光波法线与光轴的夹角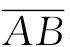 与
与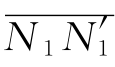 的夹角),且
的夹角),且

联合式(1)、式(2)和式(3),得
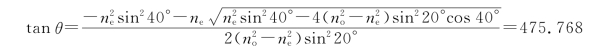
其中
no=1.544, ne=1.553
因此
θ=89°52′46″, n(θ)=1.553
在棱镜-空气界面,法线为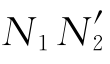 ,入射角为
,入射角为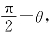 并设空气的折射率为1,折射角为θ,则t
并设空气的折射率为1,折射角为θ,则t
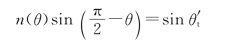
由于在空气中波法线与光线重合,且o光波沿水平方向出射,所以o光线和e光线之间的夹角为θt=11′13″。
14.解:如图7-25所示,设线偏振光的振幅为A0,其振动方向与晶体主截面的夹角为α,与尼科耳棱镜主截面的夹角为β,线偏振光经方解石后分解为e振动和o振动,其振幅分别为
Ae=A0cosα, Ao=A0sinα
各自通过尼科耳棱镜后的振幅分别为
A1=Aecos(α+β)=Aocos(α+β)cosα
A2=Aosin(α+β)=Aosin(α+β)sinα
15.解:①椭圆偏振光可视为两个位相差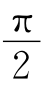 的光矢量分别沿长短轴方向的线偏振光的合成。如图7-26所示,设长短轴的方向分别是y轴和x轴。
的光矢量分别沿长短轴方向的线偏振光的合成。如图7-26所示,设长短轴的方向分别是y轴和x轴。
依题意,插入快轴平行于x轴的1/4波片后,透射光为线偏振光,其振动方向与x轴成70°夹角,因而沿y方向振动的光矢量沿x方向振动的位相差变为零。由于快轴沿x轴的1/4波片产生y方向的振动相对x方向的振动有-π/2的位相延迟角,所以椭圆偏振光的y方向振动相对x方向振动有π/2的位相差。这是左旋椭圆偏振光。
②由图7-26可见,椭圆长短轴之比为Ay/Ax=tan70°=2.747。
16.解:如图7-27所示,部分偏振光的光强极大Imax的方位总是正交的。任意斜方位与的光强I(α)是Imax和Imin的非相干叠加,即
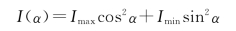
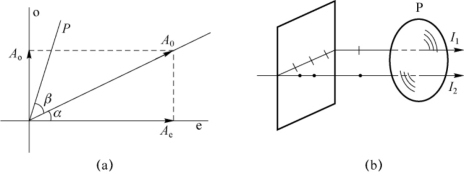
图7-25 o光和e光的振幅及光强示意图
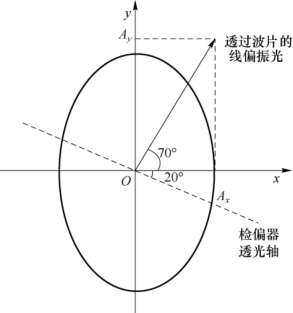
图7-26 椭圆偏振光分解为两个线偏振光
当α=60°时,I(α)=Imax/2,代入上式求出
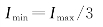
因此,该部分偏振光的偏振度为
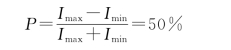
17.解:用偏振光干涉的方法求解,如图7-28所示。
对通过第一块尼科耳棱镜N1的线偏振光的振幅A1作两次投影,得第二块尼科耳棱镜N2透振方向的两个振动的振幅A2e、A2o,其值分别为
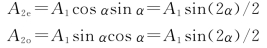
再仔细分析这两个振动之间总的相位差
δ=δ1+δ2+δ3
式中δ1为λ/4片入射点处o、e的振动相位差,δ1=π;δ2为晶片体内传播附加的相位差,δ2=±π/2(我们取δ2=+π/2);δ3为o轴、e轴正向朝N2方向投影的相位差,δ3=0。所以
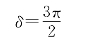
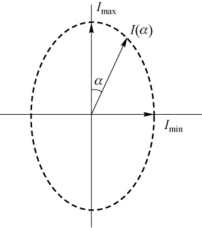
图7-27 用尼科耳棱镜观察部分偏振光
最后通过N2的光强I2是A2e、A2o相干叠加的结果,即
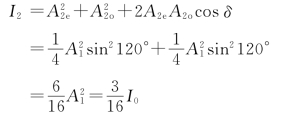
如果取δ2=-π/2,上式等号右边第三项(交叉项)仍然为零,I2不变。
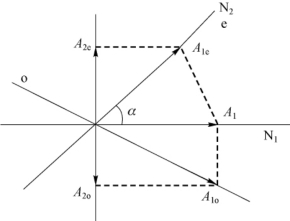
图7-28 偏振光干涉法的分析示意图
18.解:如图7-29所示,光强为I0的自然光经第一个尼科耳棱镜N1后,成为线偏振光且振幅为A1,则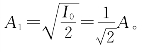
从波片出射的o光和e光的振幅分别为
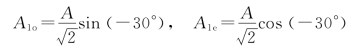
经第二个尼科耳棱镜N2后,o光和e光的振幅分别为
A2e=A1ecos 40°=0.455A, A2o=A1ocos 50°=-0.225A
因插入了1/8波片,两相干线偏振光的位相差 所以系统的出射强度为
所以系统的出射强度为
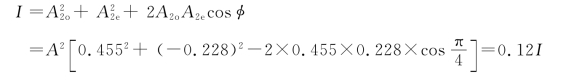
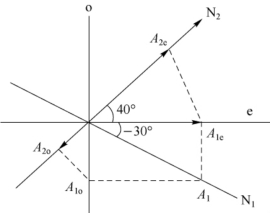
图7-29 将1/8波片插入前后放置的尼科耳棱镜中间时光线的传播
19.解:①自然光通过第一块尼科耳棱镜后成为线偏振光,再通过λ/4片后成为(正)椭圆偏振光。
②用偏振光干涉的方法求此椭圆偏振光通过第二块尼科耳棱镜P2的光强,为此分别求出振幅,如图7-30所示。
Ae2=Aecos 30°=A1cos230°
Ao2=Aosin 30°=A1sin230°
投影于P2方向的两个扰动的相位差为
δ=δ1+δ2+δ3
式中δ1为λ/4入射点的相位差,δ2为晶片体内传播的附加相位差,δ3为由o光和e光组成的坐标系正向朝P2投影引起的相位差
δ1=π, δ2=±π/2, δ3=0
故
δ=π±π/2
于是出射光强为
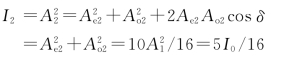
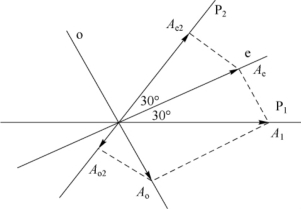
图7-30 椭圆偏振光经过两个尼科耳棱镜后的传播
20.解:如图7-31所示,此系统会产生偏振干涉。
设入射光的光强为I0,经P2后光强为
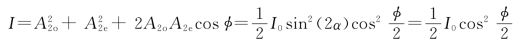
其中α=45°,两相干线偏振光的位相差是
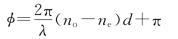
又当φ=(2m+1)π,m=0,1,2,…时,干涉相消,对应波长的光不能透过这一系统。对方解石有ne=1.658 4,no=1.486,因此,不能透过这一系统的光波的波长为
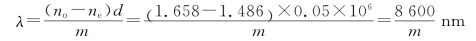
可见光的范围为390~780nm,所以下列波长的光不能透过这一系统
m=11,λ=782nm;m=12,λ=717nm;m=13,λ=662nm
m=14,λ=614nm;m=15,λ=573nm;m=16,λ=538nm
m=17,λ=506nm;m=18,λ=478nm;m=19,λ=453nm
m=20,λ=430nm;m=21,λ=410nm;m=22,λ=391nm
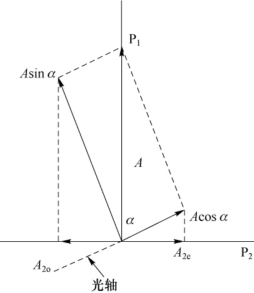
图7-31 偏振干涉示意图
21.解:由旋光率α与折射率差Δn的关系
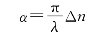
得
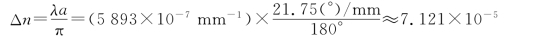
22.解:①当两尼科耳棱镜主截面正交时,为消除黄绿色光,应使该波长的光在通过石英旋光晶片后,偏振面旋转180°,即
ψ=ad=180°
由此得
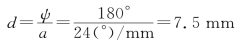
即当晶片厚度d=7.5k mm(k=1,2,…)时都可对此波长消光。
②当两尼科耳棱镜的主截面平行时,应满足
ψ=ad=90°
由此得
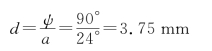
即当晶片厚度d=3.75k mm(k=1,3,…)时都可对此波长消光。
23.解:第一块棱镜的光轴与表面平行。如图7-32所示,当自然光正入射时,两折射光线的传播方向均垂直于表面(和光轴),方向并不分离,但波速vo和ve不同(由于冰晶石是负晶体,vo<ve)。进入第二块棱镜,由于光轴垂直于入射面,光线的传播方向服从普通的折射定律,只是折射率应取主折射率no和ne。对于平行纸面的振动,折射率由ne变到no。因no>ne,所以光线朝第二块棱镜底面的方向偏折。对于垂直纸面的振动,折射率由no变到ne(折射率变小),所以光线朝着背离第二块棱镜底面的方向偏折。出射棱镜后,由于空气的折射率比no和ne都要小,光线将进一步朝相反的方向偏折。
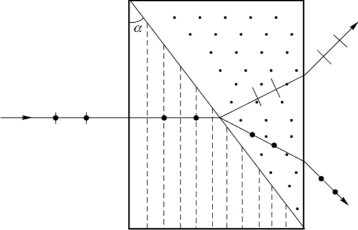
图7-32 沃拉斯顿棱镜中双折射光线的传播
24.解:如图7-33所示,用惠更斯作图法可见,在晶体光轴方向与表面成一定夹角时,尽管入射光线与光轴方向平行,但是晶体内的光线仍然发生了双折射。无论是在传播方向上,还是在传播速度上,o光和e光都发生了分离。必须注意,仅当体内光线沿光轴方向传播时,才不发生双折射。显然要保证体内折射光线与光轴方向一致,只有光轴垂直于晶体表面,且令平行光正常入射才行。
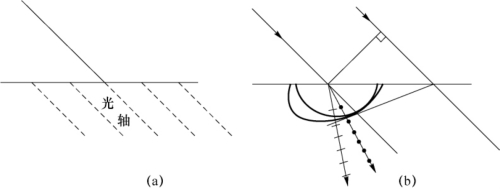
图7-33 利用惠更斯作图法进行分析
25.解:见图7-34(b),自然光正入射到棱镜A前,o光和e光不分开,o光经反射后以平行光轴的方向出射,设e光波的法线(沿AD方向)与光轴的夹角为θe,则e光波的法线与界面法线AN的夹角为反射角,即45°-θe。
由反射定律得
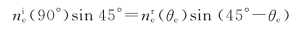
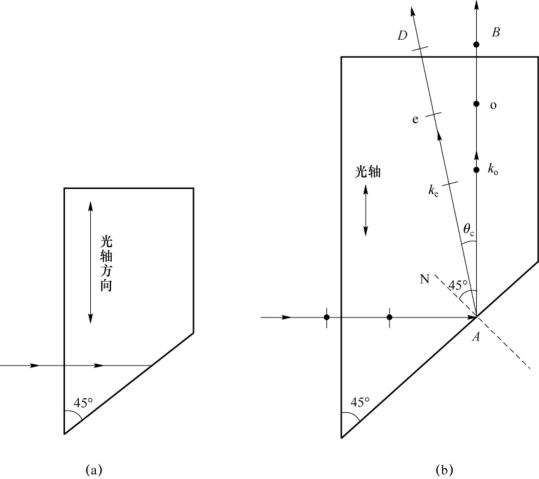
图7-34 光在负单轴晶体做成的棱镜中的传播
而
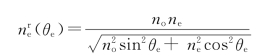
考虑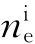 (90°)=ne,上述两式消去
(90°)=ne,上述两式消去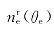 后,整理得
后,整理得
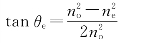
因此,e光线与光轴的夹角θ′e为
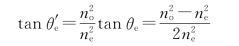
o光和e光的光路及其振动方向见图7-34(b)。
26.解:我们可以根据e光的折射方向来判断晶体的正负。如图7-35(c)所示,假定晶体是负的,则晶体中的e光次波面是长轴垂直光轴的椭球面。由惠更斯作图法可知,e光向上偏折。由此可以判定在图7-35(a)的折射情形中,晶体是负的;同理,在图7-35(b)的折射情形中,晶体是正的。
27.解:本题是光在单轴晶体中的双折射问题。光在棱镜内及射出棱镜后,双折射光线的传播方向和振动方向如图7-36(b)所示。当自然光入射到第一块棱镜时,光轴与晶体表面垂直,不发生双折射。进入第二块棱镜后,对于o光,两棱镜的折射率都是no,它仍原方向前进,根据折射定律,最后出射时也不发生偏折。对于e光,两棱镜的折射率不同,在其界面上要发生偏折,但不服从普通的折射定律,折射光的方向由惠更斯作图法确定,如图7-36(c)所示。
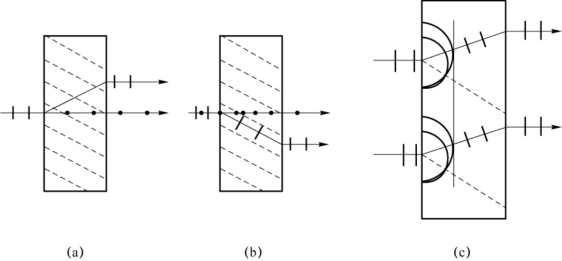
图7-35 光线经过晶体后的两种传播情形及惠更斯作图法
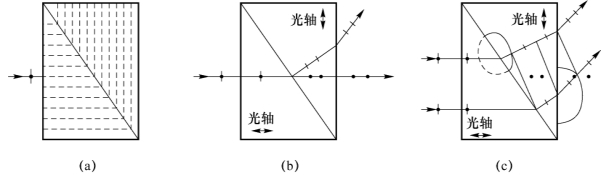
图7-36 光在单轴晶体中的双折射
28.解:首先,自然光入射到第一块偏振片上时,出射的是线偏振光。再经λ/4片后,出射的一般是椭圆偏振光(特殊情况下是圆偏振光或线偏振光,具体由λ/4片的光轴方向和第一块偏振片的透振方向的相对取向决定)。最后从第二块偏振片出射的是线偏振光,强度随λ/4片的转动而变,有极大和消光现象。当λ/4片的光轴与第一块偏振片的透振方向成45°角时,从λ/4片出射的是圆偏振光,从第二块偏振片出射的光的强度为极大。当λ/4片的光轴平行或垂直于第一块偏振片的透振方向时,从λ/4片出射的为线偏振光,偏振方向垂直于第二块偏振片的偏振方向,从而最后出射光的强度为零,有消光现象。
29.解:仅用一块偏振片是无法区别椭圆偏振光和部分偏振光的,必须借助于λ/4片。令入射光依次通过λ/4片和第二块偏振片,并保证λ/4片的光轴方向对准入射光的强度极大或极小方位(对椭圆偏振光来说,即主轴方位)。再转动第二块透振片的透振方向,观察出射光的强度变化:如有消光现象,则为椭圆偏振光;如无消光现象,则为部分偏振光。实验的关键是保证λ/4片的光轴对准入射光的极大或极小方位,用以下方案可以实现。
①用第一块偏振片对准入射光,转动其振动方向,观察透射光的强度变化。当强度极大或者极小时,停住转动。这时,此偏振片已对准入射光的极大或极小方位。
②在第一块偏振片后加第二块偏振片,并转动后者的透振方向,观察透射光的强度变化,必有极大和消光位置。在消光位置停住,转动第二块偏振片,这时必然有两块偏振片的透振方向互相垂直。
③在两块偏振片之间插入λ/4片,透射光的强度一般不为零。转动λ/4片,可观察到4个消光方位,任选一个方位停住λ/4片。这时,已保证λ/4片的光轴对准入射光的极大或者极小方位(椭圆偏振光的主轴方位)。
④撤去第一块偏振片,并保持λ/4片不动。这时,转动第二块偏振片即可检验椭圆平偏振光。
30.解:①补偿器使o光和e光之间产生的相位差为
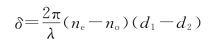
又由于两线偏振器正交,且补偿器光轴与线偏振器透光轴成45°角,所以透过第二块偏振器的光强为
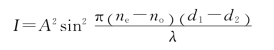
因此,暗纹条件为
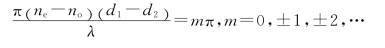
当m=0时,d1=d2处有一暗纹;当m=1时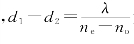 为相邻另一暗纹出现的位置。从图7-37所示的几何关系可得暗纹的间距为
为相邻另一暗纹出现的位置。从图7-37所示的几何关系可得暗纹的间距为
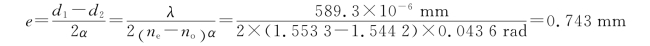
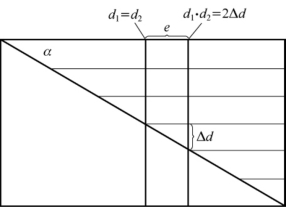
图7-37 巴比涅补偿器放在两正交线偏振器之间时产生明暗纹的几何关系
②设方解石波片的厚度为x,由于放上方解石波片,所以o光和e光之间位置相差的改变为
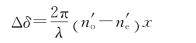
式中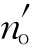 =1.658 4
=1.658 4 =1.486 4。由于相差的改变使条纹移动了1/2条纹间距,因此Δδ=π,所以
=1.486 4。由于相差的改变使条纹移动了1/2条纹间距,因此Δδ=π,所以
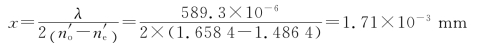
31.解:是右旋偏振光。因为在以1/4波片快轴为y轴的直角坐标系中,偏振片位于Ⅱ、Ⅳ象限时消光,说明圆偏振光经1/4波片后,成为位于Ⅰ、Ⅲ象限的线偏振光,此线偏振光由y方向振动相对x方向振动有2π位相差的两线偏振光合成。而1/4波片使e光、o光的位相差增加π/2,成为2π,所以,进入1/4波片前y方向振动相对x方向振动就已有3π/2的位相差,所以是右旋偏振光。
32.解:如图7-38所示,所谓以“最小偏向角入射”,即选取合适的入射角,使光线经第一折面后平行于棱镜的底边,本题棱镜底边平行于光轴,故光线在水晶棱镜内部沿光轴传播,它将被分解为左旋光和右旋光,折射率分别为nL和nR(nR<nL);经第二折射面后就有不同的偏向角δL和δR,考虑在第二个折射面右旋光和左旋光的入射角近似于90°-60°=30°,应用折射定律有
nRsin 30°=siniR, nLsin 30°=siniL
由此得
siniL-siniR=(nL-nR)/2
即
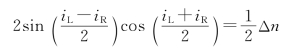
其中
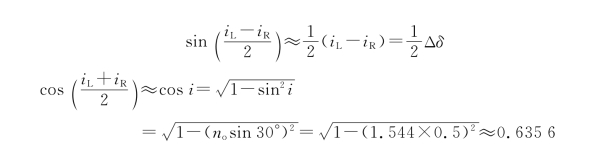
其中,Δn=7.121×10-5。最后得到出射的两束左、右旋圆偏振光传播方向之间的夹角为
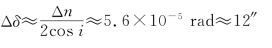
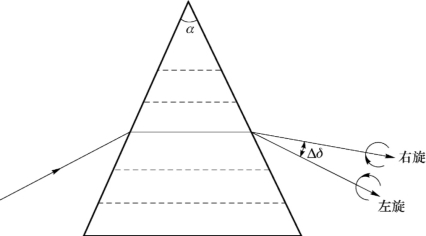
图7-38 钠光以最小偏向角条件射入顶角为60°的石英晶体棱镜
33.解:如图7-39所示,使第二偏振片的透振方向与平面偏振光的振动方向保持垂直,并且第一片的透振方向与平面偏振光的振动方向不垂直即可。
如果第一片与平面偏振光的振动方向的夹角为θ,则由马吕斯定律可得
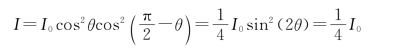
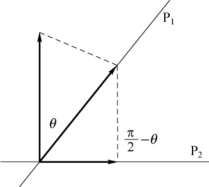
图7-39 两片偏振片与偏振光之间的关系
34.证明:如图7-40所示,当第三个偏振片P与第一个偏振片P1的透振方向的夹角为θ=ωt时,P、P之间的夹角为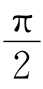 -θ,于是可得从P透射的光强为
-θ,于是可得从P透射的光强为
22
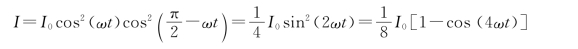
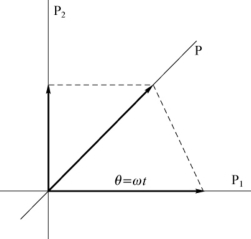
图7-40 3个偏振片之间的关系示意图
35.解:由于反射光有半波损失,即反射瞬间,两振动分量都反向,如图7-41所示。逆着反射方向看,若入射光是左旋的,y分量的相位比x分量的相位超前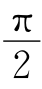 。观察反射光时,依然是y分量的相位比x分量的相位超前
。观察反射光时,依然是y分量的相位比x分量的相位超前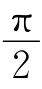 ,但由于x轴方向相反,相当于y分量比x分量超前
,但由于x轴方向相反,相当于y分量比x分量超前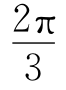 ,则反射光是右旋的。
,则反射光是右旋的。
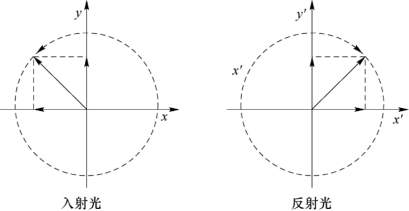
图7-41 入射光和反射光的偏振示意图
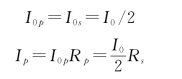
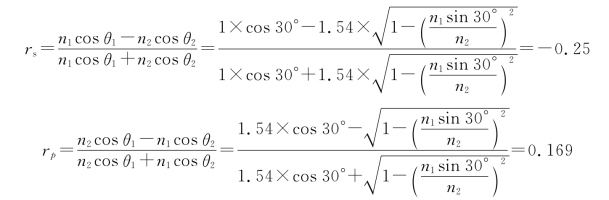
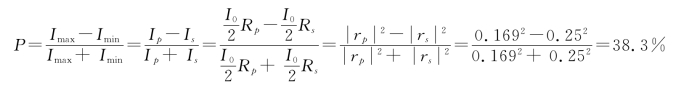

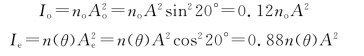
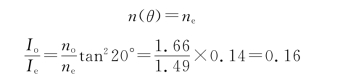
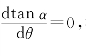 得
得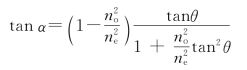
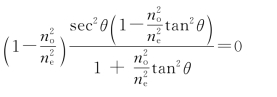
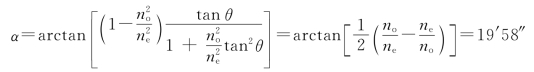
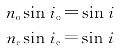
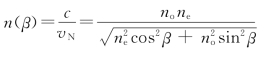
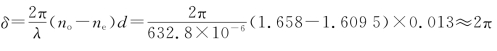

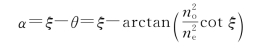
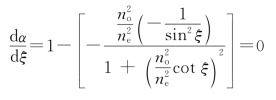
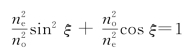


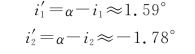
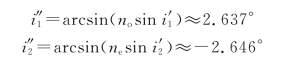

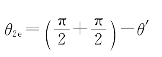
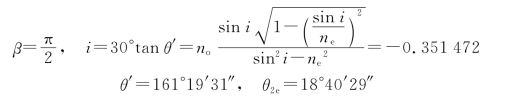
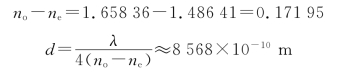
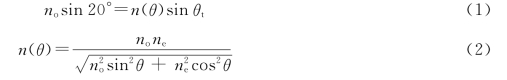
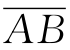 与
与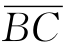 的夹角),θ
的夹角),θ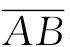 与
与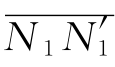 的夹角),且
的夹角),且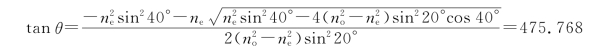
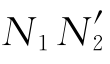 ,入射角为
,入射角为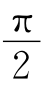 的光矢量分别沿长短轴方向的线偏振光的合成。如图7-26所示,设长短轴的方向分别是y轴和x轴。
的光矢量分别沿长短轴方向的线偏振光的合成。如图7-26所示,设长短轴的方向分别是y轴和x轴。

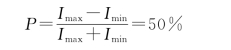
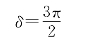

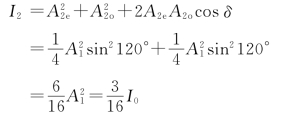

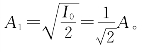
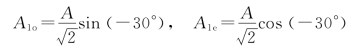
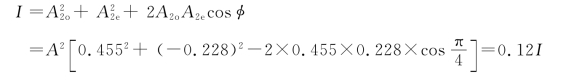

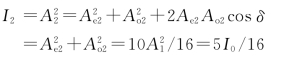


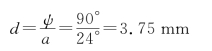



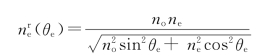
 (90°)=n
(90°)=n

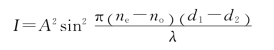

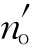 =1.658 4
=1.658 4 =1.486 4。由于相差的改变使条纹移动了1/2条纹间距,因此Δδ=π,所以
=1.486 4。由于相差的改变使条纹移动了1/2条纹间距,因此Δδ=π,所以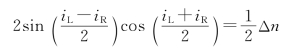
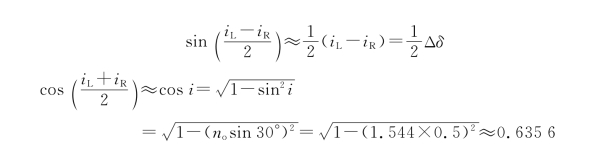

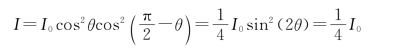

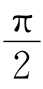 -θ,于是可得从P透射的光强为
-θ,于是可得从P透射的光强为
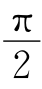 。观察反射光时,依然是y分量的相位比x分量的相位超前
。观察反射光时,依然是y分量的相位比x分量的相位超前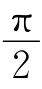 ,但由于x轴方向相反,相当于y分量比x分量超前
,但由于x轴方向相反,相当于y分量比x分量超前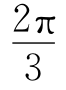 ,则反射光是右旋的。
,则反射光是右旋的。