-
1.1内容简介
-
1.2前 言
-
1.3第1章 几何光学基础
-
1.3.11.1 知识要点
-
1.3.21.2 典型例题
-
1.3.31.3 习 题
-
1.3.41.4 习题解答
-
1.4第2章 光波的描述
-
1.4.12.1 知识要点
-
1.4.22.2 典型例题
-
1.4.32.3 习 题
-
1.4.42.4 习题解答
-
1.5第3章 光的干涉
-
1.5.13.1 知识要点
-
1.5.23.2 典型例题
-
1.5.33.3 习 题
-
1.5.43.4 习题解答
-
1.6第4章 光的衍射
-
1.6.14.1 知识要点
-
1.6.24.2 典型例题
-
1.6.34.3 习 题
-
1.6.44.4 习题解答
-
1.7第5章 光栅光谱
-
1.7.15.1 知识要点
-
1.7.25.2 典型例题
-
1.7.35.3 习 题
-
1.7.45.4 习题解答
-
1.8第6章 傅里叶变换光学
-
1.8.16.1 知识要点
-
1.8.26.2 典型例题
-
1.8.36.3 习 题
-
1.8.46.4 习题解答
-
1.9第7章 光在晶体中的传播
-
1.9.17.1 知识要点
-
1.9.27.2 典型例题
-
1.9.37.3 习 题
-
1.9.47.4 习题解答
-
1.10第8章 光波与物质的相互作用
-
1.10.18.1 知识要点
-
1.10.28.2 典型例题
-
1.10.38.3 习 题
-
1.10.48.4 习题解答
-
1.11第9章 光的量子性
-
1.11.19.1 知识要点
-
1.11.29.2 典型例题
-
1.11.39.3 习 题
-
1.11.49.4 习题解答
1
大学物理光学学习指导书
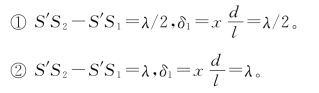
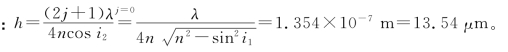
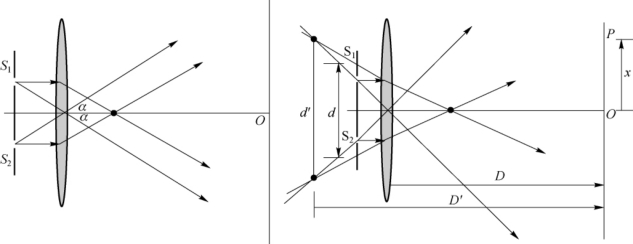
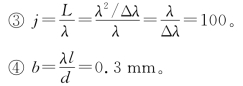
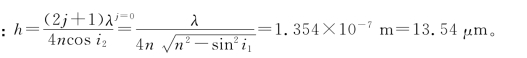
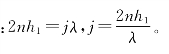 当h
当h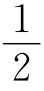 )λ,其圆环半径
)λ,其圆环半径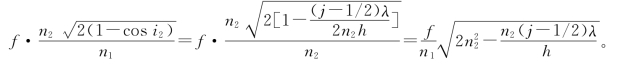
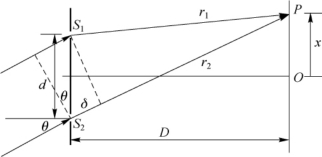
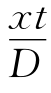 -tsinθ=(j+
-tsinθ=(j+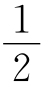 )λ,x=0,tsinθ=-(j+
)λ,x=0,tsinθ=-(j+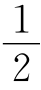 )λ,由于j可以取任意整数,同时又以小角度入射,θ≈sinθ=(j+
)λ,由于j可以取任意整数,同时又以小角度入射,θ≈sinθ=(j+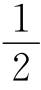 )
)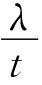 。
。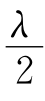 ,当Δm=20时
,当Δm=20时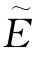 =aexp(i k),到达xy平面的球面波波前函数为
=aexp(i k),到达xy平面的球面波波前函数为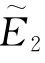 =aexp{i k[1+(x
=aexp{i k[1+(x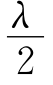 ,当Δm=20时
,当Δm=20时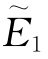 =Aexp(ik xsinθ),到达xy平面的球面波波前函数为
=Aexp(ik xsinθ),到达xy平面的球面波波前函数为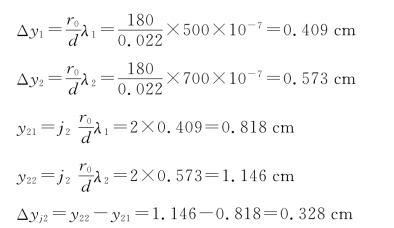
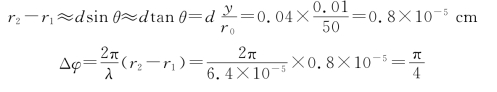
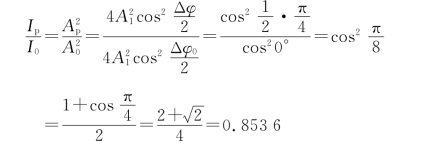
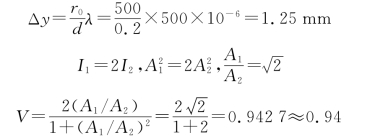
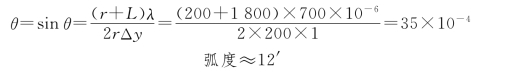
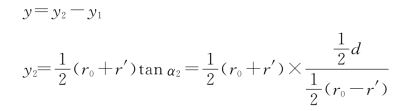
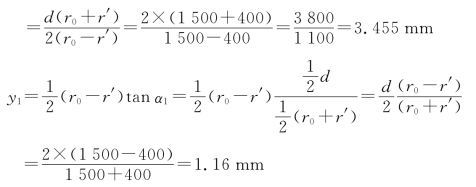
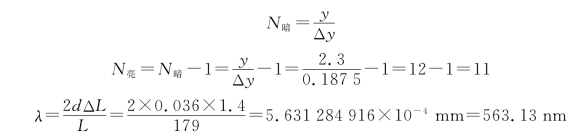
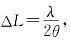 所以
所以