3.3　习 题

1.在杨氏双缝实验中，除了原有的光源缝S外，再在S的正上方开一狭缝S′，如图3－9所示。①若使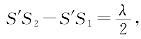试求单独打开S或S′以及同时打开它们时屏上的光强分布。

②若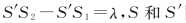同时打开时，屏上的光强分布如何？

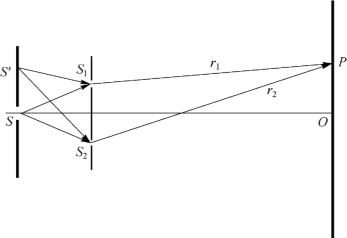
图3－9 杨氏双缝实验

2.瑞利干涉仪的结构和使用原理如下（参见图3－10）：以钠光灯作为光源置于透镜L1的前焦面，在透镜L2的后焦面上观测干涉条纹的变动，在两个透镜之间安置一对完全相同的玻璃管T1和T2。实验开始时，T2管充以空气，T1管抽成真空，此时开始观察干涉条纹。然后逐渐使空气进入T1管，直到它与T2管的气压相同。记下这一过程中条纹移过的数目。射光波长为589.3nm，管长为20cm，条纹移过98根，求空气的折射率。

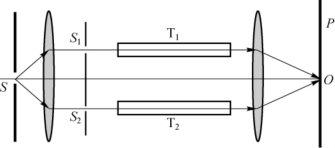
图3－10 瑞利干涉仪

3.如图3－11所示，将一焦距f′为50cm的会聚透镜的中央部分截取6mm，把余下的上下两部分再黏合在一起，成为一块透镜L。在透镜L的对称轴上，左边300cm处有一波长λ＝5×10－7 m的单色点光源S，在右边450cm处置一光屏DD。试分析并计算：

①S发出的光经过透镜L后的成像情况，如所成之像不止一个，计算各像之间的距离；

②在光屏DD上能否观察到干涉条纹？如能观察到干涉条纹，相邻明条纹的间距是多少？

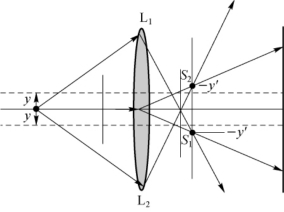
图3－11 习题3示意图

4.白光以45°角射在肥皂（n＝1.33）膜上，试求使反射光呈黄色（λ＝6.1×10－7 m）的最小膜厚度。

5.将光滑的平板玻璃覆盖在柱形平凹透镜上，如图3－12所示，试求：①用单色光垂直照射时，画出反射光中干涉条纹分布的大致情况；②若圆柱面的半径为R，且中央为暗纹，问从中央数第2条暗纹与中央暗纹的距离是多少？③连续改变入射光的波长，在λ＝5×10－7 m和λ＝6×10－7 m时，中央均为暗纹，求柱面镜的最大深度；④若轻压上玻璃片，条纹如何变化？

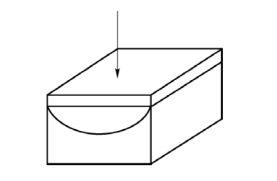
图3－12 习题5示意图

6.用很薄的云母片（n＝1.58）覆盖在双缝装置中的一条缝上，这时，光屏上的中心被原来的第7级亮纹所占据，若λ＝5.5×10－7 m，则云母片有多厚？

7.波长λ为0.5μm的平行单色光垂直入射到双孔平面上，已知双孔间距t为0.5mm，在双孔屏另一侧5cm远处，正放置一枚像方焦距f′为5cm的理想薄透镜L，并在L的像方焦平面处放置接收屏。求：①干涉条纹的间距等于多少？②将透镜往左移近双孔2cm，接收屏上干涉条纹的间距又等于多少？

8.在杨氏双缝实验中，双缝间距为0.5mm，接收屏距双缝1m，点光源距双缝30cm，它发射波长λ＝5×10－7 m的单色光。试求：①屏上干涉条纹间距；②若点光源由轴上向下平移2mm，屏上的干涉条纹向什么方向移动？移动多少？③如点光源发出的光波为500.0±2.5nm范围内的准单色光，求屏上能看到的干涉极大的最高级次；④若光源具有一定的宽度，屏上干涉条纹消失时，它的临界宽度是多少？

9.沿着与肥皂膜的法线成35°角的方向观察膜呈绿色（λ＝5×10－7 m），设肥皂水的折射率为1.33，求：①薄膜的厚度；②如果垂直注视，膜呈何种颜色？

10.一束白光垂直照射厚度为0.4μm的玻璃片，玻璃的折射率为1.5，在可见光谱范围内（λ＝4×10－7 m到λ＝7×10－7 m），反射光的哪些波长成分将被加强？

11.白光以45°角射在肥皂（n＝1.33）膜上，试求使反射光呈黄色（λ＝6.1×10－7 m）的最小膜厚度。

12.如图3－13所示的实验装置，在一洁净玻璃片的上表面放一滴油，当油滴展开成油膜时，在波长λ＝6×10－7 m的单色光的垂直照射下，从反射光中观察到油膜所形成的干涉条纹。在实验中由读数显微镜向下观察油膜所形成的干涉条纹。如果油膜的折射率n＝1.20，玻璃的折射率n′＝1.50，试求：①当油膜中心的最高点与玻璃片的上表面相距h＝1.2×10－6 m时，描述所观察到的条纹的形状，即可以观察到几条亮条纹，亮条纹所在处油膜的厚度是多少？中心点的明暗程度又如何？②当油膜逐渐扩展时，所看到的条纹将如何变化？

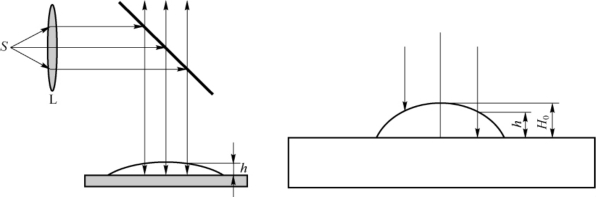
图3－13 习题12示意图

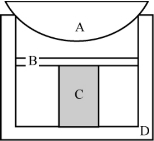
图3－14 习题13示意图

13.如图3－14所示，A为平凸透镜，B为平板玻璃，C为金属柱，D为框架，A、B之间留有气隙，而A被固定在框架的边缘上。温度变化时，C发生伸缩，而假设A、B、D都没有伸缩。现用波长为λ＝6.328×10－7 m的激光垂直照射，试求：①在反射光中观察时，看到Newton环的条纹都移向中央，这表明金属柱C的长度是增加还是缩短？②如果观察到有10个明条纹移到中央而消失，C的长度变化了多少毫米？

14.在傍轴条件下，等倾条纹的半径与干涉级有什么样的依赖关系？Newton环的情况又怎样？能够将两者进行区别吗？如何区别？

15.用钠光（λ＝5.893×10－7 m）观察Michelson干涉条纹，起初看到干涉场中有16个亮环，且中心是亮的。移动一个平面镜M1后，看到中心吞吐了20环，此时干涉场中还剩6个亮环。试求：①M1移动的距离；②开始时中心亮斑的干涉级；③M1移动后，最外面亮环的干涉级。

16.将光滑的平板玻璃覆盖在柱形平凹透镜上，如图3－15所示，试求：①用单色光垂直照射时，画出反射光中干涉条纹分布的大致情况；②若圆柱面的半径为R，且中央为暗纹，问从中央数第2条暗纹与中央暗纹的距离是多少？③连续改变入射光的波长，在λ＝5×10－7 m和λ＝6×10－7 m时，中央均为暗纹，求柱面镜的最大深度；④若轻压上玻璃片，条纹如何变化？

图3－15 习题16示意图

17.设Fabry－Poret腔（F－P腔）长5cm，用扩展光源做实验，光波波长λ＝6×10－7 m，问：①中心干涉级数是多少？②在1°的倾角附近，干涉环的半角宽度是多少？（设反射率R＝0.98。）③如果用该F－P腔分辨谱线，其色分辨本领有多大？可分辨的最小波长间隔是多少？④如果用其对白光进行选频，透射最强的谱线有几条？每条谱线的宽度是多少？⑤由于热胀冷缩所引起的腔长的改变量为10－5（相对值），则谱线的漂移量是多少？

18.若用钠光灯的双谱线λ＝5.890×10－7 m和λ＝5.896×10－7 m照明Michelson干涉仪，首先调整干涉仪，得到清晰的干涉条纹，然后移动M1，干涉图样为什么会逐渐变得模糊？问第一次视场中干涉条纹消失时，M1移动了多少距离？

19.玻璃板上有一层油膜，波长可连续改变的单色光正入射，在λ＝6×10－7 m时，观察到反射光干涉相消，并且在这两波长之间再无其他波长的光相消。①证明油膜的折射率一定小于1.5（玻璃的折射率为1.5）。②若油的折射率为1.3，求油膜的厚度。

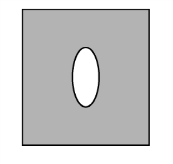
图3－16 习题20示意图

20.如图3－16所示，在一厚玻璃中有一气泡，形状类似球面透镜，用单色光从玻璃的左侧垂直入射。①说明在右侧看到的干涉条纹的特点，即形状、间距、级数和边界处的条纹特点。②若均匀用力挤压玻璃的左右两侧，条纹有何变化？

21.波长为λ的平行单色光以小倾角θ斜入射到间距为t的双缝上，设接收屏到双缝的距离为D。①求零级主极大的位置。②假设在屏上到双缝距离都相等的地方恰好出现暗条纹，倾角θ必须满足什么条件？

22.一台迈克尔逊干涉仪，使用波长λ＝550nm的扩展光源，调节两臂使干涉仪产生同心圆环干涉条纹。①此圆环干涉条纹为何种干涉条纹？②要使干涉圆环向中心一一消失20个圆环条纹，则可动臂必需移动多远？③空气平板是变厚还是变薄了？

23.如图3－17所示，点光源S发射的球面波与平面波满足相干条件，若在x0y0平面上两波具有相同的位相，在xy平面上两波具有相同的振幅，距S1m远的、与平面波传播方向垂直的xy平面满足x2＋y2≪1m，那么：①xy平面上的干涉条纹是什么形状？②干涉条纹的间距和空间频率各是多少？

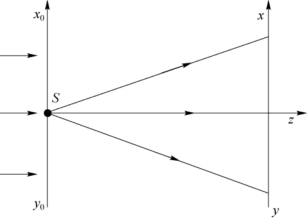
图3－17 习题23示意图

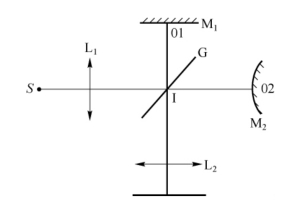
图3－18 习题24示意图

24.如图3－18所示，将一台泰曼－格林干涉仪的一个反射镜改为球面反射镜，使用波长为550nm的光源远心照明，调节球面反射镜的镜臂，使其产生同心圆环干涉条纹。①此圆环干涉条纹为何种干涉条纹？②要使干涉圆环向中心一一消失20个圆环条纹，则可动臂必需移动多远？③M2的移动方向是向左还是向右？

25.将一个波长稍小于600nm的光波与一个波长为600nm的光波在F－P干涉仪上进行比较，当F－P干涉仪的两镜面间距离改变2.0mm时，两光波的条纹系就重合一次（干涉条纹基本消失），试求未知光波的波长。

26.波长为λ、振幅为A、传播方向平行于xz平面但与z轴的夹角为θ的平面波，与光源位于z轴上，距坐标原点的距离为a，波长也为λ的球面波在z＝0平面发生干涉。设发散球面波在（0，0，－a）点与平面波在坐标原点的初相位相等，振幅也为A，a2≫x2＋y2，请问：①在z＝0平面上干涉条纹是什么形状？②干涉条纹的间距是多少？

27.波长为500nm的绿光投射在间距d为0.022cm的双缝上，在距离180cm处的光屏上形成干涉条纹，求两个亮条纹之间的距离。若改用波长为700nm的红光投射到此双缝上，两个亮条纹之间的距离又为多少？算出这两种光第2级亮纹的位置。

28.在杨氏实验装置中，光源的波长为640nm，两狭缝间距为0.4mm，光屏离狭缝的距离为50cm。试求：①光屏上第1亮条纹和中央亮条纹之间的距离；②若p点离中央亮条纹0.1mm，问两束光在p点的相位差是多少？③求p点的光强度和中央点的强度之比。

29.把折射率为1.5的玻璃片插入杨氏实验的一束光路中，光屏上原来第5级亮条纹所在的位置为中央亮条纹，试求插入的玻璃片的厚度，已知光的波长为6×10－7 m。

30.波长为500nm的单色平行光射在间距为0.2mm的双狭缝上，通过其中一个缝的能量为另一个的2倍，在离狭缝50cm的光屏上形成干涉图样，求干涉条纹间距和条纹的可见度。

31.波长为700nm的光源与菲涅耳双镜的相交棱之间的距离为20cm，棱到光屏间的距离L为180cm，若所得干涉条纹中相邻亮条纹的间隔为1mm，求双镜平面之间的夹角θ。

32.在如图3－19所示的劳埃德镜实验中，光源S到观察屏的距离为1.5m，到劳埃德镜面的垂直距离为2mm。劳埃德镜长40cm，置于光源和屏之间的中央。①若光波波长λ＝500nm，问条纹间距是多少？②确定屏上可以看见条纹的区域大小，此区域内共有几条条纹？（提示：产生干涉的区域P1P2可由图中的几何关系求得。）

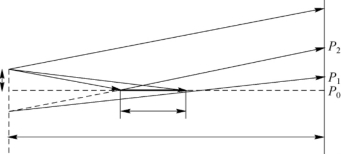
图3－19 劳埃德镜实验

33.迈克尔逊干涉仪的反射镜M2移动0.25mm时，看到条纹移过的数目为909个，设光为垂直入射，求所用光源的波长。

34.迈克尔逊干涉仪平面镜的面积为4×4cm2，观察到该镜上有20个条纹。当入射光的波长为589nm时，两镜面之间的夹角为多大？

35.调节一台迈克尔逊干涉仪，使其用波长为500nm的扩展光源照明时会出现同心圆环条纹。若要使圆环中心处相继出现1 000条圆环条纹，则可动臂将移动多远的距离？若中心是亮的，试计算第一暗环的角半径。（提示：圆环是等倾干涉图样。计算第一暗环角半径可利用θ≈sinθ及cosθ≈1－θ2／2的关系。）

36.用单色光观察牛顿环，测得某一亮环的直径为3mm，在它外边第5个亮环的直径为4.6mm，所用平凸透镜的凸面曲率半径为1.03m，求此单色光的波长。

37.在反射光中观察某单色光所形成的牛顿环。其第2级亮环与第3级亮环的间距为1mm，求第19和第20级亮环之间的距离。

38.菲涅耳双棱镜实验装置尺寸如图3－20所示：缝到棱镜的距离为5cm，棱镜到屏的距离为95cm，棱镜角为α＝179°32′，构成棱镜玻璃材料的折射率为n′＝1.5，采用的是单色光。当厚度均匀的肥皂膜横过双棱镜的一半部分放置时，该系统中心部分附近的条纹相对原先有0.8mm的位移。若肥皂膜的折射率为n＝1.35，试计算肥皂膜厚度的最小值。

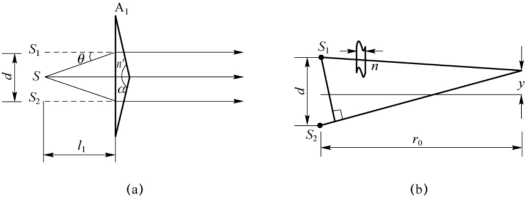
图3－20 菲涅耳双棱镜实验装置

39.将焦距为50cm的会聚透镜中央部分C切去（见图3－21），余下的A、B两部分仍旧粘起来，C的宽度为1cm。在对称轴线上距透镜25cm处置一点光源，发出波长为692nm的红宝石激光，在对称轴线上透镜的另一侧50cm处置一光屏，平面垂直于轴线。试求：①干涉条纹的间距是多少？②光屏上呈现的干涉图样是怎样的？

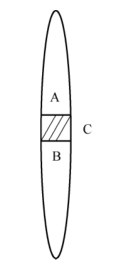
图3－21 习题39示意图