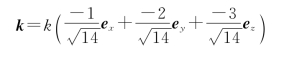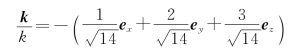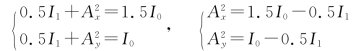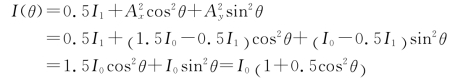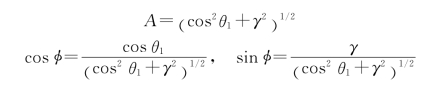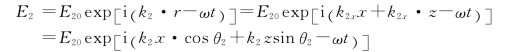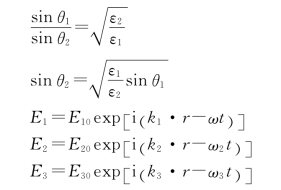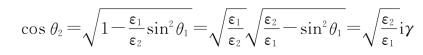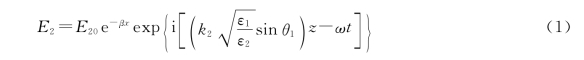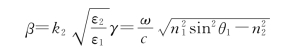2.4 习题解答
1.解:因为t是正的面而且在增大,所以要保持相位不变的状态即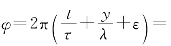 常数,要求y要减少。换句话说,由于φ是常数,Ψ1必然是沿负y方向运动的波。同样地,Ψ2是沿z增加的方向或z正方向运动的波。ε的符号同运动方向是无关的。
常数,要求y要减少。换句话说,由于φ是常数,Ψ1必然是沿负y方向运动的波。同样地,Ψ2是沿z增加的方向或z正方向运动的波。ε的符号同运动方向是无关的。
2.解:假设A点的初相位为零,因此插入薄片前B点的相位为
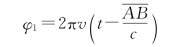
这里假设空气中光的传播速度为c。插入薄片后,光波在薄片内的传播速度为v,于是这时B点的相位为
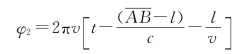
所以B点的相位为
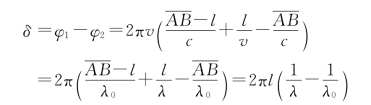
式中λ为光波在薄片内的波长。因为λ=λ0/n,所以上式又可写为
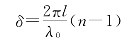
把l、n和λ0的数值代入,得到
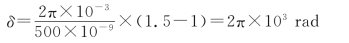
3.解:①如图2-17所示,设空气和平板玻璃的折射率分别为n1和n2,当光束从空气到玻璃的上表面以布儒斯特角i1B=arctan(n2/n1)入射时,折射光线在下表面从玻璃到空气的入射角(即折射角)i2=90°-i1B,故有
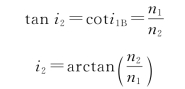
即下表面的入射角仍为布儒斯特角,光束以i1B入射到界面上时,恒有p分量的振幅反射率。由以上分析可知,把p方向的线偏振光以i1B从空气入射到平板玻璃上,并忽略介质对光的吸收,透射光即可获得全部入射光能流。取n1=1.52,n2=1.00,可算出入射布儒斯特角
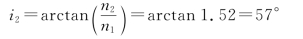
②以布儒斯特角i1B入射,只能使p分量满足,并不能使s分量的rs=100%。因此,即使以s振动的线偏振光在i1B入射,也不能实现透射能流为零。欲使透射能流为零,只有利用全反射,对于在空气中的平板玻璃,全反射只能发生在其下表面。当光线在下表面的入射角为临界角时,上表面相应的入射角为90°,所以只有令光束掠入射到玻璃板上,才能实现透射能流为零,当然,此时对入射光束的偏振态并无限制。
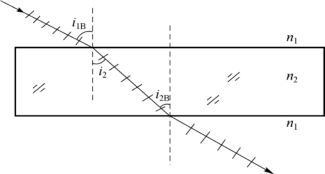
图2-17 光束经过平行玻璃板光路示意图
4.解:①在光束正入射或入射角很小的情况下,cosθ1≈cosθ2≈1。因此
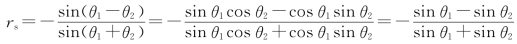
以sinθ2除分子和分母,并注意到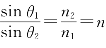 (相对折射率),得到
(相对折射率),得到
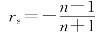
②在角度很小时,tanθ≈sinθ,故
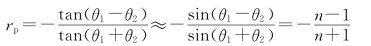
③
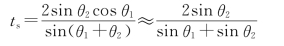
以sinθ2除分子和分母,得到
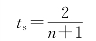
④
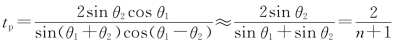
由此可见,当光束正入射或入射角很小时,s波和p波的差别将消失。原因在于:s波和p波的规定源于相对于光束的入射面的垂直或平行分量,当光束正入射时,入射面将不唯一,s波和p波将无差别。
5.解:根据公式有
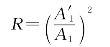
由于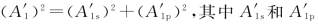 为反射光中s波和p波的振幅,所以
为反射光中s波和p波的振幅,所以
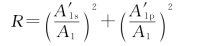
对于入射光,s波和p波的振幅分别为
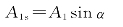
和
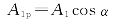
因此
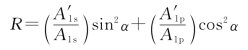
或者写为
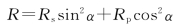
同样,可以证明总透射率T有这样的形式
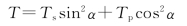
6.解:系统包括4个分界面,假设光束在接近正入射情形下通过各反射面,因而各面的反射率分别为
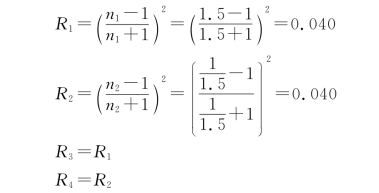
如果入射到系统的光能为W,则相继透过各面的光能为
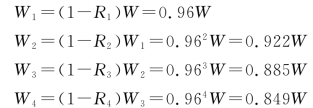
光能损失
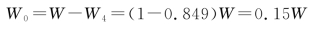
故光能损失为15%。
7.解:在接近正入射的情况下,光束从空气-平板界面反射的反射率为
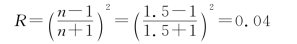
显然,光束从平板-空气界面反射的反射率也等于R。设入射光束的强度为I,则第1条反射光束的强度为
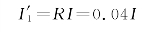
第2条反射光束的强度为
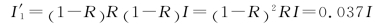
头两条透射光束的强度分别为
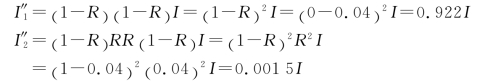
可以看出,头两条反射光束的强度比较接近,而头两条透射光束的强度相差很大。
8.解:①为了保证光线在光纤内的入射角大于临界角,必须使入射到光纤端面的光线限制在最大孔径角2u的范围内。在光纤端面应用折射定律
sin u=n1sin (90°-θc)=n1cosθc
而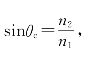 因此
因此
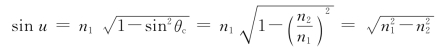
②当n1=1.62,n2=1.52时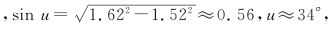 所以最大孔径角2u=68°。
所以最大孔径角2u=68°。
9.解:①E1分解成水平方向的分量E1x和垂直分量E1y,E1x与E2的频率相同,传播方向相反,相互叠加形成驻波Ex,E1y为沿z轴传播的行波,合成波为x方向的驻波和y方向的行波。

10.解:①F-P干涉仪和衍射光栅。
②群速是等幅度面传播的速度。相速是光波等相位面传播的速度。在正常色散介质中,群速慢于相速。在反常色散介质中,相速慢于群速。
11.解:由
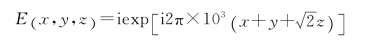
可得
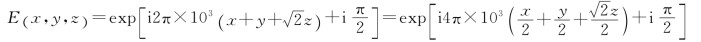
则可知φ0=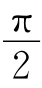 rad,k0=4π×103,而k0=
rad,k0=4π×103,而k0=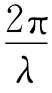 =4π×103,因此λ=5×10-2 m,则k0的方向为
=4π×103,因此λ=5×10-2 m,则k0的方向为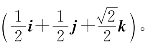
12.解:假定光波的初相位为0,则一般的波函数为
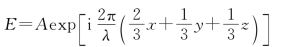
在xOy平面上的复振幅为
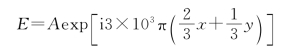
13.解:
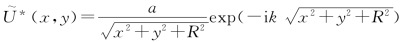
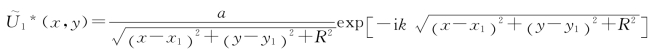
它们都是会聚的球面波,会聚中心O*和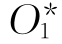 分别与O和O1对波前成镜像对称。
分别与O和O1对波前成镜像对称。
14.解:①一般的波函数可以写成以下形式
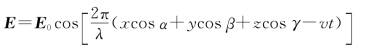
类比可知波长为600nm,频率为5×1014 Hz。
②传播方向:在xOz坐标平面内,与x轴夹角为135°,与z轴夹角为45°。偏振方向:在xOy坐标平面内,与x轴、y轴的夹角均为45°。
③波长为400nm,频率不变,为5×1014 Hz。
玻璃中传播方向:与x轴的夹角为62°,与z轴的夹角为152°。
透射光:垂直分量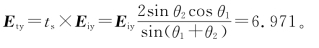
平行分量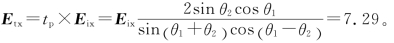
偏振矢量与入射面的夹角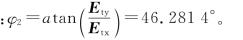
15.证明:设入射光波的波函数

反射光波的波函数

折射光波的波函数

由边界条件可得

把式(1)、式(2)、式(3)代入式(4)可得
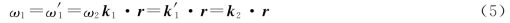
由式(5)可得
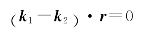
又因为
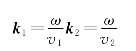
也即
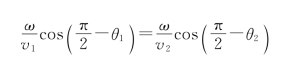
故
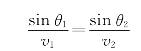
因此
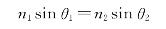
得证。
16.解:如图2-18所示,该平面波波失的3个分量分别为
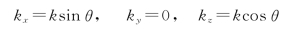
其复振幅为
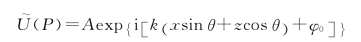
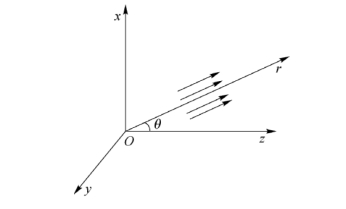
图2-18 平面波波矢在坐标系中的表示图
17.解:如图2-19所示,设源点为Q(x0,y0,z0),场点为P(x,y,z),则源点与场点的距离为
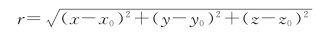
因为Q点是会聚中心,所以沿靠近点源方向考查,扰动相位逐点落后,按符号约定应写成
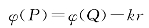
再考虑振幅系数,这列球面波的复振幅为
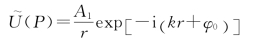
其中φ0为Q点源的实际初相位。
18.解:①设自然光(即入射光)的总强度为I0,通过第一块偏振片P1的强度为I0/2。当两块偏振片平行时,最后通过第二块偏振片P2的强度为I0/2,此为最大透光强度
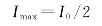
当P1、P2的透振方向夹角为θ(如图2-20所示)时,则
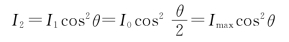
若I2/Imax=1/3,算出 故
故
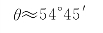
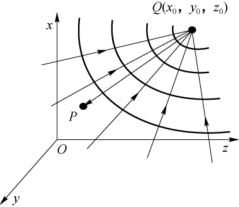
图2-19 源点Q坐标系表示图
②若I2/I0=1/3,算出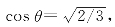 故
故
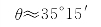
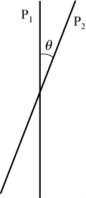
图2-20 P1、P2的透振方向夹角为θ
19.解:设偏振片P1、P2正交,则最终通过P2的光强为
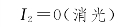
若在P1、P2之间插入另一块偏振片P,P与P1的夹角为θ(如图2-21所示),则最终通过P2的光强为
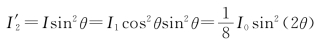
式中I0为入射光强,I1、I分别为通过P1、P后的光强。当θ=45°时
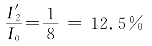
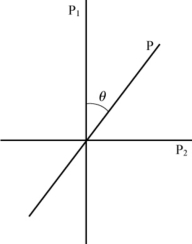
图2-21 P与P1的夹角为θ
20.解:因该偏振光以布儒斯特角入射,反射光显然为s光,即反射光的方位角α′1=90°,在上题结果中取i=iB,taniB=n2/n1,进一步简化折射线偏振方位角公式
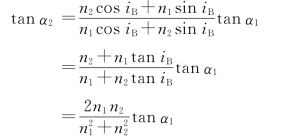
将n1=1,n2=1.560,α1=20°代入,算得
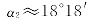
21.解:①将n1=1.51,n2=1.0,i1=54°37′代入公式中,分别算出
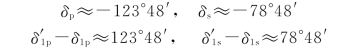
②考查全反射光中s振动和p振动的实际相位差。设入射光为线偏振光,且δ1s-δ1p=0,则
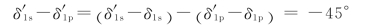
两个振动合成结果为左旋的椭圆偏振光,如图2-22所示。
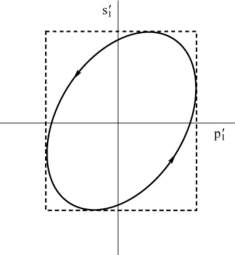
图2-22 两个振动合成结果示意图
22.解:矢量图给出了自然光中大量横振动的方位分布。它表明自然光是大量相对于光的传播方向轴对称分布的线偏振光的集合。与矢量图解法中的振幅矢量不同,目前各矢量间的夹角并不代表各振动间的相位差,因此不能对它们进行合成。由于自然光中各方向横振动之间的相位是无关联的,所以总的光强是所有各方向横振动的线偏振光的非相干叠加,显然不为零。
23.解:自然光和圆偏振光都可看成是两个等幅垂直偏振的合成。它们的主要区别在于前者光振动矢量的两个正交分量之间没有稳定的相位关系;而后者的两个正交分量之间有确定的相位差±π/2。部分偏振光和椭圆偏振光的主要区别也在相位关系上:前者两正交分量之间无稳定的相位关系;后者两个正交分量之间有稳定的相位差。在确定两个垂直偏振合成后的偏振态时,起决定作用的是两者的相位关系及其振幅关系。
24.解:粗略地判定偏振片的透振方向,一种简单的方法是根据反射光的偏振性判定。如图2-23所示,自然光从空气到玻璃入射,并使入射角为布儒斯特角iB(约57°),则反射偏振光的振动方向是垂直入射面的。旋转偏振片并观察反射光,可得消光位置。消光时,偏振片上与入射面平行的方向即为透振方向。当然,实验时来自普通光源的入射光并不一定是平行光,入射角也不必严格校准。这时“消光”并不精准,但强度最小的位置还是可以非常明显地观察到的。例如,隔着偏振片观察物体以接近入射经玻璃反射的像,旋转偏振片,可观察到像的亮度变化。当观察到像的亮度最小时,偏振片上与入射面平行的方向就是透振方向。
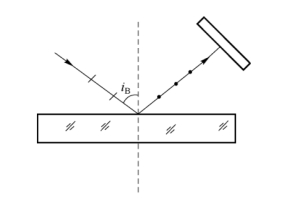
图2-23 自然光从空气到玻璃的反射示意图
25.解:①当θ1=50°时,由折射定律
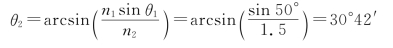
因此
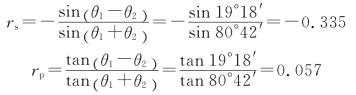
因为入射光中电矢量振动方向与入射面成45°,故在入射光中,电矢量垂直于入射面分量E1s的振幅A1s等于平行于入射面分量E1p的振幅A1p。但在反射光中,由于rs≠rp,所以反射光中电矢量两个分量的振幅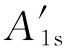 和
和 不相等,它们的数值分别为
不相等,它们的数值分别为
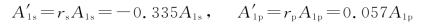
rs的负值表示 的方向与E1s的方向相反。因此,反射光中电矢量两个分量的合振幅与入射面的夹角α由下式决定
的方向与E1s的方向相反。因此,反射光中电矢量两个分量的合振幅与入射面的夹角α由下式决定
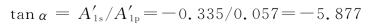
得到α=-80°20′。
②当θ1=60°时,有
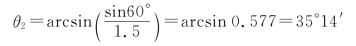
故
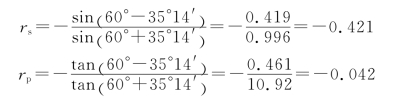
因此,反射光电矢量的振动方向与入射面所成的夹角为
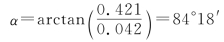
26.解:由于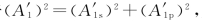 所以,据公式有
所以,据公式有
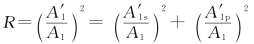
对于入射光,s波和p波的振幅分别为A1s=A1sinα,A1p=A1cosα。因此
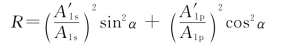
或者写为R=Rssin2α+Rpcos2α。
类似的做法可以证明总透射率T有这样的形式:
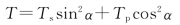
27.解:对于选定的几个不同时刻,合成电矢量为
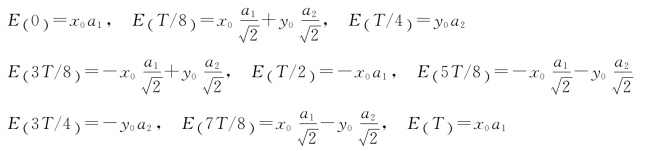
如图2-24所示,它们的端点分别对应于图中的点A、B、C、D、E、F、G、H、A。可见,随着t的增大,合成电矢量的端点做左旋运动。若选取更小的时间间隔,可得到合成电矢量端点的运动轨迹为一椭圆。
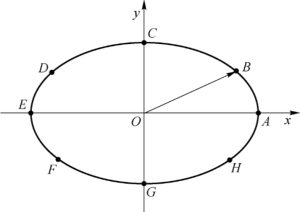
图2-24 不同时刻场矢量端点的位置
事实上,由于δ=π/2,所以合成电矢量端点的运动方程为
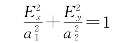
这是一个长短轴2a1、2a2和坐标轴x、y重合的椭圆,即如图2-24所示的标准椭圆。
28.解:①要使菱体的出射光为圆偏振光,出射光的p波和s波的振幅必须相等(入射线偏振光的电矢量与图面成45°保证了这一条件的实现),位相差必须等于π/2。光束在菱体内以相同条件全反射两次,每次全反射后p波和s波的位相差必须等于π/4。全反射条件下p波和s波的位相差的计算公式为
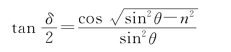
已知n=1/1.5,为使δ=π/4,由上式可解出光束在菱体内的入射角,上式两边平方,得到
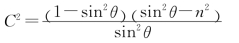
式中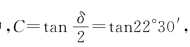 整理后得到
整理后得到
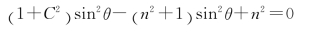
把C和n的值代入,得到方程的解:θ=53°15′或θ=50°13′。由于φ=θ,所以菱体顶角可选53°15′或50°13′。
②对于一定的菱体折射率n,位相差δ有一极大值,它由下式决定
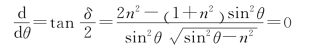
其解为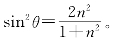 把这一结果代入δ的计算公式,得到位相差极大值δm的表示式为
把这一结果代入δ的计算公式,得到位相差极大值δm的表示式为
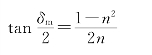
当n=1/1.49时,tan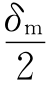 =0.409 4,δm=44°32′,所以δm<π/4。因此光束在菱体内两次全反射后不能产生圆偏振光。
=0.409 4,δm=44°32′,所以δm<π/4。因此光束在菱体内两次全反射后不能产生圆偏振光。
29.解:由平面波的相位特性

波矢为
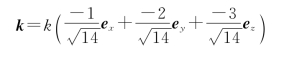
方向为
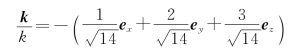
30.解:椭圆的长轴沿x方向。设自然光的光强为I1,而椭圆偏振光分量的振幅为Ax、Ay。则
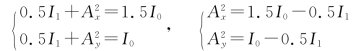
P与x轴成θ角,考虑椭圆偏振光的两正交分量间的相位差为π/2,所以透射光强
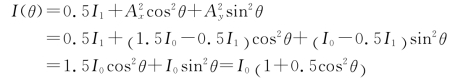
可见,透射光强与入射光中无偏振部分(即自然光)的光强I1无关。
31.解:此题考查的是矢平面电磁波的表达式以及其各个参数之间的关系。
①根据平面电磁波的通用表达式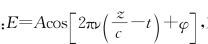 对应有ω=2πν=2π×1014 rad/s,即频率ν=1014 Hz
对应有ω=2πν=2π×1014 rad/s,即频率ν=1014 Hz 当z=0,t=0时初相位
当z=0,t=0时初相位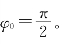
②由表达式可知,波沿z轴正方向传播,电矢量振动方向为y轴。
③B与E垂直,传播方向相同,因为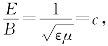 所以相应磁场B的表达式为
所以相应磁场B的表达式为
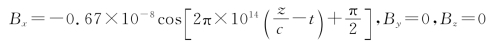
32.解:本题考查的是平面简谐电磁波的表达式,以及其各参数的关系和性质。
电矢量的振幅在x和y方向上的分量分别为
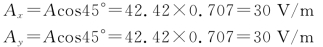
因此该电矢量的表达式为
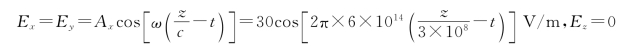
又
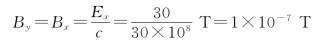
磁场的表达式为
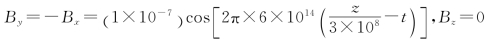
33.解:
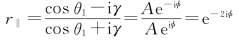
式中
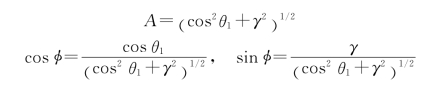
因此
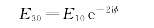
相变(Δ)为

34.解:与透射波相关的电场由下式给出
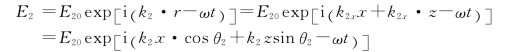
又有
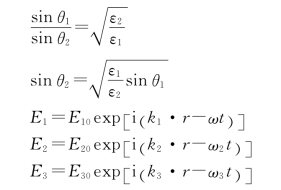
而
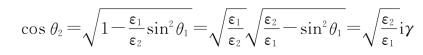
因此,有
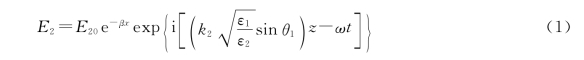
式中
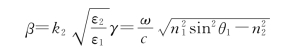
式(1)给出的场表示一个沿z方向传播,但振幅在x方向按照指数规律衰减的波,这种波称为“表面波”或“隐失波”。
35.解:区别方法如下。
①用一块偏振片分别垂直插入5种入射光,并以入射光线为轴,旋转偏振片一周,在透射光中观察光强变化:a.若光强没有变化,那么入射光是圆偏振光或自然光;b.若光强有变化,但是没有消光现象,那么入射光可能是椭圆偏振光或者部分偏振光;c.若光强发生变化,且有消光现象,那么入射光必定是偏振光。
②进一步区分圆偏振光和自然光,椭圆偏振光和部分偏振光采用在该偏振片之前,再平行插入一块1/4波晶片的方法。对于自然光和部分偏振光在通过1/4波晶片之后,虽然发生双折射,但是两种光无固定的相位差,因此通过偏振片之后光强变化情况与前者无异。而对于圆偏振光和椭圆偏振光来说,通过波晶片后,相位差再增加π/2,通过晶片会合成偏振光,此时再透过偏振片就会看到消光现象。
至此5种光均可区分开来。
36.解:①E1=Acos(k·xsinθ+k·zcosθ-ωt),E2=Acos[k·xsin(-θ)+k·zcosθ-ωt]。
②E1=Aexp [i k (xsinθ+zcosθ)],E2=Aexp {i k [x(-sinθ)+zcosθ]}。
③U(x,y)=Aexp (i kxsinθ)+Aexp [i kxsin(-θ)]=2cos (kxsinθ)。
④分布图如图2-25所示,当kxsinθ等于2π的整数倍时,U(x,y)=1;当kxsinθ等于π的奇数倍时,U(x,y)=-1;当kxsinθ等于π/2的奇数倍时,U(x,y)=0。
空间频率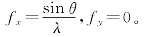
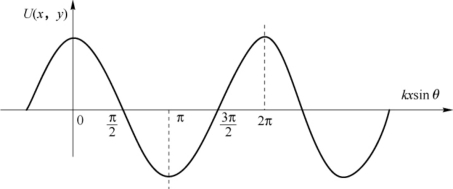
图2-25 U(x,y)的分布图
⑤I(x,y)=4cos2 (kxsinθ)=2+2cos (2kxsinθ)。
⑥如图2-26所示,当kxsinθ等于π的整数倍时,I (x,y)=4;当kxsinθ等于π/2的奇数倍时,I (x,y)=0;当kxsinθ等于π/4的奇数倍时,I (x,y)=2。
空间频率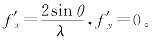
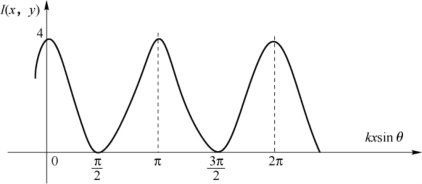
图2-26 I(x,y)的分布图
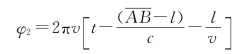
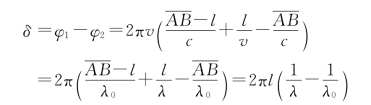
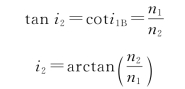

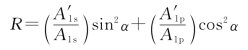
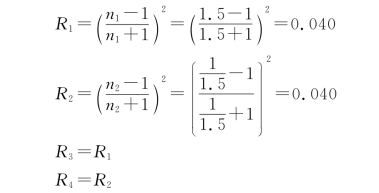
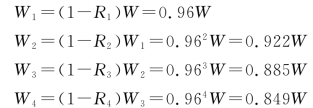
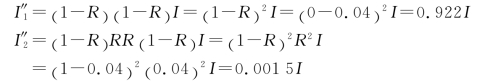
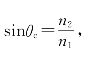 因此
因此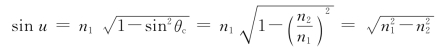

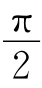 rad,k
rad,k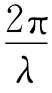 =4π×10
=4π×10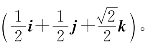
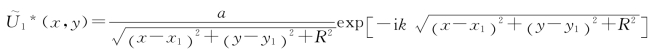
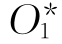 分别与O和O
分别与O和O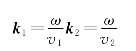
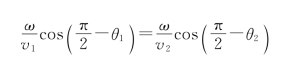
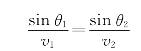




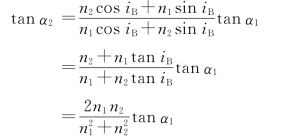
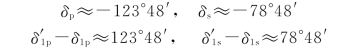


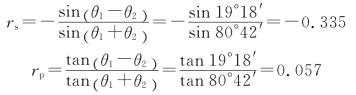
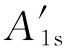 和
和 不相等,它们的数值分别为
不相等,它们的数值分别为 的方向与E
的方向与E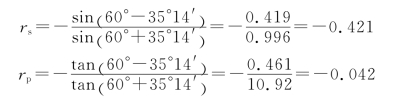
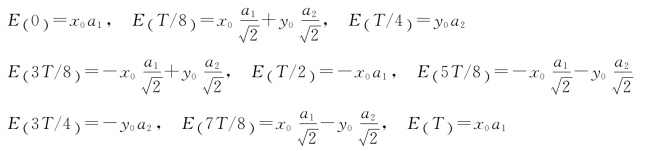

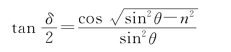
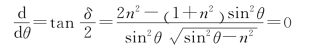
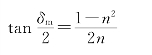
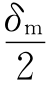 =0.409 4,δ
=0.409 4,δ