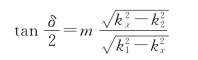-
1.1内容简介
-
1.2前 言
-
1.3第1章 几何光学基础
-
1.3.11.1 知识要点
-
1.3.21.2 典型例题
-
1.3.31.3 习 题
-
1.3.41.4 习题解答
-
1.4第2章 光波的描述
-
1.4.12.1 知识要点
-
1.4.22.2 典型例题
-
1.4.32.3 习 题
-
1.4.42.4 习题解答
-
1.5第3章 光的干涉
-
1.5.13.1 知识要点
-
1.5.23.2 典型例题
-
1.5.33.3 习 题
-
1.5.43.4 习题解答
-
1.6第4章 光的衍射
-
1.6.14.1 知识要点
-
1.6.24.2 典型例题
-
1.6.34.3 习 题
-
1.6.44.4 习题解答
-
1.7第5章 光栅光谱
-
1.7.15.1 知识要点
-
1.7.25.2 典型例题
-
1.7.35.3 习 题
-
1.7.45.4 习题解答
-
1.8第6章 傅里叶变换光学
-
1.8.16.1 知识要点
-
1.8.26.2 典型例题
-
1.8.36.3 习 题
-
1.8.46.4 习题解答
-
1.9第7章 光在晶体中的传播
-
1.9.17.1 知识要点
-
1.9.27.2 典型例题
-
1.9.37.3 习 题
-
1.9.47.4 习题解答
-
1.10第8章 光波与物质的相互作用
-
1.10.18.1 知识要点
-
1.10.28.2 典型例题
-
1.10.38.3 习 题
-
1.10.48.4 习题解答
-
1.11第9章 光的量子性
-
1.11.19.1 知识要点
-
1.11.29.2 典型例题
-
1.11.39.3 习 题
-
1.11.49.4 习题解答
1
大学物理光学学习指导书
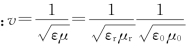 (ε
(ε
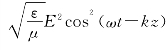 为瞬时迅变值,实际测得的光强为时间平均值:
为瞬时迅变值,实际测得的光强为时间平均值:
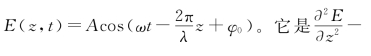
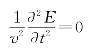 。的解
。的解 为时间频率,f=
为时间频率,f=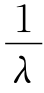 为空间频率,可以表示为:
为空间频率,可以表示为:
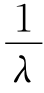 ,空间圆频率k=
,空间圆频率k=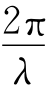 ,f=
,f=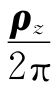 ,故空间频率与观察方向有关。
,故空间频率与观察方向有关。 值时的半径)
值时的半径)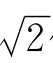 倍(光斑面积增大两倍)时的范围。
倍(光斑面积增大两倍)时的范围。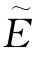 (p)可以表示振幅分布和相位分布。
(p)可以表示振幅分布和相位分布。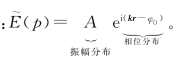
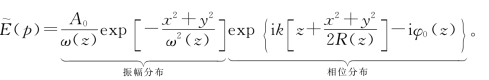
 故可忽略该因子。
故可忽略该因子。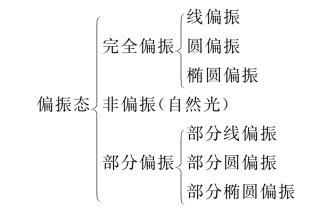
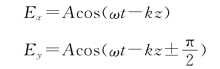
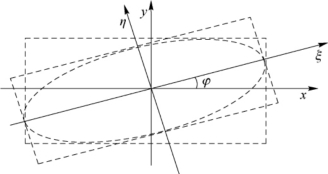
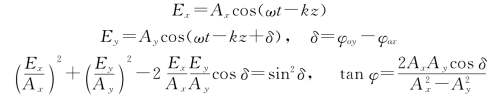
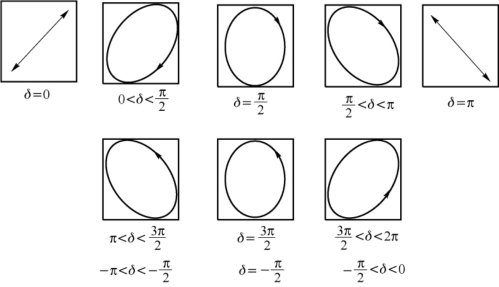
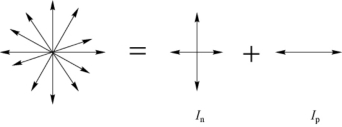

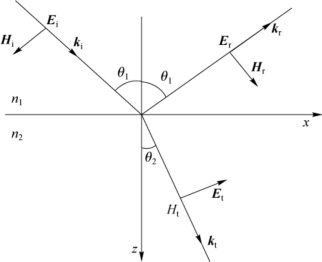
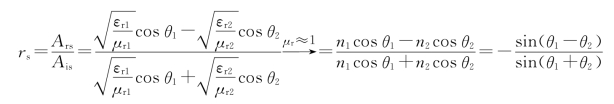
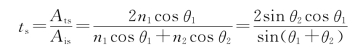
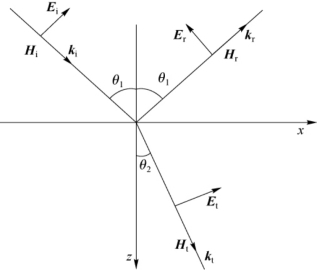
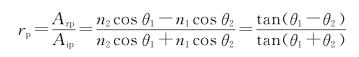
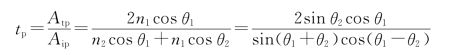
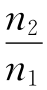 。
。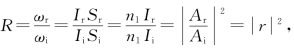 透射率
透射率 可证R+T=1,即代表能量守恒。
可证R+T=1,即代表能量守恒。
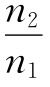 。
。