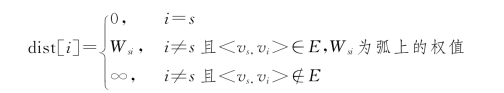算法与数据结构 C语言版
-
1.1内容简介
-
1.2前 言
-
1.3第1章 数据结构与算法
-
1.3.11.1 学习数据结构
-
1.3.1.11.1.1 为什么学习数据结构
-
1.3.1.21.1.2 如何学习数据结构
-
1.3.21.2 基本概念和术语
-
1.3.2.11.2.1 基本概念
-
1.3.2.21.2.2 逻辑结构和存储结构
-
1.3.31.3 算 法
-
1.3.3.11.3.1 算法的定义
-
1.3.3.21.3.2 算法的特性
-
1.3.3.31.3.3 算法效率度量方法
-
1.3.3.41.3.4 算法的时间复杂度
-
1.3.4本章小结
-
1.3.5练习题
-
1.4第2章 线性表
-
1.4.12.1 线性表及其逻辑结构
-
1.4.1.12.1.1 线性表的定义
-
1.4.1.22.1.2 线性表的基本运算
-
1.4.22.2 线性表的顺序存储结构
-
1.4.2.12.2.1 线性表的顺序存储结构——顺序表
-
1.4.2.22.2.2 顺序表基本运算的实现
-
1.4.32.3 线性表的链式存储结构
-
1.4.3.12.3.1 线性表的链式存储结构——链表
-
1.4.3.22.3.2 单链表
-
1.4.3.32.3.3 循环链表
-
1.4.3.42.3.4 双链表
-
1.4.42.4 线性表的应用
-
1.4.52.5 顺序表和单链表的比较
-
1.4.6本章小结
-
1.4.7练习题
-
1.5第3章 栈和队列
-
1.5.13.1 栈
-
1.5.1.13.1.1 栈的定义及基本运算
-
1.5.1.23.1.2 栈的顺序存储结构及其基本运算实现
-
1.5.1.33.1.3 栈的链式存储结构及其基本运算的实现
-
1.5.23.2 栈的应用实例
-
1.5.2.13.2.1 数制转换问题
-
1.5.2.23.2.2 迷宫的求解
-
1.5.2.33.2.3 表达式求值
-
1.5.2.43.2.4 栈与递归
-
1.5.33.3 队 列
-
1.5.3.13.3.1 队列的定义及基本运算
-
1.5.3.23.3.2 队列的顺序存储结构及其基本运算的实现
-
1.5.3.33.3.3 队列的链式存储结构及其基本运算的实现
-
1.5.4本章小结
-
1.5.5练习题
-
1.6第4章 串
-
1.6.14.1 串的基本概念
-
1.6.1.14.1.1 串的基本概念
-
1.6.1.24.1.2 串的抽象数据类型
-
1.6.24.2 串的存储结构
-
1.6.2.14.2.1 串的顺序存储结构——顺序串
-
1.6.2.24.2.2 串的链式存储结构——链串
-
1.6.34.3 串的模式匹配
-
1.6.3.14.3.1 Brute-Force算法
-
1.6.3.24.3.2 KMP算法
-
1.6.4本章小结
-
1.6.5练习题
-
1.7第5章 数 组
-
1.7.15.1 数 组
-
1.7.1.15.1.1 数组的基本概念
-
1.7.1.25.1.2 数组的顺序表示和实现
-
1.7.25.2 特殊矩阵的压缩存储
-
1.7.2.15.2.1 特殊矩阵
-
1.7.2.25.2.2 稀疏矩阵
-
1.7.3本章小结
-
1.7.4练习题
-
1.8第6章 树和二叉树
-
1.8.16.1 树的定义和基本术语
-
1.8.26.2 二叉树
-
1.8.2.16.2.1 二叉树的概念
-
1.8.2.26.2.2 二叉树的性质
-
1.8.2.36.2.3 二叉树的存储
-
1.8.2.46.2.4 二叉树的基本操作及实现
-
1.8.36.3 二叉树的遍历
-
1.8.3.16.3.1 二叉树的遍历方法及递归实现
-
1.8.3.26.3.2 二叉树遍历的非递归实现
-
1.8.3.36.3.3 由遍历序列恢复二叉树
-
1.8.3.46.3.4 不用栈的二叉树遍历的非递归方法
-
1.8.46.4 线索二叉树
-
1.8.4.16.4.1 线索二叉树的定义及结构
-
1.8.4.26.4.2 线索二叉树的基本操作实现
-
1.8.4.36.4.3 树、森林与二叉树的转换
-
1.8.56.5 哈夫曼树及其应用
-
1.8.5.16.5.1 二叉树遍历的应用
-
1.8.5.26.5.2 最优二叉树——哈夫曼树
-
1.8.6本章小结
-
1.8.7练习题
-
1.9第7章 图
-
1.9.17.1 图的定义与基本术语
-
1.9.1.17.1.1 图的定义
-
1.9.1.27.1.2 基本术语
-
1.9.27.2 图的存储结构
-
1.9.2.17.2.1 邻接矩阵表示法
-
1.9.2.27.2.2 邻接表
-
1.9.2.37.2.3 十字链表
-
1.9.37.3 图的遍历
-
1.9.3.17.3.1 深度优先遍历
-
1.9.3.27.3.2 广度优先遍历
-
1.9.47.4 最小生成树
-
1.9.4.17.4.1 普利姆算法
-
1.9.4.27.4.2 克鲁斯卡尔算法
-
1.9.57.5 拓扑排序
-
1.9.5.17.5.1 拓扑排序
-
1.9.5.27.5.2 拓扑排序算法
-
1.9.67.6 关键路径
-
1.9.6.17.6.1 关键路径的概念和原理
-
1.9.6.27.6.2 关键路径算法
-
1.9.77.7 最短路径
-
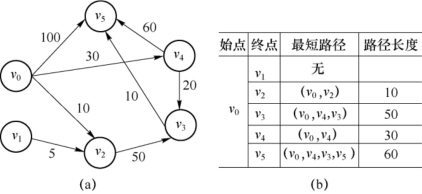
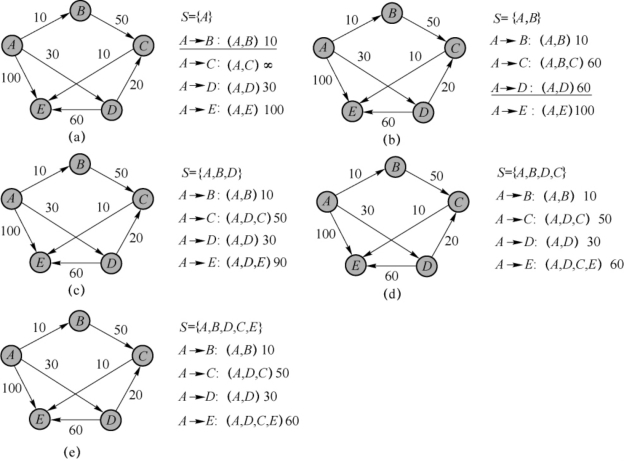
1.9.7.17.7.1 求某一顶点到其他各顶点的最短路径
-
1.9.7.27.7.2 求任意一对顶点间的最短路径
-
1.9.8本章小结
-
1.9.9练习题
-
1.10第8章 内部排序
-
1.10.18.1 基本概念
-
1.10.28.2 插入排序
-
1.10.2.18.2.1 直接插入排序
-
1.10.2.28.2.2 希尔排序
-
1.10.38.3 交换排序
-
1.10.3.18.3.1 冒泡排序
-
1.10.3.28.3.2 快速排序
-
1.10.48.4 选择排序
-
1.10.4.18.4.1 简单选择排序
-
1.10.4.28.4.2 堆排序
-
1.10.58.5 归并排序
-
1.10.5.18.5.1 2-路归并排序
-
1.10.5.28.5.2 2-路归并排序的时间复杂度
-
1.10.68.6 内部排序方法的比较和选择
-
1.10.7本章小结
-
1.10.8练习题
-
1.11第9章 查 找
-
1.11.19.1 查找基本概念
-
1.11.29.2 静态查找
-
1.11.2.19.2.1 顺序查找
-
1.11.2.29.2.2 二分查找
-
1.11.2.39.2.3 索引查找
-
1.11.39.3 动态查找
-
1.11.3.19.3.1 二叉排序树
-
1.11.3.29.3.2 平衡二叉树
-
1.11.49.4 散列表查找
-
1.11.4.19.4.1 散列表
-
1.11.4.29.4.2 散列函数构造方法
-
1.11.4.39.4.3 处理冲突的方法
-
1.11.4.49.4.4 散列表的查找和分析
-
1.11.5本章小结
-
1.11.6练习题
-
1.12参考文献