高等数学研究点滴
-
1.1内容简介
-
1.2前 言
-
1.3目录
-
1.4第一章 极限求法的研究
-
1.4.11.1 三个极限公式及应用
-
1.4.1.11.1.1 基本定理及其证明
-
1.4.1.21.1.2 应用举例
-
1.4.21.2 无穷小量部分代换求极限
-
1.4.2.11.2.1 基本定理(证明)及推论
-
1.4.2.21.2.2 应用举例
-
1.4.31.3 用带Peano余项的Taylor公式代换求极限应取的项数
-
1.4.3.11.3.1 基本定理(证明)及推论
-
1.4.3.21.3.2 应用举例
-
1.4.41.4 形如的限求法
-
1.4.4.11.4.1 Cauchy判别法和D’Alembert判别法及有关的结论
-
1.4.4.21.4.2 应用举例
-
1.4.51.5 用球面坐标求多元函数极限
-
1.4.5.11.5.1 定理(证明)及推论
-
1.4.5.21.5.2 应用举例
-
1.5第二章 微积分的研究
-
1.5.12.1 Taylor公式中的Lagrange型余项R(x)的研究
-
1.5.1.12.1.1 问题的提出
-
1.5.1.22.1.2 基本定理(证明)及推论
-
1.5.22.2 无穷小量之比单调性判别法及应用
-
1.5.2.12.2.1 基本定理及证明
-
1.5.2.22.2.2 应用举例
-
1.5.32.3 微分中值定理与Newton-Leibniz公式互相证明
-
1.5.3.12.3.1 用微分中值定理推出牛顿-莱布尼茨(Newton-Leibniz)公式
-
1.5.3.22.3.2 用Newton-Leibniz公式推出微分中值定理
-
1.5.42.4 微积分第一基本定理和积分中值定理的证法
-
1.5.4.12.4.1 用Newton-Leibniz公式证明微积分第一基本定理
-
1.5.4.22.4.2 用Lagrange中值定理证明积分中值定理
-
1.5.52.5 微分中值定理与Newton-Leibniz公式的证明体系
-
1.5.5.12.5.1 三个证明体系概述
-
1.5.5.22.5.2 两个证明体系的介绍
-
1.5.62.6 无穷积分收敛条件的探讨
-
1.5.6.12.6.1 问题的猜想
-
1.5.6.22.6.2 基本定理(证明)及推论
-
1.5.6.32.6.3 应用举例
-
1.5.72.7 形如的无穷积分敛散性
-
1.5.7.12.7.1 定理及证明
-
1.5.7.22.7.2 应用举例
-
1.5.82.8 反常积分敛散性审敛法的等价定理
-
1.5.8.12.8.1 审敛法的等价定理及其证明
-
1.5.8.22.8.2 应用举例
-
1.5.92.9 Stokes公式的二重积分形式及应用
-
1.5.9.12.9.1 基本定理及证明
-
1.5.9.22.9.2 应用举例
-
1.5.102.10 用亚纯函数的留数计算曲线(实)积分
-
1.5.10.12.10.1 基本定理(证明)及推论
-
1.5.10.22.10.2 应用举例
-
1.6第三章 级数审敛法的等价定理研究
-
1.6.13.1 正项级数审敛法的等价定理及其证明
-
1.6.1.13.1.1 等价定理及证明
-
1.6.1.23.1.2 应用举例
-
1.6.23.2 魏尔斯特拉斯(Weierstrass)判别法的等价定理
-
1.6.2.13.2.1 等价定理及其证明
-
1.6.2.23.2.2 应用举例
-
1.7第四章 空间解析几何的研究
-
1.7.14.1 空间几何体在平面上的投影
-
1.7.1.14.1.1 基本定理(证明)及推论
-
1.7.1.24.1.2 应用举例
-
1.7.24.2 空间曲线在平面上的投影曲线参数方程
-
1.7.2.14.2.1 基本定理及证明
-
1.7.2.24.2.2 应用举例
-
1.7.34.3 旋转曲面方程的求法
-
1.7.3.14.3.1 基本定理(证明)及推论
-
1.7.3.24.3.2 应用举例
-
1.7.44.4 旋转曲面的面积及围成立体的体积
-
1.7.4.14.4.1 基本定理(证明)及推论
-
1.7.4.24.4.2 应用举例
-
1.8参考文献
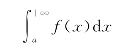 收敛;
收敛;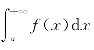 发散.
发散. 收敛,由比较准则知
收敛,由比较准则知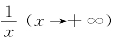 的同阶或低阶无穷小,则一定存在常数N>0,使
的同阶或低阶无穷小,则一定存在常数N>0,使 发散,故由比较准则知
发散,故由比较准则知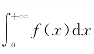 也发散.
也发散.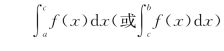 发散.
发散.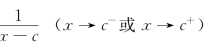 的同阶或高阶无穷大,则一定存在常数N>0,使
的同阶或高阶无穷大,则一定存在常数N>0,使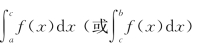 发散.
发散.