-
1.1内容提要
-
1.2前 言
-
1.3目录
-
1.4绪 言
-
1.4.1一、物理化学的目的和内容
-
1.4.2二、物理化学的研究方法
-
1.4.3三、物理化学的形成、发展和展望
-
1.4.3.11.物理化学的形成
-
1.4.3.22.物理化学的发展和展望
-
1.4.4四、物理化学的学习方法
-
1.5第一章 准备知识(Preparation knowledge)
-
1.5.1第一节 化学计量与有效数字(Stoichiometry and Significant Figure...
-
1.5.1.1一、SI单位制(SI System of Unit)
-
1.5.1.2二、有效数字及其运算(Significant Figure and Operation)
-
1.5.2第二节 理想气体(Ideal Gases)
-
1.5.2.1一、气体的基本实验定律(Basic Experimental Laws of Gases)
-
1.5.2.2二、理想气体及其状态方程(Ideal Gases and Equation of State)
-
1.5.3第三节 理想气体混合物(Mixtures of Ideal Gases)
-
1.5.3.1一、道尔顿分压定律(Dalton Partial Pressure Law)
-
1.5.3.2二、阿马格分体积定律(Amagat Partial Volume Law)
-
1.5.4第四节 实际气体的状态方程(Equations of States of Real Gases)
-
1.5.4.1一、实际气体对理想气体的偏差(Deviations of Real Gases from Ideal...
-
1.5.4.2二、范德华方程式(Van der Waals Equation)
-
1.5.4.3三、维里方程(Virial Equation)
-
1.5.5第五节 实际气体的液化与临界状态(Liquefaction and Critical State o...
-
1.5.6第六节 对应状态原理和压缩因子图(Principle of Corresponding State ...
-
1.5.6.1一、对应状态原理(Principle of Corresponding State)
-
1.5.6.2二、普遍化压缩因子图(Universal Compressibility Factor Diagra...
-
1.6第二章 热力学基础(Thermodynamic BaSiS)
-
1.6.1第一节 热力学基本概念和术语(The Fundamental Concepts and Termin...
-
1.6.1.1一、系统和环境(System and Surroundings)
-
1.6.1.2二、系统的热力学性质(Thermodynamic Property of System)
-
1.6.1.3三、系统的状态和状态函数(State and State Function of System)
-
1.6.1.4四、过程和途径(Process and Path)
-
1.6.1.5五、热力学平衡态(Thermodynamic Equilibrium State)
-
1.6.2第二节 热和功(Heat and Work)
-
1.6.2.1一、热量 ( Heat)
-
1.6.2.2二、功(Work)
-
1.6.2.3三、体积功的计算(Calculation of Volume Work)
-
1.6.2.4四、可逆过程与可逆体积功的计算(Reversible process and Calculation...
-
1.6.3第三节 热力学第一定律(First Law of Thermodynamics)
-
1.6.3.1一、热力学能与热力学第一定律的表达(Thermodynamic Energy and Stateme...
-
1.6.3.2二、恒容热、恒压热与焓( Heat at Constant Volume, Heat at Cons...
-
1.6.3.3三、热容(Heat Capacity)
-
1.6.4第四节 理想气体的热力学性质(Thermodynamic Properties of an Idea...
-
1.6.4.1一、理想气体的热力学能和焓(Thermodynamic Energy and Enthalpy of...
-
1.6.4.2二、理想气体单纯状态变化过程四个物理量的计算(Calculations of the Four Qu...
-
1.6.5第五节 热力学第一定律在相变化中的应用(Application of The First Law i...
-
1.6.5.1一、相变过程的相变焓与相变功(Enthalpy Change and Work for Phase ...
-
1.6.5.2二、热力学第一定律的某些物理量在相变过程中的计算(Calculations of Q, W, ΔU,...
-
1.6.6第六节 热力学第一定律在真实气体节流过程中的应用——焦耳—汤姆生效应(Applications of...
-
1.6.6.1一、焦耳—汤姆生实验(Joule—Thomson Experiment)
-
1.6.6.2二、节流膨胀的热力学特征(Thermodynamics Characteristic of Thro...
-
1.6.7第七节 热力学第二定律(The Second Law of Thermodynamics)
-
1.6.7.1一、过程的不可逆性与可逆性(Irreversibility and Reversibility fo...
-
1.6.7.2二、第二类永动机的不可能性及卡诺定理(Second Kind of Perpetual Motion...
-
1.6.7.3三、热力学第二定律(Second Law of Thermodynamics)
-
1.6.7.4四、熵的物理意义——Boltzmann熵定理
-
1.6.8第八节 熵变的计算(Calculation of Entropy Change)
-
1.6.8.1一、单纯p,V,T变化过程熵变的计算(Calculation of p, V, T Process)
-
1.6.8.2二、理想气体恒温恒压下混合过程的熵变Δ<span title="pagenumber_ebook=6...
-
1.6.8.3三、纯物质相变化过程熵变的计算(Calculation of Phase Transitions)
-
1.6.9第九节 亥姆霍兹自由能及吉布斯自由能(Helmholtz Free Energy and Gibbs...
-
1.6.9.1一、亥姆霍兹自由能(Helmholtz Free Energy)
-
1.6.9.2二、吉布斯自由能(Gibbs Free Energy)
-
1.6.9.3三、ΔA和ΔG的计算(Calculations of the Change in Helmholtz...
-
1.6.10第十节 热力学函数的基本关系式(Basic Relations of Thermodynamic F...
-
1.6.10.1一、热力学基本方程(The Master Equations of Thermodynamics)
-
1.6.10.2二、对应系数关系式(Relations of The Corresponding Coefficie...
-
1.6.10.3三、麦克斯韦关系式(The Maxwell Relations)
-
1.6.10.4四、热力学状态方程(Thermodynamic Equations of State)
-
1.6.10.5五、其他重要关系式(Other Important Relations)
-
1.7第三章 化学反应热力学(Thermodynamics for Chemical Reactions)
-
1.7.1第一节 热化学与反应焓( Thermochemistry and Enthalpy of React...
-
1.7.1.1一、化学反应进度(Extent of Chemical Reaction)
-
1.7.1.2二、热化学方程式(Thermochemical Equation)
-
1.7.1.3三、恒压反应热与恒容反应热的关系(Relation Between Heat of Isobaric...
-
1.7.1.4四、盖斯定律(Hess's Law)
-
1.7.1.5五、标准摩尔生成焓(Standar Molar Enthalpy of Formation)
-
1.7.1.6六、标准摩尔燃烧焓(Standard Molar Combustion Enthalpy)
-
1.7.1.7七、键焓( Bond Enthalpy)
-
1.7.2第二节 反应焓与温度的关系——基尔霍夫定律(Kirchhoff's Law<br />for the...
-
1.7.2.1一、基尔霍夫定律(Kirchhoff's Law)
-
1.7.2.2二、绝热反应最高反应温度的计算(Calculation of Most High-Temperatu...
-
1.7.3第三节 热力学第三定律与标准熵(The Third Law of Thermodynamics an...
-
1.7.3.1一、热力学第三定律的经典表述(Classical Statements of The Third L...
-
1.7.3.2二、规定熵与标准熵(Conventional Entropy and Standard Entrop...
-
1.7.3.3三、化学反应熵变<img title="pagenumber_ebook=89,pagenumber...
-
1.7.4第四节 温度对吉布斯自由能的影响——吉布斯—亥姆霍兹方程(The Effect of Tempera...
-
1.7.4.1一、吉布斯—亥姆霍兹方程(Gibbs-Helmholtz Equation)
-
1.7.4.2二、吉布斯—亥姆霍兹方程的积分式(Integration of Gibbs-Helmholtz Eq...
-
1.7.4.3三、压力对吉布斯自由能的影响(Pressure Dependence of Gibbs Free E...
-
1.7.5*第五节 非平衡态热力学与耗散结构(Nonequilibrium Thermodynamics an...
-
1.7.5.1一、局域平衡(Local Equilibrium)假设
-
1.7.5.2二、熵产生原理(Principle of Entropy Production)
-
1.7.5.3三、线性唯象方程(Phenomenological Linear Equations)
-
1.7.5.4四、昂色格倒易关系(Onsager's Reciprocal Relations)
-
1.7.5.5五、最小熵产生原理(Principle of Minimum Entropy Production)
-
1.7.5.6六、耗散结构(The Dissipative Structure)
-
1.8第四章 溶液一多组分系统热力学(Thermodynamics of Multi-Component ...
-
1.8.1第一节 引 言(Introduction)
-
1.8.2第二节 偏摩尔量(Partial Molar Quantity)
-
1.8.2.1一、偏摩尔量的定义(Definition of Partial Molar Quantity)
-
1.8.2.2二、偏摩尔量的公式(Equation of Partial Molar Quantity)
-
1.8.2.3三、偏摩尔量的测定(Determination of Partial Molar Quantity)
-
1.8.3第三节 化学势(Chemical Potential)
-
1.8.3.1一、化学势的定义(Definition of Chemical Potential)
-
1.8.3.2二、相平衡条件(Condition of Phase Equilibrium)
-
1.8.4第四节 气体热力学(Thermodynamics of Gases)
-
1.8.4.1一、理想气体的化学势(Chemical Potential of Ideal Gases)
-
1.8.4.2二、理想混合气体的化学势(Chemical Potential of Mixture Ideal G...
-
1.8.4.3三、非理想气体的化学势(Chemical Potential of Non-ideal Gas)
-
1.8.4.4四、混合非理想气体(Non-ideal Mixture Gases)
-
1.8.5第五节 拉乌尔定律和亨利定律(Raoult's and Henry's Law)
-
1.8.5.1一、拉乌尔定律(Raoult's Law)
-
1.8.5.2二、亨利定律(Henry's Law)
-
1.8.6第六节 理想溶液(Ideal Solution)
-
1.8.6.1一、理想溶液的定义(Definition of Ideal Solution)
-
1.8.6.2二、理想溶液的通性(Mixing Property of Ideal Solution)
-
1.8.7第七节 稀溶液(Dilute Solution)
-
1.8.7.1一、各组分的化学势(Chemical Potential of a Component)
-
1.8.7.2二、稀溶液的依数性(Colligative Properties of Dilute Solutio...
-
1.8.8第八节 非理想溶液(Non-ideal Solution)
-
1.8.8.1一、活度的定义(Definition of Activity)
-
1.8.8.2二、活度系数的测定(Measurement of Activity Coefficient)
-
1.8.9第九节 分配定律(Distribution Law)
-
1.9第五章 化学平衡(Chemical Equilibrium)
-
1.9.1第一节 化学反应的平衡条件(Equilibrium Conditions for Chemical ...
-
1.9.1.1一、引言(Introduction)
-
1.9.1.2二、化学平衡的条件(Equilibrium Conditions)
-
1.9.2第二节 化学反应的平衡常数(Equilibrium Constants of Chemical Re...
-
1.9.2.1一、理想气体反应的平衡常数(Equilibrium Constants of Ideal-Gas R...
-
1.9.2.2二、实际气体反应的标准平衡常数(Standard Equilibrium constants of ...
-
1.9.2.3三、其他反应的标准平衡常数(Standard Equilibrium Constants of Ot...
-
1.9.2.4*四、弱电解质溶液中的电离平衡简介(Brief Introduction on Ionization...
-
1.9.2.5*五、难溶电解质的溶解平衡(Solubility Equilibrium of Hard Disso...
-
1.9.3第三节 纯凝聚相与理想气体的反应(Reactions of Pure Condensed Matte...
-
1.9.3.1一、纯凝聚相与理想气体的反应(Reactions of Pure Condensed Matter ...
-
1.9.3.2二、分解压(Decomposition Pressure)
-
1.9.4第四节 化学反应等温方程(Isothermic Equation of Chemical React...
-
1.9.5第五节 平衡常数的计算(Calculation of Equilibrium Constants)
-
1.9.5.1一、标准生成吉布斯能法(Method of Standard Molar Gibbs Energy ...
-
1.9.5.2二、标准熵法(Method of Standard Molar Entropy)
-
1.9.5.3三、组合法(Association Method)
-
1.9.6第六节 平衡移动(Movement of Equilibrium)
-
1.9.6.1一、温度对化学平衡的影响(Influence of Temperature on Chemical ...
-
1.9.6.2二、压力对化学平衡的影响(Influence of Pressure on Chemical Equ...
-
1.9.6.3三、惰性组分对化学平衡的影响(Influence of Inert Component on Che...
-
1.9.6.4四、浓度对化学平衡的影响(Influence of Concentration on Chemica...
-
1.9.7第七节 平衡组成的计算(Calculation for Equilibrium Compositio...
-
1.9.8第八节 同时平衡(Simultaneous Equilibrium)
-
1.10第六章 统计热力学基础(Statistical Thermodynamics)
-
1.10.1第一节 概 论(Introduction)
-
1.10.1.1一、统计热力学的研究方法和任务(Research Method and Mission of Sta...
-
1.10.1.2二、统计系统的分类(Classification of Statistical Systems)
-
1.10.1.3三、斯特林(Stirling) 公式
-
1.10.2第二节 分子的运动形式及能级公式(Motion Forms of Molecules and Ene...
-
1.10.2.1一、分子的运动形式(Motion Forms of Molecules)
-
1.10.2.2二、平动能级(Translational Energy Level)
-
1.10.2.3三、转动能级(Rotational Energy Level)
-
1.10.2.4四、振动能级(Vibrational Energy Level)
-
1.10.2.5五、电子运动能级和核运动能级(Energy Level of Electronic and Nucl...
-
1.10.2.6六、分子能级(Molecular Energy Level)
-
1.10.3第三节 粒子的能量分布和独立粒子系统的微观状态数( Energy Distribution of P...
-
1.10.3.1一、宏观状态和微观状态(Macrostate and Microstate)
-
1.10.3.2二、能量分布(Energy Distribution)
-
1.10.3.3三、定位系统的微观状态数(Microstate Number of Located System)
-
1.10.3.4四、非定位系统的微观状态数(Microstate Number of Non-located Sys...
-
1.10.4第四节 最概然分布(The Most Probable Distribution)
-
1.10.4.1一、统计热力学的基本假定(Basic Hypothesis of Statistical Therm...
-
1.10.4.2二、玻耳兹曼定理(Boltzmann's Theorem)
-
1.10.4.3三、最概然分布(Most Probable Distribution)
-
1.10.5第五节 玻耳兹曼分布定律(Law of Boltzmann Distribution)
-
1.10.5.1一、玻耳兹曼分布定律的推导(Derivation of Boltzmann Distribution...
-
1.10.5.2二、玻耳兹曼分布定律(Boltzmann Distribution Law)
-
1.10.5.3*三、玻色-爱因斯坦分布和费米-狄拉克分布(Bose-Einstein and Femi。-Dira...
-
1.10.5.4四、配分函数(Partition Function)
-
1.10.6第六节 配分函数与热力学函数的关系(Relation Between Partition Funct...
-
1.10.6.1一、非定位系统的热力学函数(Thermodynamic Function of Non-locate...
-
1.10.6.2二、定位系统的热力学函数(Thermodynamic Function of Located Sys...
-
1.10.7第七节 热力学三大定律的本质(Essence of Thermodynamics Law )
-
1.10.7.1一、热力学第一定律的本质(Essence of First Law of Thermodynamic...
-
1.10.7.2二、热力学第二定律的本质(Essence of Second Law of Thermodynami...
-
1.10.7.3三、热力学第三定律的本质(Essence of Third law of Thermodynamic...
-
1.10.8第八节 配分函数的计算(Calculation of Partition Function)
-
1.10.8.1一、平动配分函数(Translational Partition Function)
-
1.10.8.2二、转动配分函数(Rotational Partition Function)
-
1.10.8.3三、振动配分函数(Vibrational Partition Function)
-
1.10.8.4四、电子配分函数(Electronic Partition Function)
-
1.10.8.5五、核配分函数(Nucleus Partition Function)
-
1.10.9第九节 统计熵的计算(Calculation of Statistical Entropy )
-
1.10.9.1一、平动熵(Translational Entropy)
-
1.10.9.2二、转动熵(Rotational Entropy)
-
1.10.9.3三、振动熵(Vibrational Entropy)
-
1.10.9.4四、电子熵( Electronic Entropy)
-
1.10.10第十节 统计热力学原理应用示例(Applied Examples of Principles of ...
-
1.10.10.1一、理想气体状态方程的导出(Derivation of State Equation of Idea...
-
1.10.10.2二、气体热容的计算(Calculation of Heat Capacity of Gas )
-
1.10.10.3三、理想气体反应平衡常数的计算(Calculation of Equilibrium Constan...
-
1.11第七章 电化学(Electrochemistry)
-
1.11.1第一节 引 言(Introduction)
-
1.11.1.1一、电化学的用途(Electrochemistry and Its Application)
-
1.11.1.2二、导体的分类(Classification of Conductors)
-
1.11.1.3三、正极和负极(Positive and Negative Electrode )
-
1.11.1.4四、阴极和阳极(Cathode and Anode)
-
1.11.1.5五、离子迁移方向(Direction of Ionic Migration)
-
1.11.2第二节 电化学基本概念和法拉第定律(Faraday' Laws)
-
1.11.2.1一、电解池(Electrolyte Cell)
-
1.11.2.2二、原电池(Primary Cell)
-
1.11.2.3三、法拉第定律(Faraday' Laws)
-
1.11.2.4四、电量计(Coulometer)
-
1.11.3第三节 离子的电迁移和迁移数(Ionic Electric Transport and Transf...
-
1.11.3.1一、离子的电迁移现象(Ions Electro-migration Phenomenon)
-
1.11.3.2二、离子电迁移率(Ionic Electro-mobility)
-
1.11.3.3三、离子的迁移数(Ionic Transference Number)
-
1.11.3.4四、离子的电迁移率与迁移数的关系(Relation Between Ionic Electro-mo...
-
1.11.3.5五、离子迁移数的测定(Determination of Ionic Transference Num...
-
1.11.4第四节 电解质溶液的电导(Electric Conductance of Electrolyte S...
-
1.11.4.1一、电导、电导率、摩尔电导率(Conductance, Conductivity and Molar...
-
1.11.4.2二、电导率、摩尔电导率与浓度的关系
-
1.11.4.3三、离子独立运动定律(Law of The Independent Migration of Ion...
-
1.11.4.4四、电导的测定及其一些应用(Measurement of Conductance and Its A...
-
1.11.5第五节 电解质溶液离子的平均活度和平均活度系数(Mean Activity and Mean Act...
-
1.11.5.1一、平均活度和平均活度系数(Mean Activity and Mean Activity Coef...
-
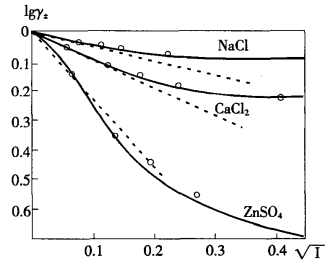
1.11.5.2二、离子平均活度系数与浓度的关系(Relation Between Mean Activity Co...
-
1.11.5.3三、德拜—休克尔离子互吸理论(Debye-Hückel Interionic Attraction ...
-
1.11.6第六节 氧化还原反应(Oxidation and Reduction Reaction)
-
1.11.6.1一、氧化值(Oxidation Number)
-
1.11.6.2二、氧化还原反应方程式的配平(Balance of Ox-red Reaction Equation...
-
1.11.7第七节 可逆电池及其电动势(Reversible Cell and Its Electromotiv...
-
1.11.7.1一、可逆电池和不可逆电池(Reversible and Irreversible Cell)
-
1.11.7.2二、可逆电池电动势的测定及电池的表示方法(Measurement of E.M.F and Reve...
-
1.11.7.3三、可逆电池电动势与参加反应的各物质活度的关系(Activities of Each Compone...
-
1.11.7.4四、可逆电池电动势和温度的关系(Temperature Dependence of E.M.F of...
-
1.11.8第八节 电极电势和可逆电极(Electrode Potential and Reversible E...
-
1.11.8.1一、电极与溶液界面电势差(Potential Difference at Electrode/Sol...
-
1.11.8.2二、电极电势(Electrode Potential)
-
1.11.8.3三、电极电势与参加反应物质活度的关系(Activities of Each Component in...
-
1.11.8.4四、可逆电极(Reversible Electrode)
-
1.11.9第九节 浓差电池和液体接界电势(Concentration Cell and Liquid Junc...
-
1.11.9.1一、浓差电池(Concentration Cell)
-
1.11.9.2二、液体接界电势(Liquid Junction Potential)
-
1.11.10第十节 电动势法的应用(Determination of E.M.F and Its Applica...
-
1.11.10.1一、求化学反应的吉布斯自由能变化(Calculation of Gibss Free Energy ...
-
1.11.10.2二、测定化学反应的焓变和熵变(Determination of Enthalpy and Entro...
-
1.11.10.3三、溶液pH的测量 (Measurement of pH Value of Solution)
-
1.11.11*第十一节 电势-pH图(E~pH Diagram)
-
1.11.11.1一、无<img title="pagenumber_ebook=213,pagenumber_boo...
-
1.11.11.2=、有<img title="pagenumber_ebook=213,pagenumber_boo...
-
1.11.11.3三、有<img title="pagenumber_ebook=213,pagenumber_boo...
-
1.11.12*第十二节 熔盐电池(Molten Salt Cell)
-
1.11.12.1一、熔盐原电池(Molten Salt Cell)
-
1.11.12.2二、熔盐电池的电极电势(Electrode Potential of Molten Salt Cel...
-
1.11.12.3三、熔盐电池的应用(Application of E.M.F of Molten Salt Cell...
-
1.11.13*第十三节 固体电解质电池(Solid Electrolyte Cell)
-
1.11.13.1一、固体电解质的导电机理(Conducting Mechanism of Solid Electro...
-
1.11.13.2二、固体电解质电池的应用(Application of Solid Electrolyte Cell...
-
1.11.14第十四节 电解与极化作用(Electrolysis and Polarization)
-
1.11.14.1一、电解与分解电压(Electrolysis and Decomposition Voltage)
-
1.11.14.2二、极化作用与超电势(Polarization and Over Potential)
-
1.11.14.3三、浓差极化和活化极化(Concentration and Activation Polarizat...
-
1.11.14.4四、超电势的测量( Measurement of Overpotential)
-
1.11.14.5五、氢超电势(Hydrogen Overpotential)
-
1.11.15第十五节 电解时电极上的电化学反应(Electrode Reaction at Electrolys...
-
1.11.15.1一、金属的阴极析出及阳极溶出(Cathode Deposition and Anode Dissol...
-
1.11.15.2二、金属的电解分离和共沉积(Electrolysis Separation and Co-depos...
-
1.11.15.3三、化学物质的制备(Preparation of Chemical Material)
-
1.11.16第十六节 金属的电化学腐蚀与防护(Metal Electrochemical Corrosion a...
-
1.11.16.1一、金属的腐蚀(Metal Corrosion)
-
1.11.16.2二、电化学腐蚀(Electrochemical Corrosion)
-
1.11.16.3三、金属的防腐蚀(Metal Anti-corrosion)
-
1.11.17第十七节 化学电源(Chemical Battery)
-
1.11.17.1一、一次电池(Primary Battery)
-
1.11.17.2二、蓄电池或二次电池(Secondary Battery)
-
1.11.17.3三、燃料电池(Fuel Cell)
-
1.12第八章 化学动力学(Chemical Kinetics)
-
1.12.1第一节 引 言(Introduction)
-
1.12.1.1一、化学动力学的任务、目的和发展(Mission, Purpose and Development ...
-
1.12.1.2二、反应速率表示法(Reaction-Rate Expression)
-
1.12.1.3三、反应速率的测定(Measurement of Reaction Rates)
-
1.12.2第二节 化学反应的速率方程式(Chemical Reaction-Rate Equations)
-
1.12.2.1一、基元反应的速率方程式(Rate Laws for Elementary Reactions)
-
1.12.2.2二、复合反应的速率方程式(Complex Reaction Rate Equations)
-
1.12.3第三节 反应速率方程的积分形式(Integrated Rate Laws)
-
1.12.3.1一、零级反应(Zeroth Order Reactions)
-
1.12.3.2二、一级反应(First-Order Reactions)
-
1.12.3.3三、二级反应(Second-Order Reactions)
-
1.12.3.4四、n级反应(n-Order Reaction)
-
1.12.4第四节 反应级数的确定(Determination for Order of Reaction)
-
1.12.4.1一、积分法(Integral Method)
-
1.12.4.2二、半衰期法(Half-life Method )
-
1.12.4.3三、微分法(Differential Method )
-
1.12.4.4*四、微分反应器和积分反应器(Differential Reactor and Integral R...
-
1.12.5第五节 温度对反应速率的影响(Influence of Temperature on Reactio...
-
1.12.5.1一、阿伦尼乌斯公式(Arrhenius Formula)
-
1.12.5.2二、活化能(Activation Energy)
-
1.12.6第六节 基元反应速率理论简介(Brief Introduction of Elementary Re...
-
1.12.6.1一、简单碰撞理论(Simple Collision Theory)
-
1.12.6.2*二、过渡状态理论(Transition-State Theory)
-
1.12.7第七节 典型的复合反应(Typical Complex Reactions)
-
1.12.7.1一、对峙反应(Opposing Reaction)
-
1.12.7.2二、平行反应(Parallel Reactions)
-
1.12.7.3三、连串反应(Consecutive Reactions)
-
1.12.7.4四、链式反应(Chain Reactions)
-
1.12.7.5五、平衡态近似法和稳态近似法(Pre-Equilibrium Approximation and S...
-
1.12.8*第八节 多相反应动力学(Heterogeneous Reaction Kinetics)
-
1.12.8.1一、菲克扩散第一定律(Fick's First Law of Diffusion)
-
1.12.8.2二、受扩散过程控制的多相反应(Diffusion-controlled Heterogeneous ...
-
1.12.8.3三、总反应速率与扩散和化学反应两步骤的关系(Relation of Total Reaction-R...
-
1.12.8.4四、固体与气体的反应(Reactions of Solid to Gas)
-
1.12.9*第九节 溶液中的反应(Reactions in Solutions)
-
1.12.9.1一、笼子效应(Cage Effect)
-
1.12.9.2二、溶液反应的动力学(Kinetics of Solution Reaction)
-
1.12.9.3三、溶剂对反应物无明显作用(No Obvious Solvent Action on Reactan...
-
1.12.9.4四、溶剂对反应物分子有明显作用(Having Obvious Solvent Action on R...
-
1.12.10第十节 催化作用(Catalytic Action)
-
1.12.10.1一、催化作用的一般机理(General Mechanism of Catalytic Action)
-
1.12.10.2二、催化反应的基本特征(Basic Characteristics of Catalytic Rea...
-
1.12.10.3三、酸碱催化反应(Reaction Catalyzed Acids and Alkalis)
-
1.12.10.4四、络合催化反应(Complex Catalysis Reactions)
-
1.12.10.5*五、酶催化(Enzyme Catalysis)
-
1.12.11*第十一节 光化学反应(Photochemical Reactions)
-
1.12.11.1一、光化学基本定律(Fundamental Laws of Photochemistry)
-
1.12.11.2二、量子效率(Quantum Yield)
-
1.12.11.3三、光化学反应机理及速率方程(Photochemical Reaction Mechanism an...
-
1.13第九章 相平衡(Phase Equilibrium)
-
1.13.1第一节 相律(Phase Rule)
-
1.13.1.1一、基本概念(Fundamental Concept)
-
1.13.1.2二、相律(Phase Rule)
-
1.13.2第二节 单组分系统相图(Phase Diagram of One-component Systems...
-
1.13.2.1一、克拉佩龙方程式(Clapeyron Equation)
-
1.13.2.2二、克劳修斯—克拉佩龙方程式(Clausius-Clapeyron Equation)
-
1.13.2.3三、单元系相图(One-component Phase Diagrams)
-
1.13.3第三节 二元系气—液平衡相图(Two-component Liquid-vapor Equilibr...
-
1.13.3.1一、蒸气压一组成图(p-x图) (Pressure Composition Diagram)
-
1.13.3.2二、沸点组成图(T-x图) (Temperature Composition Diagram)
-
1.13.4第四节 液态部分互溶的二元系(Two-component Systems for Two Parti...
-
1.13.5第五节 完全不互溶的双液系统(Two-component Systems for Two Immis...
-
1.13.6第六节 简单低共熔混合物的固—液二元系相图(Two-component Solid-liquid P...
-
1.13.6.1一、热分析法绘制相图(Determination a Phase Diagram by Therma...
-
1.13.6.2二、Bi—Cd系相图(Bi—Cd Phase Diagram)
-
1.13.6.3三、溶解度法及水—盐系统的相图(Determination Phase Diagram for Wa...
-
1.13.7第七节 生成化合物的固—液二元系相图(Compound Formation-Two Componen...
-
1.13.7.1一、生成稳定化合物的二元系(Two Component System of Steady Compo...
-
1.13.7.2二、生成不稳定化合物的二元系(Two Component System of Unstable Co...
-
1.13.8第八节 生成连续固溶体的二元系(Two Component System Formation Con...
-
1.13.9第九节 固态部分互溶的二元系(Two-component System of Solid-phase...
-
1.13.9.1一、固态部分互溶的共晶类型(Solid-phase Partially Miscible with ...
-
1.13.9.2二、固态部分互溶的包晶类型(Solid-phase Partially Miscible with ...
-
1.13.9.3三、区域熔炼(Zone Melting)
-
1.13.10第十节 三元系相图(Three-Component Systems Phase Diagram)
-
1.13.10.1一、三角坐标——等边三角形法(Triangular Coordinate-Equilateral T...
-
1.13.10.2二、三角坐标的特点(Characteristics of Triangular Coordinate...
-
1.13.11第十一节 生成简单共晶的三元系(Three-component Systems With Simpl...
-
1.13.11.1一、立体图(Three Dimensional Diagrams)
-
1.13.11.2二、投影图(Projective Diagrams)
-
1.13.11.3三、冷却过程(Cooling Process)
-
1.13.12*第十二节 部分互溶的三液体系统(Three-component Systems for Parti...
-
1.13.12.1一、一对部分互溶的系统(Partially Miscible Between one Couple ...
-
1.13.12.2二、有两对及三对部分互溶的系统(Partially Miscible Between Two or ...
-
1.13.12.3三、萃取过程(Extraction Process)
-
1.13.13*第十三节 三元水盐系相图(Three-component Water-salt Systems P...
-
1.13.14*第十四节 高级相变(Higher—order Phase Transitions)
-
1.14第十章 表面化学(Surface Chemistry)
-
1.14.1第一节 表面吉布斯自由能与表面热力学的基本方程(Gibbs Free Energy of surfa...
-
1.14.1.1一、分散度与比表面A<span title="pagenumber_ebook=319,pagenu...
-
1.14.1.2二、表面张力及热力学定义(Surface Tension and Thermodynamic Def...
-
1.14.1.3三、表面热力学基本方程(Fundamental Equations of Surface Therm...
-
1.14.1.4四、影响表面张力的因素(Affecting Factors of Surface Tension)
-
1.14.2第二节 弯曲液面的附加压力—拉普拉斯方程(The Additional Pressure of Cu...
-
1.14.2.1一、附加压力Δp ( Additional Pressure)
-
1.14.2.2二、附加压力Δp与曲率半径r的关系—Laplace方程(Relation Between Addit...
-
1.14.2.3三、最大气泡压力法测定表面张力(Measurement of Surface Tension by ...
-
1.14.3第三节 润湿现象与杨方程式(Wetting and The Young Equation)
-
1.14.3.1一、润湿及其分类(Wetting and Its Classification)
-
1.14.3.2二、接触角与Young方程式(Contact Angle and Young Equation)
-
1.14.3.3三、润湿的应用(Applications of Wetting)
-
1.14.4第四节 分散度对物质性质的影响(The Effect of Dispersity Upon Mate...
-
1.14.4.1一、微小液滴的饱和蒸气压—Kelvin方程(Saturated Vapor Pressure of ...
-
1.14.4.2二、微小晶体的溶解度与曲率半径的关系—Kelvin方程(Relation Between the S...
-
1.14.4.3三、新相生成与亚稳状态(Formation of New Phase and Metastable ...
-
1.14.4.4四、分散度对物质化学活性的影响(Influence of Dispersity on Chemica...
-
1.14.5第五节 气体在固体上的吸附(Adsorption of Gases at Solid)
-
1.14.5.1一、吸附作用(Adsorption)
-
1.14.5.2二、物理吸附与化学吸附(Physical and Chemical Adsorption)
-
1.14.5.3三、吸附量与吸附热力学(Adsorption Quantity and Thermodynamics...
-
1.14.5.4四、吸附曲线(Adsorption Curve)
-
1.14.5.5五、吸附等温式(Absorption Isothermal Formula)
-
1.14.5.6六、固体自溶液中的吸附(Adsorption of Solid From Solution)
-
1.14.6第六节 溶液表面的吸附作用(Adsorption of Solution Surface)
-
1.14.6.1一、溶液表面的吸附现象(Adsorption Phenomenon of Solution Surf...
-
1.14.6.2二、Gibbs吸附等温方程式(Gibbs Adsorption Isotherm Equation)
-
1.14.6.3*三、吉布斯吸附等温式的推导(Derivation for Gibbs Adsorption Iso...
-
1.14.6.4四、Gibbs吸附等温方程式的应用(Application for Gibbs Adsorption...
-
1.14.6.5五、表面活性剂(Surfactant)
-
1.15第十一章 胶体化学(Colloid Chemistry)
-
1.15.1第一节 胶体系统的分类及特征(Classification and Characteristics ...
-
1.15.1.1一、引言(Introduction)
-
1.15.1.2二、胶体的分类(Colloidal Classification)
-
1.15.1.3三、胶体的特征(Colloidal Characteristics)
-
1.15.2第二节 胶体系统的制备与提纯(Preparation and Purification of Col...
-
1.15.2.1一、分散法(Dispersion Methods)
-
1.15.2.2二、凝聚法(Condensation Methods)
-
1.15.2.3三、溶胶的提纯(Purification of Collosol)
-
1.15.3第三节 胶体系统的光学性质(Optical Characters of Colloidal Syst...
-
1.15.3.1一、丁铎尔效应(Tyndall Effect)
-
1.15.3.2二、瑞利公式(Rayleigh Formula)
-
1.15.3.3三、超显微镜与粒子大小的近似测定(Ultramicroscope and Approximate D...
-
1.15.4第四节 胶体系统的动力性质(Dynamic Characters of Colloidal Syst...
-
1.15.4.1一、布朗运动(Brown Movement)
-
1.15.4.2二、扩散(Diffusion)
-
1.15.4.3三、沉降与沉降平衡(Sedimentation and Sedimentation Equilibr...
-
1.15.5第五节 溶胶系统的电学性质(Electricity Properties of Collosol S...
-
1.15.5.1一、双电层理论(Electric Double Layer Theory)
-
1.15.5.2二、溶胶的电动现象(Electrokinetic Phenomenon of Collosol )
-
1.15.6第六节 溶胶的胶团结构(Structure of Colloidal Lump)
-
1.15.7第七节 溶胶的稳定与聚沉(Stabilizing and Coagulation of Collos...
-
1.15.7.1一、溶胶的稳定性(Stability of Collosol)
-
1.15.7.2二、溶胶的聚沉(Coagulation of Collosol)
-
1.15.8第八节 高分子化合物溶液(Solutions of Polymer Compounds)
-
1.15.8.1一、高分子化合物的相对分子质量(Relative Molecular Mass of Polymer...
-
1.15.8.2二、高分子溶液的黏度(Viscosity of Polymer Solutions)
-
1.15.8.3三、高分子溶液的渗透压和唐南平衡(Osmotic Pressure and Donnan Equil...
-
1.15.8.4四、盐析作用和胶凝作用(Salting-out Action and Gelatination)
-
1.16附 录
-
1.17参考文献
1
物理化学