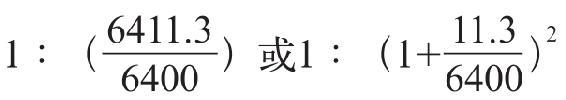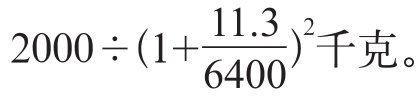-
1.1作者简介
-
1.2第1章 地球和它的运动
-
1.2.11.1 地球上和地图上的最短航线
-
1.2.21.2 经度和纬度
-
1.2.31.3 阿蒙森是往哪个方向飞的?
-
1.2.41.4 五种计时法
-
1.2.51.5 白昼的长短
-
1.2.61.6 不同寻常的阴影
-
1.2.71.7 一道关于两列火车的题目
-
1.2.81.8 用怀表找方向
-
1.2.91.9 白夜和黑昼
-
1.2.101.10 光明与黑暗的交替
-
1.2.111.11 极地太阳的一个谜
-
1.2.121.12 四季始于何时?
-
1.2.131.13 三个“假如”
-
1.2.141.14 再一个“假如”
-
1.2.151.15 我们什么时候离太阳更近些:中午还是傍晚?
-
1.2.161.16 再远一米
-
1.2.171.17 从不同的角度来看
-
1.2.181.18 非地球时间
-
1.2.191.19 年月从何时开始?
-
1.2.201.20 2月有几个星期五?
-
1.3第2章 月球和它的运动
-
1.3.12.1 是新月还是残月?
-
1.3.22.2 月亮的位相
-
1.3.32.3 孪生行星
-
1.3.42.4 为什么月亮不会掉到太阳上去?
-
1.3.52.5 月亮看得见的一面和看不见的一面
-
1.3.62.6 第二个月亮和月亮的月亮
-
1.3.72.7 月球上为什么没有大气?
-
1.3.82.8 月球世界的大小
-
1.3.92.9 月球上的风景
-
1.3.102.10 月球上的天空
-
1.3.112.11 天文学家为什么要观察日月食?
-
1.3.122.12 为什么日月食每隔18年出现一次?
-
1.3.132.13 可能吗?
-
1.3.142.14 关于日月食的几个大家不很清楚的问题
-
1.3.152.15 月球上有什么样的天气?
-
1.4第3章 行星
-
1.4.13.1 白昼时的行星
-
1.4.23.2 行星的符号
-
1.4.33.3 画不出来的东西
-
1.4.43.4 水星上为何没有大气?
-
1.4.53.5 金星的位相
-
1.4.63.6 大冲
-
1.4.73.7 行星抑或小型的太阳?
-
1.4.83.8 土星环的消失
-
1.4.93.9 天文学上的字谜
-
1.4.103.10 比海王星更远的一颗行星
-
1.4.113.11 小行星
-
1.4.123.12 我们的近邻
-
1.4.133.13 木星的同伴
-
1.4.143.14 别处的天空
-
1.5第4章 恒星
-
1.5.14.1 恒星为何叫恒星?
-
1.5.24.2 为什么恒星会闪烁,而行星的光芒却很稳定?
-
1.5.34.3 白天能看见恒星吗?
-
1.5.44.4 什么是星等?
-
1.5.54.5 恒星代数学
-
1.5.64.6 眼睛和望远镜
-
1.5.74.7 太阳和月球的星等
-
1.5.84.8 恒星和太阳的真实亮度
-
1.5.94.9 已知星体中最亮的恒星
-
1.5.104.10 地球天空和其他天空的行星的星等
-
1.5.114.11 望远镜为何不会将恒星放大?
-
1.5.124.12 以前是如何测量恒星的直径的?
-
1.5.134.13 恒星世界的巨人
-
1.5.144.14 出人意料的计算
-
1.5.154.15 最重的物质
-
1.5.164.16 为何把这类星叫做恒星?
-
1.5.174.17 恒星距离的尺度
-
1.5.184.18 最近的恒星系统
-
1.5.194.19 宇宙比例尺
-
1.6第5章 万有引力
-
1.6.15.1 垂直上射的炮弹
-
1.6.25.2 高空中的重量
-
1.6.35.3 使用圆规画行星轨道
-
1.6.45.4 行星向太阳坠落
-
1.6.55.5 赫菲斯托斯的铁砧
-
1.6.65.6 太阳系的边缘
-
1.6.75.7 凡尔纳小说中的错误
-
1.6.85.8 怎么称地球的重量?
-
1.6.95.9 地球的核心是什么?
-
1.6.105.10 太阳和月球的重量
-
1.6.115.11 行星和恒星的重量与密度
-
1.6.125.12 月球上和行星上的重力
-
1.6.135.13 最大的重力
-
1.6.145.14 行星深处的重力
-
1.6.155.15 有关轮船的问题
-
1.6.165.16 月球和太阳所引起的潮汐
-
1.6.175.17 月球和气候
1
趣味天文学
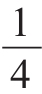 。
。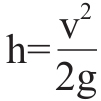
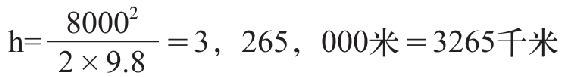
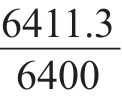 倍。
倍。