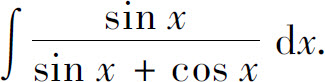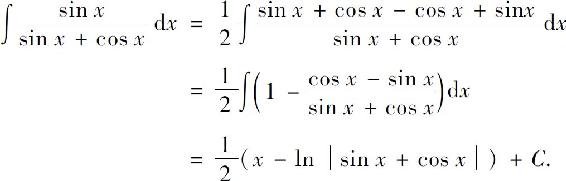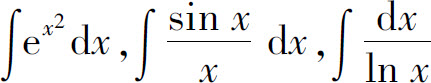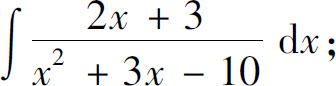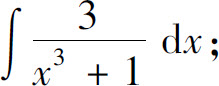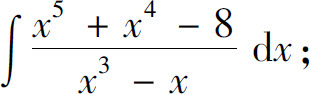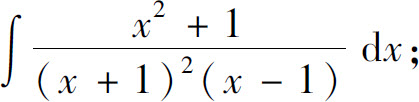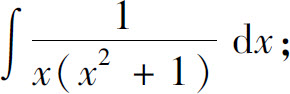-
1.1前言
-
1.2第1章 函数与极限
-
1.2.11.1 函数
-
1.2.21.2 数列极限
-
1.2.31.3 函数极限
-
1.2.41.4 极限存在准则 两个重要极限
-
1.2.51.5 无穷小与无穷大
-
1.2.61.6 函数的连续性
-
1.2.7习题1
-
1.3第2章 导数与微分
-
1.3.12.1 导数的概念
-
1.3.22.2 求导法则
-
1.3.32.3 高阶导数
-
1.3.42.4 隐函数和由参数方程所确定的函数的导数
-
1.3.52.5 微分
-
1.3.6习题2
-
1.4第3章 微分中值定理与导数的应用
-
1.4.13.1 微分中值定理
-
1.4.23.2 洛必达法则
-
1.4.33.3 函数的单调性与极值
-
1.4.43.4 曲线的凹凸性与函数图形的描绘
-
1.4.53.5 曲率
-
1.4.63.6 导数在经济学中的应用
-
1.4.7习题3
-
1.5第4章 不定积分
-
1.5.14.1 不定积分的概念和性质
-
1.5.24.2 换元积分法
-
1.5.34.3 分部积分法
-
1.5.44.4 有理函数的积分
-
1.5.5习题4
-
1.6第5章 定积分及其应用
-
1.6.15.1 定积分的概念与性质
-
1.6.25.2 微积分基本定理
-
1.6.35.3 定积分的换元积分法与分部积分法
-
1.6.45.4 广义积分
-
1.6.55.5 定积分的应用
-
1.6.6习题5
-
1.7第6章 多元函数微积分
-
1.7.16.1 空间直角坐标系及多元函数的概念
-
1.7.26.2 多元函数的极限与连续
-
1.7.36.3 偏导数与全微分
-
1.7.46.4 多元复合函数求导法则与隐函数求导公式
-
1.7.56.5 多元函数的极值
-
1.7.66.6 二重积分
-
1.7.7习题6
-
1.8第7章 常微分方程与差分方程
-
1.8.17.1 微分方程的一般概念
-
1.8.27.2 一阶微分方程
-
1.8.37.3 可降阶的高阶微分方程
-
1.8.47.4 线性微分方程解的结构
-
1.8.57.5 二阶常系数线性微分方程
-
1.8.67.6 差分方程简介
-
1.8.7习题7
-
1.9第8章 无穷级数
-
1.9.18.1 数项级数的概念与性质
-
1.9.28.2 正项级数
-
1.9.38.3 交错级数、绝对收敛与条件收敛
-
1.9.48.4 幂级数
-
1.9.58.5 泰勒级数
-
1.9.68.6 幂级数的应用
-
1.9.7习题8
-
1.10部分习题参考答案
-
1.11参考文献
1
高等数学
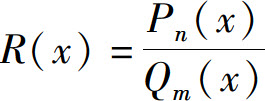 为有理函数或有理分式.当n<m时,称这有理函数为真分式;而当n≥m时,称这有理函数为假分式.
为有理函数或有理分式.当n<m时,称这有理函数为真分式;而当n≥m时,称这有理函数为假分式.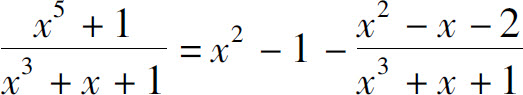
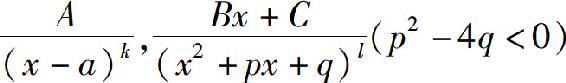
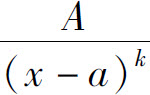 的不定积分容易计算,下面举例说明
的不定积分容易计算,下面举例说明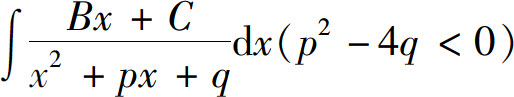 的计算方法.
的计算方法.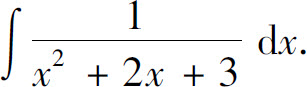
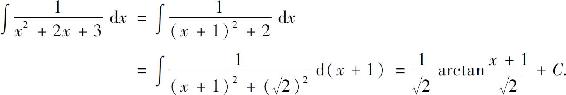
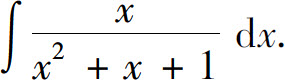
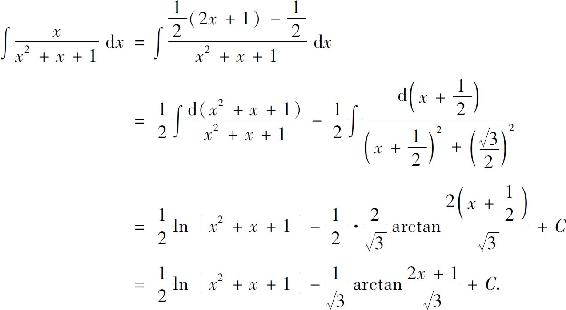
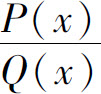 为真分式,如果分母可分解为
为真分式,如果分母可分解为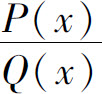 的分解式中应包含
的分解式中应包含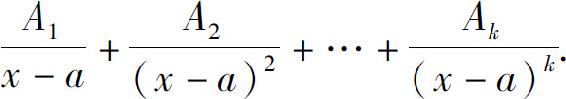
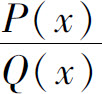 的分解式中应包含
的分解式中应包含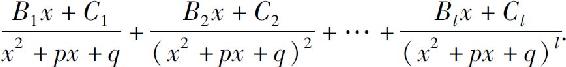
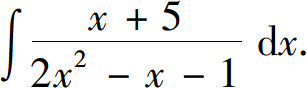
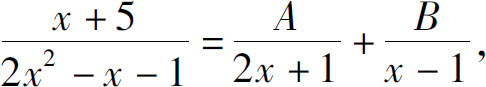
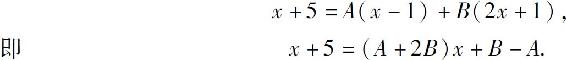

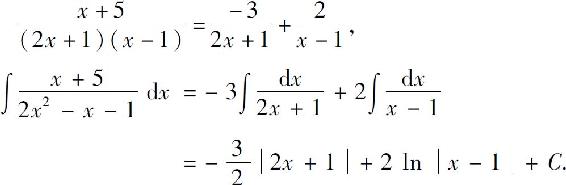
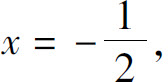 得A=-3;令x=1,得B=2.
得A=-3;令x=1,得B=2.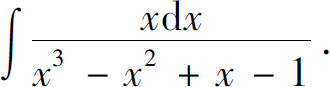

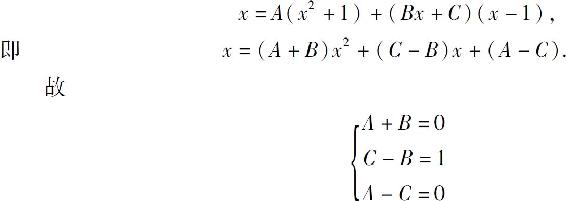
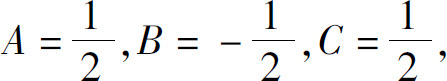 因此
因此
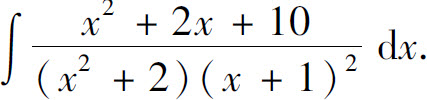
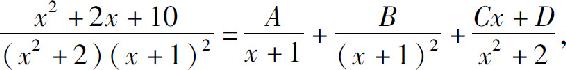
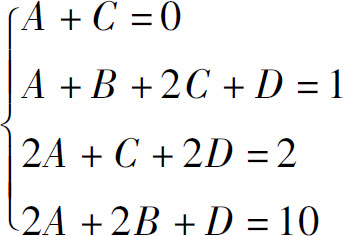
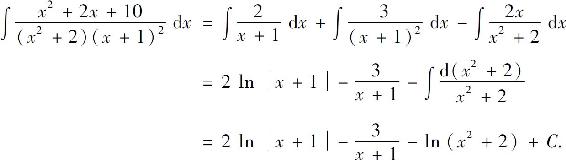
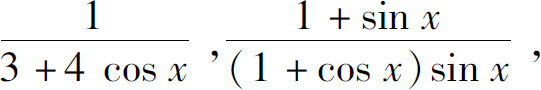
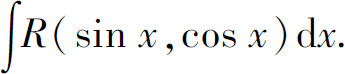
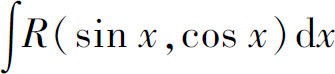 ,可通过变换
,可通过变换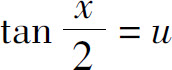 化为关于u的有理函数的积分.因为
化为关于u的有理函数的积分.因为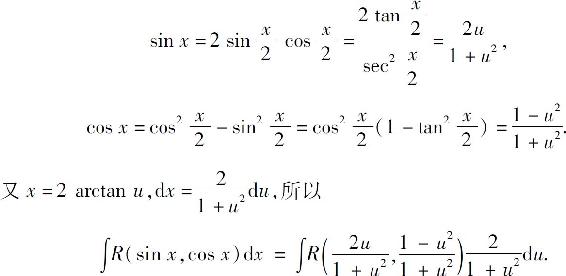
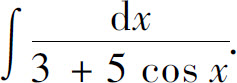
 则
则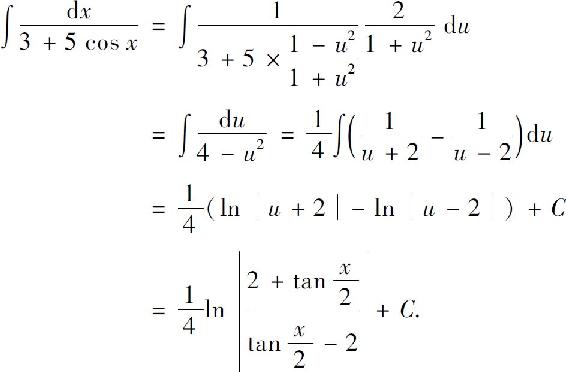
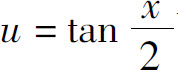 可将三角函数有理式的积分转化为有理函数的积分,但某些三角函数有理式的不定积分用其他方法可能更为简便.
可将三角函数有理式的积分转化为有理函数的积分,但某些三角函数有理式的不定积分用其他方法可能更为简便.