-
1.1实验一 光学多通道分析器的应用
-
1.1.1背景知识
-
1.1.2实验原理
-
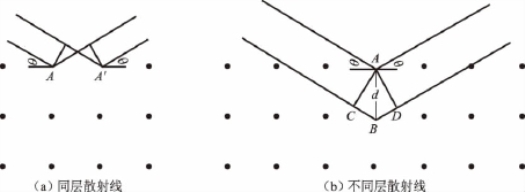
1.1.2.11.光栅分光原理
-
1.1.2.22.光栅的基本特性
-
1.1.3仪器介绍
-
1.1.3.11.仪器结构
-
1.1.3.22.性能指标
-
1.1.4操作步骤
-
1.1.5实验内容
-
1.1.6思考题
-
1.1.7附录1 软件介绍
-
1.1.7.11.“文件”菜单
-
1.1.7.22.“信息”菜单
-
1.1.7.33.“运行”菜单
-
1.1.7.44.“数据处理”菜单
-
1.1.7.55.“系统”菜单
-
1.1.8附录2 三棱镜分光
-
1.1.8.11.基本原理
-
1.1.8.22.棱镜的基本特性
-
1.1.8.33.棱镜的基本类型
-
1.1.9附录3 常用光谱仪简介
-
1.1.9.11.光谱仪
-
1.1.9.22.光谱仪的分类
-
1.1.10附录4 常见光源光谱
-
1.2实验二 微波的光学特性实验
-
1.2.1背景知识
-
1.2.2实验原理
-
1.2.2.11.微波的反射
-
1.2.2.22.微波的单缝衍射
-
1.2.2.33.微波的双缝干涉
-
1.2.2.44.微波偏振
-
1.2.2.55.微波迈克尔逊干涉
-
1.2.3仪器介绍
-
1.2.3.11.DH926B型微波装置
-
1.2.3.22.ZKY-WB-2型微波装置
-
1.2.4试验内容
-
1.2.4.11.微波的反射
-
1.2.4.22.微波的单缝衍射
-
1.2.4.33.微波的双缝干涉
-
1.2.4.44.微波偏振
-
1.2.4.55.微波迈克尔逊干涉
-
1.2.5思考题
-
1.2.6附 录
-
1.2.6.11.电磁波谱及微波的频段划分
-
1.2.6.22.实验数据示例(DH926B微波系统,供参考)
-
1.3实验三 微波布拉格衍射实验
-
1.3.1背景知识
-
1.3.2实验原理
-
1.3.3仪器介绍
-
1.3.4实验内容
-
1.3.4.11.验证布拉格公式
-
1.3.4.22.已知晶格常数测定波长
-
1.3.4.33.已知波长测定晶格常数
-
1.3.5思考题
-
1.3.6附 录
-
1.4实验四 燃料电池综合特性研究
-
1.4.1背景知识
-
1.4.2实验原理
-
1.4.2.11.燃料电池
-
1.4.2.22.水的电解
-
1.4.3仪器介绍
-
1.4.3.11.实验主板
-
1.4.3.22.测试仪
-
1.4.3.33.可变负载
-
1.4.4实验内容
-
1.4.4.11.质子交换膜电解池的特性研究
-
1.4.4.22.燃料电池输出特性的研究
-
1.4.5思考题
-
1.4.6注意事项
-
1.4.7附 录
-
1.5实验五 太阳能电池综合特性研究
-
1.5.1背景知识
-
1.5.2实验原理
-
1.5.3实验仪器
-
1.5.4实验内容
-
1.5.5选做内容
-
1.5.6思考题
-
1.5.7注意事项
-
1.6实验六 夫兰克-赫兹实验
-
1.6.1背景知识
-
1.6.2实验原理
-
1.6.2.11.玻尔的原子理论
-
1.6.2.22.电子与原子碰撞及能量交换
-
1.6.2.33.电子平均自由程对激发或电离的影响
-
1.6.2.44.接触电势差
-
1.6.2.55.原子第一激发电位的测定
-
1.6.3仪器介绍
-
1.6.3.11.实验仪器连接图
-
1.6.3.22.实验仪面板说明
-
1.6.3.33.基本操作
-
1.6.4注意事项
-
1.6.4.11.连线
-
1.6.4.22.保护措施
-
1.6.4.33.工作参数的设置
-
1.6.5实验内容及步骤
-
1.6.5.11.脱机测试
-
1.6.5.22.联机测试
-
1.6.5.33.联机显示
-
1.6.6思考题
-
1.6.7附 录
-
1.6.7.11.最小二乘法
-
1.6.7.22.多电子原子的电子排布
-
1.7实验七 液晶电光效应综合实验
-
1.7.1背景知识
-
1.7.2实验原理
-
1.7.2.11.液晶光开关的工作原理
-
1.7.2.22.液晶光开关的电光特性
-
1.7.2.33.液晶光开关的时间响应特性
-
1.7.2.44.液晶的视角特性
-
1.7.2.55.液晶光开关构成图像显示矩阵的方法
-
1.7.3仪器介绍
-
1.7.4实验内容及步骤
-
1.7.4.11.准备工作
-
1.7.4.22.液晶电光特性测量
-
1.7.4.33.液晶的时间响应的测量
-
1.7.4.44.液晶光开关视角特性的测量
-
1.7.4.55.液晶显示器显示原理观测
-
1.7.5思考题
-
1.7.6注意事项
-
1.7.7附 录
-
1.7.7.11.数字荧光示波器简介
-
1.7.7.22.数字存储示波器与计算机通讯
-
1.8实验八 空气热机实验
-
1.8.1背景知识
-
1.8.2实验原理
-
1.8.3仪器介绍
-
1.8.3.11.空气热机实验仪器连接图
-
1.8.3.22.空气热机实验仪
-
1.8.3.33.电加热器电源
-
1.8.3.44.空气热机测试仪
-
1.8.3.55.空气热机实验通信器
-
1.8.3.66.力矩计
-
1.8.4实验内容及步骤
-
1.8.4.11.验证卡诺定理
-
1.8.4.22.测量热机输出功率、输出效率与负载的关系
-
1.8.5思考题
-
1.8.6注意事项
-
1.8.7附 录
-
1.8.7.11.实测数据示例
-
1.8.7.22.软件操作说明书
-
1.9优秀实验论文之一 光学多通道线性定标选点对光谱测量精确度影响
-
1.9.10 引言
-
1.9.21 实验设备及原理
-
1.9.32 实验设计及步骤
-
1.9.43 数据处理
-
1.9.54 分析及结论
-
1.10优秀实验论文之二 太阳能电池最大输出功率随光照强度的变化
-
1.10.10 引言
-
1.10.21 实验原理
-
1.10.32 实验结果及分析讨论
-
1.10.43 结论
-
1.11优秀实验论文之三 夫兰克-赫兹实验曲线波谷趋势异常分析
-
1.11.10 引言
-
1.11.21 夫兰克-赫兹实验原理
-
1.11.32 不同拒斥电压下的伏安特性曲线
-
1.11.43 分析与讨论
-
1.11.54 结论
-
1.12附表1 我国法定计量单位和国际单位制
-
1.13附表2 物理常量表
-
1.14附表3 物理密度表
-
1.15附表4 海平面上不同纬度处的重力加速度
-
1.16附表5 固体的线[膨]胀系数
-
1.17附表6 在20℃时某些金属的弹性模量
-
1.18附表7 在不同温度下与空气接触的水的表面张力系数
-
1.19附表8 粘滞系数
-
1.20附表9 固体导热系数
-
1.21附表10 某些固体和液体的比热容
-
1.22附表11 常用光源的谱线波长表
-
1.23附表12 不同温度下干燥空气中的声速
-
1.24参考文献
1
大学物理综合设计实验