-
1.1同济二附中理工特色校本教材丛书
-
1.2序
-
1.3前 言
-
1.4第一章 绪论
-
1.4.11.1 基因是什么?
-
1.4.21.2 我们的基因从哪里来?
-
1.4.31.3 基因是怎么控制人体的?
-
1.5第二章 基因的分类与特点
-
1.5.12.1 基因分类
-
1.5.22.2 基因特点
-
1.5.32.3 实践操作
-
1.6第三章 基因的表达与调控
-
1.6.13.1 基因表达
-
1.6.23.2 基因表达调控
-
1.6.33.3 实践操作
-
1.7第四章 基因的遗传与变异
-
1.7.14.1 遗传与变异
-
1.7.24.2 遗传与变异的关系
-
1.7.34.3 实践操作
-
1.8第五章 基因的修饰与改造
-
1.8.15.1 基因修饰
-
1.8.25.2 基因改造
-
1.8.35.3 实践操作
-
1.9第六章 基因的识别与检测
-
1.9.16.1 基因识别
-
1.9.26.2 基因检测
-
1.9.36.3 实践操作
-
1.10第七章 基因的应用领域
-
1.10.17.1 生产领域
-
1.10.27.2 军事领域
-
1.10.37.3 环境保护
-
1.10.47.4 医疗方面
-
1.10.57.5 基因工程药物
-
1.10.67.6 农作物培育
-
1.10.77.7 基因与健康
-
1.10.87.8 分子进化研究
-
1.11第八章 附录
-
1.11.18.1 生物学实验室安全须知
-
1.11.28.2 生物学实验室通则
-
1.11.38.3 常用仪器的基本使用方法和注意事项
-
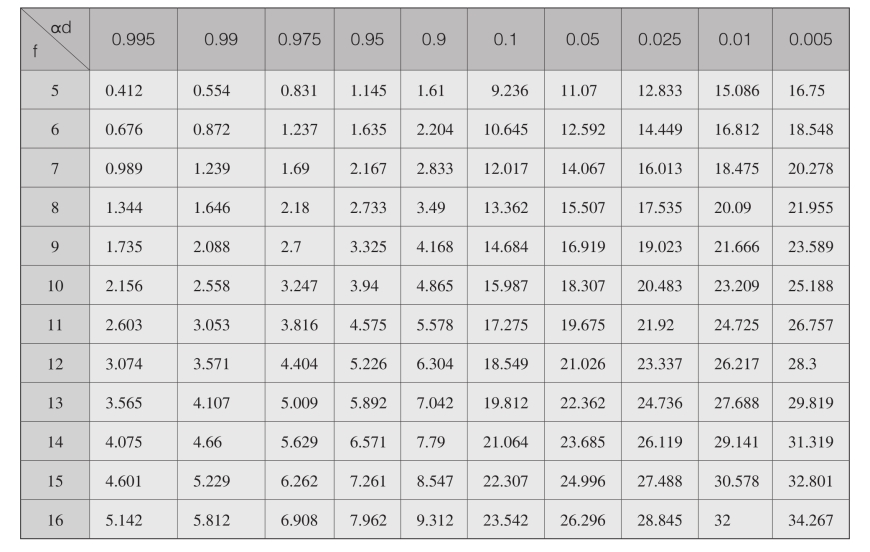
1.11.48.4 卡平方(x2)测验
-
1.11.58.5 实验室常用数据
-
1.11.68.6 研究案例
-
1.12参考资料
1
基因探秘

 (O-E)
(O-E) (O-E)
(O-E)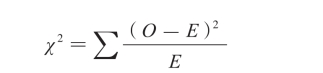
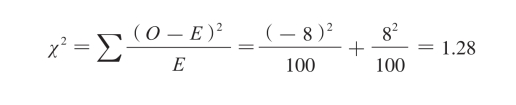
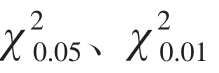 较:若
较:若 P>0.05,表明实际观察次数与理论次数差异不显著,可以认为实际观察的属性类别分配符合已知属性类别分配的理论或学说;若
P>0.05,表明实际观察次数与理论次数差异不显著,可以认为实际观察的属性类别分配符合已知属性类别分配的理论或学说;若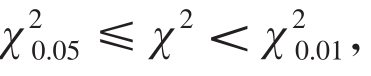 0.01<P≤0.05,表明实际观察次数与理论次数差异显著,可以认为实际观察的属性类别分配不符合已知属性类别分配的理论或学说;若
0.01<P≤0.05,表明实际观察次数与理论次数差异显著,可以认为实际观察的属性类别分配不符合已知属性类别分配的理论或学说;若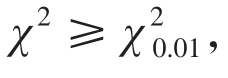 P≤0.01,表明实际观察次数与理论次数差异极显著,可以认为实际观察的属性类别分配极显著地不符合已知属性类别分配的理论或学说。
P≤0.01,表明实际观察次数与理论次数差异极显著,可以认为实际观察的属性类别分配极显著地不符合已知属性类别分配的理论或学说。

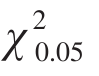 =7.815,因x
=7.815,因x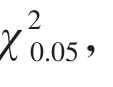 P<0.05,所以应否定H
P<0.05,所以应否定H