四、回眸历史，利玛窦功不可没

利玛窦在中国首先以传播西方数学拉开了传播天主教的帷幕，同时也将中国的儒家文化传向欧洲，开启了中西文化交流的大门。那么，利玛窦到底给中国带来了哪些西方数学和科学文化，同时向欧洲输送了哪些文化思想呢？

1．系统引入西方数学理论和计算技术

从14世纪开始，欧洲大陆进入文艺复兴时期。“文艺复兴运动”始于意大利的佛罗伦萨，后延伸到罗马、米兰、威尼斯等城市，以后又扩展到德国、法国、英国、荷兰等欧洲其他国家。

这是一场在文学、艺术和科学文化等方面开展的轰轰烈烈的运动，旨在反对中世纪的黑暗统治，提倡人性自由和崇尚科学，代表着新的人文主义思想。

在利玛窦生活的那个年代，世界数学尚处于由初等数学向变量数学过渡的时期。12世纪，古希腊数学家丟番图的《算术》和阿拉伯数学家花拉子米的《代数学》已通过北非传到了欧洲，促成了斐波那契《算经》的问世。⁽²⁸⁾同时，欧几里得的《几何原本》首次被译成拉丁文，在欧洲重现了它的风采。三角学由于航海、历法和天文观测的需要，得到了进一步的发展。

到了15世纪，欧洲数学开始全面复苏。1545年，意大利学者卡尔达诺出版了《大术》一书，给出了三次和四次代数方程的一般解法，并用几何方法证明了其解法的正确性；1572年，意大利的邦贝利在他出版的《代数学》中引入了虚数，完全解决了三次代数方程的不可约问题，使得代数方程的求解成为16世纪欧洲的主流。1482年，拉丁文《几何原本》首次被印刷出版；1574年，克拉维乌斯在罗马出版的欧几里得《几何原本》（拉丁文版本）15卷，对中国数学产生了巨大影响。

此外，绘画和制图刺激了透视学的兴起，从而诞生了射影几何学。而制图学的产生，使得欧洲绘制出首张世界地图（1569年）。此时的三角学也已经由球面三角学转向平面三角学，使三角学成为纯粹数学的一个独立分支。⁽²⁹⁾因此，利玛窦以几何学为重点，兼及三角学与代数学，向中国推介了西方近代初等数学。⁽³⁰⁾

利玛窦最成功地给中国人传播的西方数学便是欧几里得的《几何原本》。在翻译《几何原本》之前，利玛窦就认为：

中国人的数学属于实用型，他们提出了各种各样的命题，却都不证明。这种数学只有结果而没有证明过程，永远不能成为理论体系。而欧几里得则与之相反，将命题依次提出，而且如此确切地加以证明，即使最固执的人也无法否认它们。⁽³¹⁾

《几何原本》不仅仅是西方经典的演绎数学理论著作，它的意义更主要体现在思维方法方面。徐光启就正确地指出：

此书为益，能令学理者祛其浮气，练其精心；学事者资其定法，发其巧思，故举世无一人不当学。能精此书者，无一事不可精；好学此书者，无一事不可学。⁽³²⁾

在翻译《几何原本》的过程中，由利玛窦口述，徐光启记录下来加以整理。由于《几何原本》与我国古代传统的数学截然不同，加上徐光启又不懂拉丁文，许多译名都是从无到有、边译边创造。徐光启借用我国古代用语，并从词义、音译及概念本身考虑，精心研究，多方揣摩，煞费苦心，使译文通俗易懂、错误很少。许多译名十分贴切，不但在我国沿用至今，并且还影响了日本、朝鲜等国。

“几何”一词，现已成为数学中的一个专有名词和重要分支，但欧几里得《几何原本》中并没有这个词，当时是由利玛窦、徐光启在翻译时加上去的。利玛窦、徐光启为什么会用“几何”一词作译名众说纷纭。据传徐光启考虑用“行学”这个名词，后来觉得不好，才又从发音、原意考虑，一连想了十多个音似的汉字，都不十分贴切。

后来，他从一句古诗“河汉清且浅，相去复几许”中的“几许”联想到“几何”，于是创造性地译为《几何原本》。至于徐光启怎么会由“几许”想到“几何”，一般认为这是由于“几何”是拉丁文geometria中“geo”的音译，且又含有数学上的“多少”的意思。⁽³³⁾

徐光启在翻译《几何原本》时，看到了西方科学对基础研究和科学推理的重视，认为数学是其他一切学科的基础，并指出学习数学无所不通，其关系在于“理不明不能立法，义不明不能著数，明理辨义，推究颇难，法立数著，遵循甚易”。他在《条议历法修正岁差疏》中提出了著名的“度数旁通十事”⁽³⁴⁾：

其一，历象既正，除天文一家言灾祥祸福、律例所禁外，若考求七政行度情性，下合地宜，则一切晴雨水旱，可以约略预知，修救修备，于民生财计大有利益。

其二，度数既明，可以测量水地，一切疏浚河渠，筑治堤岸、灌溉田亩，动无失策，有益民事。

其三，度数与乐律相通，明于度数即能考正音律，制造器具，于修定雅乐可以相资。

其四，兵家营阵器械及筑治城台池隍等，皆须度数为用，精于其法，有裨边计。

其五，算学久废，官司计会多委任胥吏，钱谷之司关系尤大。度数既明，凡九章诸术，皆有简当捷要之法，习业甚易，理财之臣尤所亟须。

其六，营建屋宇桥梁，明于度数者力省功倍，且经度坚固，千万年不圮不坏。

其七，精于度数者能造作机器，力小任重，及风水轮盘诸事以治水用水，凡一切器具，皆有便利之法，以兹民用，以利民生。

其八，天下舆地，其南北东西纵横相距，纡直广袤。及山海原隰，高深广远，皆可用法测量，道理尺寸，悉无谬误。

其九，医药之家，宜审运气；历数既明，可以察知日月五星躔次，与病体相视乖和逆顺，因而药石针砭，不致差误，大为生民利益。

其十，造作钟漏以知时刻分秒，若日月星晷，不论公私处所、南北东西、欹斜坳突，皆可安置施用，使人人能分更分漏，以率作兴事，屡省考成。

后来，徐光启又写了《几何原本杂议》，并且根据利玛窦的口述翻译整理了《测量法义》，自己撰写了《测量异同》《勾股义》。他用这些著作的基本定理来解释和补充中国传统测量法中的“义”，使中国古代数学更具应用性、条理性和系统性。

从《几何原本》到《勾股义》，徐光启把中国的传统数学向前推进了一大步，开创了翻译和介绍西方数学及其他科学的新风气。《几何原本》的翻译出版掀起了中国数学家学习西方数学的高潮，这对当时中国学术界产生的冲击力是巨大的和不可磨灭的。

继徐光启之后，清朝时期数学界的代表人物是梅文鼎（1633—1721年）。他精通中西数学，对发展中国传统数学和传播西方数学均做出了重大贡献。

梅文鼎以毕生精力专攻天文学和数学，他尽量消化、彻底理解从西方输入的新方法，对清代中期数学研究再现高潮有积极影响。他一生都在整理、研究中国传统数学和注解、介绍、吸收西方数学，并且著书立说约70多种，如《算要》3卷、《平三角举要》5卷、《弧三角举要》5卷等（在第七章有详细介绍）。

清朝末期，李善兰和伟烈亚力合作翻译了《几何原本》后9卷；李子金著《算学通义》5卷、《几何简易集》4卷、《元弧象限表》；还有一些著作也受到几何学思维方式的影响，使得欧氏几何学成为中国近代数学的一个新的数学分支和发展方向。

400多年前，徐光启就倡导人们学习《几何原本》，极力主张用严谨的逻辑推理方式取代束缚人们思想且形式死板的八股制，他明确而系统地阐述了数学与其他科学技术的密切关系，从理论上对数学的应用加以高度的概括，对中国数学的发展在思想方法上起到了一定的指导作用。

如今，人们已经很难发现《几何原本》的诞生有什么了不起的地方。那么，晚清的梁启超说此书“字字精金美玉，为千古不朽之学问”是否刻意夸大其词呢？中国在缺乏几何系统知识的前提下，实现了世界历史上一度罕见的繁荣，好像对传统社会中齐家治国平天下的观念来说，几何的用处似乎不是太大。徐光启对此的回答是：“无用之用，众用所基。”这就是《几何原本》的精髓，也是基础学科普遍适用的原理。

谈起欧几里得几何学公理体系，人们都会认为它应用于自然科学技术领域，却很少有人想到将它用于社会制度的改革之上。⁽³⁵⁾

1980年，朱维铮教授发现了康有为的已经被人遗忘的著作《实理公法全书》。众所周知，以“托古改制”著称的康有为一生表述其政治思想时，总追根寻源到《礼记·礼运篇》。但朱维铮教授的研究却表明：《实理公法全书》的思路却是依据《几何原本》而来。

康有为将《几何原本》的公理体系一路推衍至社会政治领域，在《实理公法全书》中发表了自己关于未来的理想社会的蓝图，可是很少有人把康有为的思想和他的政治活动与300年前的《几何原本》联系起来。

中国历史与欧氏几何的某种关联，并不是数学中的几何知识的具体应用，而是几何学中隐含着的人们认识宇宙的“世界观”。或许，只有徐光启的“无用之用，众用所基”能够提供一些合理的解释吧。

2．非欧几何继而进入大陆

除欧几里得的《几何原本》外，利玛窦也通过各种形式传入了当时流行于欧洲的非欧几何知识，主要有圆锥曲线、平行正投影、球极投影、画法几何和透视法等。

关于平行正投影在我国古代曾经有人研究过，如北宋时期的著名画家、建筑学家李诫在他的《营造法式》（1103年）中就有不少图形的绘制采用了正投影的方法；明朝万历年间出现的《鲁班经》中也有很多正投影图形知识的应用⁽³⁶⁾。但是中国古代的平行正投影似乎都没有研究过球面，就是曾经研究过的立方体（如房屋、石头等），也没有具体的绘制方法，即没有使用精确的几何方法绘制。

圆锥曲线是古希腊数学家和天文学家的一项重要发现，备受人们的赞誉，在中世纪之前就被广泛地应用到很多领域。欧洲学者几乎都了解这种曲线，熟悉它的性质。利玛窦来到中国后，最早传入的几何知识就是圆锥曲线。

1584年4月，利玛窦在肇庆给国人展示了一幅从意大利带来的世界地图。这幅地图非常精美，顿时吸引了不少人来观看。利玛窦应肇庆知府王泮之请，于同年11月份给他另绘制了一幅著名的《山海舆地全图》。

1596年11月，利玛窦在南昌收到了他的老师克拉维乌斯于1593年出版的新书《论星盘》。这是一本介绍星盘制作的著作，其中包含了大量圆锥曲线的内容并且运用了数学知识阐述其原理。星盘的具体做法都是在圆锥曲线知识的基础上一步步严格推理出来的，而且除了需要欧氏几何和圆锥曲线知识以外，还需要球极投影的知识，球极投影是制作星盘的关键。所以，学习星盘制作还必须学习球极投影。

1601年7月，利玛窦在北京与李之藻相识。李之藻（1564—1630年），字振之，一字我存，号凉庵居士，又号凉庵逸民，浙江杭州人。他是个地图绘制爱好者，20岁的时候曾自己搜集资料，亲自绘制过一幅全国地图。李之藻看过利玛窦的世界地图后，对其绘制地图的精美和精确程度感到异常惊讶。

1602年，李之藻开始跟利玛窦学习地理学、地图学、绘制世界地图技艺、天文学和数学，且尤其偏爱数学。他将利玛窦绘制的《山海舆地全图》放大后重新印刷，这就是著名的《坤舆万国全图》。

这幅地图最初的底本来自罗马，采用的是当时欧洲比较流行的投影画法——椭圆投影，其特点就是将整个地球表面的投影图绘制成一个标准的椭圆。圆锥曲线在中国古代没有人研究过，它现在应用于地图制作完全得益于利玛窦的工作。

李之藻掌握了几何学的大部分内容，学会并且制作了一具星盘，它运转极其精确。李之藻绘制的数学图形可以和任何欧洲学者所绘制的图形相匹敌。1607年，他出版了论星盘的著作《浑盖通宪图说》，利玛窦将它作为中国人完成的第一部数学和天文学著作，赠送给罗马的耶稣会会长和克拉维乌斯教授（利玛窦的恩师）。在这本书的序言中，李之藻说：

昔从京师识利先生，欧逻巴人也。示我平仪，其制约浑，为之刻画重固，上天下地，周罗星程，背结规筒貌则盖天，而其度仍从浑出。取中央为北权，合《素问》中北外南之观；列三规为岁候，邃义和侯星寅日之旨，得未曾有，耳受手书，颇亦镜其大凡。旋奉使闽之命，往返万里，测验无爽，不揣为之图说，间亦出其鄙谢，会通一二，以革中历。

由此可见，利玛窦给李之藻讲解了球极投影，并教会了他星盘的制作和使用方法。

1608年，李之藻又著成了《圜容较义》一书。他在此书的序言中讲：“昔从利公研穷天体，因论圜容，拈出一义，次为五界十八题。”可见此书直接来源于利玛窦。此书分为十八个命题，分别讲述了多边形的面积问题、锥体的体积问题、圆内接多边形和外切多边形问题、球内切多面体问题等。这些都是利玛窦与徐光启翻译的《几何原本》中没有的内容，此书的第十八题证明了“凡浑圆形与圆外角形等周者，浑圆形必大于圆角形”，即“表面积一定的球和旋转体相比，前者体积大”。

为了证明这个命题，李之藻使用了椭圆曲线并且多次借用古希腊数学家阿基米德（Archimedes，前287—前212年）《圜书》中的命题结论。阿基米德的《圜书》是一本讨论圆的面积和体积的书，里面包含了椭圆面积的求法。

此后，李之藻给出了黄道的天顶规的画法、地平规的画法、地平渐升度的画法、朦胧影的画法、黄道的画法、黄道十二宫分点的画法、黄道经线的画法、黄极和赤道南北极的画法、有各种坐标的恒星的画法等。因此可以推定，利玛窦给李之藻讲解了球极投影、圆锥曲线的知识和西方早期的画法几何，并教会了他星盘的制作和使用方法。

3．介绍西方油画和透视法

利玛窦到中国以后，在给国人展示的物品中，也多次提到西方绘画如圣母像、耶稣像等。这些绘画有的是从印度、澳门、日本等地转赠来的，也有利玛窦自己绘制的。利玛窦在罗马学院曾学习了三个月的透视学，因此，他非常熟悉当时在欧洲兴起的油画透视画法，了解其中的数学投影原理，并且将这种绘画技法带到了中国，在绘画的时候采用了透视法。

在欧洲文艺复兴时期产生的透视学与透视画法的技巧理论，是“文艺复兴运动”的杰出成果和最著名的发现。应用透视学的理论和方法不仅使绘画风格和形式多样化，而且也发展和丰富了以后的工程设计的表现手段，能客观地表现出设计后的视觉效果。绘制设计效果图时，如果不懂得透视画法的技巧理论，可能无法达到所需要的效果。

透视画法方面的突出代表就是德国绘画大师阿尔布雷特·丢勒（Albrecht Dürer，1471—1528年）。同绘画大师达·芬奇一样，丢勒也具有科学的头脑，他曾经深入研究数学和透视学，并写下了大量笔记和论著。利用透视法和人体解剖学方法创作了许多反映社会现实的绘画作品。

因此，丢勒不仅是画家，而且是数学家、机械师、建筑学家，也是欧洲文艺复兴时期“透视学画派”的领军人物。

据记载，1602年，利玛窦曾奉万历皇帝的命令，耗时三天绘制成《西方宫廷生活图》，并且在晚年也曾绘制过《野墅平林图》。从现存于辽宁省博物馆的《野墅平林图》中我们可以看出，这幅写实油画并不是中国式的写意画法，整幅画作远近分明、明暗比例协调、视野开阔，显然是采用了西方透视画法。

此画是否出自利玛窦之手，目前仍存在争议。最早时，此幅绘画作品曾被认为是荷兰人格洛特所作，不过后来经北京二友山房装裱时，发现画的背面角绢与托纸处有模糊字迹，加上各种资料旁证，才确定为利玛窦所绘制，据说此画是用来装饰北京教堂的祭坛的⁽³⁷⁾。

1601年，利玛窦在给万历皇帝的贡品中有一幅圣母像，献给皇帝之前，他曾给很多人展示过，还对比中国画，对西方画法进行了评价，他说：

中国画但画阳不画阴，故看之人面躯正平，无凹凸相；吾国之画兼阴与阳写之，故面有高下，而手臂皆轮圆耳。凡人之面正迎阳，则皆明而白；若则立，则向明一边者白，其不向明一边者，眼、耳、鼻、口凹处，皆有暗相。吾国之写像者，解此法用之，故能使画像与生人亡异也。⁽³⁸⁾

在《译〈几何原本〉引》中，利玛窦又写道：

察目视势，以远近正邪高下之差，照物状可画立圜立方之度数于平版之上，可远测物度及真形；画小，使目视大；画近，使目视远；画圜，使目视球，画像有坳突；画室屋有明暗也。⁽³⁹⁾

在所有向利玛窦学习西方绘画的中国人中，成就最高的当数游文辉了。游文辉（Manuel Pereira，字含朴）是澳门人，他1575年出生，1593—1598年在日本接受天主教文化，回国后追随利玛窦学习西方绘画和从事绘画活动。游文辉留下来的作品并不多，最著名的是1610年利玛窦去世之后他绘制的利玛窦像。

这是一幅标准的西方肖像画，构图既饱满又简练，显示出相当高的艺术概括能力。该画对明暗的处理也很有特色，光线从画面左上方射去，在眼眶、鼻梁、面颊的暗面投下了丰富的阴影，尤其在白色衣领上的投影可以使人明显感受到强烈的光源。

17世纪的中国人能将油画肖像绘至这样的水平，的确是件非常不容易的事情。由此可以看出，利玛窦一定给游文辉讲解过西方绘画的原理和其中的数学理论以及西方的透视法。

清朝初期，在华的耶稣会士利类思（Lodovico Buglio，1606—1682年）、南怀仁（Ferdinand Verbiest，1623—1688年）、郎世宁（Giuseppe Castiglione，1688—1766年）等人纷纷作画，使西洋画在中国风靡一时。西洋画家郎世宁与工部侍郎、数学家年希尧（1671—1739年，字允恭）合著《视学》，系统地介绍西方透视法的知识和技术，使中国美术出现了中西结合的绘画风格⁽⁴⁰⁾。

《视学》一书初刻于雍正七年（1729年），1735年再版。而直到1798年，法国数学家蒙日（Gaspard Monge，1746—1818年，被誉为画法几何学奠基人）才出版了《画法几何学》。如此看来，年希尧的《视学》比蒙日的《画法几何学》早了60多年。

《视学》也是一部数学著作，它图文并茂，阐述透视学原理。全书用了很大的篇幅介绍透视学中的基本问题和基本方法，包括技法方面的量点法和截距法、透视角度的平行透视和成角透视、视平线位置方面的仰望透视法以及轴测图上中心光源阴影的处理等。

在图例方面，年希尧对一般立体图形均用二视图表示尺寸及形状，再作底面次透视图，以便决定各特征点之高度，最后才把整体透视图画出来。书中所使用的术语，有的沿用至今，如“地平线”“视平线”等。

总而言之，利玛窦传播的这些非欧几何（主要是透视法）知识，直接被应用到了科学技术活动中，特别是天文观测、地理勘测、地图绘制以及绘画艺术中，有力地促进了当时中国科学技术的发展。

4．推介西方测量术和三角学

此外，利玛窦与李之藻合译的《同文算指》（译自克拉维乌斯的《实用算术概论》，1614年版）是明清之际一部十分重要的数学著作，它参考了中国明代数学家程大位的《算法统宗》一书进行编译，分为“前编”2卷、“通编”8卷和“别编”1卷三个部分。该书全面介绍了西方的笔算方法以及算术方面的成果，其中介绍的计算方式与现代笔算方法非常接近，内容有整数和分数的四则运算，比例、分数、级数和开方等算法⁽⁴¹⁾。

与希腊数学相比，古代的中国数学表现出强烈的算法精神，在算法方面也取得了突出的成绩以及杰出的建树，如《孙子算经》《周髀算经》和《九章算术》等著作都含有大量的算法。《同文算指》不仅代表了西方的数学水平，也体现了中国古代数学的算法精神。作为第一部从西方翻译过来的系统介绍欧洲算法的数学书，其贡献与影响有目共睹，它所介绍的“验算方法”也是中国前所未有的。他们合译的另一本著作《圜容较义》（1608年）主要介绍比较图形关系的几何学知识，在当时也颇具影响力。

1607年，利玛窦与徐光启合译了《测量法义》（1608年定稿），全面介绍了欧洲几何测量方法，该书可以被认为是《几何原本》中的几何学理论在实践中的应用。

之后，徐光启根据传统的测量方法，撰成《测量异同》和《勾股义》（1609年）⁽⁴²⁾。1631年，徐光启与罗雅谷合作出版了《测量全义》，这是西方三角学以及测量术输入中国之始⁽⁴³⁾。

5．西方天文学、地理学和制图学

在天文学方面，继利玛窦1605年著《乾坤体义》一书后，熊三拔与徐光启合著《简平仪说》，周子愚、卓尔康合著《表度说》，阳玛诺著《天问略》，汤若望先后著《古今交食考》《西洋历则》《星图》《八线表》《赤道南北两动星图》等天文著作，系统地向中国传播西方天文学的知识；南怀仁制造了黄道经纬仪、赤道经纬仪、地平经纬仪、天体仪等天文仪器，并著《灵台仪象志》16卷。

《灵台仪象志》内容相当广泛，几乎涉及了当时天文观测工作的所有方面。首先，南怀仁在书中介绍了西方近代天文仪器的制作方法、安装方法和使用方法，以及在仪器制作过程中对部件强度的要求、材料的选用、基座的设计、制作中使用的工具及其使用方法等。

其次，南怀仁还针对实用测量问题，如高度或远近的测量方法、经纬度差与地面距离的换算办法，以及纬线长度的计算等也做了较清楚的解说。《灵台仪象志》中还介绍了一些西方科学知识，如重心、比重等概念；温度、湿度的测量方法；蒙气差改正的求法；杠杆、滑轮等简单机械；单摆与自由落体定律；光的折射和颜色的合成；地球半径测量法等。

最后，书中还给出包含1876颗恒星位置的星表，并且附有许多计算用表，如蒙气差计算表、以高测远表、以远测高表、地面上两地点的角距离与相距里数的换算表等。《灵台仪象志》为观测天文数据提供了重要的参考资料⁽⁴⁴⁾，对明末清初我国天文学的发展具有重要的意义。

清朝学者阮元在《畴人传》“南怀仁”篇中称赞道：“西人熟于几何，故所制仪象极为精审，盖仪象精审，则测量真确，测量真确则推步密合。西法之有验于天，实仪象有以先之也。”⁽⁴⁵⁾

在地理学和制图学方面，利玛窦于1584年在肇庆首次绘制中文版的《山海舆地全图》，激起了中国知识分子了解世界的热情。之后，国人对传播地理知识和收藏《世界地图》的兴趣持续高涨。

1602年，李之藻又在北京修改并绘制了《坤舆万国全图》，其中所测定的经纬度与现在的数据基本一致；庞迪我也绘制了《海外舆图全说》。

1623年，艾儒略（Julio Aleni，1582—1649年）著《职方外纪》6卷，其中附有7幅地图：《万国全图》《北舆全图》《南舆全图》《亚细亚图》《欧罗巴图》《利未亚图》《南北阿墨利加图》。

1674年，南怀仁著《坤舆全图》《坤舆图说》；蒋友仁（MichaelBenoist，1715—1774年）增补了《坤舆全图》《乾隆皇舆全图》等地理图，详细地叙述了各国的地理、物产、气候、风土、民情和地质地貌，成为中国近代地图学的肇始。

利玛窦除了通过翻译数学著作来传播西方数学外，他的另一个贡献就是多次请求罗马教廷向中国派遣精通数学和天文学的传教士。通过他的努力，邓玉函（Joannes Terrentius，1576—1630年）、汤若望（Joannes Adam Schall von Bell，1592—1662年）、罗雅谷（Jacobus Rho，1593—1638年）、艾儒略（1582—1649年）等西方科学家先后来到中国，对我国的数学及科学教育做出了巨大贡献，也培养和影响了大批数学人才。

例如：1623年，艾儒略的《西学凡》介绍了教会学校的6个基本学科（文科、理科、医科、法科、教科、道科）；1631年，邓玉函的《大测》是第一部系统介绍欧洲三角学内容的中文著作。

明末清初，中国学者受到利玛窦的影响，各种有关西法之数学著作如《太西要算》（明孙元化撰）、《中西数学图说》（明李笃培撰）、《天学会通》（明薛风怍著）、《历算全书》（清梅文鼎著）、《割圜八线表》（明黄宗羲作）、《赤水遗珍》（梅成著）、《杜式九术全本》（张冠著）、《续增新法比例》（陈厚耀著）等犹如雨后春笋，相继问世⁽⁴⁶⁾。这几部著作对后来中国数学的发展都有重要的影响，对现在的数学研究仍具有重要意义。

事实上，利玛窦虽然没有创造出属于自己的数学原理和数学方法，但他借“学术传教”策略而热心传播西方数学文化，其价值已经不再局限于一些数学成果，而是一种中国在封建社会制度下迫切需要的创新精神。从这种意义上来说，利玛窦是一个出色的数学教育家，他对中国数学教育的影响是长久和深远的。

6．向欧洲输送华夏文化

利玛窦为了传教的需要，不得已采用“学术传教”策略，将西方数学传到中国，然而起初他对中国的传统数学并不欣赏和重视。当时中国的传统数学主要是算术，计算工具是算盘。他认为：“中国人的算术不过是以串在绳子上的珠子构成的一个工具进行运算的，这个方法虽然可靠，但容易犯错，可以说比起欧洲的算术来说是微不足道的。”⁽⁴⁷⁾

因此，利玛窦最初传播西方数学时，主要目的是想提高“天主”的威望，震慑并且打压中国人的自信心。随着时间的推移，利玛窦逐渐发现了中国古代哲学中蕴藏着宝贵的精神财富，这就使得利玛窦等传教士开始向西方传输中国古代典籍著作中的儒家学说、数学思想和数学方法。

利玛窦创造的“数学文化传播”模式得到了其后的德国数学家莱布尼茨（G．W．Leibniz，1646—1716年）的认同，并且莱布尼茨也赞成在中国的古籍中寻找隐藏着的智慧的火花⁽⁴⁸⁾。突出的例子便是中国古籍《易经》中的“象数主义”思想以及“乾卦”方法对莱布尼茨的“二进制”理论的影响和有益补充。

（1）二进制与易经八卦图。

《易经》（也称《周易》或《易》）是一部中国古哲学书籍，是中国传统思想文化中自然哲学与伦理实践的根源，是华夏五千年智慧与文化的结晶，被誉为“群经之首，大道之源”。

《易经》是建立在阴阳二元论基础上对事物运行规律加以论证和描述的书籍，其对天地万物进行性状归类，提出天干地支五行论，甚至精确到可以对事物的未来发展做出较为准确的预测。

据说《易经》是由伏羲氏与周文王（姬昌）根据《河图》《洛书》演绎并加以总结概括而来（同时产生了易经八卦图）。

利玛窦在中国传教期间，曾经对《易经》中的八卦原理进行了详细研究，著有《八卦与九宫之变化》一书。利玛窦去世之后，又有其他的耶稣会士热衷于《易经》的研究，并且将有关的著作在欧洲出版。

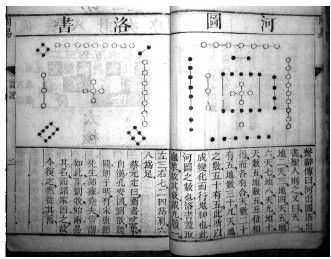《周易》	《河图》《洛书》

伏羲氏像	周文王（姬昌）像

1658年，耶稣会士卫匡国（M．Martinius，1614—1661年）在德国慕尼黑出版了《中国上古史》（另译《中国历史十卷》《中国先秦史》或《中国历史概要》），首先定义了阴、阳的概念，详细介绍了太极八卦——“阴阳生两仪、两仪生四象、四象生八卦”的演化过程，并且给出了伏羲六十四卦图谱。现在的史料认为，卫匡国的《中国上古史》第一次向欧洲传播了《易经》和周文王六十四卦图⁽⁴⁹⁾。

1660年，德国著名神学家斯比塞尔（G．Spizel，1639—1691年）在荷兰莱顿出版了《中国文史评析》，书中记载了《易经》，并且首次称《易经》为二进制。这里要特别说明，《中国文史评析》一书的主要参考文献就是金尼阁的《利玛窦中国札记》以及卫匡国的《中国上古史》。

1664年，耶稣会士柏应理（P．Couplet，1623—1693年）在中国传教期间，完成了著作《中国哲学家孔子》（或译为《中国哲学家之王》），并将它翻译成了拉丁文，1687年在法国巴黎出版。这部书中有13页介绍了《易经》内容，不仅包含伏羲八卦次序图和伏羲八卦方位图，还有周文王六十四卦图，并且在这些图中均第一次标上了阿拉伯数字1、2、3、4、5、6、7、8直至64⁽⁵⁰⁾。

据史料记载，早在1666—1667年间，莱布尼茨在纽伦堡学习时已经开始研究中国古典哲学，他先后拜读了斯比塞尔的《中国文史评析》和柏应理的《中国哲学家孔子》这两部著作。1687年12月19日，莱布尼茨在致友人冯·黑森·莱茵费尔的信中说自己阅读了《中国哲学家孔子》这本书。而在这封信中，还出现了“Fohi”的字样，这个词译为中文就是“伏羲”⁽⁵¹⁾。这就是说，莱布尼茨当年应该见过伏羲八卦次序图、伏羲八卦方位图及周文王六十四卦图。

莱布尼茨的有关“二进制”的论文最早写于1679年3月15日。那时他用拉丁文撰写了题为“二进制算术”的论文手稿，对二进制进行了充分的讨论，并建立了二进制下的用“0”和“1”表示一切数的方法以及数字之间的加、减、乘、除四则运算规则，同时列出了数表。可惜，莱布尼茨的这篇论文没有发表，可能他还没有看出来二进制有什么实际应用⁽⁵²⁾。

1697年，莱布尼茨在《新年信》中才首次论及这一发现。这一年，莱布尼茨结识了在中国传教的白晋神父（J．Bouvet，1656—1730年）。1701年2月15日，莱布尼茨将发现二进制之事写信给白晋，并建议将二进制的算法呈献给喜爱数学的中国康熙皇帝。同年2月26日，莱布尼茨将他的二进制论文呈交巴黎科学院，然而科学院秘书长封丹内（D．Fontenelle）于4月30日以“无法理解，看不出二进制有什么用处”为由拒绝接收和发表。

1701年11月4日，白晋致函莱布尼茨，告诉他二进制早已经隐含在中国古代《易经》的伏羲六十四卦图中了。1703年4月1日，莱布尼茨收到了白晋寄来的一部《易经》以及有关邵雍六十四卦象的信件。

莱布尼茨看到《易经》以及六十四卦象后非常高兴，他对中国古代的易家学说中的“八卦六十四爻”大为赞赏，并为其发明的“二进制理论”找到了应用领域。此时，他可以向巴黎科学院的秘书长证明他的二进制的用处了，莱布尼茨甚至在八卦中看到了创世的模型和以这种方式写成的安息日符号以及“三位一体”。

1703年5月5日，莱布尼茨撰写了《二进制算术的阐述——关于只用0与1兼论其用处以及伏羲氏所用数字的意义》，发表在法国《皇家科学院院刊》上⁽⁵³⁾。

莱布尼茨从二进制理论和六十四卦象的相同之处，感受到了中国人的祖先实际上是非常英明的。至于为什么莱布尼茨没有从斯比塞尔的《中国文史评析》和柏应理的《中国哲学家孔子》这两部著作中发现二进制的用处，至今仍然是一个谜。

不过，莱布尼茨在1716年临终前未写完的《中国自然神学论》中，诚实地表示由伏羲的图像（八卦先天图）可以证明，易经的六十四卦中包含了二进制⁽⁵⁴⁾，他的二进制思想源于中国古代的《易经》以及伏羲六十四卦图。

从这些论述中可以看出，《易经》中透析出来的中国古代数学思想及成就深深吸引了莱布尼茨，特别是《易经》，为他的二进制理论找到了诠释和应用的依据。白晋也曾高度评价说，《易经》中的数字系统可以和毕达哥拉斯以及柏拉图的数字系统媲美，伏羲将一切科学隐藏到了《易经》的六十四卦象之中。因此，《易经》的“象数主义”以及“乾卦”方法也成为中国古代数学思想对西方数学产生巨大影响的典型事例。

（2）传播儒家学说和著作。

客观地讲，中西文化交流过程中实质性的西学东渐和中学西渐（如对德国数学家莱布尼茨和法国启蒙思想家、作家、哲学家伏尔泰等著名学者的影响）皆始于利玛窦⁽⁵⁵⁾。利玛窦等传教士在向中国传播西方数学文化的同时，还将中国儒家学说中的大量经典著作翻译成拉丁文寄回欧洲出版发行，向西方国家介绍中国文化。

比如罗明坚翻译了《大学》的部分内容；利玛窦翻译了“四书”；卫方济编译了《中华帝国经典》；殷铎泽翻译了《论语》和《中庸》，并与柏应理一起编译了《中国哲学家孔子》；刘应翻译了《书经》和《礼记》；雷孝思（Jean Baptiste Regis，1663—1738年，字永维）编译了《中国最古之书易经》；宋君荣编译了《法文书经》等。

在自然科学方面，西方传教士突出地表现出对中药、天文历法、中国建筑的关注。

例如，邓玉函研究中国本草80余种；卜弥格（Michel Boym，1612—1659年，字致远，波兰人）的《中医津要》、冯秉正的《中国通史》论述了中医和中药；殷弘绪向欧洲介绍了中国医药和保健技巧；韩国英的《北京教士报告》论述了中国医治天花的病理和技术。

李明（Louis Daniel Lecomte，1655—1728年，字复初，被法国国王路易十四授予“国王数学家”称号）的《中国现状新记》和宋君荣的《中国天文史略》介绍了中国人对星象、日食的观察记录和干支记年法等。

在建筑学方面，兼乾隆宫廷画师的法国耶稣会传教士王志诚于1747年著《北京附近的皇室园亭》，向欧洲人详细介绍了圆明园这个中国顶级园林的特点。苏格兰建筑师威廉·钱伯斯勋爵在1757年著的《中国房屋建筑》是欧洲第一部介绍中国园林的专著。这部书影响很大，一时间中国式园林在英国和德国的大城市中如雨后春笋般出现。钱伯斯还在英国伦敦亲自设计了伦敦丘园（Kew Garden）的中国式塔。1773年钱伯斯又著《论东方园林》，德国园林艺术家路德维希·翁则尔（Ludwig Unzer）也著《中国园林论》一书。后来伦敦、波茨坦、慕尼黑、凡尔赛等地的建筑都反映了中国建筑艺术的风格。

此外，传教士还从经济、军事、地理、社会风俗方面向欧洲介绍了中国万象。除了利玛窦的《天主教传入中国史》（《利玛窦中国札记》）之外，1613年到达中国南京的葡萄牙传教士曾德昭（Alvaro Semedo，1585—1658年）于1636年返回欧洲出版了《大中国志》。

曾德昭在这部书中详细介绍了孔子和中国的教育制度，并对孔子不屈不挠的人格给予了高度的评价。他写道：

孔夫子这位伟人受到中国人的崇敬，他撰写的书以及留下的格言教导也极受重视，以至于人们不仅仅把他当作圣人，同时也把他当作先师和博士。孔夫子的话被视为神谕圣言，人们定期举行隆重的仪式以表示对他的尊崇。

曾德昭对儒家学说和思想的介绍基本真实，尤其是在社会伦理层面，对“敬天”以及如何祭祀介绍得尤为细致具体，这些内容后来在西方产生了较大的影响。曾德昭认为儒教的“敬天”思想主要在于教导人们对家族中祖先的崇拜和对朝廷的敬畏，从而演化成一种社会生活层面上的有利于统治者的伦理实践。

1736年，法国传教士杜赫德（J．B．Du Halde，1674—1743年）综合了一百多年来欧洲传教士有关中国的调查报告，编纂刊印了《中华帝国通志》。

同一时期，汉学研究和教学机构在西方大学纷纷建立。中国科技的西传启发了近代的欧洲科学家，他们开始将中国科技纳入他们的研究视野，就连英国著名生物学家达尔文（Charles Robert Darwin，1809—1882年）在研究和写作《物种起源》一书的过程中，也曾广泛涉猎传教士带到欧洲的中国科技资料。

总之，中国科技对于欧洲的影响正如李约瑟所说：“世界受惠于东亚，特别受惠于中国的整个情况已经非常清楚地显现出来。”⁽⁵⁶⁾

————————————————————

(1) 沈定平：《16—17世纪中国传教团与墨西哥教会的联系及其方法的比较研究》，《世界宗教研究》1999年第3期，第67～75页。

(2) 徐宏英：《利玛窦与〈几何原本〉的翻译》，《青岛大学师范学院学报》2008年第2期，第50～53页。

(3) ［意］利玛窦、［比］金尼阁著，何高济等译：《利玛窦中国札记　传教士利玛窦神父的远征中国史》，桂林：广西师范大学出版社2001年版，第173页。

(4) 曾峥：《利玛窦与西方数学的传播》，《韶关学院学报》2007年第6期，第1～5页。

(5) 彭必成、章太长：《试论利玛窦的灵活性传教方法》，《齐齐哈尔师范高等专科学校学报》2008年第1期，第105～106页。

(6) 关汉华：《16世纪后期天主教在广东的传播与影响》，《中南民族大学学报》（人文社会科学版）2003年第1期，第127～131页。

(7) 曾峥、刘翠平：《利玛窦在韶关对西方数学的传播及其影响（上）》，《韶关学院学报》2009年第4期，第1～5页。

(8) ［意］利玛窦、［比］金尼阁著，何高济等译：《利玛窦中国札记　传教士利玛窦神父的远征中国史》，桂林：广西师范大学出版社2001年版，第243页。

(9) 梁宗巨：《数学历史典故》，沈阳：辽宁教育出版社1995年版，第152页。

(10) 黄启臣：《澳门——16至19世纪中西文化交流的桥梁》，《比较法研究》1999年第1期，第15～36页。

(11) 沈定平：《16—17世纪中国传教团与墨西哥教会的联系及其方法的比较研究》，《世界宗教研究》1999年第3期，第67～75页。

(12) 曾峥、刘翠平：《利玛窦在韶关对西方数学的传播及其影响（下）》，《韶关学院学报》2009年第5期，第1～5页。

(13) 关汉华：《16世纪后期天主教在广东的传播与影响》，《中南民族大学学报》（人文社会科学版）2003年第1期，第127～131页。

(14) 关汉华：《16世纪后期天主教在广东的传播与影响》，《中南民族大学学报》（人文社会科学版）2003年第1期，第127～131页。

(15) ［意］利玛窦、［比］金尼阁著，何高济等译：《利玛窦中国札记　传教士利玛窦神父的远征中国史》，桂林：广西师范大学出版社2001年版，第187页。

(16) 李伯毅：《天主教第二次入华与利玛窦的贡献》，《中国天主教》2004年第4期，第39～43页。

(17) 梁宗巨：《数学历史典故》，沈阳：辽宁教育出版社1995年版，第152页。

(18) 朱大锋：《“利玛窦规矩”与明末清初的中西文化交流》，《兰台世界》2009年第7期，第38～39页。

(19) 徐宏英：《利玛窦与〈几何原本〉的翻译》，《青岛大学师范学院学报》2008年第2期，第50～53页。

(20) 郭熹微：《试论利玛窦的传教方式》，《世界宗教研究》1995年第1期，第24～36页。

(21) 田淼：《中国数学的西化历程》，济南：山东教育出版社2005年版，第25页。

(22) 彭必成、章太长：《试论利玛窦的灵活性传教方法》，《齐齐哈尔师范高等专科学校学报》2008年第1期，第105～106页。

(23) ［意］利玛窦、［比］金尼阁著，何高济等译：《利玛窦中国札记　传教士利玛窦神父的远征中国史》，桂林：广西师范大学出版社2001年版，第112页。

(24) ［意］利玛窦、［比］金尼阁著，何高济等译：《利玛窦中国札记　传教士利玛窦神父的远征中国史》，桂林：广西师范大学出版社2001年版，第120页。

(25) ［意］利玛窦、［比］金尼阁著，何高济等译：《利玛窦中国札记　传教士利玛窦神父的远征中国史》，桂林：广西师范大学出版社2001年版，第174页。

(26) ［意］利玛窦、［比］金尼阁著，何高济等译：《利玛窦中国札记　传教士利玛窦神父的远征中国史》，桂林：广西师范大学出版社2001年版，第247页。

(27) 徐宏英：《利玛窦与〈几何原本〉的翻译》，《青岛大学师范学院学报》2008年第2期，第50～53页。

(28) 李文林：《数学史教程》，北京：高等教育出版社；海德堡：施普林格出版社2000年版，第126～127页。

(29) 梁宗巨、王青建、孙宏安：《世界数学通史》（上），沈阳：辽宁教育出版社2001年版，第492页。

(30) 关汉华：《16世纪后期天主教在广东的传播与影响》，《中南民族大学学报》（人文社会科学版）2003年第1期，第127～131页。

(31) ［意］利玛窦、［比］金尼阁著，何高济等译：《利玛窦中国札记　传教士利玛窦神父的远征中国史》，桂林：广西师范大学出版社2001年版，第364页。

(32) ［意］利玛窦著，朱维铮主编：《利玛窦中文著译集》，上海：复旦大学出版社2007年版，第305页。

(33) 徐品方主编：《数学简明史》，北京：学苑出版社1992年版，第262页。

(34) 徐汇区文化局：《徐光启与〈几何原本〉》，上海：上海交通大学出版社2011年版，第147页。

(35) 汪伟、钱亦蕉等：《〈几何原本〉的大时代：星星照耀四百年》，《新民周刊》，2007年11月8日。

(36) 沈康身：《界画、〈视学〉和透视学》，自然科学史研究所、数学组编：《科学史文集（八）》，上海：上海科学技术出版社1982年版，第86～92页。

(37) 陈燮君：《利玛窦行旅中国记》，北京：北京大学出版社2010年版，第95～97页。

(38) 黄启臣：《澳门——16至19世纪中西文化交流的桥梁》，《比较法研究》1999年第1期，第15～36页。

(39) ［意］利玛窦著，朱维铮主编：《利玛窦中文著译集》，上海：复旦大学出版社2007年版，第299页。

(40) 黄启臣：《澳门——16至19世纪中西文化交流的桥梁》，《比较法研究》1999年第1期，第15～36页。

(41) 朱维铮：《走出中世纪》（增订本），上海：复旦大学出版社2007年版，第66页。

(42) 田淼：《中国数学的西化历程》，济南：山东教育出版社2005年版，第33页。

(43) 梁宗巨、王青建、孙宏安：《世界数学通史》（上），沈阳：辽宁教育出版社2001年版，第529页。

(44) 黄启臣：《澳门——16至19世纪中西文化交流的桥梁》，《比较法研究》1999年第1期，第15～36页。

(45) （清）阮元等：《畴人传汇编》，扬州：广陵书社2009年版，第536页。

(46) 闫瑞芬：《利玛窦西方数学思想的传入与意义》，《沧桑》2007年第2期，第23～24、26页。

(47) 田淼：《中国数学的西化历程》，济南：山东教育出版社2005年版，第36页。

(48) 李文潮、［德］H．波塞儿著，李文潮等译：《莱布尼茨与中国——〈中国近事〉发表三百周年国际学术讨论会论文集》，北京：科学出版社2002年版，第80页。

(49) 胡阳、李长铎：《莱布尼茨二进制与伏羲八卦图考》，上海：上海人民出版社2006年版，第61页。

(50) 胡阳、李长铎：《莱布尼茨二进制与伏羲八卦图考》，上海：上海人民出版社2006年版，第9页。

(51) 胡阳、李长铎：《莱布尼茨二进制与伏羲八卦图考》，上海：上海人民出版社2006年版，第13页。

(52) 孙小礼：《莱布尼茨与中国文化》，北京：首都师范大学出版社2006年版，第124页。

(53) 胡阳、李长铎：《莱布尼茨二进制与伏羲八卦图考》，上海：上海人民出版社2006年版，第27页。

(54) 李文潮、［德］H．波塞儿著，李文潮等译：《莱布尼茨与中国——〈中国近事〉发表三百周年国际学术讨论会论文集》，北京：科学出版社2002年版，第82页。

(55) 李伯毅：《天主教第二次入华与利玛窦的贡献》，《中国天主教》2004年第4期，第39～43页。

(56) 朱大锋：《“利玛窦规矩”与明末清初的中西文化交流》，《兰台世界》2009年第7期，第38～39页。