-
1.1前言
-
1.2第一章 奇妙的数字——提高对数字的敏感度
-
1.2.11.互不相连的数字
-
1.2.22.如何给数字分组
-
1.2.33.数字里的兵营
-
1.2.44.数字摩天轮
-
1.2.55.找规律填数字
-
1.2.66.猜点数
-
1.2.77.魔术方阵
-
1.2.88.有多少个苹果
-
1.2.99.有魔法的数字
-
1.2.1010.双胞胎的秘密
-
1.2.1111.从镜子里看数字
-
1.2.1212.字母与价格
-
1.2.1313.双环填数
-
1.2.1414.填数字
-
1.2.1515.如何划分领地
-
1.2.1616.数字金字塔
-
1.2.1717.骨牌中的数字
-
1.2.1818.房顶上的数字
-
1.2.1919.第一百个数字
-
1.2.2020.有多少个7
-
1.2.2121.想数字
-
1.2.2222.数字陷阱
-
1.2.2323.兄妹赛跑
-
1.2.2424.最大得数是几
-
1.2.2525.年龄知多少
-
1.2.2626.做作业
-
1.2.2727.报数游戏
-
1.2.2828.猜一猜是奇数还是偶数
-
1.2.2929.记不清门牌号
-
1.2.3030.门牌号的难题
-
1.2.3131.买票
-
1.2.3232.农民卖梨
-
1.2.3333.考试
-
1.2.3434.两个朋友
-
1.2.3535.巧取珍珠
-
1.2.3636.波利亚设计的趣题
-
1.2.3737.宝石窃贼
-
1.2.3838.具有特殊性质的数字
-
1.2.3939.四数之和
-
1.2.4040.相同数字
-
1.3第二章 有趣的计算——把握数字的运行规则
-
1.3.11.水上飞机问题
-
1.3.22.旅客的票价
-
1.3.33.谁的时间准确
-
1.3.44.出租车的号码
-
1.3.55.劳动者的谜题
-
1.3.66.牛奶多还是水多?
-
1.3.77.让人困惑的遗产
-
1.3.88.农夫和羊的故事
-
1.3.99.雕刻家的困惑
-
1.3.1010.苏丹的军队
-
1.3.1111.古董投资
-
1.3.1212.这些姑娘的姓名是什么
-
1.3.1313.三个孩子
-
1.3.1414.只填一次
-
1.3.1515.毛笔写字
-
1.3.1616.站成6排
-
1.3.1717.漂亮的姑娘
-
1.3.1818.一道著名的序列推算题
-
1.3.1919.卫生纸的厚度
-
1.3.2020.迷人的平方数
-
1.3.2121.桌子上的墨迹
-
1.3.2222.谦虚有礼的学生
-
1.3.2323. 33颗珍珠
-
1.3.2424.干草堆
-
1.3.2525.油漆灯柱
-
1.3.2626.雾中的歌本思先生
-
1.3.2727.抓贼
-
1.3.2828.改变了的守财奴
-
1.3.2929.一个栅栏的问题
-
1.3.3030.环绕的方格
-
1.3.3131.汤姆的年龄
-
1.3.3232.自动扶梯的阶数
-
1.3.3333.宠物兔子
-
1.3.3434.彩票竞标
-
1.3.3535.提前回家
-
1.3.3636.给爸爸出题
-
1.3.3737.机智的客人
-
1.3.3838.宝石分配问题
-
1.3.3939.国际会议
-
1.3.4040.新版龟兔赛跑
-
1.3.4141.“远洋”号邮轮
-
1.3.4242.猎豹与老虎
-
1.3.4343.奇怪的数学题
-
1.3.4444.商家的让利
-
1.4第三章 变幻莫测的几何——培养形象思考的能力
-
1.4.11.涂黑的三角形
-
1.4.22.有意思的五角星
-
1.4.33.花瓣图形问题
-
1.4.44.多出来的十字架
-
1.4.55.巧绘曲线
-
1.4.66.一个木匠的难题
-
1.4.77.壁炉前的地毯
-
1.4.88.添棋子
-
1.4.99.两块马蹄铁
-
1.4.1010.背道而行的小鱼
-
1.4.1111.圣乔治的旗帜
-
1.4.1212.改变朝向
-
1.4.1313.鱼头向右
-
1.4.1414.太阳与风车
-
1.4.1515.三角形变六边形
-
1.4.1616.火柴正方形
-
1.4.1717.一弓变二口
-
1.4.1818.扩大总面积
-
1.4.1919.巧变三角形
-
1.4.2020.圆盘中的棋子
-
1.4.2121.扑克牌金字塔
-
1.4.2222.堆火柴
-
1.4.2323.手表上的谜题
-
1.4.2424.平衡天平
-
1.4.2525.寻找缺失的图
-
1.4.2626.拼凑正方形
-
1.4.2727.贪婪的巴河姆
-
1.4.2828.酒杯与瓶口
-
1.4.2929. 4颗人造卫星
-
1.4.3030.变废为宝
-
1.4.3131.精练的数学语言
-
1.4.3232.走过的路线
-
1.4.3333.钱币的重量
-
1.4.3434.黑点的运动轨迹
-
1.4.3535.分等积图形
-
1.4.3636.拼正方形
-
1.4.3737.分圆
-
1.5第四章 方程中的秘密——训练数学运算的能力
-
1.5.11.趣凑等式
-
1.5.22.算术积木
-
1.5.33.巧妙添加减号
-
1.5.44.连环等式
-
1.5.55.会跳舞的小方格
-
1.5.66.“爱”的谜题
-
1.5.77.生肖等式
-
1.5.88.狼和羊的故事
-
1.5.99.茶楼里的问题
-
1.5.1010.奇数的圈套
-
1.5.1111.币值不同的硬币
-
1.5.1212.找次品
-
1.5.1313.聪明的小孙子
-
1.5.1414.精心的米奇小姐
-
1.5.1515.殊途同归
-
1.5.1616. 8个奇数组合
-
1.5.1717.及格的人数
-
1.5.1818.巧算年龄
-
1.5.1919.找规律
-
1.5.2020.禅师的念珠
-
1.5.2121.一个大数
-
1.5.2222.书的页数
-
1.5.2323.母子的年龄
-
1.5.2424.巧算平方的秘诀
-
1.5.2525. 3只家禽
-
1.5.2626.环形公路上的骑行
-
1.5.2727.陆地的面积
-
1.5.2828.追小偷
-
1.5.2929.采购文具的成本
-
1.5.3030.打折商品
-
1.5.3131.发车间隔
-
1.5.3232.步行的路程
-
1.5.3333.七个小矮人
-
1.5.3434.哲学家的弟子
-
1.5.3535.冷饮店的利润
-
1.5.3636.汽车的速度
-
1.5.3737.瞎子看瓜
-
1.5.3838.关公卖刀
-
1.5.3939.检票窗口
-
1.5.4040.两只股票
-
1.5.4141.蜡烛谜题
-
1.6第五章 概率的问题——练就宏观思考的本领
-
1.6.11.打开房门的钥匙
-
1.6.22.王子求婚记
-
1.6.33.代表选举
-
1.6.44.幸运观众
-
1.6.55.两数之差
-
1.6.66.交换明信片
-
1.6.77.选择公交车
-
1.6.88.交通肇事事件
-
1.6.99.换还是不换
-
1.6.1010.老兵的训话
-
1.6.1111.谁活下来的概率大
-
1.6.1212.你能猜出这张牌是什么吗
-
1.6.1313.小牛为何能赢了象棋高手
-
1.6.1414.赢得比赛
-
1.6.1515.每隔一个背一个
-
1.6.1616.抛硬币
-
1.6.1717.吃糖的学问
-
1.6.1818.辨别铅球
-
1.6.1919. 3个囚犯
-
1.6.2020.必赢的下注法
-
1.6.2121.控制开关
-
1.6.2222.录取概率
-
1.6.2323.晚会上的抽奖
-
1.6.2424.被录取的人
-
1.6.2525.随堂测验及格率
-
1.6.2626.老师的胜算
-
1.6.2727.什锦粽子
-
1.6.2828.摸彩球
-
1.6.2929.掷硬币问题
-
1.6.3030.联谊活动
-
1.7第六章 排列组合的方法——训练分类归纳的能力
-
1.7.11. 15只绵羊
-
1.7.22.亚瑟王的骑士
-
1.7.33.城市午餐
-
1.7.44.旅行与发现
-
1.7.55.错误的帽子
-
1.7.66.船里的3个人
-
1.7.77. 15个字母谜题
-
1.7.88.三块手表的时间
-
1.7.99.一个集体宿舍之谜
-
1.7.1010.捕鼠器谜题
-
1.7.1111.筹码十字架
-
1.7.1212.油漆一个棱锥
-
1.7.1313.古董商人的锁链
-
1.7.1414. 4枚邮票
-
1.7.1515.建四面体
-
1.7.1616.编钟的谜题
-
1.7.1717. 9个男生
-
1.7.1818.圆桌
-
1.7.1919.拿粉笔
-
1.7.2020. 13片花瓣
-
1.7.2121.月历的排列问题
-
1.7.2222.哪两位是姐妹
-
1.7.2323.买邮票
-
1.7.2424.老师的生日
-
1.7.2525.运动的蚂蚁
-
1.7.2626.田间问题
-
1.7.2727.选择工人
-
1.7.2828.数字卡片
-
1.7.2929.买手套
-
1.7.3030.排头与排尾
-
1.7.3131.质量测试
-
1.7.3232.关路灯的方法
-
1.7.3333.传球练习
-
1.7.3434.不含4的数字
-
1.7.3535.台阶上的兄弟
-
1.8第七章 路径选择问题——发现数学问题中的最优解
-
1.8.11.一个青少年的谜题
-
1.8.22.英国国旗的问题
-
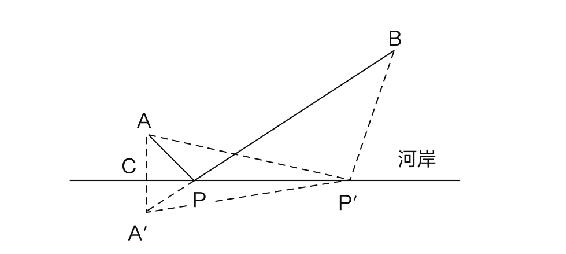
1.8.33.穿过小溪
-
1.8.44.如何穿过房间?
-
1.8.55. 15个转弯
-
1.8.66.多种解法
-
1.8.77.小猫吃鱼
-
1.8.88.五个嫉妒的丈夫
-
1.8.99.投票者的难题
-
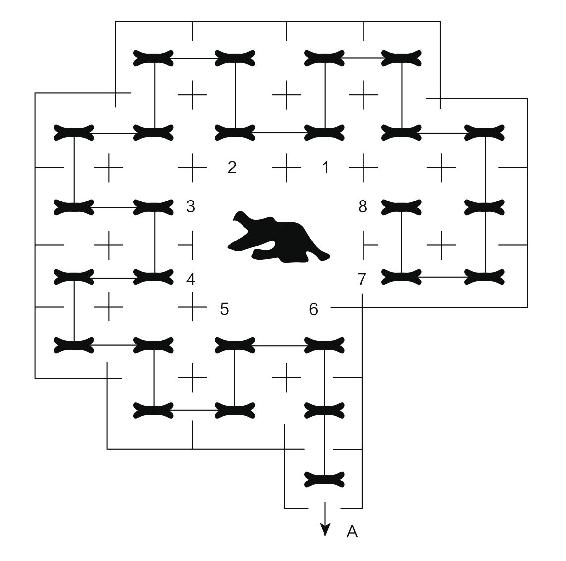
1.8.1010.小狗啃骨头
-
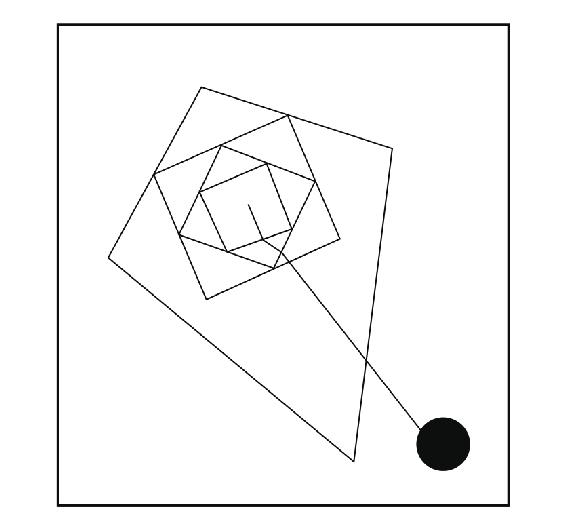
1.8.1111.一笔画出一个风筝
-
1.8.1212.打结的绳子
-
1.8.1313.地铁巡视员的谜题
-
1.8.1414.两车相距多少千米?
-
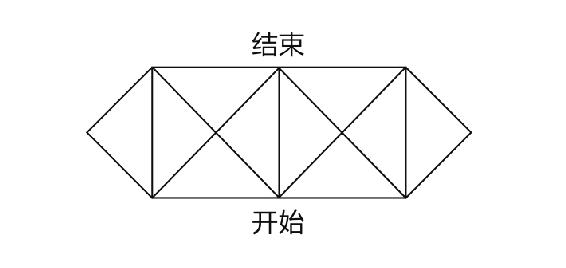
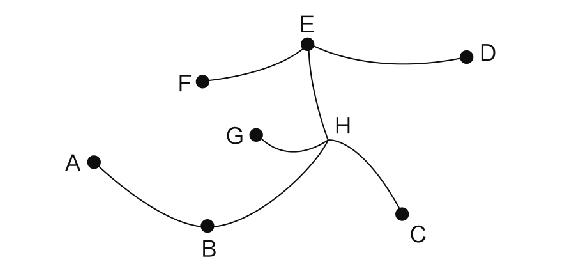
1.8.1515.一笔连线
-
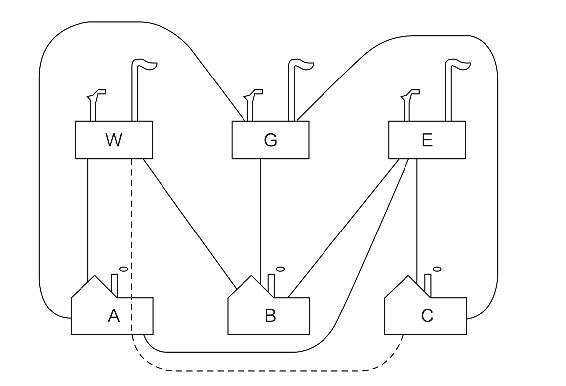
1.8.1616.水、燃气和电
-
1.8.1717.公共休假日的谜题
-
1.8.1818.丙车的速度是多少?
-
1.8.1919.错乱的数字
-
1.8.2020.汉娜的谜题
-
1.8.2121.骑士和他忠诚的狗
-
1.8.2222.铁路谜题
-
1.8.2323.旅行者过桥
-
1.8.2424.小镇邮递员
-
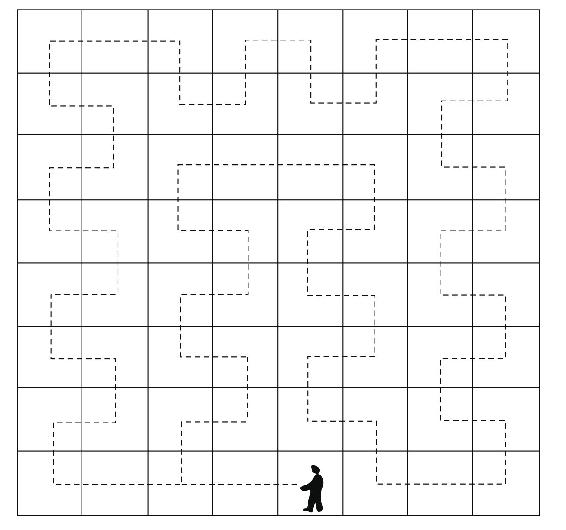
1.8.2525.环绕海岸
-
1.8.2626.骑士的路线
-
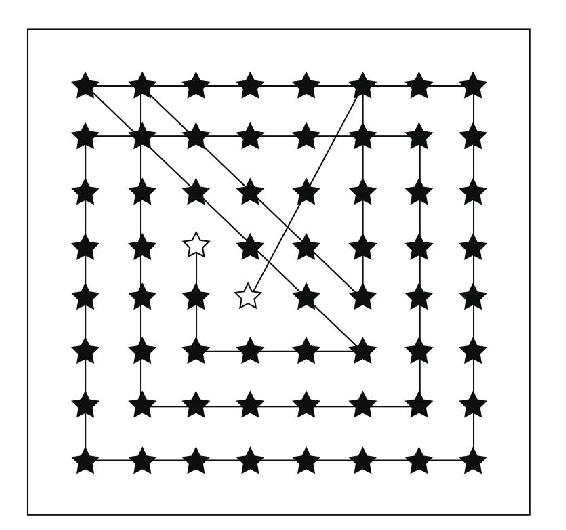
1.8.2727.星星谜题
-
1.8.2828.交换位置的谜题
-
1.8.2929. 12枚硬币
-
1.8.3030.地牢里的谜题
-
1.8.3131.字母块谜题
-
1.8.3232.租房子的难题
-
1.8.3333.架设电线
-
1.8.3434.汽车车库问题
-
1.8.3535.五边形街道
-
1.9第八章 精密的应用题——养成周密的思考习惯
-
1.9.11.柏拉图学院中的难题
-
1.9.22.农妇卖鸡蛋
-
1.9.33.准确的案发时间
-
1.9.44.轮船相遇
-
1.9.55.奇怪的数列
-
1.9.66.妙法取盐
-
1.9.77.房地产开发
-
1.9.88. 5层金字塔
-
1.9.99.肥肉和瘦肉
-
1.9.1010.准确时间
-
1.9.1111.地球和篮球
-
1.9.1212.老师猜数
-
1.9.1313.狗跑的距离
-
1.9.1414.发新书
-
1.9.1515.钟没有停
-
1.9.1616.师傅和徒弟
-
1.9.1717.海盗分金子
-
1.9.1818.大象和蚊虫
-
1.9.1919.椰子的数量
-
1.9.2020.兄弟搬砖
-
1.9.2121.粗心的饲养员
-
1.9.2222.刁藩都的年岁
-
1.9.2323.李白买酒
-
1.9.2424.危险的隧道
-
1.9.2525.打野猪
-
1.9.2626.卖帽子
-
1.9.2727.数学诗
-
1.9.2828.猎人与子弹
-
1.9.2929.数学博士的法眼
-
1.9.3030.算年龄
-
1.9.3131.旅行花销
-
1.9.3232.换空瓶的学问
-
1.9.3333. 3个人吃包子
-
1.9.3434.公交车站上的数学
-
1.9.3535.现在是几点了
-
1.9.3636.渔夫和草帽
-
1.9.3737.巧算比分
-
1.9.3838.座位循环
1
最强大脑训练课:提升逻辑力的300个数学游戏