第四章
儿童言语表达与“言语的起源”
我们在前文论述词语—用途时发现了n的重要性，即特定个人词汇中不同词语数量多少的重要性。现在我们将从实证和理论上研究n数值变化这个问题。既然儿童词汇量变化十分广泛早就众所周知，我们将在本章集中精力专门研究儿童的言语表达。我们这种专心研究会更加容易，因为儿童言语这个主题对于那些在儿童发展研究这个普通领域中经验丰富的众多研究人员而言格外重要，以至于我们可以在他们的研究成果中找到我们全部数据分析所必需的原材料1。
我们现在研究儿童词汇的多少，不是从整个儿童发展领域的背景来处理这个问题。相反，我们是从研究成人英语言语的案例中全新对待这个问题，其中最重要的是，我们发现了双曲线方程式r×f=C及其推论的调和级数方程式F·Sn[1]。此外，在我们接下来探讨儿童言语的过程中，我们会偶尔关注整个儿童发展领域中非语言的背景，因为从我们主要兴趣来看建议研究儿童语言表达方式只是因为它们恰巧给我们提供了一个极佳机会去研究最省力原则的某些内容，显然这在其他研究中无法这般容易即可获得。
第一节 问题
在转到儿童这个问题时，我们不仅要回顾第二章开篇讨论统一化与多样化两个基本力量时说过的话，而且还要记得我们没有说过的话。因为虽然我们详细地论述了某特定说话人词汇量大小导致的相冲突的经济优势，但是我们从未限定该说话人必须是成人而不可以是儿童。相反，我们却知道，有关统一化之力与多元化之力的全部论述可以自动且完全适用于儿童言语表达，由此我们现在就转而从定量角度探讨这一问题。
儿童比成人词汇少，单纯这个事实本身不能解释不存在双曲线方程r×f=C或者调和级数方程式：
F·Sn=F/1+F/2+F/3+…+F/n
因为在减少n的数值时，我们只是减少（1）Sn的数值、（2）等同于n的C的数值以及（3）F的数值，我们认为F是等于n（即，F/n=1）。反之亦然，我们增加n的数值时也会相应地发生变化。
不过总的来看，在这一点上我们或许应该记住：随着n在算术上增减，Sn相应地只在对数上增减，结果导致词汇量大小n（以及F·Sn的数值）的差异对于观察者而言更加格外明显而不是更加隐晦，但是Sn的差异同样特别重要。的确，由于n和Sn之间的关系不仅对于本章而且对于整本书来说都是最重要的，或许我们很有必要暂时离开这个主题，为了解释的需要，我们在接下来的表4-1中呈现了不同词语的大概数量n，以及大概最优规模（optimum size）的样本F·Sn（其中F=n），而最优样本对于一些任意挑选的Sn值要满足调和级数方程式是必需的。
表4-1
即便扫一眼表4-1中三个立柱，也足以表明存在一个巨大变化，这个巨变也许既来自词汇中不同词语数量又来自相对变化较小的Sn数值的最优规模样本。为了实际分析的目的，这可能相当令人费解，因为我们除了根据最优规模样本无法计算出斜率，可是我们只有在知道最优样本的Sn数值之后才可了解样本的最优规模是多少，而且我们只有根据最优规模样本才能计算出Sn值。因此我们陷入一个进退两难的小困境。
不过，只要我们有耐心总会有出路的。因此，对于某特定儿童我们可以选择一些连续词语数量不同的样本，这些不同样本的规模Σ在篇幅长短上变化很大。我们将每个样本的词语减少至序列—频率分布，且分别绘制成图，然后找到一个最接近-1斜率的样本，因为最接近-1斜率的样本同时也会最接近我们可以放心运算的最优规模的条件。
一旦我们找到了一个差不多是最优规模的样本，我们就能计算出该样本最佳直线的实际斜率，该斜率应该近似于-1。基于此信息，我们还可以计算出这条最佳直线的Y-截距；这个Y-截距就是频率最高词语的理论频率F（即，该词语r=1）。接着根据这个假设即样本规模Σ近似于F·Sn，我们可以用我们计算出的理论值F除Σ，由是洞悉出儿童言语的Sn数值，因而让我们自身摆脱出我们的窘境。
在推导出一个儿童语言表达的Sn信息之后，我们可以扩展分析不同年龄的一群儿童的言语表达，以便研究儿童言语表达大体上在多大范围内适合用方程式r×f=C以及F·Sn来描述。
第二节 定量数据
我们现在转而定量研究儿童言语词语的序列—频率分布，我们将分两部分来研究。在第一部分中（1）我们将研究一个儿童在5到7岁时不同时期言语样本的词语分布［在下文，是《乌尔布罗克语料》（Uhrbrock Material）］。在第二部分中（2）我们将研究一群儿童在包括22个月到59个月之间不同年龄时期各自言语流样本中词语分布［在下文，是《费希尔语料》（Fisher Material）］。
一、乌尔布罗克语料
图4-1呈现了一些连贯言语样本的不同序列词语（在X轴上）及其各自频率（在Y轴上）的9组序列—频率分布，这些言语是一个小女孩在其差不多第5个、第6个、第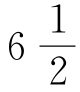
个以及第7个生日时口述，由乌尔布罗克（R.S.Uhrbrock）用留声机记录的，承蒙他将这些语料交由我处理，这些语料包括：他记录的词语频率手稿和他对5岁时样本所作的统计数据列表，以及这位女孩在将近6岁、6岁半和7岁时口述的记录手稿2。
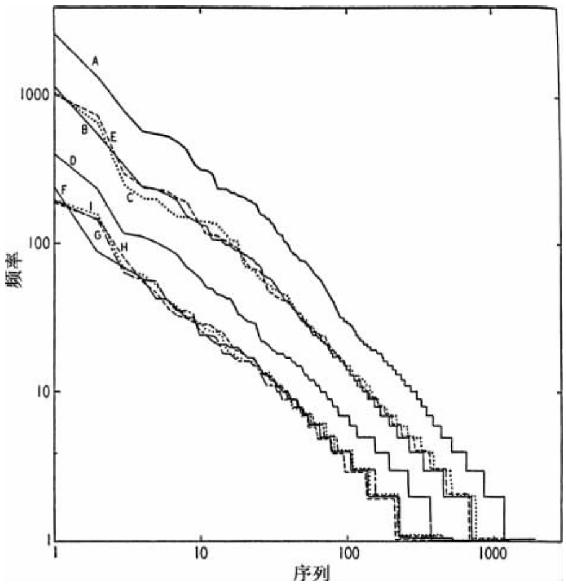
图4-1 （乌尔布罗克语料）小女孩不同年龄时词语的序列—频率分布：（A）5岁时24 000个词语；（B）5岁时10 000词语；（C）6岁半时10 000个词语，（D）6岁时4 000个词语；（E）7岁时10 000个词语；（F）、（G）、（H）和（I）每个上述年龄2 000个词语（数字是指样本的长度）。
在图4-1中，曲线A代表5岁时语料总计约为24 000个连续词语；曲线B代表同一语料中前10 000个连续词语；曲线C代表6岁半时语料的10 000个连续词语；曲线D代表6岁半到7岁时语料的4 000个连续词语；曲线E代表7岁时语料的10 000个连续词语；而曲线F、G、H和I分别是指5岁、6岁、6岁半和7岁时语料的前2 000个连续词语。
我们在审视图4-1中9条曲线时发现，它们从左向右下降的方式既是总体上相似的，又是总体上相当接近-1斜率（例如，它们更接近-1而不是-2或者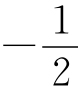
。诚然，它们在直线上呈现的弯曲比图2-1中《尤利西斯》和埃尔德里奇曲线的情况更加显著；此外，不同曲线的有些弯曲看起来是有系统的，也就是说它们在位置、方向和量值上差不多彼此对应，非常像是这位女孩已经形成了某种固定的言语风格。而且，随着我们审视9条曲线的总体斜率，不经意中仿佛更大样本的总体斜率要比更小样本的稍微陡峭些，这一点正是我们可能预料到的，如果更大样本超过最优规模目标就会如此，而最优规模显然应当在最短样本中找到3。既然我们主要兴趣在于最优规模样本，那么我们现在可以集中注意力关注有2 000个连续词语的样本，这样做十分有利。
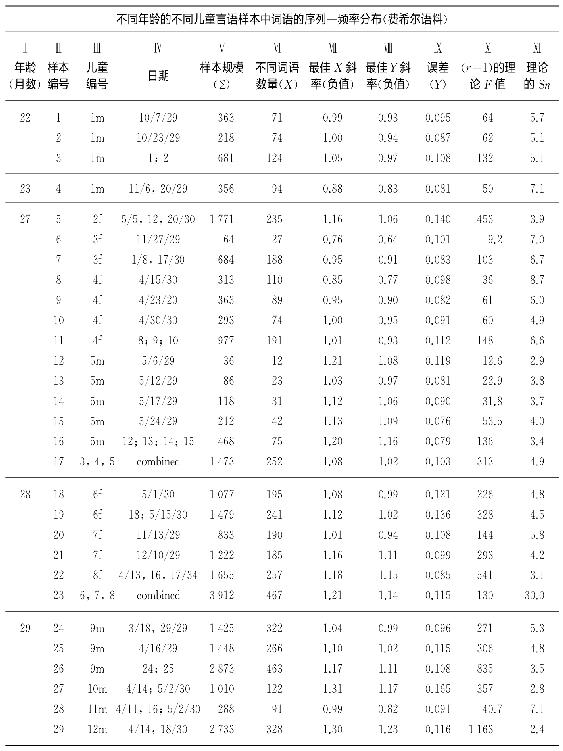
我们来把5岁、6岁半和7岁时三个10 000词语的样本以及6岁时4 000词语的样本各自分解为成分连贯的2 000个词语的样本，那么我们将得到5岁、6岁半和7岁时语料各自有五个2 000个词语的不同样本，以及6岁半到7岁时语料有两个2 000个词语的样本。我们在表4-2中呈现了更加精细定量分析的详细结果。在表4-2栏Ⅰ中是说话人的年龄；栏Ⅱ中是样本数量；栏Ⅲ中是样本连续词语的规模Σ；栏Ⅳ中是不同词语或序列的数量X；栏Ⅴ中是根据X由最小二乘法计算出的最佳斜率（负值）；栏Ⅵ中是根据Y由最小二乘法计算出的最佳斜率（负值）；栏Ⅶ中是偏离栏Ⅵ中Y的最佳直线的均方根误差；栏Ⅷ中是Y最佳直线的Y-截距的逆对数（这与词语r=1的理论频率F是相同的）；栏Ⅸ中是理论上的Sn，Sn值是栏Ⅲ中数目（即Σ=样本长度）除以栏Ⅷ中对应的数目（即理论频率F）的结果。
表4-2
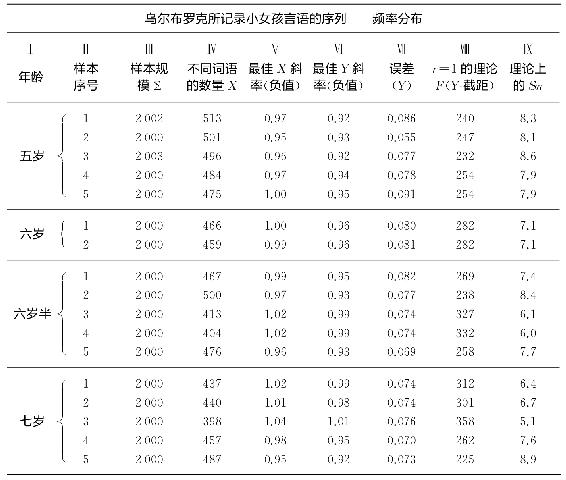
我们在审视栏Ⅴ或者Ⅵ的（我们知道两者中选谁没有理论原因）的最佳直线的负斜率时发现，计算出的负斜率与理论上的负斜率1极其近似。而且，从栏Ⅶ中相对较小的误差中我们可以认为，我们计算出的最佳Y线相当接近实际的点。因此，根据我们第二章的论述，我们毫不迟疑地认为，双曲线方程式r×f=C及其姊妹调和级数方程式F·Sn总体上十分精确地描述了这位女孩在5岁、6岁、6岁半以及7岁时的不同言语表达。
如果我们审视栏Ⅸ中理论上的Sn的不同数值，我们会发现它们在8.9和5.1这两极之间变化，平均值为7.6。虽然我们稍后将再次详细论述理论值Sn的变数，但是，我们甚至现在也可以大致浏览一下表4-1，我们从中发现，在Sn等于7时我们有望发现在大约4 300个连续词语的样本中有大约600个不同词语。这一点很有意思，因为栏Ⅳ中不同词语的实际数量X以及栏Ⅲ中我们样本的实际长度Σ两者都是Sn约为7时应该得出的一般数量。诚然，栏Ⅳ样本中那些词语都是比Sn=7时理论上预计的600个词语要少。可是这种差异在我们看一眼图4-1中曲线的弯曲部分就会释然，图中曲线的中间部分向上凸面揭示了中间值频率的词语往往使用得过于频繁。显然，中间频率的一些词语使用过于频繁，任何这类倾向都会通过如下方式得到补偿：要么减少F数量或n数量，要么两者数量都减少，我们17个样本的情况明显就是如此。
不论所有这些因素，显著的事实依然是（栏Ⅴ和栏Ⅵ）计算出的最佳斜率几乎就是我们理论上所预期的[2]。因此我们到目前为止已经精彩地在实证上准确证实了双曲线方程式r×f=C及其含义。
二、费希尔语料
既然我们已经检测了一个女孩在5到7岁不同时刻言语记录的序列—频率分布，结果肯定了我们双曲线方程式以及含义，我们现在的任务就是检测其他儿童言语的序列—频率分布，以便判定我们在多大程度上可以根据乌尔布罗克的发现加以推广。
幸运的是，玛丽·沙托克·费希尔（Mary Shattuck Fisher）博士在哥伦比亚大学师范学院的儿童发展研究所存档了她记录的儿童言语，她据此写出了有关学龄前儿童言语的优秀专著4。洛伊丝·海登·米克（Lois Hayden Meek）博士，该研究所的所长，大方热情地许可我的研究助手对于费希尔博士的记录（费希尔语料）制作了副本。
费希尔语料，如同费希尔博士专著中所描述的，是由幼儿园儿童言语的书面记录构成。这些样本必然长短不一，有些儿童的言语表达在日后又作了记录。为了阐释和比较的目的，有些情况下我们不仅分析了（1）某特定儿童在某特定日期整个言语样本的频率分布，而且分析了（2）不同规模样本的构成部分以及偶尔分析了（3）几个同龄孩子的联合样本。
我们统计分析的结果即刻呈现于表4-3中。其中，栏Ⅰ代表了用足月数量计算的年龄（因此，例如，22个月包括从22个月的每一天直至第23个月开始的那一天）。栏Ⅱ中呈现了整个表格中每个连续样本的编号。栏Ⅲ呈现了每个儿童的身份编号（以便隐藏其真实身份）另加上字母m或f以注明这位儿童是男性还是女性；通过这些编号我们也能识别某特定儿童日后的再次言语采样。栏Ⅳ中呈现了费希尔博士做记录的日期。栏Ⅴ中呈现了样本的规模Σ，即该样本包含的连续词语数量。栏Ⅵ中是样本里不同词语（序列）的数量。栏Ⅶ和栏Ⅷ中分别为最佳X线和最佳Y线的（最小二乘法）负斜率；栏Ⅸ中是最佳Y线的误差（均方根差）。栏Ⅹ中是最高频率词语的理论频率F（最佳Y线的Y-截距的逆对数；栏Ⅺ中是理论上的Sn值（栏Ⅴ中数目Σ除以栏Ⅹ中相应数目之后的值）。
表4-3
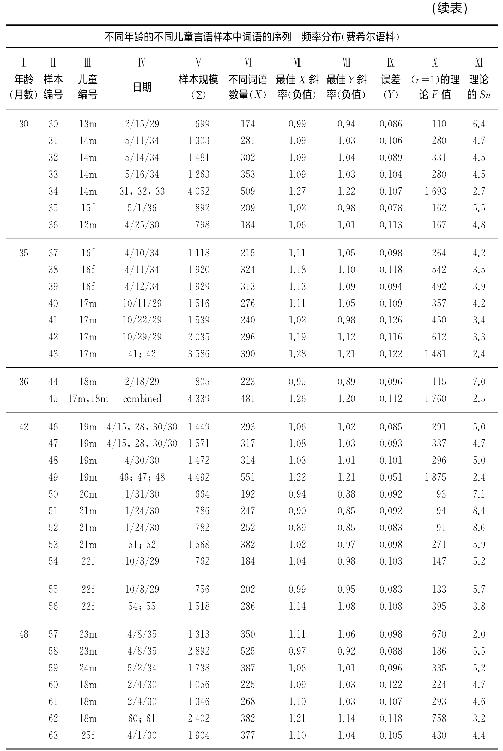
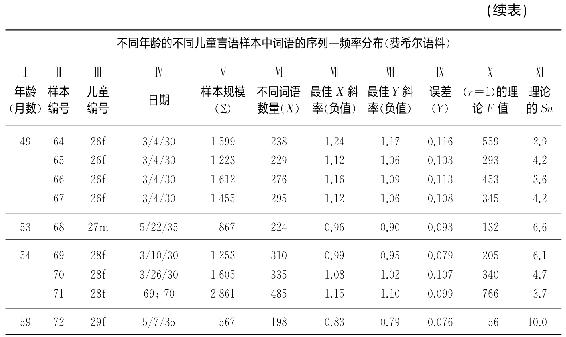
一旦同一个儿童的不同样本呈现了相同日期（如，编号为64，65，66，67的样本），这就表明，这位儿童在当天记录的长篇言语已经被分解成较小的连续部分，各部分的长度可能是或不是相等的；我们进行这种分拆不仅是希望更加接近最优规模，而且欲求研究样本规模Σ的差异可能伴随的斜率差异。我们抱着相同的希望和欲求汇聚了同一位儿童在差不多同一时间的不同样本；如此汇聚实例可见于栏Ⅳ中日期下插入的不同联合样本的样本编号（参见如下编号的样本：3，11，16，26，43，49，53，56，62，71）。因此，如果读者在栏Ⅳ中发现的是编号而不是日期，他会明白他面对的是这些编号所指的样本组合。
最后在三种情况下（样本编号为17，23和45），是不同儿童样本的组合，而该儿童的身份编号可见于栏Ⅲ中，这些不同儿童的言语组合，当初放置在此是为了说明组合不同样本的危险，即便现在也可忽略掉，因为它们是统计的人造物。
读者在审视表4-3中数据时会发现，存在着相对而言的小误差，其中特定言语的样本组合与其成分总和并非完全一致（如，第34号样本有4 052个连续词语，而不是4 047个）。据我们所了解，这些误差既非频繁又非重要。鉴于所涉及的统计任务的范围，我们恳请读者谅解这些计算误差以及整部书中可能发现的任何其他误差。
我们在审视表4-3中数据时，集中注意力关注栏Ⅶ和栏Ⅷ中负斜率，发现它们惊人地近似于理论预期的负斜率1。七十二条最佳Y斜率的平均值是1.02。此外，如果我们忽略这些72个不同斜率中小数点后面第二位数字，我们会发现该模式即为负1.0（用斜体字表示的负斜率是如此分布的：0.6，1；0.7，2；0.8，6；0.9，19；1.0，27；1.1，12；1.2，5）。
考虑到表4-3所揭露的本质，我们毫不犹豫地说，费希尔博士的语料如同乌尔布罗克语料一样揭示出儿童言语非常接近双曲线方程式及其推论出的调和级数方程式。
当然，斜率有差异，正如我们在样本规模差异中应当预见的，如果我们记得第二章论述饱和现象以及样本最优规模，情况也如此。总体而言，（栏Ⅶ和栏Ⅷ）斜率大小往往随着样本大小（栏Ⅴ）的增加而增加，尽管我们发现误差（栏Ⅸ）很少随着样本规模（栏Ⅴ）发生变化或者也不会随着不同序列与样本规模的比例（栏Ⅵ中数目除以栏Ⅴ中相应数目）发生变化。
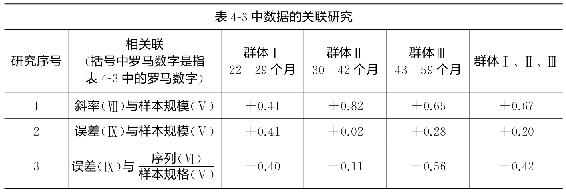
为了对于斜率、样本规模、误差以及序列—样本—规模之间的关系给出稍微更加精确的概念，我们将表4-3中数据分成如下三组年龄群体：Ⅰ，22—29个月；Ⅱ，30—42个月；以及Ⅲ，43—59个月。接着在表4-4中我们呈现出对于它们之间可能存在的关系的研究结果：（1）斜率（表4-3中栏Ⅷ的）与样本规模（同表中栏Ⅴ的）之间可能存在的关系；（2）误差（同表中栏Ⅸ的）与样本规模（同表中栏Ⅴ的）之间可能存在的关系；以及（3）误差（同表中栏Ⅸ的）与（同表中栏Ⅵ的）各个序列除以样本规模（同表中栏Ⅴ的）的商之间可能存在的关系。
审视表4-4揭示了（1）总体上斜率与样本规模成正比例关系；即，样本越大，它的斜率可能越陡峭（正如我们在论述不完全饱和现象、饱和现象以及过饱和现象时多少已经预料到的）。另一方面，误差（2.3）意义不大。
表4-4
虽然表4-4去掉了表4-3中斜率和误差的次要点数，但仍然保留了表4-3栏Ⅺ中的数目（理论上的Sn值），这些数目值得我们粗略考量一下。这些数目如同乌尔布罗克语料中相应数目，变化非常大。然而除了第23号和72号样本之外，Sn明显不到10甚至不到9，只有三个样本大于8。第23号样本中Sn=30，特别显眼，倘若它不是误算出的话（大概不会），它揭示了将不同人的言语样本组合一起存在着风险（但是请注意，组合样本17和45明显相近）。第72号样本中Sn突然又是10.0，这很可能只不过是个“意外”[3]。可是除此之外，表4-3中费希尔语料的Sn上限值与表4-2中乌尔布罗克语料的上限值是相近的，虽然费希尔语料的Sn下限值要远远低于乌尔布罗克语料的下限值——大概这是由于费希尔语料的群体年龄小些的缘故。
至于其他可能的关联，比如斜率与该儿童性别之间的差异，我们将这些关联留给那些对此感兴趣的人去研究，因为我们的主要兴趣还是在于阐释最省力原则，我们认为是最省力原则的运作导致了本章数据的本质以及条理性。
费希尔语料强有力地证实了我们的实证研究所得，它表明了即使是婴儿语言也会如此接近-1斜率。有些误差的大小显示，儿童有时候在使用成人“词语工具”时有些稚嫩，但还是非常接近双曲线程式5。
三、儿童模仿言语（Echolalia）（仍然是费希尔语料）
回想起来，我们必须承认费希尔语料给我们带来了一些为数不多的分类困难。我们这么说主要是指将记录的某些儿童话语按照正式词语范畴进行分类存在着困难。
这些分类困难有两种。第一种也是不那么严重的困难在于给诸如“brabrabrabra”言语分类，顺便说一句，该言语在第3号样本中碰巧重复了两次（该样本中还有26个其他类似的非文化言语，加上前一个，该样本680个连续词语中总计出现了42次此类表达）。
第二个也是更加严重的困难在于如何处理直接重复的正式词语（即，模仿言语）。因此，例如，第3号样本中，有个最高频率的词语“grandma”，总共出现了97次，其中有85次是12组不同直接重复词语绑定在一起的，这12簇词语就并列的grandma而言各自规模分别为：33，14，10，8，4，3，3，3，2，2，2，2（这个调和比例的近似值可能是偶然的）。第二个最高频率词语是“duck”，出现了51次，分别有27、7和3的三簇并列表达。第三个最高频率词语是“daddy”，总共出现了30次，包括9、9、3和2的四簇并列表达。第四个最高频率词语是一个专有名词，出现了27次，其言语簇是6、5、2、2、2、2、2和2。列表中其他词语以此类推。的确，为了说教的意义我们在此呈现22个月大（尚未满两岁！）的小孩在1929年10月7日记录的第1m号样本的开篇言语（模仿言语通常被界定为自动的且“无意图的”重复词语）。
Grandma. Grandma. Buggy. Baby. Baby crying. Baby crying. Baby crying.
Grandma. Grandma here. My ball. Baby girl. Munner. All through.
Yes. Grandma. Grandma. Grandma. Grandma. Grandma. Grandma.
Grandma. Grandma. Stand up. Stand up. Grandma. Grandma. Grandma.
Grandma. Grandma. Grandma. Grandma. Grandma. Grandma. Grandma.
“Bill's” hat. Coat. Coat. Put my sweater on. Put my sweater on. Grandma.
Sit down. Grandma sit down. Grandma. Grandma. Grandma. Grandma.
Grandma. Grandma. Grandma. Grandma. Grandma. Grandma. Grandma.
Grandma. Grandma. Grandma. I got blocks. I got blocks. Hat. My ball.
Look. Look. Look. Ball. Ball. “Mary.” Ball. Ball. Ball. Ball. Grandma.
Grandma. Grandma. Grandma. Hat. Hat on. Mmmmmmmm. Paper.
Paper. Paper. Paper. Munner-mandeet，mandeet, mandeet，mandeet，
mandeet, mandeet-seebeesh, seebeesh, seebeesh, seebeesh, seebeesh, bub-abubububububububub.ooooooo oo oooo.
Grandma（总共重复了33次），Grandmah（总共重复了11次）。
样本1和样本2也是依此类推（这两个样本结合在一起导出了样本3）。
这种“文理不通的话”的成分应该如何分类？我们不知道。我们只知道我们把所有这些类“词语”都计算在内，包括类“词语”的重复以及所有像类“词语”的“非文化言语”。于是我们发现这种“文理不通的话”，比如像样本1、2和3所记述的，其最佳X斜率（负值）分别为0.99和1.00和1.05（Y斜率分别为0.93、0.94和0.97）。因此，我们可以说这位男孩所记录的言语不仅与整个样本中他的“文理不通的话”相一致，而且还揭示了他的幼年言语“作坊”中存在着一种词语用途的双曲线经济，这与詹姆斯·乔伊斯在乔伊斯成人言语“作坊”中的双曲线经济相类似。
或许我们应该知晓我们是否应该从我们的列表中排除所有这些非言语实体以及所有这些模仿言语的实例，因为它们并非“词语”。我们只能说，不管我们谈论“词语”时仔细研究了许多词语，我们还得去探明什么是词语，虽然有关这一主题我们将在下一章作更多论述。据我们所了解，在上述样本中seebeesh和bubabubu等言语听起来像是狗的“汪汪”叫，它们对于婴幼儿的言语表达担当的关系与成人正式词语对于成人言语表达担当的关系是一样的。因此，诸如seebeesh一类言语也许只是未成年人非文化言语，我们决不能考虑把它们排除在外（此类“未成年人非文化言语”在30个月大之后就没有统计意义了；甚至在样本3中它们在全部样本680个连续词语中只有42个）。
表4-5
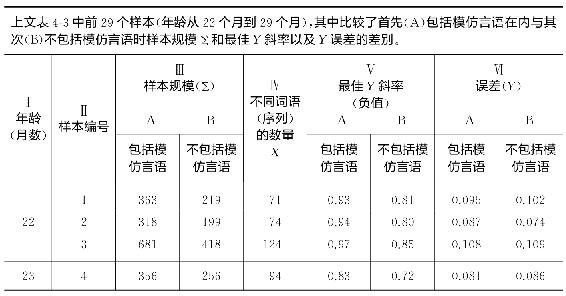
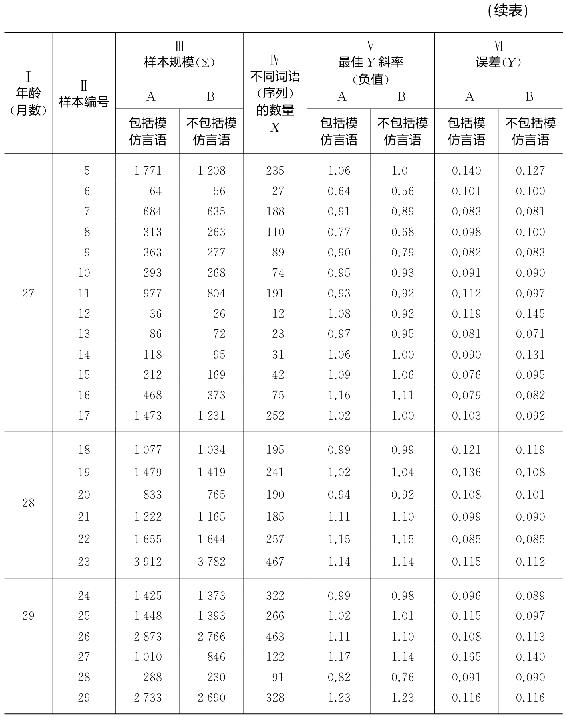
但是，即便我们在样本中保留了“未成年人非文化言语”，我们或许应当排除模仿言语吗？排除模仿言语很容易，只要将它从样本中删除即可，再用误差重新计算最佳Y斜率。在此情况下，表4-3栏Ⅵ中不同词语（序列）数量依然相同，虽然（表4-3）栏Ⅴ中样本规模Σ将会缩减到去除重复词语的数量（在样本1中去除模仿言语使该样本的连续词语由363个减少至219个）。
为了说明表4-3前29个样本（年龄群从22个月到29个月，此后模仿言语已没有统计意义）删除模仿言语后的影响，我们在表4-5中呈现了上述几个样本排除所有模仿言语之后用最小二乘法计算最佳Y斜率（负值）和Y误差（均方根差）的值。表4-5栏Ⅰ中我们看到的是年龄群，栏Ⅱ中是来自表4-3的样本编号。栏ⅢA是包括模仿言语的样本规模（与表4-3栏Ⅴ中数值相同），而栏ⅢB是不包括模仿言语的样本规模。栏Ⅳ（来自表4-3栏Ⅵ）是不同词语（序列）的数量，该数量与模仿言语是否包括在内依然一样。栏ⅤA和ⅤB是各自最佳Y斜率（负值，首先是包括模仿言语的那些样本的斜率，然后是不包括模仿言语的那些样本的斜率）。栏ⅥA和ⅥB分别首先为包括然后为不包括模仿言语的那些样本的Y误差。
我们在审视栏Ⅲ中两组样本规模时发现，总体而言，A和B两栏中相应数值之间的比例差异随着年龄增加越来越不明显。也就是说，随着儿童长大，其言语总量中模仿言语部分呈下降趋势，到了29个月大时规模言语几乎可忽略不计。此外，我们转至栏Ⅴ斜率和栏Ⅵ误差中A和B的个体数值时，我们再次发现相应数值之间的差异随着年龄增加越发不明显，这一点我们在随着年龄增长A和B栏中基本样本本身差异越来越少。的确，在到了28个月大时A和B的斜率差异比较起来如此微不足道以至于大概再作他谈毫无益处，只能说到28个月大时不包括模仿言语的B斜率与包括相应的模仿言语的A斜率总体来看要么是相同的要么前者仅仅稍小于后者。
直到27个月大时A斜率和B斜率之间的差异很明显。此外，在这些早先年龄群体中每种情况里A斜率都是比它们相应的B斜率要大些（陡峭些）。在所有17个样本中有6种情形（即编号为5、12、14、15、16和17的样本）里A斜率都是同样近似或更加近似于1；而且除了样本5之外，离22个月越近的样本，B斜率越是远离-1。
因此，如果我们根据实证研究认为负1斜率代表统一化之力与多元化之力之间的平衡状态，我们可以作此总结：不仅童年的“未成年非文化言语”而且童年的模仿言语不管怎样都构成了全部言语表达的动态整合部分。虽然这个结论既简单又明显，然而它带给我们一些理论思考，这些思考对于我们工具和最省力原则的相互经济的全部研究具有重要意义，尤其是当我们现在想知道所有这些曲线和数据可能具有什么意义时更加有价值。
第三节 言语“起源”的理论探讨
上述表4-2、4-3和4-4中的数据在一个重要方面是明确的：它们揭示了同等量值的儿童言语样本在序列—频率分布上可能一致，它们计算出的最佳斜率几乎都是-1。那么这就意味着两件事：首先，儿童选择和使用“词语”是遵从一条法则而不是任性变化的。其次，这条法则极有可能就是第二章中控制乔伊斯《尤利西斯》和埃尔德里奇语料中词语分布的同一条法则，结果是我们因而可以放心用经验方程式r×f=C及其推论方程式F·Sn加以运算（我们完全知道任何对此还有怀疑的人都完全可以根据本国成千上万个会说话的儿童的言语表达客观地检验我们的方程式）。但是这还未完。
表4-2、4-3和4-4中联合数据进一步揭示了儿童言语中两大要素，其中之一我们刚刚论及。它们已经表明了童年的“未成年非文化言语”和模仿言语两者都是儿童言语流的动态整体的一部分，也就是说它们的存在使得词语分布更加接近双曲线的分布。其次，它们在Sn规模变化中已经揭示了，某特定儿童（或某特定年龄群的儿童们）使用言语的方式就最优规模而言并非恒常不变。由于这两大要素对于我们总体目标很有意义，所以我们接下来将依次在A和B中分别加以论述。
一、模仿言语（Echolalia）与“汪汪”叫声
我们刚才已经说过，任何怀疑我们本章研究普遍有效性的人都完全可以诉诸进一步的客观检验。我们十分欢迎此类深入的客观检验，以至于在此概述这类检验恰好所需的一个理想实验方案，虽然我们这样做时主要还是围绕当前理论探讨的说教意义。
首先，我们假定这个实验方案的主要目的是研究所有年龄的儿童言语表达，包括那些甚至小于22个月的儿童。这一点不难办到，我们可以将儿童自发言语表达进行电气录音，不让他们知晓。我们在积累了各类儿童足够多的言语记录之后应当转而统计分析这些语料。
根据我们对儿童的总体经验，我们在由年龄较大儿童的言语表达追溯到年龄最小儿童的言语表达时有望发现两件事。首先，我们有望发现模仿言语的比例随着年龄群越来越年轻而逐渐增多。其次，我们有望发现“未成年非文化言语”的比例也会随着年龄的减小而增多，直到完全是“咕—咕—嘎”的婴儿状态，此时模仿言语是指重复纯粹的“未成年非文化言语”。总之，随着我们由童年追溯到最初的婴儿时期，我们应当有望发现一个越来越是普遍模仿言语的状态和一个“未成年非文化言语”的状态，此类状态远不同于幼犬或众多其他动物发出的高兴、疼痛或难以辨识的表达。
相反，如果我们从一个小婴儿开始观察他逐渐长大时的言语表达，我们应当有望发现与上述相反的结果，因为该婴儿的未成年非文化模仿言语一方面愈发变得更成人化和文化性的言语表达，而另一方面模仿言语与非模仿言语的比例整体上渐渐变小了，这一点非常不同于幼犬或其他动物，它们的表达在经过一定年龄之后似乎很少有什么明显改变[4]。
假如我们首先集中注意力关注言语的普遍经济，我们可能认为这位日益长大的婴儿逐渐掌握了一套指挥身边人干活的工具。或者，更精确地说，他的言语表达在将身边人用作实现目的的手段（即，将人用作社会工具）时愈发更加有效。当然，即便是早期童年的牙牙学语在将身边人用作社会工具时也是有效的；例如婴儿的哭泣与作为社会工具的母亲反应（以及常见的类似犬吠及其主人的反应）。的确，我们可以认为甚至在婴儿纯粹“生理的”哭泣也潜藏着普遍经济，虽然该婴儿或许并非总会知晓他从中获益的这种经济的存在及其本质[5]。因此，如果我们可以设想婴儿出生后扩展胸肺时无意识的“生理”哭叫已经在人类历史的一段时间内叫人们关注新生婴儿，然而从母体中生下来的遗腹子如果不哭叫很有可能不被发现，我们应当在这个方面有一个言语表达的例子，该言语表达在几乎所有幸存事物任务中都是无意识却是社会化完成的，此类幸存只要任何一个正式词语或句子即可完成。因此，言语的普遍经济即便是在纯粹无意识的噪声中也是潜存的。
我们现在从言语的普遍经济过渡到我们统一化之力与多元化之力所论述的言语内部经济时必须记住，我们从未将我们的讨论专门限定在正式成人词语的选择和使用上，以区别于婴儿牙牙学语或者任何其他手段有意或无意给身边人或身边任何其他事物表达一个“想法”或以另外方式激起一个反应。因此，我们可以推理，统一化之力与多元化之力在婴儿牙牙学语中至少也是潜存的，这就意味着，即便是婴儿有一个100%频率的单一“儿语词语”以及有n个“儿语词语”的一套儿语，都可能是经济节约的，这取决于要完成的言语任务的本质。
当然，随着儿童逐渐长大又遇到更加复杂的言语任务，他可能发现如果将儿语表述为正式类别（即词语）更加经济，后者作为陈规可被社会理解。这对于听者而言也会是更加经济（对于那些生物社会动力学专业学生们同样更经济，他们必须要给儿童言语分类）。因此，成年的正式词语，我们从中已经发现了双曲线关系，或许可视作只不过是组织为社会陈规的儿语，以便把身边人更有效地用作社会工具。
当然，如果儿童碰巧不需要把身边人用作社会工具，那么他也会发现为了这个身边人而将自己的儿语正式化没有任何经济性。而且，一般来说，个体将自己的“儿语”正式化如果超过了自己更加经济幸存的需要，这从来就不经济。因此，例如，一个成年人如果要成为一个工程师，那么知道logarithm（对数）这个不寻常的词对他来说就是经济的；但是对于一个泥瓦匠来说，就像一个新生婴儿一样，就没有必要知道这个词或者任何其他新词，除非他现有的“儿语陈规”储备不够任胜手头的工作。
婴儿随着自身的成长其任务也在增长，于是他们运用现有工具完成任务的能力显然也在增长，包括运用身边人这种工具的能力，身边人对于自我支撑、自我防卫和自我增殖的普遍任务而言是一个非常有用的社会工具。而且随着身边人越来越是幸存的经济型社会工具，愈发高度清晰表述的正式成人语言的“儿语”也自荐为一个更加经济型的工具，从而将身边人当作一个社会工具。因此，我们可以认为，总体而言，随着人的更加社会化，他的言语也变得更加社会化，这就意味着，其言语更加正式地固化进“成年人词语”（其他动物同样如此，比如狗和诸多鸟类，它们经常把叫声固化，引起同伴以某种差不多固化的方式作出反应）。
二、言语“起源”
上文讨论的婴儿儿语引发了言语起源这个陈腐问题，这个问题常常有几近明确的回答，却并非总是预先界定了起源和言语这两个术语。
如果言语意味着一个个体发出的任何一类噪声并引起了另一个个体的某个具体的反应（或联想），那么我们远祖中第一个将同伴的某个具体生理噪声与其另一类行动联系起来的人就是发现言语的第一人。因此，例如，如果多年前一个个体因为痛苦而发出了一个陈规化的叫声或者因为看见食物自发喜悦而扇动翅膀，而且如果同类中另一个体由此推断发生或即将发生什么行为，那么按照上述严格定义，言语就已经产生了。根据这个定义，咳嗽、打喷嚏、可听见的肠胃胀气、临终喉鸣等都是言语。这种观点基本上是言语“汪汪”论，而且所有叫声（或气味或手势）陈规化的动物都恣意于言语中。在后文章节中我们称此为物种语言，或生理语言。它是指几乎正确理解了无意识生理反应，如理解了怒犬狂吠。
另一方面，例如，一旦犬吠或竖起爪子是为了引起某种具体反应，而且如果该吠声或竖爪不是无意识生理行为的结果，假如任何其他个体对之作出正确理解，那么便产生了文化言语。因此，当这只狗叫起来是为了讨晚饭吃，而且其主人明白此状，那么这两个个体就有了共同的文化语汇（参见第七章），于是文化言语就已经出现了。
生理言语和文化言语之间的区别界线细微却很重要，因为一旦发出约定俗成的信号这个第二步产生了，那么在这单个约定俗成信号与人类最复杂精美的句法言语之间就没有动力差异，除了不同信号的数量n多少有动力差异之外。无论哪种情况下，言语总是意味着文化言语，发出的信号与引起的反应之间没有必然的生理联系。
至于文化言语的起源，我们只能说，我们远祖中第一个发出上述意义且被理解的约定俗成信号的人就是第一个说话的人。这发生在什么时候，恐怕永不为人知。但是没有理由认为，这是在我们祖先成为人类（无论那是什么时候）之前不久发生的事情。也没有理由认为，文化言语为人类独有。麻烦在于文化信号总有一天会成为无意识的生理行为（如，显然是无意识的ouch！绝不是普遍的人类疼痛信号）。蜜蜂的花粉舞假如不再是无意识行为可能起初就是文化言语。如果我们认为，任何有生命的社会体系的成员，借助类似规划共同协助追求类似目标，很可能从最初生理现象的分类中演变出一种文化语言，这也未免太草率了。
个体中人类言语“起源”的一个常用例子可见于小宝宝的哭叫。虽然这位婴儿最初哭泣只是因为肚子有点痛，然而当他发现他一哭妈妈就来了，那么他就发现了人类言语、一个词语和一个意义。几乎每个婴儿都已独立得出此类发现。难道我们能说就没有其他物种的后代曾经作出相应的发现吗？难道没有小猴子曾经朝它妈妈尖叫以便吸引她的注意吗？
无论如何，以上论述澄清了我们至少对于言语“起源”这个问题的本质的界定。在个体已经发现了第一个词语之后，扩大词汇的规模n就很容易，或许可以通过比如说桑代克在其儿语理论中主张的一类联想来扩大词汇。人类文化言语或许已经独立“起源”了许多次7。
在讨论物种言语“起源”时，童年言语起源显然十分有意义。
三、儿童言语的“重演法则”（the“Law of Recapitualtion”）？
研究言语“起源”多少可以通过阐明儿童言语历时分层来进行，这些儿童言语是以第三章的图3-10中成人言语使用的方式表述的。因此，例如，当一个儿童学会说话时他是否更偏爱使用文化语汇中更旧、更短的词语？正如根据所谓的生物“重演法则”有望预料的，个体据此法则在个体发育上往往重演其物种系统发育历史？[6]
为了研究这个问题，我先前的学生马歇尔·G.普拉特（Marshall G.Pratt）检测了下面三个儿童言语样本中词语采纳的数据：（1）表4-3的第45号样本所表示的36个月大的儿童联合言语，代表了总量为4 339个连续词语的481个不同词语；（2）总量为10 000个连续词语的五岁大的额尔布鲁克语料；以及（3）总量为10 000个连续词语的七岁大的额尔布鲁克语料。分析步骤与第三章历时言语层所用的相同。
至于定量呈现该数据，鉴于样本规模不一，比较起来有困难，因为（36个月）第一个样本只有（5岁和7岁）第二个和第三个样本规模的一半，而后者反过来只有埃尔德里奇语料的五分之一，埃尔德里奇语料的分层我们在图3-10中研究过了而且我们又将之呈现在图4-2中以便比较。
比较不同样本可能有好几个方法。因此，例如，我们可以将每个样本中序列词语的总量视作100%，再接着研究四个样本（包括埃尔德里奇的）中每个连续5%或10%的不同序列词语的历时分层。在此情况下，根据语料，年龄越小的儿童显然使用更旧（以及更短）词语的比例一定很多，这种比例在36个月大的语料中达到最大值。
一个更加保守的方针也是我们在图4-2中采用的是，将四个样本的每个样本中所有词语以100个序列词语为一组进行分组，然后对每个样本的连续各组词语进行历时分层比较。用这种更加保守的比较方法研究得出的任何历时分层百分比之间的差异，都十分有意义。
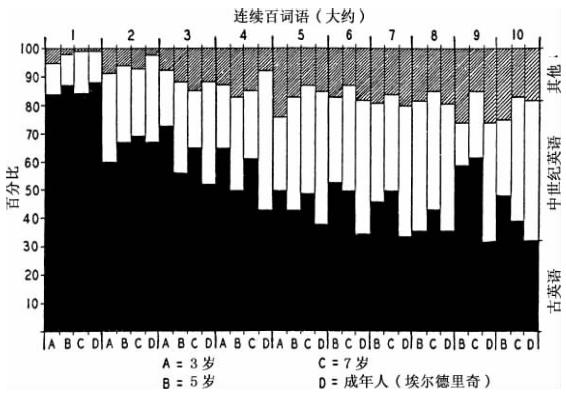
图4-2 不同年龄人言语的序列词语（以百词为单位）的文化——历时分层：（A）三岁；（B）五岁；（C）七岁；（D）成人（埃尔德里奇语料）。
图4-2中以一百个序列词语为单位依次绘制了——直至第10个百词，如果有现成的话——古英语和中古英语的历时分层百分比，以及所有后来的36个月大时语料A、五岁时语料B、七岁时语料C和埃尔德里奇语料D共同联合起来的历时分层百分比。这些只是近似值（如，图A的第5个百词代表的是仅有81个不同词语的百分比，而不是100个词语的）。当某特定百词语包括一个或两个不同整数频率类别的分数时（如，第8个百词组可能包括了部分出现8次的那些词语的分数和那些出现3次的词语的分数），我们计算的是所讨论的全部整数频率类别的分层百分比；这些百分比也被指定用于那些包括（各种）整数频率类别的（不同）分数部分的百词组。
我们在审视图4-2时发现，前两个百词组的历时分层百分比没有什么差别，好像即便是小孩子们也会说出那些冠词、代词、助动词、介词等等，而且基本上是以成人的频率使用这些词语。但是从第3个百词组开始，D栏埃尔德里奇语料在所有情况下使用的古英语词语的百分比都小于其他语料。此外，三岁时语料图A在所有情况下使用的古英语词语的百分比都是最大的，除了在第1个和第2个百词组中不是最大。图B和C的变化使得它们的古英语层很难作任何比较。此外，在所有四个样本里中古英语与“其他层”英语的百分比之间似乎没有什么显著差异。
根据这些为数不多的数据我们可以在多大程度上加以概述，这还是个问题，我们只能概述我们大家已经预料的：儿童年龄越小，言语中使用的更旧、更短词语的比例越大。然而这种简单的说法却表明了，更加广泛地分析儿童言语历时层对于阐明“重演法则”可能具有重要意义。
乘我们还在讨论儿童言语表达这个主题的时候，以及还在讨论年龄大的小孩子们可能倾向使用略微愈发更多比例的更长更新词汇，我们提请大家关注玛丽·沙托克·费希尔博士以及其他人对于儿童言语结构的精彩研究8。多亏他们的研究，我们知道，一般来说，所用句子的长度和复杂程度随着儿童年龄的增加而增加，甚至词汇的丰富多样也是如此；所有这一切都可以根据第三章论述在理论上能够预见到。同样有趣的发现是，词语I（我）的相对频率往往随着儿童年龄增长而减小，因为他更加习惯并且关注群体及其共同社交中其他参与者的存在。
第四节 小 结
本章大部分内容呈现了儿童言语表达的实证数据，我们从中发现了从22个月大到七岁时的全部研究中存在着调和法则的比例。
然而，这里所说的调和分布，是指所研究的全部儿童言语表达，包括模仿言语和无意识的非文化表述（文理不通的话语），这类表述在年龄越小的儿童言语中数量越多。诚然，排除模仿言语（以及文理不通的话语，这可以推论出）之后，调和分布的近似值也就不存在了。因此，我们归纳出，童年的模仿言语和文理不通话语是儿童全部言语表述的一部分，随着岁月流逝儿童行为也愈发约定俗成或文明化之后，这部分言语也逐渐消失。如果这个结论是正确的，那么我们认为社会群体文化的约定俗成是行动词汇的一个选择，这种约定俗成取代了早期的个体行动词汇，却没有改变基本动力原则。
至于言语“起源”这个迂腐问题，我们已经提示有必要界定这些术语。如果言语是指生理言语，即解读他者明显无意识的生理行为，甚至是我们根据经验解读非生物界的行为（如，狗对于雷暴气象的反应），那么言语就是如同生命一般久远。但是如果言语是指文化言语，即意味着发出一个约定俗成的陈规化噪声为了引起另一个体约定俗成的陈规化反应，而且该类行为与该类反应之间没有必然的生理联系，那么我们先祖中第一个发出尖叫声想要告诉其母或其妻自己所在位置的人，就是第一个说话的人，这时只有1个词语指定到方程式F·Sn=1。在这位个体已经迈出第一步使n=1文化词语存在其词汇中之后，n值就能根据第三章论述的那些原则继续增加。
显然，在儿童言语发展中，语言里更旧、更短词语的比例呈下降趋势，这一点我们可以根据生物学“重演法则”预料到。
[1]我们不会陈述有关词语重复之间间隔大小分布的信息（Nf·S=常量），不仅是因为作此分析任务繁重，而且更特别的是因为这个方程式对于研究人格差异特别有用（正如我们在第二章末尾讨论不平衡的那个案例时发现的），而我们目前对于人格差异研究没有兴趣。对于我们当前目的，调和方程式就足够了。
[2]就直线的弯曲这个问题而言，——这个问题我们将在后文章节中不断论及——我们目前可以认为，这位儿童在其有限话语中使用了成人词语，因而表明了其间存在的稚嫩，这一点可以理解。
[3]然而我们必须记住，总体而言，我们理论上的Sn将会随着斜率而变化；因此，随着斜率增加，理论F值不仅也在增加而且还代表了连续词语总数Σ的更大部分；因此，如果Σ是个常量，斜率的减少即意味着Sn的减少。
[4]如果我们将一群不同年龄儿童的Sn的Y-数值绘制成图对应他们各自的X-年龄，并且拟合成一条曲线，有意思的是，我们是否会发现计算出的X-截距更近似于0月数或-9月数。
[5]我们在此仅顺便提及行动与概念之间的整个关联问题，这个问题的精彩研究成果有巴甫洛夫（I.P.Pavlov）、亚当斯（D.K.Adams）、赫尔（C.L.Hull）、乔治·汉弗莱（George Humphrey）、桑代克（E.L.Thorndike）、瑟斯顿（L.L.Thurstone）等其他人所作的。恩斯特·R.希尔加德（Ernest R.Hilgard）最近出版了一部颇有价值的有关主要学习理论评论分析，并附有相当全面的参考文献6。
[6]该主题将在第六章详细论述。
