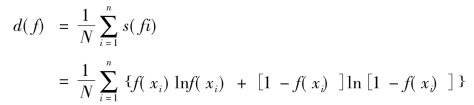-
1.1总 序
-
1.2绪论 人际沟通:信息的传递与交流
-
1.2.1一、沟通与人际沟通
-
1.2.2二、信息交流的必要性与人际沟通的必然性
-
1.2.3三、人际沟通的基本特点
-
1.2.4四、人际沟通的形式
-
1.2.5五、人际沟通的信息学模型
-
1.3第一章 信源与信宿:人际沟通的主体
-
1.3.1第一节 人际沟通主体及其一般结构
-
1.3.1.1一、人际沟通主体的基本含义
-
1.3.1.2二、人际沟通主体的一般结构
-
1.3.2第二节 作为人际沟通主体的信源
-
1.3.2.1一、信源——沟通主体Ⅰ
-
1.3.2.2二、信源的能力素质
-
1.3.2.3三、信源的心理特征
-
1.3.3第三节 作为人际沟通主体的信宿
-
1.3.3.1一、信宿——沟通主体Ⅱ
-
1.3.3.2二、信宿的能力素质
-
1.3.3.3三、信宿的心理特征
-
1.4第二章 信息:人际沟通的内容
-
1.4.1第一节 信息的本质
-
1.4.1.1一、信息的基本含义
-
1.4.1.2二、信息与物质及能量的关系
-
1.4.2第二节 信息的特征
-
1.4.2.1一、普遍性
-
1.4.2.2二、传递性
-
1.4.2.3三、共享性
-
1.4.2.4四、有用性
-
1.4.2.5五、寄载性
-
1.4.2.6六、时效性
-
1.4.2.7七、开发性
-
1.4.2.8八、无限性
-
1.4.2.9九、滞后性
-
1.4.3第三节 信息的分类
-
1.4.3.1一、社会信息与非社会信息
-
1.4.3.2二、客观信息与主观信息
-
1.4.3.3三、实在信息、先验信息与实得信息
-
1.4.3.4四、直接信息与间接信息
-
1.4.3.5五、言语信息与非言语信息
-
1.4.3.6六、内储信息与外化信息
-
1.4.3.7七、动态信息与静态信息
-
1.4.3.8八、可外传信息、不可外传或只可在极小范围内传递的信息
-
1.4.3.9九、有记录信息与无记录信息
-
1.4.3.10十、有用信息与无用信息
-
1.4.3.11十一、实质信息与冗余信息
-
1.4.3.12十二、空壳信息、黑洞信息、饱和信息与含熵信息
-
1.4.4第四节 信息的层次
-
1.4.5第五节 信息的度量
-
1.4.5.1一、不定性与信息量
-
1.4.5.2二、度量信息的方法
-
1.4.6第六节 信息的作用
-
1.4.6.1一、信息是人类生存的前提
-
1.4.6.2二、信息是人类社会发展所必需的资源
-
1.4.6.3三、信息是人类一切智慧和知识的源泉
-
1.4.6.4四、信息是人类社会各种管理活动有序开展的必要手段
-
1.5第三章 符号:人际沟通信息的载体(上)——符号概论
-
1.5.1第一节 符号的基本含义
-
1.5.1.1一、符号的定义
-
1.5.1.2二、符号研究的历史考察
-
1.5.1.3三、符号与信号
-
1.5.1.4四、符号、消息、信息
-
1.5.2第二节 符号的特征
-
1.5.2.1一、形式与内容的统一
-
1.5.2.2二、约定性与任意性的统一
-
1.5.2.3三、稳定性与可变性的统一
-
1.5.2.4四、系统与要素的统一
-
1.5.3第三节 符号意义
-
1.5.3.1一、意义概述
-
1.5.3.2二、几种有代表性的意义理论
-
1.5.3.3三、意义的基本种类
-
1.5.4第四节 符号与人际沟通
-
1.5.4.1一、人际沟通是符号存在和运用的基础
-
1.5.4.2二、符号是人际沟通的前提条件
-
1.5.5第五节 符号的基本类型
-
1.5.5.1一、符号分类概述
-
1.5.5.2二、两大沟通符号系统及其相互关系
-
1.6第四章 符号:人际沟通信息的载体(中)——言语沟通符号
-
1.6.1第一节 言语沟通符号概述
-
1.6.2第二节 言语沟通符号的基本特征
-
1.6.2.1一、社会性
-
1.6.2.2二、随意性
-
1.6.2.3三、线条性
-
1.6.2.4四、开放性
-
1.6.2.5五、规则性
-
1.6.2.6六、概括性
-
1.6.2.7七、组装性
-
1.6.2.8八、复杂性
-
1.6.2.9九、超时空性
-
1.6.2.10十、解释性
-
1.6.2.11十一、习得性
-
1.6.3第三节 言语沟通符号的种类
-
1.6.3.1一、言语沟通符号的两大基本类型
-
1.6.3.2二、两种言语沟通符号各自的优点和缺陷
-
1.6.4第四节 模糊性言语沟通符号及其科学分析
-
1.6.4.1一、模糊性言语沟通符号的存在依据
-
1.6.4.2二、模糊性言语沟通符号的类型分析
-
1.6.4.3三、模糊性言语沟通符号在人际沟通活动中的作用
-
1.7第五章 符号:人际沟通信息的载体(下)——非言语沟通符号
-
1.7.1第一节 非言语沟通符号的基本概念
-
1.7.2第二节 非言语沟通符号的特点
-
1.7.2.1一、总成性
-
1.7.2.2二、传承性
-
1.7.2.3三、习惯性
-
1.7.2.4四、心理性
-
1.7.2.5五、转换性
-
1.7.2.6六、功利性
-
1.7.2.7七、民族性
-
1.7.2.8八、共通性
-
1.7.2.9九、模糊性
-
1.7.2.10十、语境依赖性
-
1.7.3第三节 非言语沟通符号的分类
-
1.7.3.1一、动姿沟通符号
-
1.7.3.2二、静姿沟通符号
-
1.7.3.3三、情态语沟通符号
-
1.7.3.4四、触摸语沟通符号
-
1.7.3.5五、近体学沟通符号
-
1.7.3.6六、标志语沟通符号
-
1.7.3.7七、辅助言语沟通符号
-
1.7.3.8八、类语言沟通符号
-
1.7.4第四节 非言语沟通符号的基本功能
-
1.7.4.1一、替代功能
-
1.7.4.2二、强化功能
-
1.7.4.3三、表达功能
-
1.7.4.4四、印证功能
-
1.7.4.5五、补充功能
-
1.7.4.6六、调控功能
-
1.7.5第五节 非言语沟通符号的文化差异
-
1.8第六章 编码:人际沟通信息的构织
-
1.8.1第一节 编码概述
-
1.8.2第二节 编码的基本原则
-
1.8.2.1一、完整准确性原则
-
1.8.2.2二、码解唯一性原则
-
1.8.2.3三、码位简洁性原则
-
1.8.3第三节 编码的基本要求
-
1.8.3.1一、对象要求
-
1.8.3.2二、策略要求
-
1.8.3.3三、角色要求
-
1.8.3.4四、美学要求
-
1.8.3.5五、文化要求
-
1.8.3.6六、时代要求
-
1.8.4第四节 编码过程简析
-
1.8.4.1一、编码的计划阶段
-
1.8.4.2二、编码的执行阶段
-
1.9第七章 解码:人际沟通符号的破译
-
1.9.1第一节 解码及其基本类型
-
1.9.1.1一、解码的基本概念
-
1.9.1.2二、解码的基本类型
-
1.9.2第二节 解码的前提条件
-
1.9.2.1一、建立一个“公共信号库”
-
1.9.2.2二、正确地利用语境
-
1.9.3第三节 解码的过程分析
-
1.9.3.1一、解码的感知阶段
-
1.9.3.2二、解码的理解阶段
-
1.10第八章 噪音:人际沟通的障碍
-
1.10.1第一节 人际沟通噪音及其分类
-
1.10.1.1一、噪音与人际沟通噪音
-
1.10.1.2二、人际沟通噪音的分类
-
1.10.2第二节 常见人际沟通噪音及其克服对策
-
1.10.2.1一、生理学噪音及其克服对策
-
1.10.2.2二、心理学噪音及其克服对策
-
1.10.2.3三、物理学噪音及其克服对策
-
1.10.2.4四、语言学噪音及其克服对策
-
1.10.2.5五、社会学噪音及其克服对策
-
1.10.2.6六、文化差噪音及其克服对策
-
1.11结语 关于人际沟通信息学的若干思考
-
1.11.1一、建立人际沟通信息学的必要性与可能性
-
1.11.2二、人际沟通信息学的内容和任务
-
1.12参考文献
-
1.13后 记
1
人际沟通学
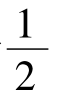 ,状态x
,状态x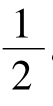 。再比如,投掷均匀正六面体骰子,具有六种同样可能的状态,即状态y
。再比如,投掷均匀正六面体骰子,具有六种同样可能的状态,即状态y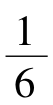 。在这种情况下,当然,掷六面体骰子的不定性大,为了消除它的不定性,掷骰子场合所需要的信息应该比掷硬币场合多。但是,如果骰子不是各面同重,而是其中的一面特别重,那么,投掷的结果往往是出现某一特定的点数,比如这时有:
。在这种情况下,当然,掷六面体骰子的不定性大,为了消除它的不定性,掷骰子场合所需要的信息应该比掷硬币场合多。但是,如果骰子不是各面同重,而是其中的一面特别重,那么,投掷的结果往往是出现某一特定的点数,比如这时有: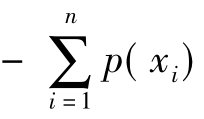 =1,那么,该事物所具有的不定性数量H(x)为:
=1,那么,该事物所具有的不定性数量H(x)为:
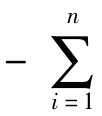 p(x
p(x
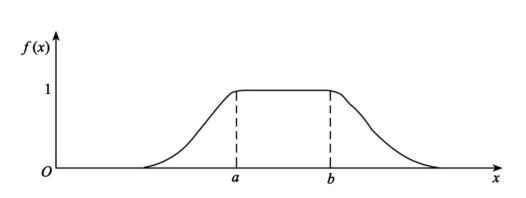
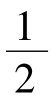 时,μ(f)=max;
时,μ(f)=max;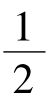 ,有f
,有f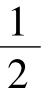 ,有f
,有f