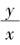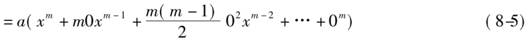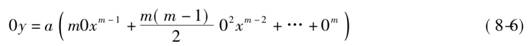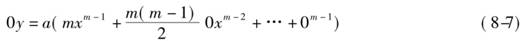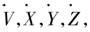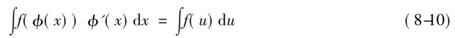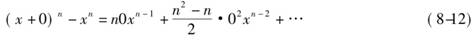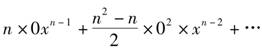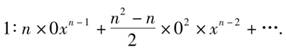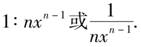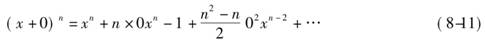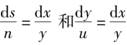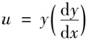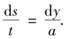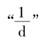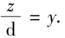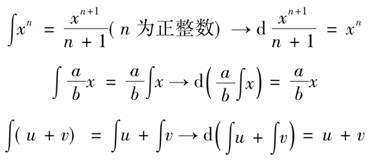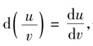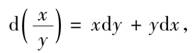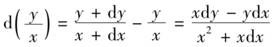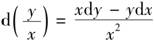§8.2 微积分的创立与发展
解析几何的创立，将变量引进了数学．使运动与变化的定量表达式成为可能，从而为微积分的创立搭起了舞台．微积分的萌芽，特别是积分学部分可以追溯到古代，比如面积和体积的计算自古以来一直是数学家们感兴趣的课题．在古希腊、中国和印度数学家们的著述中，不乏用无限小过程计算特殊形状的面积、体积和曲线长的例子．而阿基米得、刘徽及祖冲之父子等人的方法及工作，确实体现了他们是人们建立一般积分学的漫长努力的先驱．
近代微积分的酝酿主要是17世纪上半叶，其主要代表人物当属牛顿和莱布尼茨两人．
8.2.1 牛顿及其微积分思想
1.“圣诞老人”的儿子——艾萨克·牛顿
牛顿(Isac Newton，1642～1727)于伽利略去世那年——1642年的圣诞节出生于英格兰林肯郡一个农民家庭．在他出生前，其父老艾萨克就去世了．留下牛顿的母亲，汉那·艾斯库·牛顿，一个怀孕的寡妇．那年圣诞节牛顿刚生下来的时候，他是那么的瘦小和虚弱．据说可以放进一个一夸特的啤酒杯里．没有人料到他能活得过当天，可是他活下来了，还长成足够健壮的身体，活过了80岁．
牛顿
图8-4
牛顿3岁时母亲改嫁给一位63岁，姓史密斯特的牧师．牛顿大约5岁入小学，1655年，入英格兰瑟姆中学读书．少年的牛顿于孤独中成长，他不是一个神童，在校成绩并不突出，但他喜欢读书，自中学起就有作读书笔记的习惯．中学时代的牛顿，在做机械模型和实验上显示了他的爱好和才华．
牛顿到了17岁的时候，他的母亲把他带回伍尔索普的农庄，协助她经营那块小农田，过了一年，以后在其舅父的帮助下又入学读书．1661年，牛顿19岁，以优异的成绩考入剑桥大学的三一学院接受更高深的教育，那是他舅舅读书并获得硕士学位的地方，那是一所历史悠久，产生许多学者和政治人物(如牛顿、克伦威尔、弥尔顿、达尔文、罗素、凯恩斯和现代的霍金，而霍金现任的职位，正是当年牛顿所担任的讲座教授)声誉卓著的学校．
牛顿在三一学院当学生时的社会地位只是一个次工读生，是要替别的学生做卑微的工作，以赚取生活费的．一般尚存有阶级意识的社会里，在学生餐厅中，次工读生的地位是先服务其他学生用膳，等到其他学生用过之后，剩余的饭菜，才轮到他们享用．牛顿并非因家里太穷而被迫分进这个最低下的学生阶层，他成为一个次工读生，是因为母亲不愿意提供让他处身较高阶层的费用．
在牛顿上大学之前，一直没有把注意力放在数学上，因此，上大学后，他先读欧几里得的《几何原本》，在他看来太显然了．然后看笛卡儿的《几何学》，对他来说，又有些困难．他从读数学转到研究数学．早在1665年他才23岁毕业前夕，就知道推广的二项式定理，这是他数学生涯中的第一个创造性成果．并且创造了他的流数法(现在我们称之为微分学)，同年，获得文学学士的学位，并当了研究生．但不久便由于伦敦流行鼠疫，大学停课，牛顿只好回农村居住，一住就是18个月．在这个时期，他把他的微积分发展到能求曲线的任意一点的切线和曲率半径．他还对许多物理问题感兴趣，做了他的第一个光学试验，并且把他的万有引力理论的基本原则系统化了．这一时期，牛顿的两大发明：微积分，万有引力定律都成为了科学史上的重大成就，其中单独任何一项都能够让他名垂青史．他在追忆这段峥嵘岁月时说：“当年我正值发明创造能力最强的年华，比以后任何时候更专心致志于数学和哲学(科学)．”1666年，牛顿完成了《流数简论》的论文，1669年，牛顿完成了第二篇讨论流数的论文．这个流数法，就是现在的微积分．虽然他没有发表这些论文，但是他让人看过，足以支持他宣称自己为第一个创造微积分的人．尽管莱布尼茨最先发表自己的微积分．
1667年，牛顿回到剑桥，不久当选为三一学院的研究员．两年之后，1669年10月，由于他在科学上的出色成就，他的老师巴罗主动把数学教授的职位让给他．从此，牛顿开始了他30年的大学教授生活．
其间，牛顿将他大部分时间都埋头于他的研究．他把自己的房间改建成了一个精巧的实验室，能够不分昼夜地在那儿做实验．1672年，他发表了一篇论文，提出他的颜色理论，受到了一些有影响的科学家的猛烈攻击．牛顿看到随之而来的争论很无聊．就发誓再也不发表任何关于科学的东西．
除了数学和万有引力理论两项成就外，他还制造了第一架实际可用的反射式望远镜．他把这架望远镜送给皇家学会，学会收到之后，很快就选他为院士，此后他终其一生都是院士，最后又担任皇家学会主席．
由于牛顿在三一学院的地位及对皇家学会的影响，1687年，在他担任卢卡斯数学讲座教授18年之后，著名天文学家哈雷(Edmund Halleg)终于说服牛顿发表他的理论．这部书就是《自然哲学的数学原理》，如今简称《原理》，成为他科学学术生涯的最高成就．
在这部书中，牛顿详细地说明了他的万有引力理论，也谈到了他的流数法以及微积分基本理论，书中还包含理论力学和流体力学，以及开普勒行星运动定律的数学推导．这些理论能够解释地球、太阳和行星的质量，地球在赤道略鼓出的原因，潮汐的理论等．总之，著名的牛顿力学三大定律，万有引力定律及牛顿的微积分成果都载于其中．在一部书里同时容纳这些东西，是一件了不起的成就．这本书像飓风一般席卷整个科学世界，立刻把牛顿推到科学界的最高阶层．
由于长期的紧张工作和母亲病逝的精神打击，牛顿得了精神衰弱症．1693年，牛顿写成了他的最后一部微积分专著《曲线求积术》，这也是牛顿最成熟的微积分著作．
1696年，牛顿离开剑桥大学迁往伦敦，他被任命为英格兰造币厂的厂长——那是一个相当重要的职位．在担任厂长职位后，起先还以请假缺席方式，保留卢卡斯讲座教授的职位．然而到了1701年，他终于放弃了在剑桥的讲座．那可能是由于他在那一年当选为国会议员而促成的．
为了表彰牛顿担任造币厂的厂长时的功绩以及他在科学上的地位，1705年，牛顿受封为爵士．此时，他达到了一生成就的最高峰，然而牛顿依然能写出一些富有意义的作品．1704年，牛顿完成了《光学》一书．但他的晚年研究重心——却逐渐转移到了化学、炼丹和神学，再由于与莱布尼茨的不幸争论很不愉快，于1727年，在一场拖了很长时间的痛苦的病后去世．终年85岁．
2.牛顿的微积分思想
微积分的创立，并不像解析几何的创立那样传奇．如前所述，从古希腊的阿基米得、中国的刘徽、祖冲之，法国的费尔马、笛卡儿，英国的巴罗等均为微积分的创立作出了重要的贡献．但是微积分学说终究不是各种特例及其方法堆积而成的，发现微积分的有关方法是一回事，而对这些方法加以提炼，使之一般化，则是另一回事．在牛顿和莱布尼茨之前的一个世纪里，曾经出现过不少极其成功的富有启发性的方法，但始终没有人在这些方法的启发下构思出真正属于微积分的概念，最好的例子就是构造切线．尽管有很多微积分先行者冥思苦想地创造出一个又一个确定切线的具体方法，但却没有一个人从中引出导数的概念及其一般规则，问题是他们“看不到要完成的是一个伟大的发现而恰恰又正在完成它．”自觉地意识到要完成一个伟大的发现，并实际去完成它的是牛顿和莱布尼茨．
如前所述，牛顿是一位科学巨匠，被誉为近代自然科学的伟大旗手．他以其在数学、力学、天文学、光学中的卓著成就，开创了近代自然科学的许多领域．仅在数学的研究方面，就涉及到数论、高次代数方程、解析几何、数值分析、概率论、曲线分类、变分法等问题．其最突出的贡献是他独立地创立了微积分．牛顿对微积分问题的研究始于1664年，当时他反复阅读了笛卡儿的《几何学》，对笛卡儿的求切线的“圆法”发生兴趣并试图寻找更好的方法，从而开始探讨微积分．牛顿在微积分方面的工作，大致可以分为四个时期：(1)流数概念的引入时期，这时他以运动学为背景引入了流数的概念，但未说明使用流数这个名字．与此同时，建立并推导了微积分的基本定理．(2)运用了变量x的无穷小瞬时期，这时他利用“瞬时”的概念，不仅给出了求一个变量对另一个变量的瞬时变化率的普遍方法，而且进一步证明了微积分的基本定理．(3)流数法的确立时期，流数法是他系统地应用第一时期引入的流数概念的结果，又是对第二时期应用静态无穷小的方法的再发展．这时牛顿把流数的概念从原来借助于运动物体的速度的解释发展到成熟的阶段．(4)牛顿所谓的最初比和最终比的确立时期，这时牛顿决定抛弃无穷小方法，代之以相当于函数增量与自变量之比的极限方法，因而成为极限方法的先导．
牛顿的微积分思想主要体现于下面几部作品中：
(1)《流数简论》，自从1664年萌发微积分想法之后，1665年夏至1667年春，牛顿在家
乡躲避瘟疫期间，继续探讨微积分并取得突破性进展．据牛顿自述，1665年11月，发明“正流数术”(微分法)，次年5月又建立了“反流数术”(积分法)．1666年10月，将其前两年的研究成果整理成一篇总结性论文，以《流数简论》著称．当时虽未正式发表，但在同事中传阅．因此《流数简论》是历史上第一部系统的微积分文献．
《流数简论》反映了牛顿微积分的运动学背景．论著事实上以速度形式引进了“流数”(即微商)的概念．牛顿在坐标系中通过速度分量来研究切线．促使了流数的产生．又提供了流数的几何应用的关键．牛顿把曲线f(x，y)=0看做沿x轴运动的点A和点B，他把点A，点B随时间变化的“流动速度”称作“流数”．牛顿创立了用字母上加一点的符号表示流动变化率．为此，他提出了两大问题：
1)设有两个物体x，y之间的关系．f(x，y)=0，求流数x，y之间的关系．
2)已知线段x和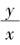
(即切线斜率)之间的关系，求x，y之间的关系．
牛顿首先确定所求面积对横坐标的变化率，再通过“反微分”求出面积．这种做法表明了求积问题与切线问题的互逆关系，它们是一个问题的两个方面．
(2)《运用无穷多项方程的分析学》，该论著1669年完成，1711年发表．在该论著中，牛顿的微积分思想在(1)的基础上有了进一步的发展．其表现在以下四个方面：一是牛顿把变量的无限小增量叫做“瞬”；二是牛顿采用了先除无穷小量再略去含有无穷小的项；三是计算中应用了二项式展开式，这使他的方法能适用于更广泛的函数；四是牛顿考虑了面积的瞬时增量，然后通过逆过程求出面积．
例如，设有一条曲线y，曲线下的面积为
z=axm(m为有理数) (8-4)
当横坐标x获得一个无穷小增量，即瞬“0”时，则z有增量
z+0y=a(x+0)m(按二项式展开)
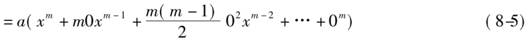
考虑到z=axm，得到
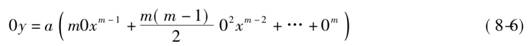
式(8-6)除以无穷小量0，得
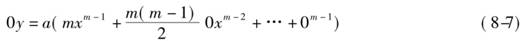
在式(8-7)中略去含有0的项，得
y=amxm－1 (8-8)
这就是相应于面积z的纵坐标y的表达式．该结果表明，面积在点x的变化率是曲线在点x处的y的值．反之，如果曲线是y=maxm－1，那么，该曲线下面的面积就是z=axm．在这里，牛顿不仅给出了求一个变量对于另一个变量的瞬时变化率的普遍方法，而且通过证明面积可以由求变化率的逆过程得到，揭示了微积分的基本性质．
与《流数简论》相比．《运用无穷多项方程的分析学》的另一项理论进展表现在定积分上．牛顿把曲线下的面积看做无穷多个面积之和．这种观念与现代的数学观念是接近的．为了求某一个子区间确定的面积即定积分，牛顿提出了如下方法，先求出原函数，再将上、下限分别代入原函数而取其差．这就是著名的牛顿—莱布尼茨公式．该公式是牛顿与莱布尼茨各自独立发明的．采用现代数学记号，设F(x)是f(x)在区间［a，b］上的一个原函数，则
有式(8-9)，在实际问题中应用极广的定积分计算问题便转化为求原函数问题，所以式(8-9)是十分重要的．
应该说，到此为止，牛顿已经建立起比较系统的微积分理论，但该理论的逻辑基础还是十分松散的．在计算中对无穷小量，即瞬0的似零非零的处理，说明牛顿对无穷小量的本质尚未作出明确的规定．对此，1734年，英国大主教贝克莱对牛顿的微积分进行了强烈的抨击，并由此导致了第二次数学危机(前文已述)．
(3)《流数法和无穷级数》，这是牛顿于1671年完成的第二部微积分学的代表作，并在1736年发表．在前两部论著的基础上，牛顿提出了更加完整的理论．表现在①引入了他的独特的概念和符号．②他将随时间变化的量，即以时间为独立变数的函数称为流数．以字母表中的几个字母v，x，y，z表示；而把变量的变化速度，即变化率称为流数．或简称为速度．记做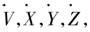
等．在该书中，还引入了强有力的代换积分法(用现代的符号)，设u=φ(x)，则
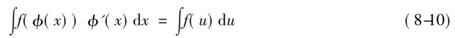
数学史上通常把牛顿的微积分方法叫做流数法．牛顿充分认识到这个方法的普遍意义，并明确指出：“流数法”不仅可以用来作出任何曲线和切线，而且还可以用来解出关于曲度(曲率)、面积、曲线长度、重心等深奥问题．牛顿的这个认识远远超过费尔马、巴罗等微积分先驱学者．正因为此，史称牛顿是把微积分作为一种普遍有效的计算方法的第一人．
(4)《曲线求积术》，这是牛顿的第四部代表作．写于1691～1693年，在这部论著中，牛顿为了排除无穷小量，引入了最初比与最后比的概念(或称为首末比方法)．《曲线求积术》是牛顿最成熟的微积分著作，在其中牛顿改变了对无限小量的依赖并批评自己过去那种随意忽略无限小瞬的做法：“在数学中，最微小的误差也不能忽略，……在这里，我认为数学的量不是由非常小的部分组成的，而是用连续的运动来描述的”．并在此基础上定义了流数的概念．
例如，求函数y=xn的流数，设x“由流动”而成x+0，于是xn就相应地变成
两边减去xn，得
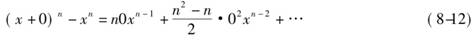
这个量表示，对应于x变到x+0，xn所发生的变化，用现在的话说，就是当x获得增量0后，xn所获得的增量，为了略去含有0的项，牛顿设想出了考虑x和xn的增量比．即0与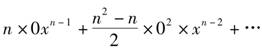
之比，这个比等于：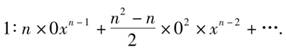
当增量消失时，它们的最后比就是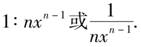
这个比不是别的，正是x的流数与xn的流数之比，亦即xn变化的比率．用现在的话说，这个比是xn关于x的变化率——导数．只是在形式上与今天的相倒置，今天y=xn的导数是y'=nxn－1．
虽然牛顿的微积分与现代微积分在概念的严格表述和理论的系统性、完整性方面，存在着许多差别，但是，正如《曲线求积术》所表述的，牛顿试图以正数为考察对象，以导数为中心概念，并把这类对象及概念奠定在极限基础上的做法，正确地反映了微积分发展的最终方向．
牛顿说：“如果我看得更远些，那是因为我站在巨人的肩膀上．”
8.2.2 莱布尼茨及其微积分思想
1.关于莱布尼茨——他本身就是一个科学院
莱布尼茨
图8-5
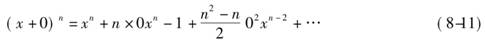
莱布尼茨(Gottfried Wwilhelm Leibniz，1646～1716)是德国著名的哲学家、数学家、自然科学家，17世纪伟大的全才．在微积分的发明上是牛顿的竞争者．于1646年出生于莱比锡城，出身书香门第，父亲是莱比锡大学哲学教授．耳濡目染，使莱布尼茨从小就十分好学．有人认为，莱布尼茨可能是最后一个真正的通才，还是儿童时就自学拉丁文和希腊文，15岁就进入莱比锡大学读书，他的学习课程涵盖广泛，包括法律、哲学、数学、逻辑学、科学、历史、神学等．莱布尼茨和牛顿一样是个天才，每门功课似乎都特优．莱布尼茨在莱比锡大学广泛阅读了F·培根(Bacom)，J·开普勒(Kepler)，G·伽利略(Galileo)等人的著作．1663年，莱布尼茨获得学士学位．同年转入耶拿(Jena)大学，并在魏格尔(E.weigel)指导下系统学习了欧几里得几何，1664年，获得哲学硕士学位．三年后，又获得法学博士学位，1669年，开始思考自然哲学问题．1672年，莱布尼茨进入外交界，担任过几个不同的外交职务，最后定居在汉诺威城邦．外交事务需要他在欧洲到处旅行，他就利用机会接触当时一些伟大的科学家、哲学家和数学家，包括惠更斯，在惠更斯(C.Huygens，1629～1695)等人的影响下，他对自然科学特别是数学产生了浓厚的兴趣，真正开始了他的学术生涯．1672年，莱布尼茨作为外交官出使巴黎．1673年4月，被推荐为英国皇家学会的外籍会员．莱布尼茨滞留巴黎的四年时间，是他在数学方面的发明创造的黄金时代，在这期间，他研究了费尔马、帕斯卡、笛卡儿和巴罗等人的数学著作，写了大约100页的《数学笔记》，这些笔记虽然不系统，且没有公开发表，但其中却包含着莱布尼茨的微积分思想、方法和符号，这些思想、方法和符号是他发明微积分的标志．
1676年，莱布尼茨返回德国，在汉诺威的职责是担任汉诺威公爵的历史顾问兼图书馆馆长，引发他在这两方面课题中写作许多有分量的著作．莱布尼茨发表过讨论地质学的精确理论，那是最早解释化石的企图之一．莱布尼茨提议使用人口动态统计来处理公共卫生问题，他首创语言科学，他研究心理学，最早提出“潜意识理论”的概念．1682年，莱布尼茨在自己创办的拉丁文杂志《博学学报》上首次发表了微积分论文《对有理量和无理量都适用的，求极大值和极小值以及切线的新方法，一种值得注意的演算》，这是莱布尼茨在微积分方面的代表作．
在科学方面，莱布尼茨贡献出动能的概念，他既是工程师，又是通讯师，他为银矿的排水设计抽水机，又设计夏宫里面的大花园，所有这些都是莱布尼茨在独立发明微积分之外的成就．
莱布尼茨去世后，遗留下堆积如山的未发表手稿，其中许多到今天还没有出版．1700年，莱布尼茨创建了柏林科学院，并担任首届主席．莱布尼茨和牛顿有许多共同点．有些方面的相同或相似令人惊讶，他也协助他的国家进行钱币改造等，监督汉诺威的造印厂；他有一双灵巧的手，亲手制作了一台计算机，这台计算机不仅能做加、减法，还能做乘、除法．莱布尼茨于1673年去伦敦旅行时，带了一台计算机到皇家学会表演，事后立即获选为院士．
1713年，维也纳皇帝授予莱布尼茨帝国顾问职位，并封他为男爵，邀请他指导建立科学院．莱布尼茨还建议成立圣彼得堡科学院，这些建议都被采纳了．莱布尼茨的科学远见和组织能力，有力地推动了欧洲科学的发展．他甚至写信给中国的康熙皇帝，建议成立科学院．
莱布尼茨是受中国学术界重视的人物，他是第一位全面认识东方文化尤其是中国文化的西方学者，他系统地阐述二进制数并把二进制数与中国的八卦联系起来，为东西方科学文化的传播与交流做出了自己的贡献．莱布尼茨强调，中国与欧洲位于世界大陆东西两端，都是人类伟大灿烂文明的集中地，应该在文化、科学方面互相学习、平等交流．
莱布尼茨一生没有结婚，1716年11月14日，莱布尼茨平静地离开了人世．享年70岁．
2.莱布尼茨的微积分思想
莱布尼茨在数学上的最突出贡献是他独立地创立了微积分，因此在微积分的创立上，莱布尼茨与牛顿分享荣誉．
莱布尼茨的微积分思想没有牛顿那样细腻，但逻辑程式却很清楚，这与他们各人的哲学思想有关．牛顿属于“英国经验主义者”，莱布尼茨属于“大陆理性主义者”．牛顿的流数概念及理论，充满着经验主义气息，莱布尼茨的微积分概念和算法程序，表现了逻辑发展的必然趋势．
莱布尼茨在巴黎时与荷兰数学家、物理学家惠更斯(C.Huygens)的结识交往引发了他对数学的兴趣，在惠更斯的帮助下，他学习了帕斯卡的一些数学著作，了解了那个时代数学的前沿知识，如不可分量，特征三角形等，他很快抓住了其中的本质东西，提炼出特征三角形两边商的极限的重要概念，并发现这些概念对于求切线与求面积的意义．
如图8-6所示，如果把AD看做是曲线BDC在C点的法线，而不仅仅是像帕斯卡认为的圆的半径，帕斯卡的方法就可以推广．这时只要对任意给定的曲线BDC，构造无穷小三角形EFD．过D作曲线的法线DA．DA就成了圆半径的作用．用D作横轴垂线DK．便得到两个三角形相似．
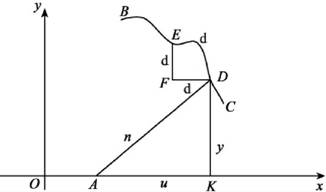
图8-6
△EFD∽△AKD，由此可得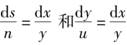
，即yds=ndx和udx=ydy对于这些无穷小量求和，得到
莱布尼茨称式(8-13)左边为“给定的曲线关于x轴的矩”，该矩等于以曲线的法线为纵坐标的曲线下的面积．若把这个“矩”乘以2π，所得的是曲线绕x轴旋转而成的旋转体的表面积．因此
A=2π∫yds=2π∫ndx
而式(8-14)中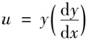
，所以经代替，得
公式(8-15)清楚地确定了切线问题
与求积问题计算(∫ydy)的互逆关系．
莱布尼茨还发现，适当地建立与特征三角形的相似关系可以进一步解决曲线的求长与求积问题．例如，t表示曲线的切线界于x轴与长度为a的垂线之间的一段长度．
由图8-7中两个相似三角形知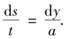
即ads=tdy，因此
∫ads=∫tdy
上式表明，曲线的求长问题可以化为一个求积问题——求处于y轴和另一条曲线之间的区域的面积．1673年是莱布尼茨微积分思想形成和发展的关键一年，除了上述一系列发现外，他还费了相当大的精力研究了切线这个互逆的问题．其中莱布尼茨在数学史上第一次
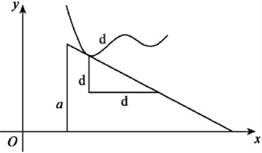
图8-7
明确地引入了函数的概念，还发现了泰勒级数．
1673年以后，莱布尼茨开始了他的微积分符号化进程，如用“∫”代替“omn”(求和)用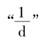
表示“ò”相反的运算的符号．即若．“ò”y=z，则
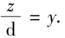不过，莱布尼茨很快发现将d放在分母上是不必要的．1673年11月11日，他毅然把作为积分逆运算的微分运算符号改成了“d”，这是很关键的一步．因为莱布尼茨的微积分，是以微分方法为中心内容的．不引出微分符号也就不可能实现微积分的解析比．
简单的微分法则，容易从积分法则中对应得到，例如
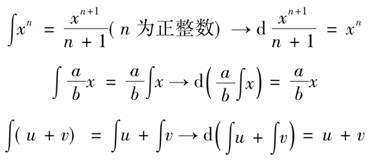
在探究积和商的微分法则时，莱布尼茨虽然通过具体例子的试算，否定了d(uv)=dudv和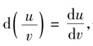
但没有及时找到正确公式，到1677年，他才得到
d(xy)=(x+dx)(y+dy)－xy=xdy+ydx+dxdy (8-16)
由dx和dy都是无穷小与xdy，ydx相比，dxdy更是无穷小，可以略去不计，得到
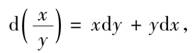
同样，在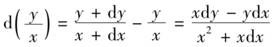
中，由于xdx与x2相比是无穷小，可以略去不计，所以得：
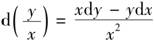，莱布尼茨一直采用∫和dx、dy来表示积分和微分，由于这些符号十分简明，逐渐流行于世界，沿用至今．
莱布尼茨深刻地认识到∫和d的互逆关系，这一思想的产生是莱布尼茨创立微积分的标志．实际上莱布尼茨的微积分理论就是以这个被称为微积分基本定理的重要结论为出发点的，在定积分中，这一定理直接导致了——莱布尼茨公式的发现．
综上所述，莱布尼茨已经建立起了一套相当系统的微分和积分方法．他成为牛顿同时代的另一位微积分发明者．
8.2.3 评说两种微积分
1.两种微积分的共同点
首先，牛顿和莱布尼茨两人都是经过一个世纪孕育的微积分的最后完成者．他们是各自独立地发现了微积分的基本定理．并建立了一套有意义的微分、积分算法．其次，他们都把微积分作为一种适用于一般的普遍方法．第三，他们都把微积分从几何形式中解脱出来，而在代数的概念上建立了微积分．而他们使用的代数记号和方法，不仅给他们提供了比几何更为有效的工具，而且还允许许多不同的几何和物理问题用同样的方法处理．第四，牛顿和莱布尼茨均把面积、体积及其他们以前作为和来处理的问题归并到反微分．因此四个主要问题——速率、切线、最值、求和——全部归结为微分和反微分．
2.两种微积分的主要差别
第一，牛顿和莱布尼茨两人微积分工作的起点不同．牛顿一开始就表现集大成者的姿态．在对前人工作进行分析综合的基础上，建立起一个概念明确，算法正确，应用有效，体系完美的理论．牛顿十分重视思想的合理性，一再修改作为他学说出发点的概念的逻辑基础．而莱布尼茨是在迅速发现和揭示微积分基本原理的基础上发展他的学说，他的天才表现在深刻的洞察力和有效的扩展上，而不是严密的表述和体系的逻辑完整性上．
第二，牛顿把x和y的无穷小增量作为求流数或导数的手段，当增量越来越小时，流数(或导数)实际上就是增量的比的极限，而莱布尼茨却直接用x和y的无穷小增量(即微分)求出它们之间的关系．这个差别分别反映了牛顿的物理方向和莱布尼茨的哲学方向．
第三，牛顿自由地用级数表示函数，而莱布尼茨宁愿用有限的形式．
第四，他们的工作方式不同．牛顿是经验的，具体的和谨慎的．而莱布尼茨是富有想象的，喜欢推广的，而且是大胆的．
第五，牛顿的变化率，即导数的概念作为其学说的核心，由此出发，通过逆过程来解决面积和体积问题．而莱布尼茨则把独立的微分dx和dy作为基本概念，面积和体积被设想成无穷多个微分之和，只在实际计算中才用反微分来求这些和．
另外，牛顿和莱布尼茨的微积分都缺乏清晰的、严谨的逻辑基础．这在初创时期，是不可避免的，直到19世纪，微积分学的逻辑基础才得以完善．
3.优先权之争
牛顿于1665～1666年创立了微积分．但是从来没有发表，只是把他的结果通知了他的朋友．莱布尼茨于1675年将他自己的微积分版本发表出来，以微分法则写了一篇论文．后又于1684年在莱比锡大学的新刊物《学术论文集》上，发表了他的完整的微分法．其后又发表了积分法．1687年，牛顿才出版了《自然哲学原理》．其中就有他的流数法．这一切看来都相安无事，没有产生敌对的行为．直到1708年，一位局外人，牛津大学教授基尔(John keill)在皇家学会会刊上发表了一篇讨论离心力的文章．文中基尔把微积分的首功记在牛顿名下．同时也提到莱布尼茨．但将《学术论文集》的那篇文章称为第二．
1711年，莱布尼茨得知此事后非常愤怒，写信要求皇家学会收回那种说法．英国和欧洲大陆之间的论战于是展开了．
这场争吵的重要性不在于谁胜谁负，而是使数学家分成两派，欧洲大陆的数学家，尤其是贝努利(家族)兄弟，支持莱布尼茨，而英国数学家捍卫牛顿，两派不和甚至尖锐地互相敌对．约翰·贝努利甚至嘲笑并猛烈攻击英国人．英国数学家当然是予以回击，尤其是牛顿，他当时是皇家学会主席，因而利用他的职务之便，以别人的名字刊登他的反驳．该事件的结果是英国的和欧洲大陆的数学家停止了思想交换，即使两人之一的莱布尼茨于1716年11月4日去世了，这场争论也没有平息．欧洲大陆的人士依然坚持莱布尼茨是第一位．而英国人也固执地忠于他们的大师．现代学者有充分证据证明，这两位数学家的工作是相互独立的，而且从我们前面所作的比较可以看出，他们俩人在微积分上所作的工作可以称得上是相辅相成、珠联璧合．而且俩人的工作又各有特色．牛顿注意物理方面，而莱布尼茨侧重于几何方面．牛顿先于莱布尼茨发明了微积分，而莱布尼茨先于牛顿发表了微积分．尤其是莱布尼茨是花费了一生的努力，并咨询过许多数学家，为各种数学运算找到最佳记法，且在最后，数学家采用了莱布尼茨的微积分记法．
值得补充的是，尽管发生了纠纷，两位学者却从未怀疑过对方的科学才能．有一则记载说，1701年在柏林王宫的一次宴会上，当普鲁士王问到对牛顿的评价时，莱布尼茨回答道：“综观有史以来的全部数学，牛顿做了一半多的工作．”
优先权争论被认为是“科学史上最不幸的一章．”
从长远看，英国人输了．因为他们无法走出牛顿的阴影，不能取得新的数学突破．在其后的200年间，数学的成就中心是在欧洲大陆．