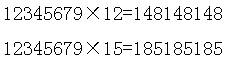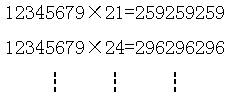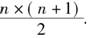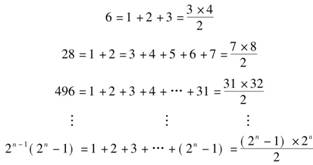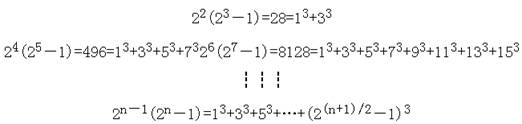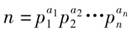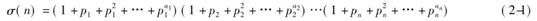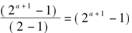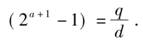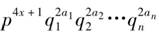§2.2 数字美学欣赏

数字中许多颇具魅力、令人叹赏的性质，使许多科学家、文学家、艺术家们大为感慨，伽利略曾说：“数学是上帝用来书写宇宙的文字．”毕达哥拉斯学派的学者，对于数字的崇拜达到“神话”的程度，他们崇拜“4”，因为它代表四种元素：火，水，气，土；他们把“10”看成是“圣数”，因为10是由前四个自然数1，2，3，4结合而成；他们还认为：“1”表示理性，因为理性是不变的；“2”表示意见；“4”代表公平，因为它是第一个平方数；“5”代表婚姻，因为它是第一个阴数2与第一个阳数3的结合．近年来，人们喜欢数字8，是因为它意味着“发”，也有人喜欢“6”，因为那意味着“六六大顺”．人们不惜出高价抢注末尾是“8”或“6”的汽车牌号、移动电话号码等．可见，数字中蕴涵着丰富的文化．不过，这只是一些表面现象，深入一点研究它们的性质，人们会为数字王国的奇妙而赞叹不已．

2.2.1 亲和数(也叫相亲数)

远古时代，人类的一些部落把220和284两个数字奉若神明，男女青年结缔婚姻时，往往把这两个数字分别写在不同的签上，两个青年在抽签时，若分别抽到了220和284，便被确定为终生伴侣；若抽不到这两个数，他们则天生无缘，只好分道扬镳了．这种缔婚方式固然是这些部落的风俗，但在某些迷信色彩的背后，倒也有些说道．表面上，这两个数字似乎没有什么神秘之处，然而，它们却存在着某些内在的联系：

能够整除220的全部正整数(不包括220)之和恰好等于284；而能够整除284的全部正整数(不包括284)之和又恰好等于220．

这真是绝妙的吻合！

也许有人认为，这样的“吻合”极其偶然，抹去迷信的色彩，很难有什么规律蕴涵于其中，恰恰相反，这偶然的“吻合”引起了数学家们极大的关注，他们花费了大量的精力进行研究、探索，终于发现“相亲”数对不是惟一的．它们在自然数中构成了一个独特的数系．人们称具有这种性质的两个数为亲和数(或相亲数对)．

第一对相亲数(220，284)也是最小的一对，是数学先师毕达哥拉斯发现的

1+2+4+5+10+11+20+22+44+55+110=284

1+2+4+71+142=220

这一性质，引起了毕达哥拉斯的极大兴趣，他们把这两个数比做一对亲密的恋人，称它们是亲和数．是否还有别的亲和数呢？两千多年后：

第二对相亲数(17296，18416)于1636年由法国天才数学家费尔马找到了；

第三对相亲数(9363548，9437056)于1638年被法国数学家笛卡儿发现；

1750年，瑞士伟大的数学家欧拉一个人就找到了60对相亲数对，并将其列成表，(2620，2924)是其中最小的一对．当时，人们有一种错觉，以为经过像欧拉这样的大数学家研究过，而且一下子找到60对亲和数，在比该表中所找到亲和数小的正整数中不会再有亲和数了．然而，偏偏出人意料，有一对比该表中所列亲和数更小的亲和数，竟在大数学家的眼皮下溜过去了．100多年后，意大利16岁的少年巴格尼于1860年找到了一对比欧拉的亲和数表所列的数更小的亲和数对(1184，1210)，于是，这个本来已经降温的问题又重新引起了人们的兴趣．在比欧拉的亲和数表中所得的数更小的自然数中是否还有亲和数，到1903年有人证明了最小的五对亲和数是：

220和284，1184和1210，2620和2924，5020和5564，6232和6368

其中，第一对为毕达哥拉斯发现，第二对为意大利少年发现．其余三对则是欧拉的亲和数表中最小的三对．

今天亲和数的研究仍在继续，主要有两方面的工作：

(1)寻找新的亲和数；

(2)寻找亲和数的表达公式．

迄今为止，人们已经找到了1200对“亲和数”，亲和数要么两个都是偶数，要么两个都是奇数，是否存在一奇一偶的亲和数呢？这个问题是欧拉提出来的，300多年来尚未解决．人们估计这是一个像哥德巴赫猜想那样困难的问题．

到1974年为止，人们所知的一对最大的亲和数是：

3⁴·5·5 281¹⁹·29·89·(2·1291·5281¹⁹－1)

3⁴·5·11·5281¹⁹(2³·3³·5²·1291·5281¹⁹－1)

以这两个数字的偶然性竟然引出了数论中一个丰富的数系，这确实令人惊叹不已．

最近，人们把亲和数对推广成亲和数链．链中每一个数的因数之和等于下一个数，而最后一个数的因数之和等于第一个数，比如：2115324，3317740，3649556，2797612等．

还有学者把亲和数推广到“金兰数”，即数组中第一个数的所有真因数之和等于第二个数与第三个数之和；而第二个数的所有真因数之和等于第一个数与第三个数之和；而第三个数的所有真因数之和等于第一个数与第二个数之和．简而言之，每个数的真因数之和都等于另两个数之和．例如：1945330728960；2324196638720；2615631953920．

目前所知最小的金兰数是：123228768，103340640，124015008．

2.2.2 完全数(完美数)

与亲和数类似具有奇妙的特征和神秘意义的数是完全数．在古希腊，毕氏学派在一些数字中，看到一完美的性质；这些数小于或等于它的所有因数(即真因数)之和．它们称这种数为完全数．如6，小于6的正因数有1，2，3，而6=1+2+3.6也确实与宗教里面的一些完美性相关联，在西方圣经里记载，上帝在6天内创造世界，因此，古代人认为6是一个很完美的数字；28是第二个完全数．28=1+2+4+7+14．

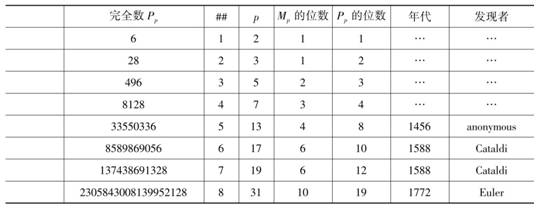
随后，496=1+2+4+8+16+31+62+124+248；可见496是完全数．类似地，第四个具有这种性质的数是8128，这个数是早在1800多年前就为人所知．看来，完全数不多．前8000多个正整数中才4个．物以稀为贵，完全数稀罕．

完全数即完美数，人们用美来形容完全数，表明这种数的完美．一方面表现在这种数稀罕，奇妙；一方面表现在这种数的完满．各因数之和不多不少等于这种数自己，第5个完美数在哪里？在距离发现第四个完美数之后一千多年，于公元1538年终于发现了第5个完美数33550336.又过了50年才发现第6个完美数8589869056．

寻找这种数那么难，却还有人去寻找，到现在为止，也只发现了二十多个．

欧几里得发现，前四个完美数皆可以表示为2^n－1(2ⁿ－1)的形式．当n分别为2，3，5，7时

n=2，2¹(2²－1)=2×3=6

n=3，2²(2³－1)=4×7=28

n=5，2⁴(2⁵－1)=16×31=496

n=7，2⁶(2⁷－1)=64×127=8128

欧几里得也看出，当n=2，3，5，7时，2ⁿ－1是素数．这项观察使得他在《几何原本》里证明了下述结论：

若2ⁿ－1为素数，则2^n－1(2ⁿ－1)为一完全数．同时，我们还有下述结论：

对每一个正整数n，若2ⁿ－1为素数，则n为素数．

找完全数不是一件易事．17世纪法国数学家笛卡儿(R.Descartes)曾预言：能找出的完全数不会太多的，好比要在人类中找到完人(Perfect man)一样，亦非易事．

2.2.3 梅森数与梅森素数

因为，形如2ⁿ－1的素数与完美数有十分密切的关系．只要确定了2ⁿ－1是素数，就很容易确定相应的完美数．

形如2ⁿ－1的素数，最早以笛卡儿的好朋友，法国神父梅森最有兴趣，故后来对一素数P，便称MP=2^P－1为梅森数．且当M_P为素数时，称该数为梅森素数．

例如：M₂=2²－1=3；M₃=2³－1=7；M₄=2⁴－1=15；M₅=2⁵－1=31

梅森本人1644年在他的著作《物理—数学探索》的序中猜想，在不超过257的55个素数中，仅当P=2，3，5，7，11，13，17，19，31，67，127，257时，2^P－1为素数；而P＜257的其他素数对应的M_P都是合数．梅森是如何得到这一结论的呢？无人知晓，他本人验证了前7个数都是素数，后4个数因计算量太大未能验证．1772年，欧拉证明了第8个2³¹－1是素数； 1877年，吕卡又进一步证明了第10个2¹²⁷－1也是素数．夹在中间的第9个2⁶⁷－1是不是素数呢？自然引起了人们的关注．近200年来，不断地有学者在研究这个问题．除了已提到的12个数外，另外还有16个形如2^P－1的梅森素数，其中

P=521，607，1279，2203，2281，3217，4253，4423，9689，

9941，11213，19937，21701，23209，44497，86243

第28个梅森素数2⁸⁶²⁴³－1也是一个非常大的数．这个数字写出来共有两万五千多位．仅写下来这个数就要花几个小时，用二三十页纸．至于要判断这个数是否为素数，那就难上加难了．只要试试判断P=641，811，977这样的3位数时2^P－1是否为素数，就能体会到有一定的难度，更不要说对十位数，百位数判断是否为素数时的难度．

1947年，有了台式计算机后，人们检查到梅森猜想的五个错误，M₆₇，M₂₅₇不是素数．而M₆₁，M₈₉，M₁₀₇是素数．

1903年10月，在美国纽约召开的一次学术会议上，美国数学家科尔提交了一篇论文《大数的因子分解》．轮到科尔报告时，他一言不发，只在黑板上写下两行字：

2⁶⁷－1=147573 952 589 676 412 927

19370721×761838257287=147573 952 589 676 412 927

两个数计算结果完全一样．之后，他只字未吐又回到自己的座位上．时间不过一分钟．顿时台下爆发了热烈的掌声．人们欢呼200多年的一个难题终于解决了！原来科尔证明了2⁶⁷－1不是素数，2⁶⁷－1有两个在黑板上写出来的因数．这个“无声的报告”已经成为数学史上的佳话．

电子计算机的出现，给人们验算和寻找梅森素数带来了方便．

1971年3月4日晚上，美国国家电视台中断了正常的节目播放，而发表布鲁思特·托克曼用电子计算机找到P=19937时，2^P－1是素数的消息(这个数有6987位)．同年，美国人斯可洛温斯基找到了更大的梅森素数P=44497时(这个数有13395位)，2^P－1是素数．

1983年1月，这位美国人在CRAY－1型计算机上发现P=89243时(这个数有25962位)，2^P－1是素数．接下来的纪录是1983年末，发现P=132049时(这个数有39751位)、1985年发现P=216091时(这个数有65050位)、1992年3月发现P=859433时(这个数有258716位)、1996年9月发现P=1257787时(这个数有378632位)，2^P－1是素数．其中最后一个也是迄今为止，人们发现的最大素数．

梅森数的研究具有广泛的应用，如在代数编码等应用学科中的应用．但长期以来，对这种素数的研究并非由应用而推动的，而是出于人们对于整数的许多性质的研究，出于对自然美的欣赏与追求，人类的智慧光芒也在其中闪烁．人类也在这种追求中显示出自己的价值．

2.2.4 回文数与回文素数

“回文”是我国古典文学作品中的一种特殊体裁，有回文诗，回文联等．回文的特点是：在一篇作品中，作者精心挑选字词，巧妙地安排顺序，使得一篇作品倒转过来从头读起，也同样是有意义的作品．

虽然，大多数回文作品都是意义不大的文字游戏，但唐宋以来，确实也有不少写得好的回文，宋人李愚写的一首思念妻子的回文诗：

枯眼望遥山隔水，往来曾见几心知．

壶空怕酌一杯酒，笔下难成和韵诗．

途路阻人离别久，讯音无雁寄回迟．

孤灯夜守长寥寂，夫忆妻兮父忆儿．

将这首诗倒过来读，就变成：

儿忆父兮妻忆夫，寂寥长守夜灯孤．

迟回寄雁无音讯，久别离人阻路途．

诗韵和成难下笔，酒杯一酌怕空壶．

知心几见曾来往，水隔山遥望眼枯．

这首诗的绝妙之处是，顺诗时是“夫忆妻兮父忆儿”，倒过来读时，成了“儿忆父兮妻忆夫”．既可以看成丈夫思念妻子的诗，也可以当做妻子思念丈夫的诗．简直可以称为夫妻互忆回文诗了．

在市场经济的今天，有些商家广告、对联也使用回文，招引顾客，如北京的一家酒店，店名叫“天然居”．店里有一副对联：

客上天然居，居然天上客．

顾客走进这家酒店，看了这副对联，想到自己居然是天上的来客，在没有得到物质享受之前，就已经得到充分的精神享受了．

有趣的是，在数学中也有“回文数”，“回文素数”．

任取一个自然数，如3001，将这个数各位数字倒过来，就得到一个新的自然数1003，称为原数的反序数．如果一个数与这个数的反序数相等，就称这个数为回文数．如2002，3003，434等．

对于回文数，比较容易找到．甚至从一个不是回文数的二位数可以用下面的方法得到回文数，即：任取一个二位数，如果这个数不是回文数，则加上这个数的反序数．如果其和仍不是回文数，就重复上述步骤，经过有限次这样的加法运算后，一定能够得到一个回文数．

例如，给一个数97，这个数不是回文数，加上反序数79，97+79=176，176还不是回文数，再将上述运算过程继续下去，将176加上反序数671，176+671=847，将847+748= 1595，如此继续下去，便逐步得到：

1595+5951=7546，7546+6457=14003，14003+30041=44044，44044即为回文数．

对于有些三位数，如197，用上述方法：197+791=988，988+889=1877，1877+7781= 9658，9658+8569=171017，171017+710171=881188也可以得到一个回文数881188．

只是这种构成回文数的方法是否普遍适用，目前尚未能证明．也未能否定．据说这将是一个世界难题．不过上述方法已经足够找到充分的回文数了．而对于寻找一个回文素数，恐怕就要困难得多．所谓回文素数，即一个数，与其反序数均为素数，如17和71，113和311，347和743，769和967等都是回文素数．人们以像作诗的兴趣那样去计算和研究回文素数，2位数的回文素数有4对，3位数的回文素数有13对；4位数的回文素数有102对；5位数的回文素数有684对．但究竟有多少对这样的回文素数？至今仍是未揭开的谜．

314159是一个素数，其反序数951413也是一个素数，人们浮想联翩，竟发现π的前六位数字是一个回文素数．且容易看到，π的前两位数字31也是一个回文素数，π是一个无限循环小数，其各位数字似乎是毫无规律的．可是人们发现了这个数许多奇妙而有趣的性质，这仅是一例．19世纪下半叶，不仅证明了π是无理数，而且还证明了这个数不是代数无理数．即证明了这个数是超越数．这里顺便说一句，关于π，还可注意到这样一个有趣的事实：这个数的小数点后的前三位数字141的和1+4+1=6是第一个完美数．前七位数字1415926的和1+4+1+5+9+2+6=28恰好是第二个完美数，真是不可思议．

关于π还有许多其他的有趣的事实将在后文叙述．

俗话说，作回文诗难，找回文素数难上加难．不过，再难的事也有人做．那是因为它的奇妙所吸引．比如：人们还发现了五位，六位循环回文素数，如图2-1、图2-2所示．

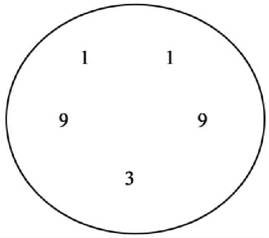
图2-1

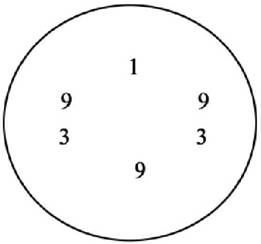
图2-2

从其中任一数字开头，都能得到一回文素数．

此外，人们还构造N×N的矩阵，使其行、列和主对角线上的数字组成的数均为回文素数(这类回文素数共有4(N+1)个)．比如下面4×4，5×5数阵即是其中之一

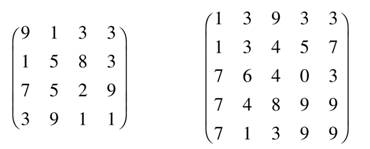
有兴趣的读者可以试一试．

2.2.5 素数定理及孪生素数定理

首先，关于素数有两个有趣的问题．

第一个问题是：素数有多少个？结论是素数有无限多个．欧几里得用反证法证明了这个结论：其证法是假定素数只有有限个．将它们罗列如下：

P₁=2，P₂=3，…，P_n

那么数P₁P₂…P_n+1将不为上述素数中任一个所整除，因此，或者这个数本身是一个素数，或者这个数有不同于上述素数的新的素数因子．这与假设矛盾．结论得证．

关于素数无限的证明是数学证明中的一个典范．如果世界上确实有经典性的伟大定理，那么欧几里得的证明就是一例．实际上，他的论证常常被人们作为数学定理的典范．因为这个定理简洁，优美，又极为深刻．

第二个问题是：相邻素数的间距有多大？结论是：相邻素数的间距要多大就有多大．举例证明如下：

存在999个连续的自然数，其中没有一个是素数，它们是

1000！+2，1000！+3，…，1000！+1000

易见，第一个数能被2整除，第二个数能被3整除，……，最后一个数能够被1000整除．这就造出了999个连续的自然数，其中没有一个是素数．用类似的方法可以造出更大的间隔．这就完成了结论的证明．

今问有多少对相差为1的素数？很清楚，2是惟一的偶素数．其他的素数都是奇素数．它们的差是偶数．这样一来，2与3是惟一的一对相差为1的素数．同样地，2与5是惟一的一对相差为3的素数．2与7是惟一的一对相差为5的素数．不存在相差为7的一对素数．

相差为2的素数怎样呢？显然，这样的素数必然都是奇数．这种素数对叫做孪生素数，如3，5；5，7；11，13；17，19；29，31它们像“孪生兄弟”一样．孪生素数在数的群体之中，就像孪生兄弟在人的群体中特别被人关注一样．孪生素数对的个数是有限的，还是无限的？这个问题仍然没有答案．半个世纪以来，这个问题已经成为数论中最高深的研究课题之一．

我们还可以看到几对孪生素数

41，43；59，61；71，73；101，103；107，109；137，139；…

更大的4位数的孪生素数，如：3389，3391；4867，4969

找出10位数以上的孪生素数就十分不容易了，如：

99 999 999 959，99 999 999 961；10 00 000 009 649，1000 000 009 651

20世纪70年代末发现了更大的孪生数：297×2⁵⁴⁶－1，297×2⁵⁴⁶+1．

随之又发现：1159142985×2²³⁰⁴－1，1159142985×2²³⁰⁴+1．

已经知道，十万以内的孪生素数有一千多对，一亿以内的孪生素数有十万对以上．

与“孪生素数”问题有关联的问题是：在等差数列中寻找素数的问题．

算术数列又称为等差数列，这是一个从第二项起每项与其前面一项的差均为常数(称为公差)的数列．

算术数列有许多性质，然而其中的所谓算术素数列就鲜为人知了．所谓算术素数列是指各项均为素数的算术数列．

尽管早在1837年，狄里赫莱(Dirichlet，1805～1859)就已证明：首项为a，公差为d的算术数列中，若(a，d)=1，即a与d互素，则这个算术数列中有无穷多个素数．

1944年，学者们又证明了：存在无穷多组由三个素数(不一定相继)组成的算术素数列．但是，要寻找全部由素数组成的算术数列，却远非那么容易．

可以证明，由n个素数组成的算术数列，其公差必须能被小于n或等于n的全部素数整除，这样，数列的首项与公差必须很大．

20世纪70年代，学者们找到了项数是10的算术数列；其首项是199，公差是210，它们是：

199，409，619，829，1039，1249，1459，1669，1879，2089

1977年发现了有17项的算术素数列．

1978年，美国的Pritchard利用电子计算机花了近一个月的时间(每天工作10小时)，找到了有18项的算术素数列．

该数列的首项是10792827，末项是2766 1858 7107，公差是99 22 78 2870．

1984年还是Pritchard这位康奈尔大学的教授，又找到了项数为19的算术素数列．其首项是829 7644 387，公差是418 0566 390．

2.2.6 涉及素数的问题

我们知道，素数是数论的主要中心对象，虽然100多年前素数定理得到证明后，素数理论有了不少进步，但仍有许多问题有待解决．

1.是否存在大于2的偶数，不是两个素数的和？

2.是否存在大于2的偶数，不是两个素数的差？

3.是否存在无穷多对孪生素数？

4.是否存在无穷多个梅森素数？

5.是否存在无穷多个梅森素数是复合数？

6.是否存在无穷多个费尔马素数(即2²ⁿ+1型的素数)？

7.是否存在无穷多个费尔马素数是复合数？

8.是否存在无穷多个素数具有xⁿ+1的形式？其中x是整数．

9.是否存在无穷多个素数具有xⁿ+k的形式？其中k是给定的数．

10.对于每一个整数n≥1，是否在n²与(n+1)²之间至少存在一个素数？

11.对于每一个整数n＞1，是否在n²与n²+n之间至少存在一个素数？

12.是否有无穷多个素数，其中每一位都是1(如11和11 111 111 111 111 111 111 111)？

上述的每一个问题都简要清晰，但是解决这些问题是极其困难的．

2.2.7 数字趣谈

1.神奇的“无8数”

在数学王国里，有一位神奇的主人，它是由1、2、3、4、5、6、7、9八个数字组成的一个八位数——12345679．因为这个数没有数字“8”，所以，我们都管这个数叫“无8数”．

“无8数”虽然是由普通的八个数字组成的，但是这个数具有许多奇特的功能．这个数与几组性质相同的数相乘，会产生意想不到的结果．

这个数若是与9、18、27、36、45、54、63、72、81(9的倍数)相乘，结果会由清一色的数字组成，即

“无8数”不仅能乘出清一色的积，而且还能与12，15，21，24，…(3的倍数，其中9的倍数除外)相乘，得出由3个数字组成的“三位一体”这种特殊的结果

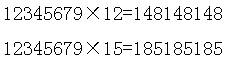
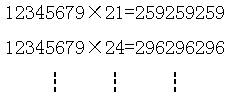
这个数若是与10、11、13、14、16、17相乘，乘得的积会让8、7、5、4、2、1轮流休息(3、6、9是3的倍数，就轮不到它们休息了)．

看了这个结果后，读者一定会说：“无8数，真奇妙！”然而，这类数与10、19、28、37、46、55、64、73相乘，积会让1、2、3、4、5、6、7、9八个数字轮流做首位数．

这个神奇的“无8数”与循环小数有关．请看

这个“无8数”还有不少有趣的性质，随着人们对“无8数”研究的深入，这种有趣的性质会越来越多地被发现．

只要我们多学习，多积累，就一定能探索出更多的奥秘．

2.美的组合

有一些数字，往往要通过计算，通过不同数字的组合，才可以得到一些非常奇妙的排列，令人看后叫绝，回味无穷．

这里的“·”，是乘号的意思，以下都是如此．

3.续谈完全(美)数

完全数是非常奇特的数，这类数有一些特殊性质，例如每个完全数都是三角形数，即都能写成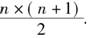．即

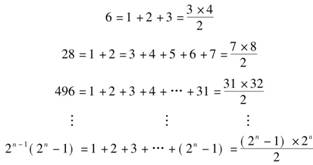
把这类数(6除外)的各位数字相加，直到变成一位数，那么这个一位数一定是1；这类数都是连续奇数的立方和(6除外)：

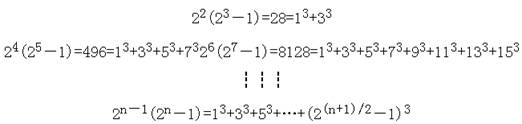除了因子1之外，每个完全数的所有因子(包括自身)的倒数和等于1，比如

完全数都是以6或8结尾的，如果以8结尾，那么就肯定是以28结尾，再看看它们的二进制表达式

数论里有一个著名的函数σ(n)，表示自然数n的所有因子之和，包括因子n本身在内．于是利用σ(n)，完全数可以定义为使得σ(n)=2n的数.我们来推导一下完全数的表达式．

假设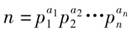是n的标准素因子分解式.则n的所有因子之和是如下式子的乘积

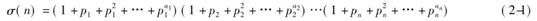
而这个乘积就是如下式子

设偶完全数n=2^aq，这里q表示奇素数乘幂之积.设s是q的一切除数之和，也包括q本身在内，而d只是表示它的真除数之和，所以s=q+d，由公式(2-2)知道，2^a的一切除数之和为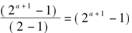.因此n的全部除数之和等于s(2^a+1－1)，而由完全数的定义，知道这个和数应该等于2n，即有：2n=2^a+1q=s(2^a+1－1)=(q+d)(2^a+1－1)；化简得

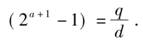
这意味着d是q的一个真除数，但是前面又知道d是q的一切真除数之和，因而d只能是q的惟一的真除数，于是d的惟一可能值是1，而若一个数的真除数之和为1，则该数必然是一个素数，所以q=(2^a+1－1)是一个素数，最后得到n=2^aq=2^a(2^a+1－1).这就是偶完全数的表达式，即公式(2-1)．

注意以上谈到的完全数都是偶完全数，至今仍然不知道有没有奇完全数，如果真的存在奇完全数，那么必须满足如下这些条件：

(1)N必须是一个形如12n+1，或9(4k+1)的数.

(2)N至少要有6个不同的素数因子.

(3)N必须具有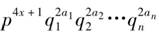的形式，这里p=4k+1

上述第(3)条中还要限制为：如果除了第一个以外，所有的a等于1，则a₁不能等于2；除了第一个，第二个以外所有的a都等于1，则前面两个a₁，a₂不能等于2.

如果所有的a都等于2，则N不可能是完全数.

若所有的q的指数都递增1，则由此得出的指数不能有9，15，21或33作为公共除数．

若p的指数4x+1等于5，则所有的a都不能等于1或2．

若N不能被3整除，则它至少要有9个不同的素数因子；若N不能被21整除，则N至少要有11个不同的素数除数；若N不能被15整除，则N至少要有14个不同的素数除数；若N不能被105整除，则N至少要有27个这样的除数，这就要求N至少大于10⁴⁴．

若N正好有r个不同的素数除数，则最小的一个应该小于r+1．例如若N(假设N存在)有28个不同的素数除数，则最小的一个不应大于29．

已经有学者证明如果N存在，将大于10¹⁰⁰．

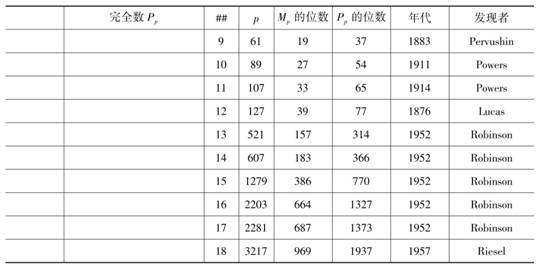
表2-1列出了前18个完全数．

表2-1

续表